一类企业竞争模型的动力学分析

劳红月，葛立茜，张茂云，孙 梦，陈子晗，李 锋

（临沂大学 数学与统计学院，山东 临沂 276005）

一类企业竞争模型的动力学分析

劳红月，葛立茜，张茂云，孙 梦，陈子晗，李 锋

（临沂大学 数学与统计学院，山东 临沂 276005）

建立了具有产出水平下临界点的企业竞争型模型，研究了该系统的平衡点的存在性及稳定性，并通过数值模拟的方法验证了研究结果，最后给出了模型的理论解释。

竞争模型；平衡点；稳定性

1 研究背景

经过20多年的飞速发展，中国经济逐渐进入调整阶段，市场竞争激烈而又紊乱。在市场经济条件下，各类企业为取得较好的产销条件、获得更多的市场资源而不断竞争，从原来简单的规模、实力、活力竞争逐阶上升到核心力的竞争。通过竞争，既实现了企业的优胜劣汰，又实现了生产要素的优化配置，提高了国家的核心竞争力。在竞争性市场条件下，各个企业除了通过培育自身资源和能力，还通过竞争获取外部可利用资源，在为顾客创造价值的基础上，实现自身价值的综合性能力。在竞争性的市场中，一个企业所具有的能够比其他企业更有效地向市场提供产品和服务并获得赢利和自身发展的综合素质的能力，是现代企业成功的关键。

众所周知，生物体研究的本质与经济社会企业研究的本质具有相似性。特别地，企业间的竞争与合作关系与生物物种种群间的关系更有诸多类似之处，利用生态模型研究企业间的竞争关系已经引起了众多学者的关注。文献[1]提出具有下临界的企业竞争模型，并以2个企业之间的竞争为例，运用微分方程定性知识以及数值仿真，对该模型所表达出来的几种企业竞争情况及其稳定条件进行了系统分析。文献[2]引入生物物种的Lotka-Volterra（LV）种间竞争模型，建立了单一电子商务平台企业、双电子商务平台企业及多个电子商务平台企业的LV竞争模型。

文献[3]中指出：自然界中有一条“正反馈循环”规律，即一件事情的发生、发展受到了另一件事情的刺激，从而促进了其正向发展。比尔·盖茨在《未来之路》中也提出了类似的“正螺旋效应”，这都与生态系统中种群竞争的一种模型具有相似性，即“好的越好，而糟的越糟”，导致“赢家通吃”。目前，企业之间也存在这种正反馈效应，导致诸多中小企业在竞争中处于劣势地位，在与大企业相互竞争过程中被兼并或者破产。然而，2个实力相当的企业在竞争过程中其企业实力又是如何变化的呢？

已有不少学者将LV模型应用于经济问题的研究中，但大部分都只是研究宏观问题，对于微观问题的研究很少涉及。文献[4]根据企业集群与生物种群的相似性，建立了网状型企业集群模式下企业间竞争关系的数学模型。

本文主要考虑2个企业间的竞争，用x, y表示企业的产出水平，其为时间t的函数； a, b为竞争系数；N表示最大市场容纳量。这里假设2个企业实力相当，且内禀增长率相同，2个企业的最大容纳量也相同。考虑到实际情形，引入企业产出水平的下临界点L，表示企业产出水平的最低限度。在企业产出水平低于此限度时，企业生产成本将高于收益，因亏损而导致企业破产。这比现有文献所建立的企业竞争生态模型更符合现实。

下面引入LV模型来描述这种竞争关系。假设有其他企业竞争的条件下，当一个企业规模超越另一个企业时，会对另一个企业的发展起到反作用。综上所述，在LV种间竞争模型改进和扩展的基础上建立如下企业竞争系统：

式中r为企业自身增长率。

下面主要利用微分方程定性理论[5]，并借助Maple软件，研究系统（1）的平衡点及其分类，进而得到系统存在多稳的条件。

2 系统平衡点分析

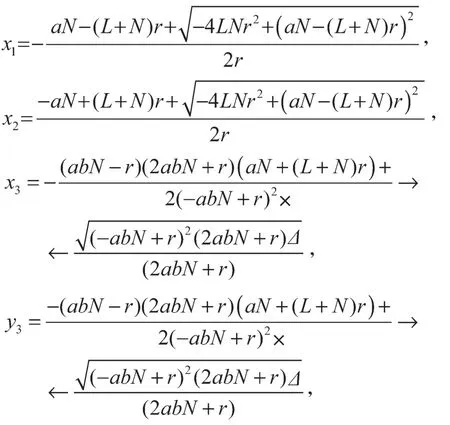
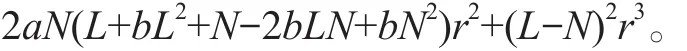
通过对上述9个平衡点进行分析，可得定理1。

系统（1）有9个平衡点O(0, 0)，A1(L, 0)，A2(0, L)，A3(N, 0)，A4(0, N)，A5(x1, x1)，A6(x2, x2)，A7(x3, y3)，A8(y3, x3)；

定理1证明从略。

通过详细计算可得定理2～5。

定理2 O(0, 0)是系统的稳定结点。

证明 系统在O(0, 0)的线性化矩阵为

因此系统有二重特征根，从而O(0, 0)是系统的稳定结点。

定理3 A1(L, 0)，A2(0, L )是系统的鞍点。

证明 系统在A1(L, 0)，A2(0, L)的线性化矩阵分别为

从而系统有2个异号的特征根，A1(L, 0)，A2(0, L)是系统的鞍点。

定理4 A3(N, 0)，A4(0, N)是系统的稳定结点。

证明 系统在A3(N, 0)，A4(0, N)的线性化矩阵分别为

从而系统有2个负的特征根，A3(N, 0)，A4(0, N)是系统的稳定结点。

定理5 A7(x3, y3)，A8(y3, x3)是系统的鞍点。

证明 对于奇点A7(x3, y3)，A8(y3, x3)，通过复杂的运算可得

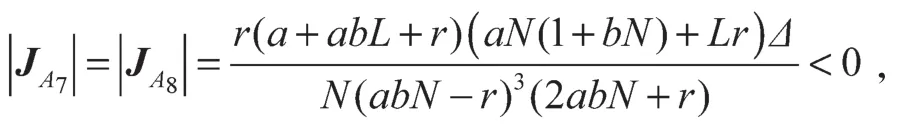
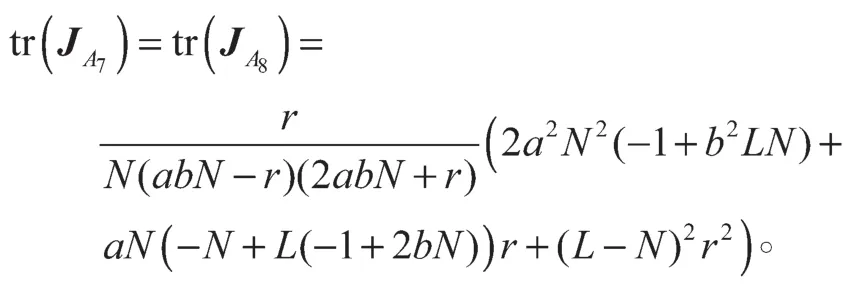
从而系统有2个异号的特征根，A7(x3, y3)，A8(y3,x3)是系统的鞍点。

对于奇点A5(x1, x1)，A6(x2, x2)，通过复杂的运算可得

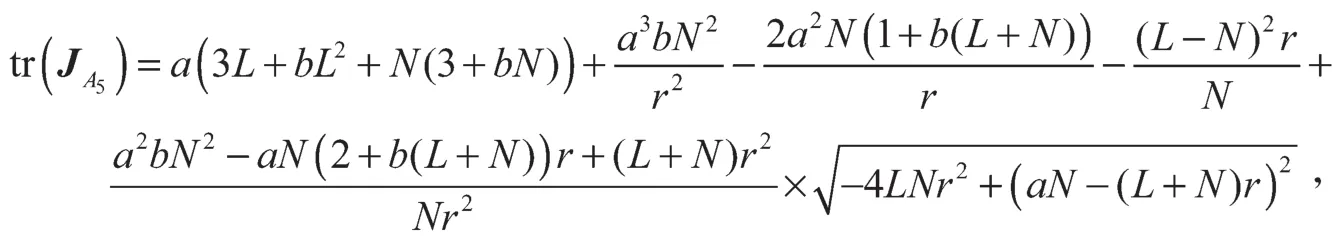
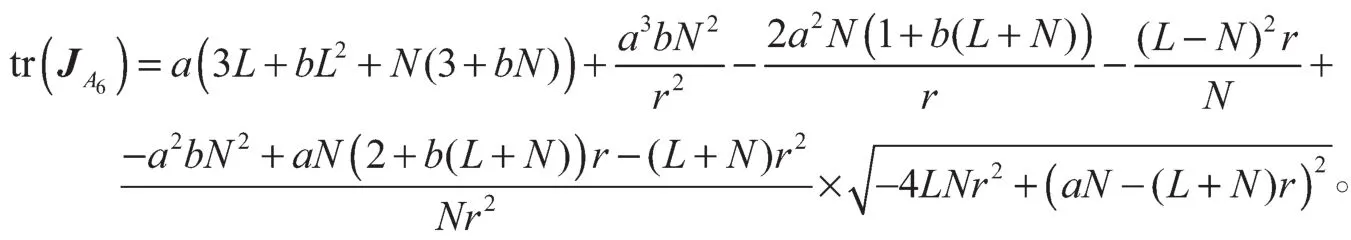
由于讨论过程复杂，不对A5(x1, x1)，A6(x2, x2)平衡点的类型进行详细讨论，而通过数值模拟研究其多稳现象。

3 数值模拟

因此，当r＞3.934 9时，系统有9个平衡点。例如当r = 4时，9个平衡点为(0, 0)，(0, 0.5)，(0.5, 0)，(0, 1)，(1, 0)，(0.625, 0.625)，(0.8, 0.8)，(0.760 483, 0.826 419)，(0.826 419, 0.760 483)。

经过分析可以得知，点(0.625, 0.625)是不稳定的结点，点(0.8, 0.8)是稳定的结点，这两点邻域的结构分别如图1和图2所示；系统在第一象限的结构如图3所示。

图1 (0.625, 0.625)邻域轨线Fig. 1 Trajectory in the neighborhood of (0.625, 0.625)

图2 (0.8, 0.8)邻域轨线Fig. 2 Trajectory in the neighborhood of (0.8, 0.8)

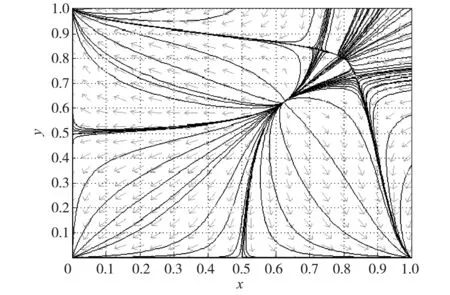
图3 系统第一象限相图Fig. 3 Phase diagram of the fi rst quadrant of the system

利用Maple软件，分析系统的无穷远奇点后，可得系统的poincare圆盘如图4所示。

图4 r=4时系统的poincare圆盘Fig. 4 Poincare disc of the system when r=4

所以系统在第一象限不存在周期解。

当3.497 06＜r＜3.934 90时，系统有7个平衡点。例如当r=3.9时，7个平衡点为：(0, 0)，(0, 0.5)，(0.5, 0)，(0, 1)，(1, 0)，(0.640 901, 0.640 901)，(0.780 151, 0.780 151)。

利用Maple软件，分析系统的无穷远奇点后，可得系统的poincare圆盘如图5所示。

图5 r=3.9时系统的poincare圆盘Fig. 5 Poincare disc of the system when r=3.9

当r＜3.497 06时，系统有5个平衡点。例如当r=3.4时，5个平衡点为：(0, 0)，(0, 0.5)，(0.5, 0)，(0,1)，(1, 0)。

利用Maple程序，分析系统的无穷远奇点后，可得系统的poincare圆盘如图6所示。

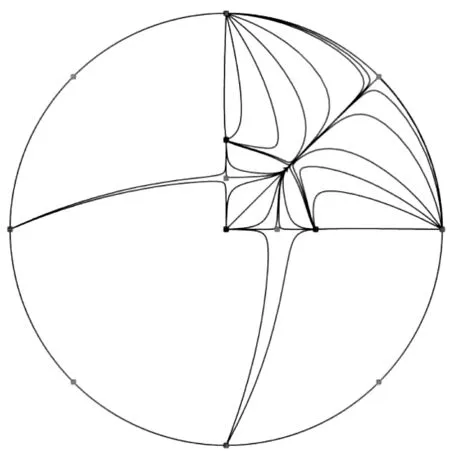
图6 r=3.4时系统的poincare圆盘Fig. 6 Poincare disc of the system when r=3.4

4 结论分析

本文建立了具有产出水平下临界点的企业竞争型模型，以两个企业之间的竞争为例分析得到了2个企业竞争时可能出现的几种情况及稳定条件：

稳定点的正平衡点是2个企业能够稳定共存的条件，也就是模型的稳定条件。通过数值模拟，能够得到2个企业可以稳定共存的条件。

[1] 张 睿，钱省三，高 臻. 基于生态学理论的企业竞争模型[J]. 系统工程，2008：26(2)：116-119.ZHANG Rui，QIAN Xingsan，GAO Zhen. A Competitive Model of Enterprises Based on Ecology Theory[J]. Systems Engineering，2008：26(2)：116-119.

[2] 叶琼伟，强 欣，宋光兴. 电子商务平台间LV竞争模型研究及其解释[J]. 商业研究，2014(6)：37-41.YE Qiongwei，QIANG Xin，SONG Guangxing.Research on LV Competition Model Between E-Commerce Platforms and Their Interpretation[J].Commercial Research，2014(6)：37-41.

[3] 周 星，克居正. 男生追女生的数学模型[J]. 数学的实践与认识，2012，42(12)：1-8.ZHOU Xing，KE Juzheng. The Boy-After-Girl Mathematical Model[J]. Mathematics in Practice and Theory，2012，42(12)：1-8.

[4] 刘 萍，李永昆. 具脉冲效应和反馈控制的企业集群竞争模型的持久性分析[J]. 经济数学，2011，28(2)：1-5.LIU Ping，LI Yongkun. Analysis of Permanence of Impulsive Type Competitive Model of Enterprise Cluster with Feedback Control[J]. Journal of Quantitative Economics，2011，28(2)： 1-5.

[5] 丁同仁，李承志. 常微分方程教程[M]. 2版. 北京：高等教育出版社，2005：21-25.DING Tongren，LI Chengzhi. An Ordinary Differential Equation Course[M]. 2nd ed. Beijing：Higher Education Press，2005：21-25.

A Dynamical Analysis of a Competitive Model of Enterprises

LAO Hongyue，GE Liqian，ZHANG Maoyun，SUN Meng，CHEN Zihan，LI Feng
（School of Mathematics and Statistics，Linyi University，Linyi Shandong 276005，China）

A competitive model has been established of enterprises with a low critical point of production,followed by a study on theexistence and stability of the critical points of this system. Furthermore, a numerical simulation test has been carried out to testify the fi nal results, thus providing a theoretical explanation for the validity of this model.

competition model；critical point；stability

F207

A

1673-9833(2017)05-0083-05

10.3969/j.issn.1673-9833.2017.05.014

2017-05-27

国家自然科学基金资助项目（11601212）。

劳红月（1996-），女，山东滨州人，临沂大学学生，主要研究方向为常微分方程，E-mail：1625169290@qq.com

李 锋（1981-），男，山东临沂人，临沂大学教授，主要从事微分方程与动力系统方面的研究，E-mail：lf0539@126.com

（责任编辑：邓光辉）