非线性格兰杰因果关系在睡眠生理信号分析中的应用

2017-12-15戴加飞侯凤贞

数据采集与处理 2017年5期

杜朋戴加飞李锦王俊侯凤贞

(1．南京邮电大学图像处理与图像通信江苏省重点实验室, 南京， 210003； 2．南京军区南京总医院神经内科, 南京，210002； 3．陕西师范大学物理学与信息技术学院, 西安， 710062； 4．中国药科大学理学院, 南京，210009)

杜朋1戴加飞2李锦3王俊1侯凤贞4

基于非线性格兰杰因果关系分析睡眠生理信号。分别使用多项式核函数、高斯核函数和Sigmoid核函数将低维空间数据映射到高维特征空间,在高维特征空间使用非线性格兰杰因果方法来分析睡眠生理信号。研究结果表明，脑电信号对心电信号的影响比心电信号对脑电信号的影响更为显著，脑电信号对血压信号的影响比血压信号对脑电信号的影响更为显著，血压对心电信号的影响比心电信号对血压信号的影响更为显著,而且睡眠期样本信号间的格兰杰因果关系更为显著。仿真结果验证了睡眠期信号更能客观地反映生理信号的因果关系。

非线性格兰杰因果关系；睡眠信号；核函数

引言

睡眠是一个以不动状态为特征的基本生理过程，在典型的睡眠状态里，肢体感觉降低。睡眠普遍存在于所有的动物中，尽管它的确切功能尚未完全理解[1, 2]，但在许多重要躯体、认知和心理过程中都有重要的作用，尤其在维持正常的大脑和身体平衡方面[3]。生理信号的研究表明从清醒期到睡眠期的过渡是平稳的过程。脑电图可以较为直观地反映大脑组织的脑电活动和功能状态，因而在睡眠信号研究过程中，脑电(Electroencephalogram, EEG)信号一直是重要的工具[4]。睡眠过程受自主神经系统的调节，心电(Electrocardlogram, ECG)信号变化在反映自主神经对心脏活动的调节及评价自主神经功能方面，比其他生理参数有着更好的特异度和灵敏度[5]。血压与睡眠有较为密切的关系[6]，对高血压患者在基础治疗情况下进行睡眠干预，往往可以取得较好的效果。睡眠期脑电由于主观思维的干扰较少，从而更能客观反映生理活动状态。本文的研究点便是心电信号、脑电信号和血压信号这3种信号间的因果关系，以及睡眠对这3种信号间因果关系的影响。

在分析生理信号的过程中，不仅需要分析各个信号的同步状态，也要研究信号间的因果关系。通过分析因果关系可以确定子网络之间相互影响的方向和大小，从而降低复杂网络分析的难度。目前分析信号因果关系的主流方法包括信息论中基于条件转移熵的分析方法，然而当参数较多时，转移熵的计算将会非常复杂。另一个主流的方法便是由格兰杰提出的，格兰杰因果关系认为，如果引入第二个时间序列,可以使得第一个时间序列预期估值误差方差减少，则认为第二个时间序列是第一个时间序列的因[7]。经过西蒙斯的发展，格兰杰因果检验作为一种计量方法已经被经济学家普遍接受并广泛使用。格兰杰最初提出这个概念时只是对变量均值之间因果关系的一种考察，广泛使用的方法也只验证了变量之间的线性关系，而在非线性序列领域，传统的格兰杰因果检验不再适用。在较长时间的实验研究中都假设所检验的序列是平稳的，而实际情况下时间序列往往是非平稳的，这时线性的分析方法往往导致信息的丢失，如果使用线性格兰杰因果关系来分析数据，很可能得到错误的结论。为了促进睡眠生理信号的进一步研究，本文采用非线性格兰杰因果关系指数来对睡眠生理信号进行分析，讨论睡眠脑电信号和心电信号以及血压信号之间的因果关系。

为了将线性格兰杰因果关系扩展到非线性特征空间，本文引入核函数方法。通过核函数特征映射，将低维输入空间中的线性不可分数据映射成高维特征空间(可再生Hilbert空间)[8]中的线性可分数据。特征空间的内积可以通过某个核函数来表示，核函数的本质是对应于高维空间的内积，从而生成高维空间的特征映射,而高维空间的数据处理可借用核方法的该对应关系使用非线性映射来实现[9]

1 基本原理

1.1 线性格兰杰因果关系模型

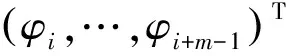
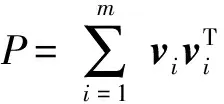
线性格兰杰因果系数为

(1)

1.2 非线性格兰杰因果关系模型

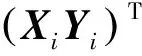
计算得到格兰杰因果系数为

(2)

2 睡眠生理信号的非线性格兰杰因果分析

2.1 实验数据

本节所使用的睡眠数据均来自PhysioBank的MIT-BIH Polysomnographic Database。该库中记录的是多参数睡眠数据，其中包括1导EEG信号、1导ECG信号、血压信号等多导睡眠信号，记录长度为6 h，数据采样频率为250 Hz。本文对受试者Slp04,Slp14,Slp32,Slp48,Slp41,Slp45,Slp59,Slp60,Slp61和Slp66这10个样本进行了测试，采用各自几组多导睡眠数据中的1导EEG信号，提取其中的清醒期和NREM睡眠I期的信号用于实验。为进一步验证格兰杰因果系数的普遍性，使用了由南京军区总医院从临床诊断中采集得到的正常人脑电信号。该库中记录了多参数脑电数据(包括16个导联信号)这些信号的采样周期为512 Hz且记录长度均大于1 min。本文分别从正常脑电数据中取出10组数据，取其Fp1导联信号和ECG导联信号，经实验验证，在16个导联信号中，第一导联Fp1信号区分度较好，所以下面以Fp1导联数据做分析对象。

2.2 分析方法

首先读取各组原始睡眠脑电信号，由于原始信号中包括脑电信号，血压信号以及心电信号3组信号，因此需要对这3组信号分别进行两两处理。从3组信号中取出2组，分别记为时间序列{x}和{y}，由于实验计算得到因果系数的计算结果在m=2时出现峰值，这里取m=2时间序列，对序列分别进行均值、归一化以及m次平移处理，组成矩阵X和Y，参考1.2小节中的方法，分别代入3类不同的核函数并取不同的核函数参数，即可求得相应的格兰杰因果系数矩阵。

核函数系数较为合适时可以得到明显的区分度，对于多项式核函数参数,当p=3时格兰杰因果系数计算结果较为显著;对于高斯核函数，在σ=3到σ=8的区间中计算结果相差较小，因而采用了σ=5的计算结果;对于Sigmoid核函数，需要考虑到Sigmoid核函数是有条件的正定函数，因此需要满足正定条件，本文取α=1/9，β=0可以满足正定函数的条件，计算结果也较为显著。

2.3 数值计算结果与分析

实验1验证耦Henon网络函数之间的格兰杰因果关系

由两个耦合函数生成的Henon网络表达式为

分析{x}序列和{y}序列，从表达式的形式中可以看出{x}序列是{y}序列的因。取m=2，利用3种核函数，选取不同的参数来计算Henon在1 000次循环中生成序列的格兰杰因果系数,结果分别如表1,2和3所示。

表1 多项式核函数计算得到的Henon网络x→y方向格兰杰因果系数

表2 高斯核函数计算得到的Henon网络x→y方向格兰杰因果系数

表3 Sigmoid核函数计算得到的Henon网络x→y方向格兰杰因果系数

从表1可以看出x→y方向的格兰杰因果系数总是非零,而且在p=2时取得最大值，这说明了Heanon网络间的因果影响是平方级数的，这也和表达式相一致。从表2和表3可以看出，x→y方向的格兰杰因果系数总是非零，参数σ和β在一定范围内的变动对结果影响较小。这表明理想情况下使用3种核函数计算格兰杰因果系数均可以得到正确的结论，对比计算结果可以发现当使用合适的参数时，多项式核函数计算的因果系数更大，而且最大值对应的参数与表达式的阶数相一致。同时，高斯核函数与Sigmoid核函数对参数的敏感度较小，因而计算结果的均方差值较小。

实验2验证样本不同时期脑电和心电信号的格兰杰因果关系

通过分别计算清醒期和睡眠期不同样本脑电和心电信号的格兰杰因果系数，可以得到脑电和心电信号格兰杰因果关系图，使用3种核函数的结果分别如图1和图2所示。

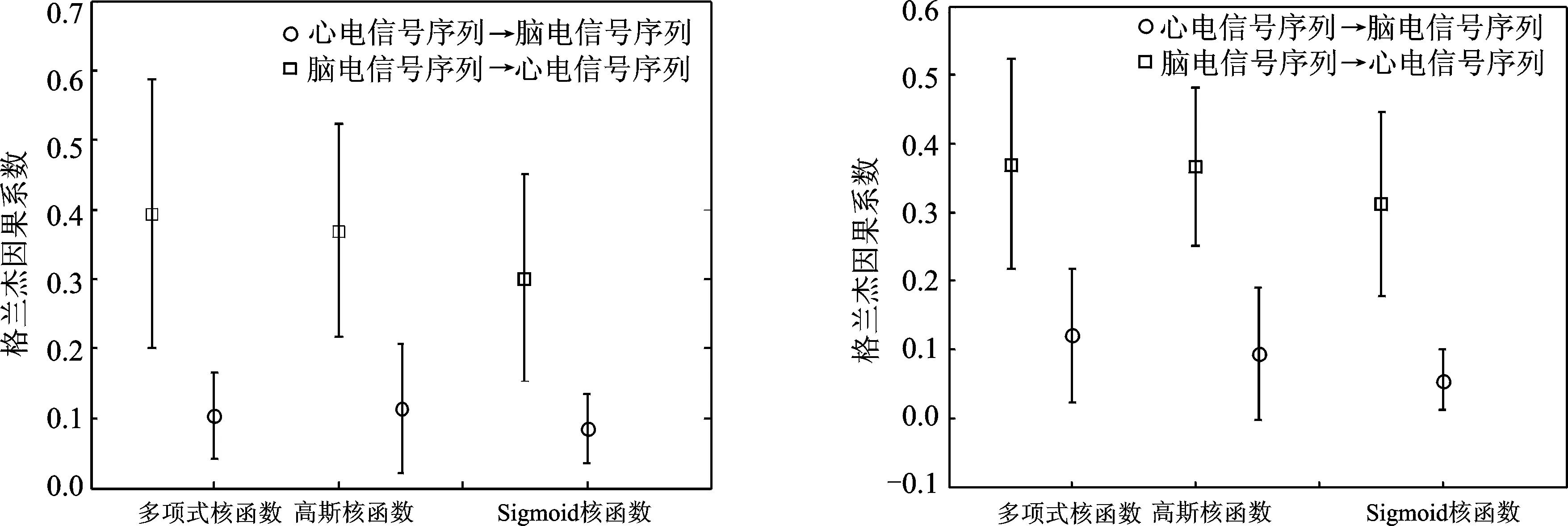
图1 清醒期脑电信号与心电信号格兰杰因果系数棒图图2 睡眠期脑电信号与心电信号格兰杰因果系数棒图

Fig.1 Granger causality index error bar chart of awake sample's EEG and ECG signals Fig. 2 Granger causality index error bar chart of sleep sample's EEG and ECG signals

使用统计产品与服务解决方案软件(Statistical product and service solutions, SPSS)对清醒期的样本均值进行样本独立t检验，即对两样本均数差别的显著性进行检验。多项式核函数，高斯核函数和Sigmoid核函数对应格兰杰因果系数的显著性水平p值分别为0.018，0.023和0.033，三者的显著性水平均小于0.05，因此可以通过置信度为0.95的t检验。同样使用SPSS对睡眠期样本均值进行样本独立t检验。多项式核函数高斯核函数和Sigmoid对应格兰杰因果系数的显著性水平更p值为0.018，0.006和0.008，三者的显著性水平均小于0.05，因此可以通过置信度为0.95的t检验。

对比清醒期和睡眠期的因果关系显著性水平，可以发现睡眠期的生理信号因果关系显著性水平更为明显。脑电信号对于心电信号有着较为明显的因果关系，即脑电信号是心电信号的因，而心电信号不是脑电信号的因。

实验3验证样本不同时期血压和脑电信号的格兰杰因果关系

通过分别计算清醒期和睡眠期不同样本脑电和血压信号的格兰杰因果系数，可以得到脑电和血压信号因果关系图，使用3种核函数的结果分别如图3和图4所示。

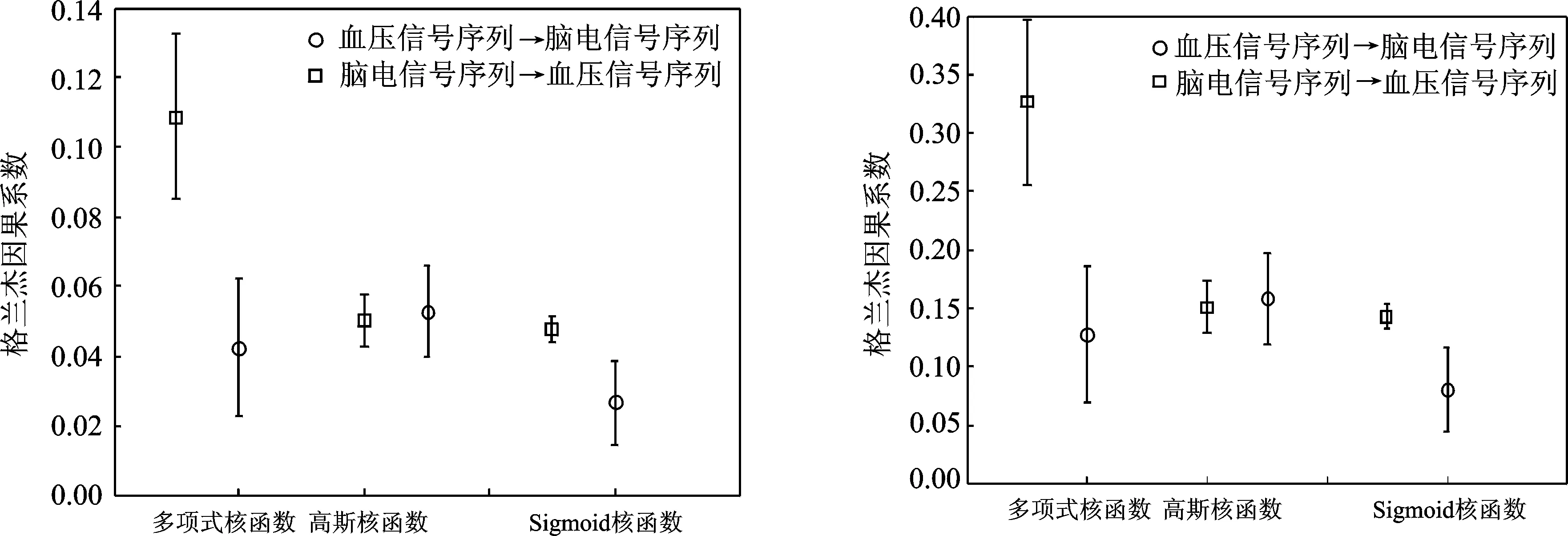
图3 清醒期脑电信号与血压信号格兰杰因果系数棒图图4 睡眠期脑电信号与血压信号格兰杰因果系数棒图

Fig.3 Granger causality index error bar chart of awake sample′s blood pressure and EEG signals Fig.4 Granger gausality index error bar chart of sleep sample′s blood pressure and EEG signals

使用SPSS对清醒期样本均值进行样本独立t检验，多项式核函数，高斯核函数和Sigmoid核函数对应格兰杰因果系数的显著性水平p值分别为0.001，0.34和0.030，多项式核函数和Sigmoid核函数对应的显著性水平均小于0.05，因此可以通过置信度为0.95的t检验，而高斯核函数则无法通过t检验，即无法利用高斯核函数来确定脑电血压信号的因果关系；使用SPSS对睡眠期样本均值进行样本独立t检验，多项式核函数高斯核函数和Sigmoid核函数对应格兰杰因果系数的显著性水平p值分别为0.006，0.35和0.045，其中多项式核函数和高斯核函数对应的显著性水平均小于0.05，因此可以通过置信度为0.95的t检验，Sigmoid核函数则无法通过t检验，即无法利用Sigmoid核函数来确定脑电血压信号的因果关系。

对比清醒期和睡眠期的样本脑电血压信号可以发现，由多项式核函数计算得到的格兰杰因果关系均具有较高显著性水平，即脑电信号是血压信号的因，血压信号不是脑电信号的因。

实验4验证样本不同时期血压和心电信号的格兰杰因果关系

分别计算清醒期和睡眠期不同样本血压和心电信号的格兰杰因果系数，可以得到血压和心电信号因果关系图，使用3种核函数的结果分别如图5和图6所示。

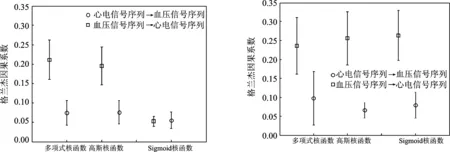
图5 清醒期血压信号与心电信号格兰杰因果系数棒图图6 睡眠期血压信号与心电信号格兰杰因果系数棒图

Fig.5 Granger causality index error bar chart of awake sample′s blood pressure and ECG signals Fig.6 Granger causality index error bar chart of sleep sample′s blood pressure and EEG signals

使用SPSS对样本均值进行样本独立t检验，多项式核函数,高斯核函数和Sigmoid核函数对应格兰杰因果系数的显著性水平p值为0.001，0.002和0.098。由于多项式核函数和高斯核函数对应的显著性水平均小于0.05，因此可以通过置信度为0.95的t检验，而Sigmoid核函数则无法通过t检验，即无法利用Sigmoid核函数来确定心电信号和血压信号的因果关系。使用SPSS对样本均值进行样本独立t检验，多项式核函数对应格兰杰因果系数的显著性水平p值分别为0.002，0.003和0.008，三者的显著性水平均小于0.05，因此可以通过置信度为0.95的t检验。

对比清醒期和睡眠期的因果关系系数，可以发现睡眠期样本的格兰杰因果关系系数显著性水平更高。血压信号对心电信号因果影响显著性较高，即心电信号是血压信号的因，血压信号不是心电信号的因。

实验5脑电采集样本脑电和心电信号的格兰杰因果关系

通过计算南京军区总医院临床采样正常样本的脑电信号和心电信号的格兰杰因果系数可以得到图7。

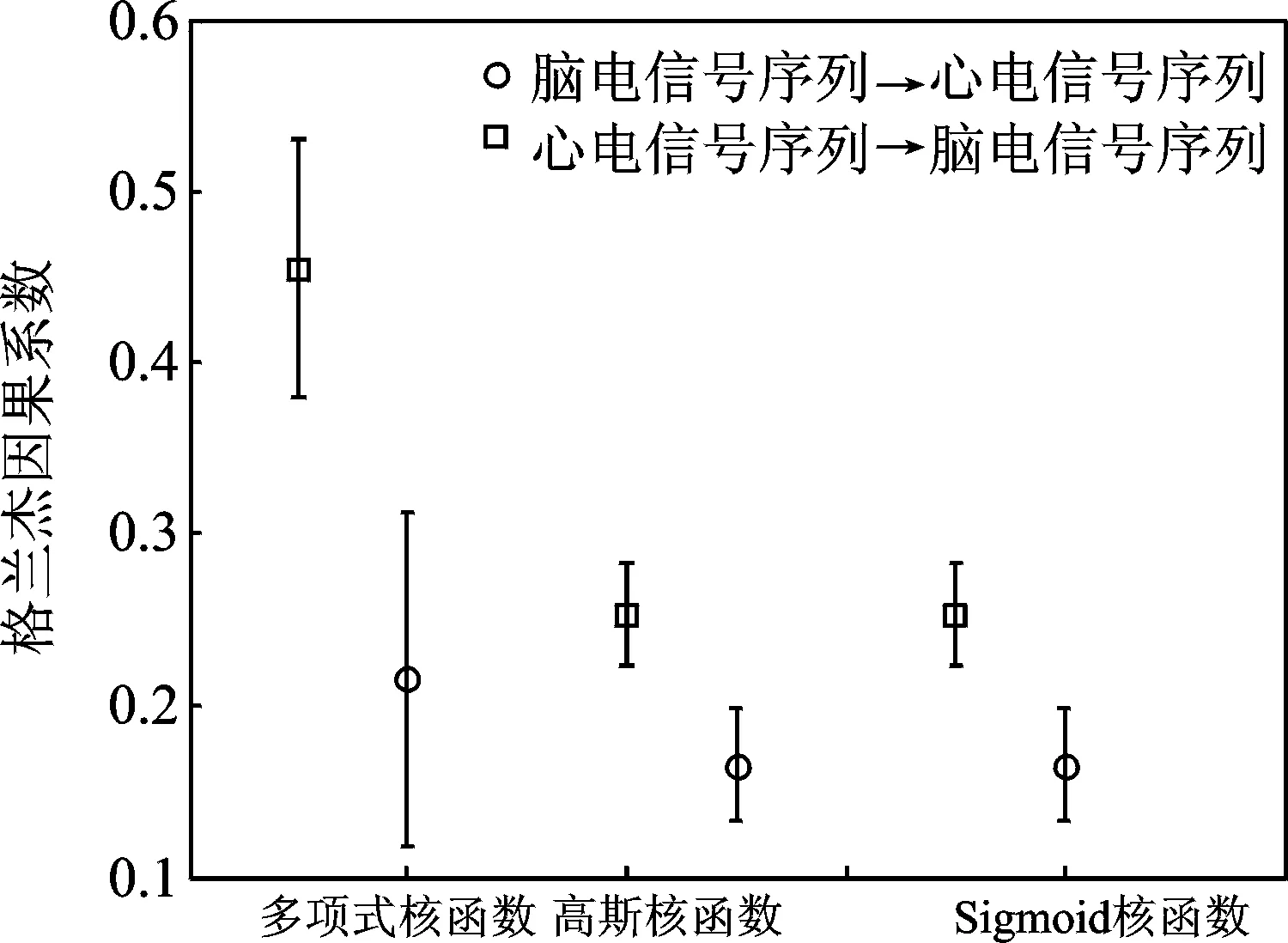
图7 3种核函数计算得到的正常样本心电信号和脑电信号格兰杰因果系数棒图Fig.7 Granger causality index error bar chart of normal sample′s EEG and ECG signals

从图7可知，使用SPSS对样本均值进行样本独立t检验，多项式核函数高斯函数和Sigmoid核函数对应格兰杰因果系数的显著性水平p值分别为0.001，0.001和0.002，三者的显著性水平均小于0.05，因此可以通过置信度为0.95的t检验。

从实验结果可以看出，正常样本脑电信号对心电信号的格兰杰影响较为显著，心电信号对脑电信号的影响很小。比较3种核函数得到的计算结果可以发现，使用合适的参数时多项式核函数计算的结果显著性水平较高，高斯核函数和Sigmoid核函数计算结果均方差较小。

3 结束语

基于非线性格兰杰因果关系的睡眠脑电分析，本文利用核函数方法将线性格兰杰因果关系扩展到非线性空间，从而可以更为准确地分析生理信号。通过对实验结果的分析发现，心电信号、脑电信号和血压信号之间存在着较为显著的因果关系，脑电对心电信号的影响比心电对脑电信号的影响更为显著，脑电对血压信号的影响比血压对脑电信号的影响更为显著，血压对心电信号的影响比心电对血压信号的影响更为显著。即脑电信号是心电信号的因，心电信号是血压信号的因，反之则无法确定。此外，相对于样本清醒期的数据分析结果，样本睡眠期的这种显著程度更为强烈，从而验证了睡眠期的生理信号可以更为清晰地反映生理活动状态。

[1] Fortune M H. State transitions between wake and sleep, and within the ultradian cycle, with focus on the link to neuronal activity[J]. Sleep Medicine, 2004, 8(6): 473-485.

[2] Saper C, Scammell T. The sleep switch: Hypothalamic control of sleep and wakefulness[J]. Trends Neurosci, 2001, 24(12): 726-731.

[3] Urrila A S, Paunio T, Palom E, et al. Sleep in adolescent depression: Physiological perspectives[J]. Acta Physiol, 2015, 213:758-777.

[4] 张莉, 何传红, 何为, 等. 基于典型相关分析与低通滤波的肌电伪迹去除 [J] .数据采集与处理, 2010, 25(2): 255-258.

Zhang Li, He Chuanhong, He Wei, et al. Method for removing EMG artifacts based on CCA and low-pass filtering [J]. Journal of Data Acquisition and Processing, 2010, 25(2): 255-258.

[5] Lee A H, Mojica J, Thomas R J, et al. Dissociation of EEG and autonomic sleep physiology[J]. Sleep Medicine, 2015, 16(2): 308-309.

[6] Schmidt E M, Linz B, Diekelmann S, et al. Effects of an interleukin-1 receptor antagonist on human sleep, sleep-associated memory consolidation, and blood monocytes[J]. Brain Behavior and Immunity, 2015, 47:178-185.

[7] Granger C W J. Investigating causal relations by econometric models and cross-spectral meth[J]. Econometrica, 1969, 37(3): 424-438.

[8] Marinazzo D, Pellicoro M, Stramaglia S. Kernel method for nonlinear granger causality[J]. Phys Rev Lett, 2008, 100(14): 144103.

[9] Schoelkopf B, Muandet K, Fukumizu K, et al. Computing functions of random variables via reproducing kernel Hilbert space representations[J]. Statistics and Computing, 2015, 25(4): 755-766.

[10] 刘柳，陶大程. Lasso问题的最新算法研究 [J] .数据采集与处理, 2015, 30(1): 35-46.

Liu Liu, Tao Dacheng. Review on recent mehtod of solving Lasso problem [J]. Journal of Data Acquisition and Processing, 2015, 30(1): 35-46.

[11] Marinazzo D， Pellicoro M, Stramaglias S. Kernel-Granger causality and the analysis of dynamical networks[J]. Physical Review E, 2008, 77(2)： 056215.

[12] Camps-Vallsa G, Martin-Guerreroa J D, Rojo-Alvarez J L, et al. Fuzzy sigmoid kernel for support vector classifiers[J]. Neurocomputing, 2004, 62(1): 501-506.

ApplicationofNonlinearGrangerCausalityinAnalysisofPhysiologicalSignalsDuringSleep

Du Peng1， Dai Jiafei2， Li Jin3， Wang Jun1， Hou Fengzhen4

(1．Image Processing and Image Communications Key Lab. , Nanjing University of Posts & Telecomm, Nanjing, 210003, China； 2．Nanjing General Hospital of Nanjing Military Command, Nanjing, 210002, China； 3．College of Physics and Information Technology, Shanxi Normal University, Xi′an， 710062, China；4．School of Science, China Pharmaceutical University, Nanjing， 210009, China)

A method based on the nolinear Granger causality is used to analyze sleep physiological signal. Polynomial kernel function, Gaussian kernel function and sigmoid kernel function are used to map the linear data in low dimensional input space into high dimensional feature space in which linear Granger method can be used to analyse the biomedical signals. The analysis results show that the causal effect of electrocardlogram (ECG) signals to electroencephalogram (EEG) signals, ECG signals to blood pressure signals and blood pressure signals to ECG signals are more significant than that of the opposite direction. In addition, the results of sleep subjects have more significant difference than that of normal subjects. The simulation results validate that the sleep physiological signal reflects the causality more objectively.

nonlinear Granger causality； sleep signal； kernel function

国家自然科学基金(61271082， 61401518)资助项目；江苏省重点研发计划(BE2015700)资助项目；江苏省自然科学基金(BK20141432资助项目)；南京军区南京总医院基金(2014019)资助项目；南京市医疗卫生科技项目(201503009)资助项目；中国药科大学中央高校基本科研业务费专项资金(FY2014LX0039)资助项目。

2015-11-18；

2016-03-23

TP911.73