基于特征选择的相对k子凸包分类方法

2017-12-15牟廉明刘好斌

数据采集与处理 2017年5期

关键词：特征选择正则邻域

牟廉明刘好斌

(1.内江师范学院数学与信息科学学院，内江, 641100;2.数据恢复四川省重点实验室，内江, 641100)

基于特征选择的相对k子凸包分类方法

牟廉明1,2刘好斌1,2

(1.内江师范学院数学与信息科学学院，内江, 641100;2.数据恢复四川省重点实验室，内江, 641100)

k子凸包分类方法在实际问题中有广泛应用。但随着问题维数的增加，该方法计算得到的凸包距离非常接近甚至相等，这严重影响了分类性能。针对此问题，本文设计了一种基于特征选择的相对k子凸包分类方法。首先根据绝对凸包距离存在的不足引入相对k子凸包距离，然后在k邻域内利用判别正则化技术进行特征选择，并将特征选择融入相对k子凸包优化模型中，为每个测试样本在不同的类别中学习一个自适应的特征子集，从而得到一个用于分类的有效相对k子凸包距离。实验结果表明，该方法不仅能够进行特征选择，而且分类性能也有了明显提高。

相对k子凸包分类；自适应；判别正则化；特征选择

引言

融合支持向量机、k近邻和凸包技术的优点来提高分类器性能已经有许多卓有成效的研究[1-3]。Vincent和Bengio在k近邻基础上利用支持向量机分类思想和凸包技术提出一种k局部凸包最近邻分类算法[4](k-local convex distance nearest neighbor algorithm, CKNN)。CKNN算法使用到每个类的局部凸包距离来代替k近邻中的样本距离，不仅具有k近邻的不需提前训练应用时直接测试、能够处理非线性决策边界问题和多分类问题等许多优点，同时等价地考虑了不可见的训练样本，增加了分类决策边界的光滑性，并改善了分类器的性能，因此在生命科学、人脸识别和图像处理等领域有广泛的应用[4,5]。

在实际应用中，CKNN算法仍然存在很多的不足。针对实际问题中由于类数很多从而导致时间复杂度高和样本环状分布的问题，文献[6]将求解凸包距离限制在一个k邻域内，给出了k子凸包分类方法(ksub-convex-hull classifier,kCH)，有效地抑制了类数多和样本环状分布对分类性能的影响；针对kCH对k值比较敏感，文献[7]利用度量学习和集成技术来提升kCH的分类性能；针对CKNN算法对噪声比较敏感的问题，文献[8]提出了相对局部超平面分类算法，利用人类的相对感知特点，通过变换将原始数据空间转化到一个相对距离空间，然后在相对距离空间内应用局部超平面进行分类来抑制噪声的影响；针对噪声对kCH算法的影响以及在k邻域内经常出现的不同类样本数严重不平衡的情况，文献[9]设计了选择性自适应k子凸包算法，该算法根据凸包和噪声特点，利用留一法来去除冗余数据和噪声，从而提升了分类性能。针对高维数据，如何有效选择k邻域样本，Yang T和Kecman V采用特征加权技术对CKNN进行改进并提出了自适应局部超平面分类[10]方法，并进一步改进将其应用于人脸识别[5]；文献[11]设计了基于局部判别分析的超平面分类算法，利用局部判别技术来提取特征，提升分类性能。但是，以上方法的特征选择和凸包计算是分离的，当问题维数变大时，计算得到的到每个类的凸包距离经常非常接近，甚至相等，从而导致了分类性能的下降。

本文通过引入相对凸包距离来克服目前应用绝对凸包距离分类存在的不足；然后利用判别正则化技术，将特征选择嵌入相对凸包计算的优化模型中，为每一个测试样本在每一个类中学习一个自适应的特征子集，从而达到降维的目的。在16个UCI数据集和4个人脸数据集上的实验结果表明，该方法的分类性能有明显提高。

1 相关定义

从凸包构成的方法来分类，凸包分类技术大体可以分为两种[9]：第一种是全局凸包分类，如最近邻凸包分类[12,13]，其基本思想是将每一类的所有训练样本构成一个全局凸包，对每一个测试样本，通过计算它到每个类的全局凸包距离来进行分类。显然这类算法对噪声和类的数目比较敏感，对复杂结构分类效果较差，分析大数据的时间复杂度很高。第二种是局部凸包分类，如CKNN[4]和kCH[6]，其基本思想是通过计算测试样本到每个类中最近的k个样本构成的局部凸包距离来进行分类。

定义1(凸包)[4,6]：设S⊂Rn，S={d1,d2,…,dk}是由Rn中k个点组成的集合，则定义S的凸包为

(1)

定义2(凸包距离)[4,9]：对∀x∈Rn，S⊂Rn，则x到S的绝对凸包距离为

(2)

定义3(k子凸包分类)[6,9]：设Nk(x)为测试样本x的k邻域，si={d1,d2,…,dp}⊆Nk(x)为x的k邻域中第i类样本子集，L(x)={L1,L2,…,Lq}为x的k邻域所包含的类的集合，则x的类别为

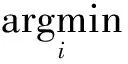
(3)

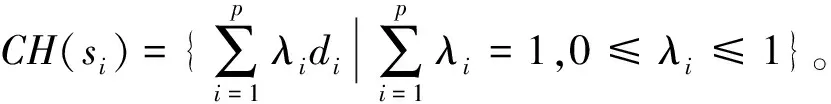
其主要想法是利用x到它的k邻域中每个类子凸包绝对距离的最小值来判定x的类别。

2 相对k子凸包分类

绝对k子凸包距离通过计算到类C的绝对距离来度量相似性，随着类数增多、维数增加，经常会出现凸包距离非常接近或相等的情况；同时，即使到类C的凸包距离小，也许此时到其他类的凸包距离也很小，因此仅仅利用绝对凸包距离来判断类别会导致分类性能的下降。下面借鉴SVM中的二分类思想，引入相对k子凸包距离。

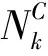
(4)

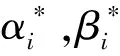
(5)

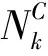
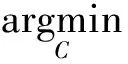
(6)

其主要思想是利用测试样本x到它的k邻域中每个类的相对k子凸包距离的最小值来判定x的类别。

3 基于特征选择的相对k子凸包分类

特征选择[14,15]是分类器设计中的一个重要环节。为了进一步提高计算相对k子凸包距离的有效性，降低维数，提高分类性能，本文设计了一个基于特征选择的相对k子凸包分类算法(Relativeksub-convex-hull classifier based on feature selection, FRCH)，该算法主要利用了两项技术：(1)在k邻域内通过引入相对凸包距离来代替绝对凸包距离；(2)在k邻域内通过利用判别正则化技术[16]来进行特征选择，并将特征选择融入相对凸包距离优化模型中。这样就可为不同的测试样本根据不同的邻域和不同的类别学习一个自适应的特征子集，相应的计算结果可得到每个类的有效相对凸包距离。

3.1 基于判别正则化的特征选择

为了进行特征选择，将k邻域中的类内和类间信息作为判别先验知识直接引入到正则化项的构建中，即在k邻域中，类内样本尽可能靠近，类间样本尽可能远离[16]。

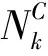
(7)

(8)

则类内紧性度量定义为

(9)

则类间分散性度量定义为

(10)

因此判别正则化项为

A(η)=ηSw-(1-η)Sb

(11)

式中η为正则化参数，用以平衡类内紧性和类间分散性之间的相对重要性。

3.2 基于特征选择的相对k子凸包分类模型

为了实现特征选择，达到降维目的，将正则化项嵌入到相对k子凸包计算模型中，得到的优化模型为

(12)

(13)

FRCH不仅具有k子凸包分类的优点，克服了绝对凸包距离存在的不足，而且通过正则化技术将分类和特征选择融合在一起，能够处理大数据、高维情况下的特征选择和分类任务，提升了分类性能。

4 实验及结果分析

应用16个UCI数据集[17]和4个人脸识别数据集[18]做对比实验，数据集具体信息如表1所示。在对比实验中，对每个数据集采用10次10倍交叉验证来比较3种算法的性能，用平均分类错误率以及标准偏差作为评价算法性能的指标。所有的实验都在相同的数据划分和相同的实验环境下进行。

FRCH算法是在CKNN[4]算法与kCH[6]算法的基础上引入相对凸包距离和判别正则化技术进行的改进。因此为了验证FRCH算法的性能，选择以上两种算法与其进行对比。

FRCH算法通过求解一个二次规划问题来计算相对凸包距离，时间复杂度与CKNN和kCH同为O(n2)，实际计算时间与邻域的样本数和问题的类数有关。由于在计算优化模型时多了一个相对凸包距离项和判别正则化项，所以实际计算时间约高于CKNN和kCH，但是在一个k邻域中数据量不大时，实际应用中可以接受。

表2列出了3种算法在不同数据集上的分类错误率对比结果。由表2可知，FRCH算法在所有数据集上都明显优于CKNN算法和kCH算法。对10次10倍交叉验证的实验结果，在显著性水平为0.05时进行t检验，得到：对于分类准确性，FRCH算法在20个数据集上都显著优于CKNN算法，在16个数据集上显著优于kCH算法。因此，FRCH分类算法在分类精度上有显著提高。

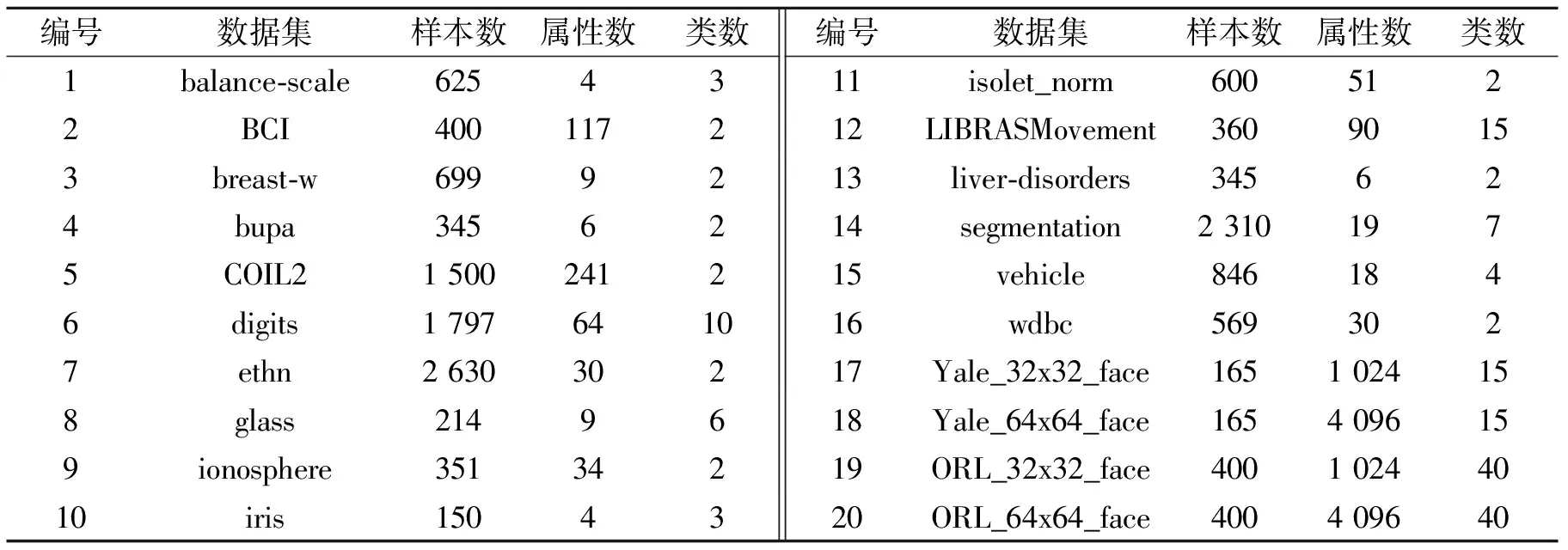
表1 实验数据集

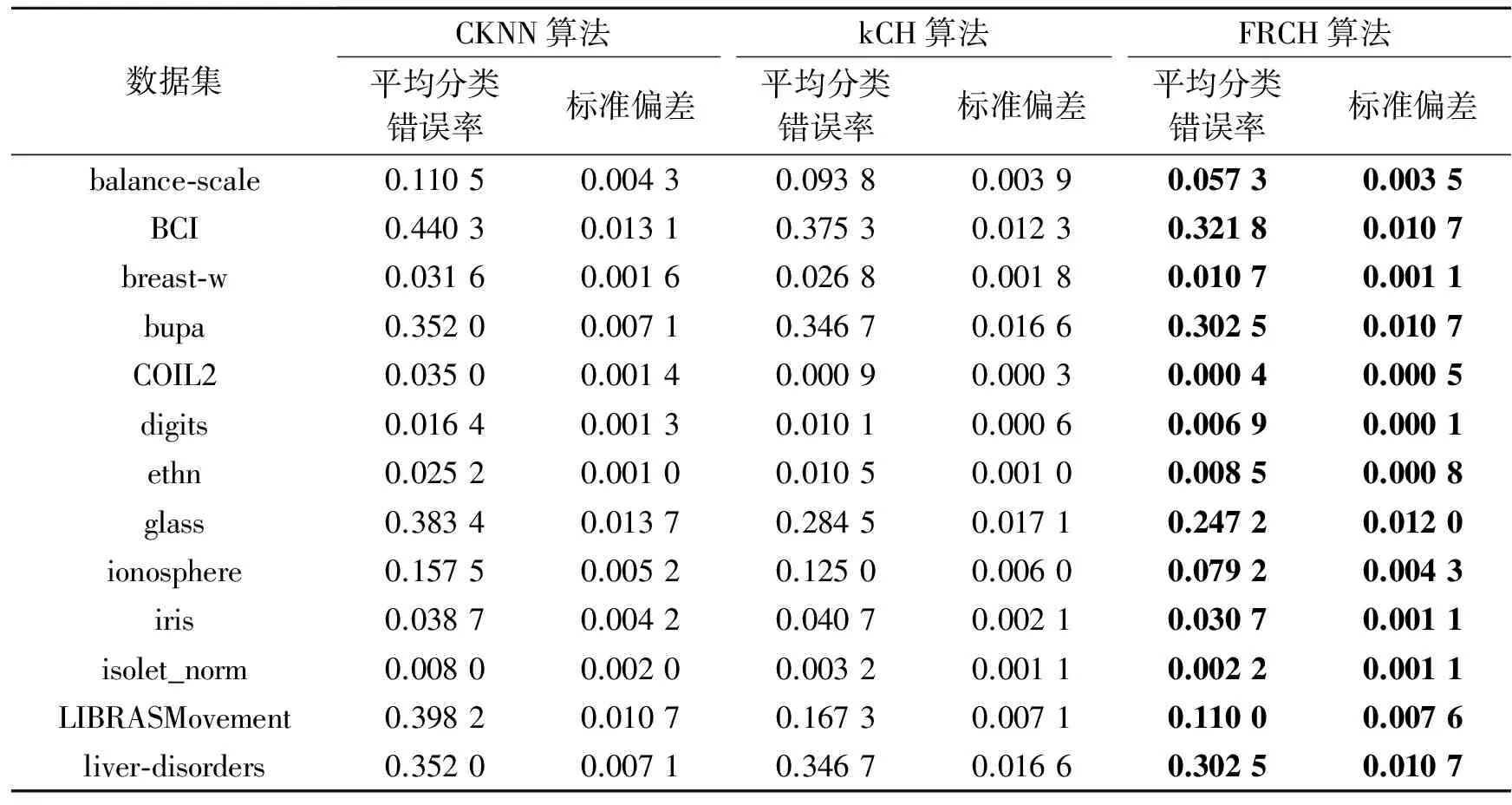
表2 3种算法在不同数据集上的分类错误率比较

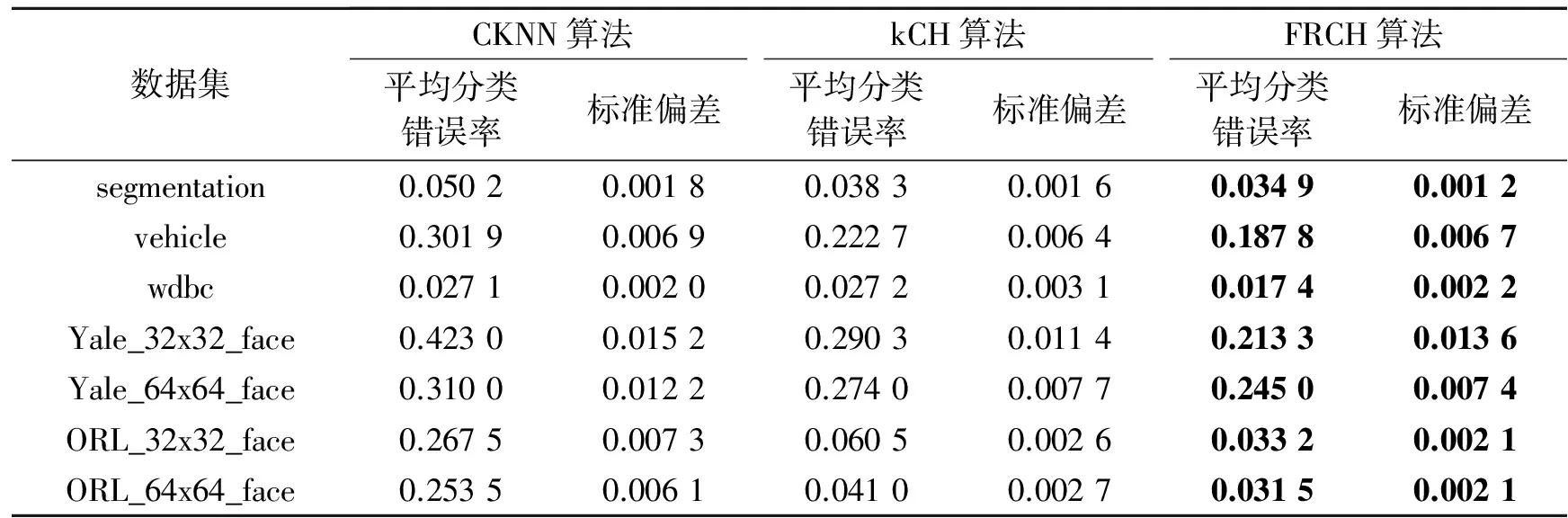
(续表)

5 结束语

由于k子凸包分类算法仅仅考虑数据集的局部分布特点，结合网格技术可以较好地处理大数据分析问题，所以在数据挖掘中有广泛的应用。但在处理高维数据时如何提高其分类性能一直是一个研究热点。目前的改进算法没有把特征选择和分类算法有效结合起来，本文针对k子凸包分类方法的不足进行深入分析，引入相对k子凸包距离计算方法，同时在k邻域内利用正则化技术进行降维，将特征选择和凸包分类结合起来，设计了一种有效的相对k子凸包分类方法，解决了绝对k子凸包距离分类存在的不足，能够有效运用于数值型数据分类分析中。实验结果表明，FRCH方法在分类性能上均明显优于kCH和CKNN算法。但是，如何有效地同时处理大数据、高维数据、抑制噪声和处理复杂数据类型，仍然需要深入研究。为了进一步提高该方法的分类性能，下一步将探讨在大数据集情况下，如何利用半监督方法和集成学习技术来克服该算法对k邻域选择的敏感性，提高FRCH算法的分类性能；同时改进算法来处理非数值型数据和混合型数据类型，进一步拓展FRCH的应用领域。

[1] Miguel C, Julio L, Sebastián M. A multi-class SVM approach based on the l1-norm minimization of the distances between the reduced convex hulls[J]. Pattern Recognition, 2015(48): 1598-1607.

[2] 邹永祥，吴宗亮．一种广义不可分的支持向量机算法[J]．数据采集与处理，2015, 30(2): 434-440.

Zou Yongxiang, Wu Zongliang. Generalized C-support vector machine algorithm[J]. Journal of Data Acquisition and Processing, 2015，30(2):434-440.

[3] 刘绍毓，周杰，李弼程，等．基于多分类SVM-KNN的实体关系抽取方法[J]．数据采集与处理，2015, 30(1):202-210.

Liu Shaoyu, Zhou Jie, Li Bicheng, et al. Entity relation extraction method based on multi-svm-knn classifier [J]. Journal of Data Acquisition and Processing, 2015, 30(1):202-210.

[4] Vincent P, Bengio Y. K-local hyperplane and convex distance nearest neighbor algorithms[J]. Advances in Neural Information Processing Systems, 2001: 985-992.

[5] Yang T, Kecman V. Face recognition with adaptive local hyperplane algorithm[J]. Pattern Anal Applic, 2010(13): 79-83.

[6] 牟廉明．k子凸包分类[J]．山西大学学报(自然科学版)，2011, 34(3): 374-380.

Mou Lianming. Aksub-convex-hull classifier [J]. Journal of Shanxi University(Natural Science)，2011, 34(3): 374-380.

[7] 牟廉明．基于度量学习的邻域k凸包集成方法[J]．合肥工业大学学报(自然科学版)，2013,36(2): 171-175.

Mou Lianming. Neighbork-convex-hull ensemble method based on metric learning[J]. Journal of Hefei University of Technology, 2013,36(2): 171-175.

[8] Wen Guihua, Jiang Lijun, Wen Jun, et al. Perceptual relativity-based local hyperplane classification[J]. Neurocomputing, 2012, 97: 155-163.

[9] 牟廉明．选择性自适应k子凸包分类方法[J]．南京大学学报(自然科学版)，2013, 49(4): 410-416.

Mou Lianming. Selective adaptiveksub-convex-hull classifier[J]. Journal of Nanjing University(Natural Sciences), 2013, 49(4): 410-416.

[10] Yang Tao, Kecman V. Adaptive local hyperplane classification[J]. Neurocomputing, 2008(71): 3001-3004.

[11] Xu Jie, Yang Jian, Lai Zhihui. K-local hyperplane distance nearest neighbor classifier oriented local discriminant analysis[J]. Information Sciences, 2013, 232(5): 11-26.

[12] Zhou X F, Shi Y. Nearest neighbor convex hull classifier based on subspace sample selection[J]. Computer Engineering, 2008, 34(12): 167-168.

[13] Zhou X F, Shi Y. Nearest neighbor convex hull classification method for face recognition[J]. Lecture Notes in Computer Science, 2009, 5545: 570-577.

[14] Zhang Ping， Guo Xi. A cascade face recognition system using hybrid feature extraction[J]. Digital Signal Processing，2012，22：987-993.

[15] Dhanjal C，Gunn S R，Shawetaylor J. Efficient sparse kernel feature extraction based on partial least squares[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2009， 31(8)：1347-1361.

[16] Xue H, Chen S, Yang Q. Discriminatively regularized least-squares classification[J]. Pattern Recognition, 2009, 42(1):93-104.

[17] Asuncion A, Newman D J. UCI machine learning repository [DB/OL]. [2015-07-10] http://www.ics.uci.edu/～mlearn /MLRepository.html.

[18] Cai Deng, He Xiaofei. Face databases[DB/OL]. [2015-07-10]http://www.zjucadcg.cn/dengcai/Data/FaceData.html.

RelativekSub-Convex-HullClassifierBasedonFeatureSelection

Mou Lianming1,2, Liu Haobin1,2

(1.College of Mathematics and Information Science, Neijiang Normal University, Neijiang, 641100, China；2.Data Recovery Key Laboratory of Sichuan Province, Neijiang, 641100, China)

Theksub-convex-hull classifier is widely used in practical problems. But with the increase of the dimension of the problem, these convex distances calculated by the method are very close to or even equal, which seriously affectes the performance of classification. To resolve the above problems, a relativeksub-convex-hull classifier based on feature selection (FRCH) is designed in this paper. Firstly, the definition of the relativeksub-convex-hull is introduced according to the shortcomings of absolutely convex hull distance. Then, the feature selection is carried out by using the discriminant regularization technique in thekneighborhood. Moreover, the feature selection method is embedded in the optimization model on the relativekconvex hull. Through these efforts, an adaptive feature subset in different categories for each test sample can be extracted, and a valid relativeksub-convex-hull distance can be obtained. Experimental results show that our FRCH not only can make the feature selection practicable, but also significantly improves the classification performance of theksub-convex-hull classifier.

relativeksub-convex-hull classifier; adaptive; discriminant regularization; feature selection

国家自然科学基金(10872085)资助项目；四川省科技厅科技计划重点项目基金(2017JY0199)资助项目；内江师范学院自然科学重点项目基金(12NJZ03)资助项目。

2016-03-31；

2016-04-19

TP391