一种改进的模糊认知诊断模型

2017-12-15李忧喜文益民易新河

数据采集与处理 2017年5期

关键词：诊断模型测试题主观题

李忧喜文益民,2 易新河徐智,2

(1.桂林电子科技大学计算机与信息安全学院，桂林，541004; 2.桂林电子科技大学广西可信软件重点实验室，桂林，541004)

一种改进的模糊认知诊断模型

李忧喜1文益民1,2易新河1徐智1,2

(1.桂林电子科技大学计算机与信息安全学院，桂林，541004; 2.桂林电子科技大学广西可信软件重点实验室，桂林，541004)

认知诊断模型利用学生做题的得分情况和测试题-知识点的关系来挖掘学生的潜在特质，以得到学生对知识点的掌握情况，进而可以预测学生对测试题的得分情况。但已有的认知诊断模型一般都忽视了主观题中学生对知识点的掌握数量和掌握程度及知识点的重要性对认知诊断的影响。本研究提出一种改进的模糊认知诊断模型(Revised fuzzy cognitive diagnosis framework,R-FuzzyCDF)，在主观题的诊断中假设随着学生掌握知识点的个数增多，学生正确作答的概率增高，并考虑了知识点的重要性对认知诊断的影响，实验结果表明这种改进的FuzzyCDF模型进一步提高了认知诊断的准确性。

认知诊断；连接型；补偿型；知识点重要性；主观题

引言

基于学生的学习行为或者答题结果对学生进行认知诊断具有非常重要的意义[1]。认知诊断也是学习分析学[2]的重要应用领域。测试题测试是对学生进行认知诊断的通用手段。在传统考试中，测试题一般包含主观题和客观题两种题型。主观题要求考生撰写解答过程，以表达对试题的理解，常见题型有计算题、简答题、论述题、应用题和作文题等；客观题让学生从给定的选项中选择答案，其类型有判断题和选择题等[3]。但是，传统测试只给出学生在各个测试题上的得分，而实际上往往分数相同的学生可能存在不同的知识状态，即对知识点的掌握情况。通过分析学生在测试题上的作答情况，可以诊断学生对测试题所涉及的知识点的掌握情况，从而可为学生和教师提供帮助。认知诊断模型有多种，不同的模型有不同的特点及应用条件，因此模型的选择对认知诊断的结果有重要影响[4]。国外常见的认知诊断模型有Fisher[5]提出的线性Logistic模型(Linear logistic trait model，LLTM)，Tatsuoka等[6]提出的规则空间模型(Rule space model，RSM)，Leighton等[7]提出的属性层级模型(Attribute hierarchy model，AHM)、Hartz[8]提出的融合模型(Fusion model)、Torre等[9]提出的确定输入噪音与门模型(Deterministic inputs,noisy and gate model，DINA)和高阶DINA模型。国内认知诊断理论的研究起步虽然较晚，但通过近年的发展已取得很大的进步。钱锦昕等[10]提出了基于神经网络的PSP方法，该方法由主成分分析(Principal component analysis,PCA)、自组织特征映射网(Self-organizing feature map,SOM)和概率神经网络(Probabilistic neural network,PNN)组成，并将其应用于认知诊断中，PSP首先利用PCA来确定认知属性，然后利用SOM对被试者进行分类，最后利用PNN对新的被试者进行类别判断，从而得到被试者的知识状态，该方法不需要进行复杂的参数估计，大大提高了算法的效率；康春花等[11]将0-1评分的聚类分析法扩展到多级评分，提出多级评分聚类诊断法，解决了认知诊断模型随着知识点数量增多而诊断准确率下降的问题；祝玉芳等[12]提出了一种多策略的多级评分认知诊断方法，将多级评分转化为0-1评分，然后利用0-1评分方式进行诊断，最后用多级评分诊断学生的知识点掌握情况；宋丽红等[13]提出了改进的确定输入噪音与门模型(Revised deterministic inputs, noisy and gate model,R-DINA)，R-DINA模型认为知识点之间存在联系，并假设掌握部分知识答题正确的概率要高于什么都没掌握的，从而提高了诊断准确率；吴润泽等[14]提出了一种模糊认知诊断模型(Fuzzy cognitive diagnosis framework，FuzzyCDF)，将模糊理论应用到认知诊断中，解决了传统认知诊断模型无法诊断主观题的问题。

虽然认知诊断模型的研究取得了很大进展，但是仍然还存在着一些问题。以上大部分认知诊断模型无法对主观题进行诊断，因为主观题知识结构复杂，学生的知识状态不同，但却可能得到相同分数。FuzzyCDF模型将模糊理论应用于认知诊断模型，将学生对主观题的掌握程度假设为模糊并，即学生只要掌握了测试题考查的知识点中的一个就有可能答对该测试题。但这种假设不够严谨，实际中若学生只掌握测试题所涉及的知识点中的一个，很多时候得不到分数。FuzzyCDF模型虽然提到过不同知识点对学生正确作答有不同的影响，但并未作深入分析。针对以上问题，本研究在FuzzyCDF模型的基础上提出一种改进的模糊认知诊断模型(Revised fuzzy cognitive diagnosis framework,R-FuzzyCDF)。在主观题的诊断上，R-FuzzyCDF模型假设学生掌握知识点越多，答题正确的概率也越大；R-FuzzyCDF模型同时假设知识点的重要性和难度对其掌握有着类似的影响。

1 相关工作

1.1 认知诊断

1.1.1 项目反应理论

项目反应理论，又叫潜在特质理论，是一种现代心理测量理论，目的在于指导筛选测试题和编制测试题。该理论假设每个学生都有自己的“潜在特质”。潜在特质是指学生潜在的能力，通常用答题的得分来进行估算。项目反应理论认为，通过考生对具有一定难度和区分度等特征的测试题的答题情况可以确定考生的潜在特质[15]，其中测试题的难度是一种衡量测试题难易程度的指标，测试题的区分度是指测试题对所有被测对象高低水平的鉴别能力[16]。该理论的双参数反应模型表达为

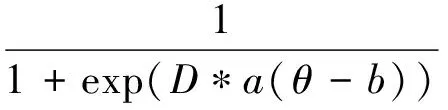
(1)

式中：α表示学生对知识点的掌握程度；a为知识点的区分度参数；b为知识点的难度参数；θ为学生的潜在特质水平；D=-1.7[17]，是一经验参数。

1.1.2 认知诊断评估

认知诊断评估是在考试的基础上，为学生或教师提供诊断信息，即关于学生对知识点掌握情况的信息[18]。认知诊断模型利用学生做题得分情况和测试题与知识点的关系来发现学生对知识点的掌握情况，从而还可以预测学生对新的测试题的得分情况。图1所示为认知诊断的过程。通过考试得到学生对测试题的得分矩阵X，测试题与知识点之间的关系用矩阵Q表示，利用得分矩阵X和Q可以进行认知诊断，从而得到学生对知识点的掌握情况。

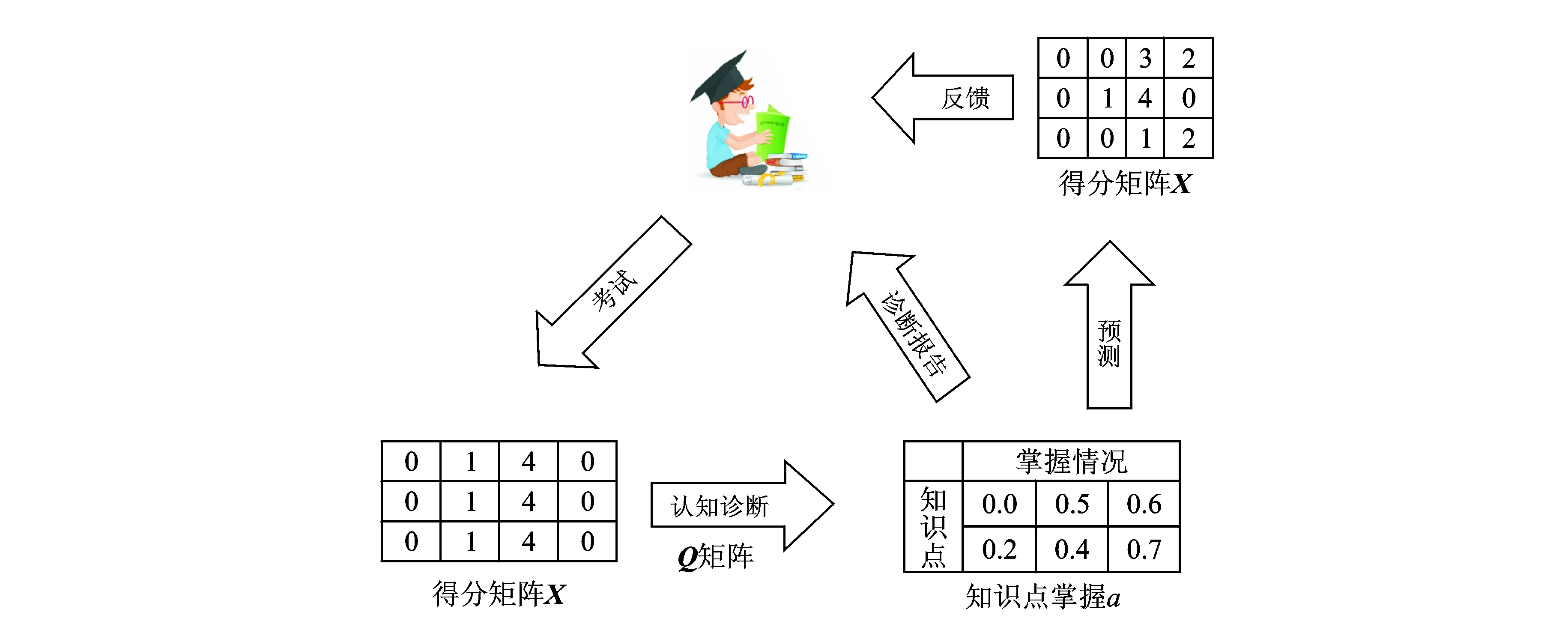
图1 认知诊断过程Fig.1 A toy example of cognitive diagnosis model

1.2 相关模型介绍

1.2.1 DINA模型

DINA模型是已有认知诊断模型中应用最广泛的模型，它定义学生i在测试题j上正确作答的概率为

P(Xij= 1|ηij,sj,gj) = (1 -sj)ηijgj(1 - ηij )

(2)

式中：Xij表示学生i在测试题j上的得分，其取值为0或1；ηij=1 表示学生i掌握了测试题j所涉及的全部知识点；ηij=0 表示学生i没有掌握测试题j所涉及的全部知识点；sj为失误率，表示掌握了测试题j所考查的所有知识点但做错的概率；gj为猜测率，表示未掌握测试题j所考查的所有知识点但通过猜测做对的概率。

该模型假设：若学生i掌握了测试题j所涉及的全部知识点，则学生i正确作答测试题j的概率等于1减去测试题j的失误率；若学生i没有掌握测试题j所涉及的全部知识点，则学生i正确作答测试题j的概率等于测试题j的猜测率。前提是假定学生i在作答测试题j时，失误和猜测不可能同时发生，而且失误或者猜测必有一种情况发生。

1.2.2 FuzzyCDF模型

FuzzyCDF模型将模糊理论应用到认知诊断中，可以同时对学生作答客观题和主观题进行诊断，解决了传统认知诊断模型无法有效诊断主观题的问题。

在FuzzyCDF模型中，学生正确作答客观题和主观题的概率计算公式分别为

P(Xij=1|ηij,sj,gj)=(1-sj)ηij+gj(1-ηij)

(3)

P(Xij|ηij,sj,gj)=N(Xij|[(1-sj)ηij+gj(1-ηij)],σ2)

(4)

式中：Xij代表学生i在测试题j上的得分，在式(3)中Xij取值为0或1，在式(4)中Xij的取值范围为[0,1]；ηij表示学生i对测试题j的掌握程度，取值为[0,1]；σ为主观题分数归一化后的方差。因此，在FuzzyCDF模型中，学生正确作答客观题的概率等于1减去失误率sj乘以学生i对题目j的掌握程度ηij与1减去学生i对题目j的掌握程度ηij乘以猜测率gj之和；正确作答主观题的概率服从以(1-sj)ηij+gj(1-ηij)为均值σ2为方差的正态分布。因此，FuzzyCDF模型假定了学生i在作答测试题j时，失误和猜测可以同时发生。

根据项目反应理论，FuzzyCDF模型假设学生i对知识点k的掌握程度由知识点相关的模糊集的隶属函数来确定，即

(5)

式中：αik表示学生i对知识点k的掌握程度，即学生i对知识点k的隶属度i(k)；aik表示知识点的区分度；bik表示知识点k对学生i的难度；θi表示学生i的潜在特质水平；D为常数等于-1.7。

FuzzyCDF模型假设在客观题作答中，学生i要掌握题目j所涉及的全部知识点，才能掌握题目j；如图2(a)所示，学生i1掌握了题目j，因为学生i1掌握了题目所考查的3个知识点，而学生i2没有掌握题目j。该模型假设在主观题作答中，学生i只要掌握题目j所涉及的全部知识点中的其一，就可能掌握题目j；如图2(b)所示，学生i1可能掌握了题目j，因为学生i1掌握了题目j所考查的两个知识点，而学生i2不可能掌握题目j。

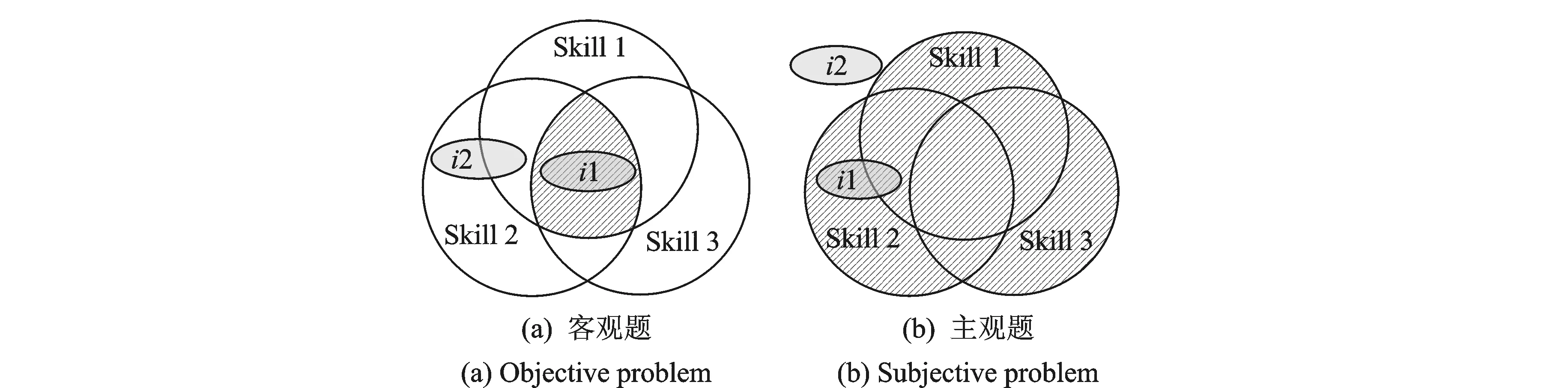
图2 题目掌握情况例子Fig.2 An example of whether a student masters a problem

因此，该模型假设在客观题中，学生i对题目j的掌握程度ηij等于学生i对知识点掌握程度的模糊交，其表达式为

ηij=i∩1≤k≤K,qjk=1(k)

(6)

式中：K表示Q矩阵中测试题所考核的知识点的个数，qjk=1表示题目j考查了知识点k，i(k)表示学生i对知识点k的掌握程度，i1≤k≤K,qjk=1(k)表示学生i对题目j所考查的知识点k的掌握程度。i∩1≤k≤K,qjk=1(k)表示学生i对题目j所考查知识点的掌握程度的交集。

FuzzyCDF模型假设在主观题中，学生i对题目j的掌握程度ηij等于对知识点掌握程度的模糊并，其表达式为

ηij=i∪1≤k≤K,qjk=1(k)

(7)

模糊理论中模糊交和模糊并的计算公式为

(A∩B)(x)=min(A(x),B(x))

(8)

(A∪B)(x)=max(A(x),B(x))

(9)

因此，式(6,7)可以理解为取学生i对题目j所考查全部知识点掌握程度的最小值或最大值作为学生i对题目j的掌握程度。

2 R-FuzzyCDF模型

2.1 模型假设

2.1.1 假设1

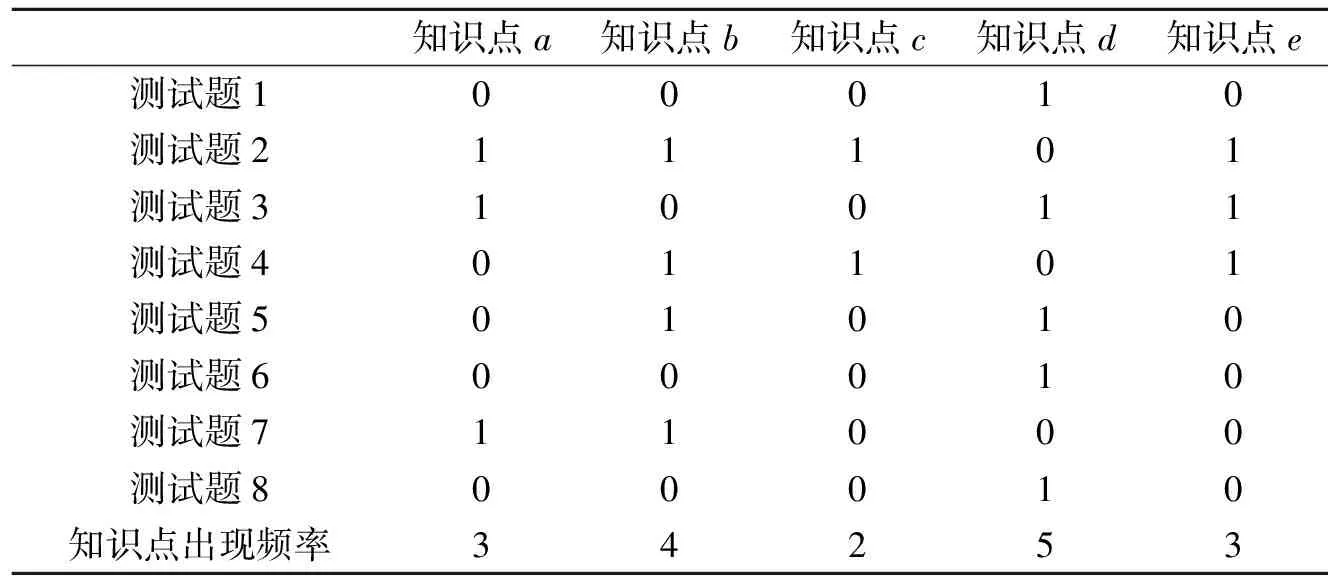
知识点是题目的基本组成单位，也是学生学习的基本认知单位。知识点的相关属性包括知识点的难易程度、知识点的重要程度、前续知识点、后续知识点和知识点种类等等。测试题所涉及的知识点的重要性对学生是否正掌握该知识点有着重要影响。在FuzzyCDF模型中，学生对知识点的掌握情况，由学生的潜在特质，知识点的区分度和知识点的难度确定，并没有考虑其重要性的影响，因此本研究引入了知识点重要性这个影响因子。已有研究中表明知识点的重要程度与其后继知识点的个数以及相关的试题数量有关，即某知识点被其他知识点用的次数越多，该知识点就越重要。试题库中关于该知识点的试题越多，该知识点越重要[19]。由于本研究的数据没有知识点与后继知识点的关系信息，因此用试题库中知识点出现的次数即知识点出现的频率来表示知识点的重要性，用参数e表示，e=n/m，其中n表示知识点在测试题中出现的次数，m表示测试题的个数。如表1所示，知识点a的重要性为3/8，知识点d的重要性为5/8，由此可知点d的重要性大于点a。

一般情况下，人们认为知识点的重要性和其难度相关[20]。因此，知识点的重要性和难度对其掌握有着类似的影响，基于项目反应理论，可定义知识点的掌握程度为

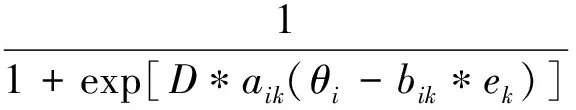
(10)

式中：ek为知识点k的重要性。

表1 测试题考查知识点的出现频率

Tab.1 Frequency of each knowledge point contained in the test

知识点a知识点b知识点c知识点d知识点e测试题100010测试题211101测试题310011测试题401101测试题501010测试题600010测试题711000测试题800010知识点出现频率34253

2.1.2 假设2

在FuzzyCDF模型的主观题假设中，认为学生是否掌握题目属于补偿型。补偿是指学生在某个知识点上的高水平掌握或拥有，可以补偿学生在其他知识点上的低水平掌握或者缺失。在极端情况下，可以认为学生只要掌握一个知识点就会有较高的正确作答概率[21]。因此FuzzyCDF模型在主观题的诊断中假设学生掌握测试题所考查的其中一个知识点就可能答对该测试题。但实际中并非如此。图3给出了人教版小学五年级分数加减法的一道主观题，该题是一道计算题，考查了通分、同分母加减和化简3个知识点。如果学生只掌握了化简这个知识点，那么学生明显无法正确解题。补偿的另一种情况为：学生掌握部分和全部知识正确作答的概率比没掌握任何知识点的概率高[22]，也就是说学生掌握部分知识点也可能正确作答。

因此，本研究假设：随着学生掌握知识点的个数增多，学生正确作答的概率将增高，将学生i掌握主观题测试题j的程度ηij重新定义为

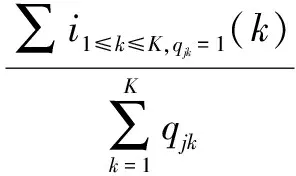
(11)

式中：ηij表示为学生i对测试题j的掌握程度，取值范围为[0,1]，0表示学生i没有掌握测试题j，1表示学生i掌握了测试题j，0～1表示学生i对测试题j的掌握程度；i(k)为学生i对知识点k的掌握程度；qjk=1表示测试题j考查了知识点k；∑i1≤k≤K,qjk=1(k)为学生i对测试题j所涉及到的所有知识点的掌握程度的和，分母表示测试题j所考查的知识点的数量。

图3 主观题答题过程Fig.3 Process of solving a subjective problem

2.2 模型介绍

本研究在FuzzyCDF模型的基础上，基于以上两个假设提出R-FuzzyCDF模型，该模型在一定程度上弥补了FuzzyCDF对主观题诊断的不足。与FuzzyCDF相同，R-FuzzyCDF模型中学生i对测试题j的正确作答概率的计算公式为式(3,4)。

图4所示为R-FuzzyCDF模型的框架示意图，首先将矩阵Q和得分矩阵X输入，通过2.3节中的MCMC算法进行参数估计，利用式(19-22)得到困难度a、区分度b、潜在特质θ、猜测率g、失误率s和主观题归一化方差σ等参数，同时通过矩阵Q计算出知识点重要性e。得到以上参数后，通过式(10)计算得到学生对知识点的掌握情况，再通过式(6，11)计算得到学生对知识点的掌握程度与矩阵Q计算得到学生对测试题的掌握情况，最后通过式(3，4)结合猜测率g和失误率s得出学生对测试题的正确作答概率，从而掌握学生对测试题的得分情况。

图4 R-FuzzyCDF模型框架示意图Fig.4 Schematic diagram of R-FuzzyCDF

2.3 MCMC估计算法

在认知诊断模型中常用的参数估计方法有最大期望(Expectation maximization，EM)算法和马尔可夫链蒙特卡罗(Markov chain Monte Carlo，MCMC)算法。MCMC算法更加适用于多参数的参数估计，因此本研究采用文献[9]提出的MCMC算法进行参数估计。MCMC算法采用吉布斯内的M-H采样法，首先基于Gibbs采样法对未知参数的后验分布进行分解[23]，然后应用M-H算法对区失误率s、猜测参数g、潜在特质θ、主观题归一化方差σ、分度a和困难度b[24]等参数进行估计。

以未知参数的联合后验分布为目标分布，给出模型的联合似然函数为

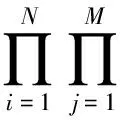
(12)

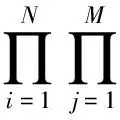
(13)

以上所有参数的联合后验分布为

p(a,b,θ,s,g,σ2|X)∝p(X|a,b,θ,s,g,σ2)P(a,b,θ,s,g,σ2)∝

p(X|a,b,θ,s,g)P(a)P(b)P(θ)P(s)P(g)P(σ2)

(14)

在给定矩阵Q、得分矩阵X和其他参数的条件下，各个参数的全条件分布为

p(a,b|X,θ,s,g,σ2)∝L(s,g,θ,a,b,σ2)P(a)P(b)

(15)

p(θ|X,a,b,s,g,σ2)∝L(s,g,θ,a,b,σ2)P(θ)

(16)

p(s,g|X,a,b,θ,σ2)∝L(s,g,θ,a,b,σ2)P(s)P(g)

(17)

p(σ2|X,s,g,θ,a,b)∝L(s,g,θ,a,b,σ2)P(σ2)

(18)

每个参数的先验分布表示如下

a～logN(0,1),b～N(0,1)

s～4-Beta(1,2,0,0.6),g～4-Beta(1,2,0,0.6)

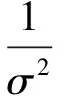
从各参数的全条件分布进行M-H抽样，分别对区分度a、困难度b、失误率s、猜测参数g、潜在特质θ和主观题归一化方差σ进行抽样，参数的抽样过程如下。

(1)a，b参数

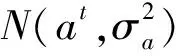
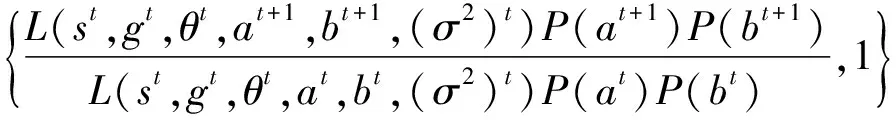
(19)

(2)θ参数

θt参数从正态分布N(θt,σ2)中随机抽取，其θt向θt+1转移的概率计算公式为

(20)

(3)s，g参数

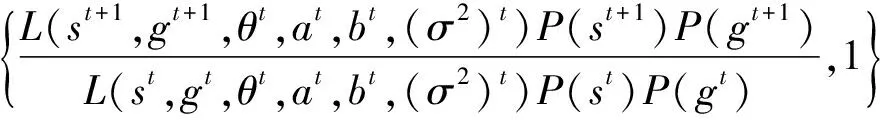
(21)

(4)σ参数

(σ2)t参数从伽马分布U(((σ2)t+1-δσ,((σ2)t+1+δσ)))中随机抽取，(σ2)t向 (σ2)t+1转移的概率计算公式为

(22)

各个参数在抽样后再将其计算概率与r～U(0，1) 产生的随机数进行比较，如果大于等于r，则接受转移，否则不接受转移。

3 实验验证

3.1 实验数据

实验数据分为3个数据集，来自于参考文献[14]，分别是FrcSub数据集，Math1数据集和Math2数据集。FrcSub是关于小学分数加减法测试的数据，测试题只包含客观题[25]；Math1和Math2为某期末数学考试数据，测试题包括客观题和主观题。表2所示为3个数据集的统计情况；图5所示为数据集预览情况，3个数据集都包含矩阵Q和得分矩阵X两个数据。矩阵Q每一列代表一个知识点，每行代表一道测试题，0表示测试题没有考核该知识点，1表示测试题考核该知识点。得分矩阵X每列代表测试题的得分，每行代表一道测试题，得分矩阵X中客观题是0,1矩阵，0表示学生在该题上得分为0，1表示学生在该题上得分为1；而主观题的值为0～1，为主观题得分归一化以后的值。

表2 数据集统计

Tab.2 Dataset statistics

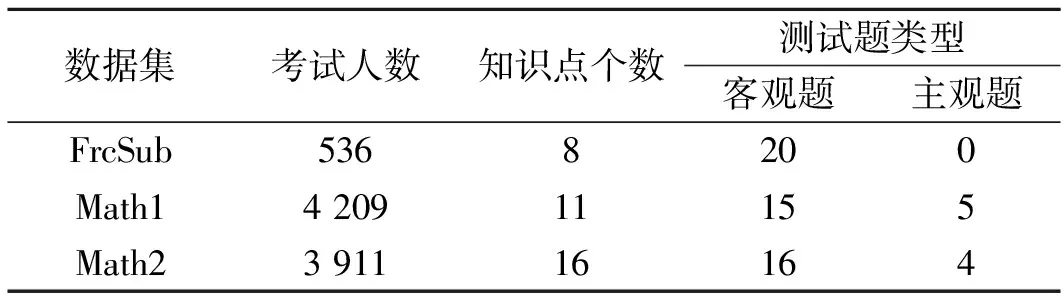
数据集考试人数知识点个数测试题类型客观题主观题FrcSub5368200Math1420911155Math2391116164

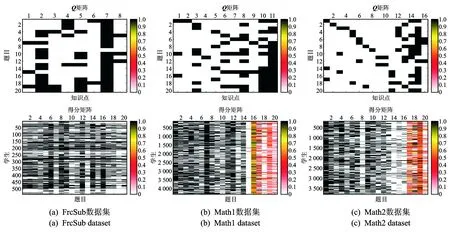
图5 数据集预览Fig.5 Preview of the datasets

3.2 实验方案

教育类模型的评价指标包括模型拟合度、模型精度、模型内外效度和模型的可解释度[26]，其中认知诊断模型的评价指标包括边际判准率、模式判准率和参数的检验误差等。但是以上的评价指标都需要掌握学生对知识点的真实掌握情况，而本研究并不包含该数据，因此本研究采用文献[14]中的实验方案，通过一种间接的方式来评判模型的优劣，即用学生得分的预测准确率作为评价指标。通过这种间接的方法来进行验证，将学生做题的得分数据分成训练集和测试集，通过训练集来训练参数从而得到学生对知识点的掌握情况，然后利用学生对知识点的掌握情况对学生得分进行预测，再与测试集进行比较，计算预测得分与真实得分之间的标准差(RMSE)和平均绝对误差(MAE)，这两个指标越小就说明实验效果越好，说明对学生对知识点掌握情况的诊断越正确。

3.3 实验结果

本研究采用的验证方法是留一交叉验证，即在n道测试题中取n-1道测试题作为训练集来做参数估计从而预测所有学生得分情况，留1道测试题做验证，总共进行n次试验，以保证每道题都验证到，然后计算每道测试题的真实值与预测值的标准差(RMSE)和平均绝对误差(MAE)来作为实验的评价指标，指标越小表明模型越好。计算公式为式(23,24)；并与DINA模型和FuzzyCDF模型进行比较

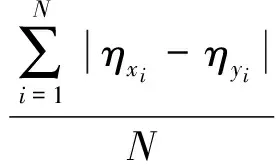
(23)

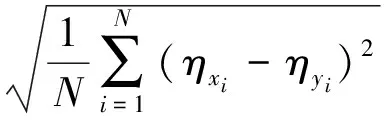
(24)

式中：N表示考试总人数，ηxi表示预测学生i对测试题的得分，ηyi表示学生i的真实得分。

表3～5所示为留一交叉验证的平均结果；图6所示为留一交叉验证每次结果对比；图7所示为假设1：20次的实验结果。R-FuzzyCDF_1只表示引入了假设1；R-FuzzyCDF_2只表示引入了假设2，即主观题的假设的实验结果；R-FuzzyCDF表示同时引入了假设1和假设2的实验结果。

表3FrcSub数据集实验结果

Tab.3ExperimentalresultsonFrcSubdataset

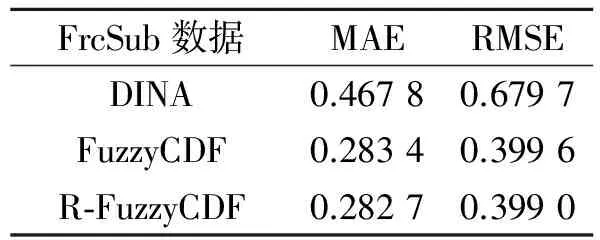
FrcSub数据MAERMSEDINA0．46780．6797FuzzyCDF0．28340．3996R⁃FuzzyCDF0．28270．3990

表4Math1数据集实验结果
Tab.4ExperimentalresultsonMath1dataset

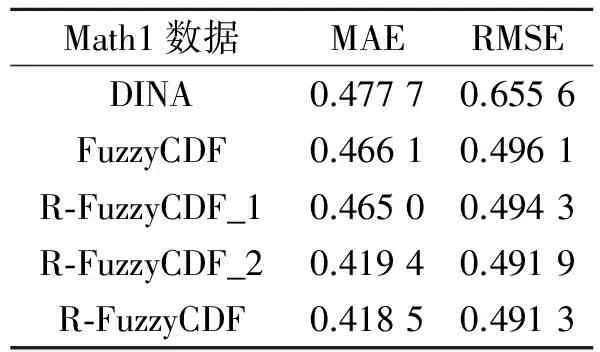
Math1数据MAERMSEDINA0．47770．6556FuzzyCDF0．46610．4961R⁃FuzzyCDF＿10．46500．4943R⁃FuzzyCDF＿20．41940．4919R⁃FuzzyCDF0．41850．4913

表5Math2数据集实验结果
Tab.5ExperimentalresultsonMath2dataset

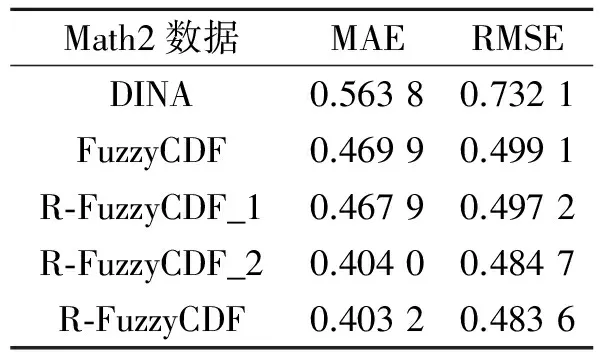
Math2数据MAERMSEDINA0．56380．7321FuzzyCDF0．46990．4991R⁃FuzzyCDF＿10．46790．4972R⁃FuzzyCDF＿20．40400．4847R⁃FuzzyCDF0．40320．4836

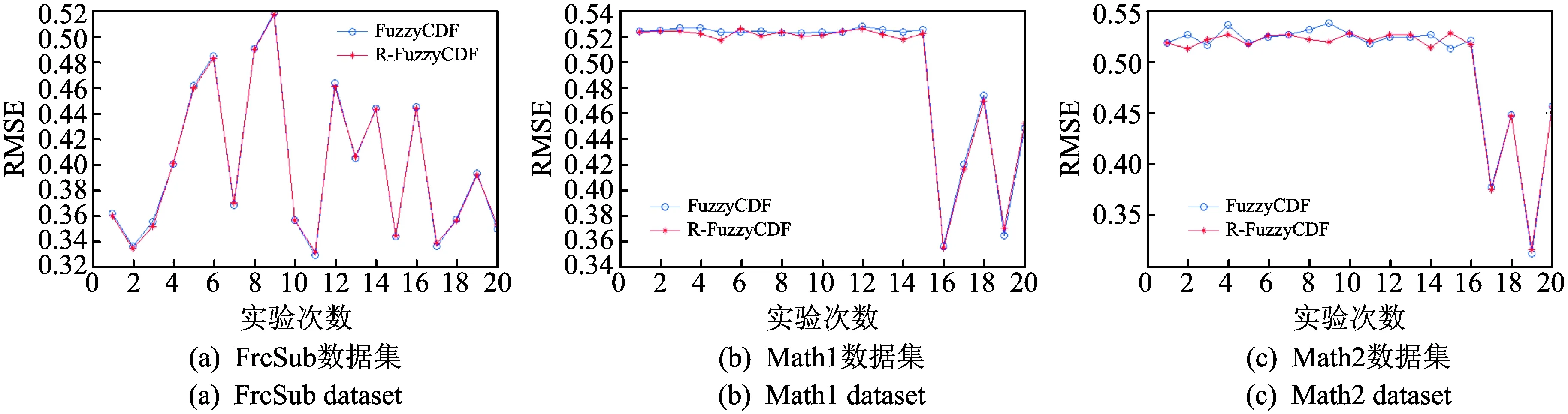
图7 知识点重要性的实验结果Fig.7 Experimental results on the importance of knowledge points

表3～5所示为留一交叉验证的平均结果，3个数据集都考查了20道测试题，也就是分别进行了20次实验。在FrcSub数据集上，因为该数据集只包含客观题，因此针对该数据集，只添加了假设1，R-FuzzyCDF模型与DINA模型相比平均绝对误差低了0.185 1，标准误差低了0.280 7；与FuzzyCDF相比平均绝对误差低了0.000 7，标准误差低了0.000 6，可以认为持平。在Math1数据集上，R-FuzzyCDF模型与DINA模型相比平均绝对误差低了0.059 2，标准误差低了0.164 3；与FuzzyCDF模型相比平均绝对误差低了0.047 6，标准误差低了0.004 8；R-FuzzyCDF_1模型与FuzzyCDF模型相比平均绝对误差低了0.001 1，标准误差低了0.001 9；R-FuzzyCDF_2模型与FuzzyCDF模型相比平均绝对误差低了0.046 7，标准误差低了0.004 2。在Math2数据集上，R-FuzzyCDF模型与DINA模型相比平均绝对误差低了0.160 6，标准误差低了0.248 5；与FuzzyCDF模型相比平均绝对误差低了0.066 7，标准误差低了0.015 5；R-FuzzyCDF_1模型与FuzzyCDF模型相比平均绝对误差低了0.002 0，标准误差低了0.001 9；R-FuzzyCDF_2模型与FuzzyCDF模型相比平均绝对误差低了0.065 9，标准误差低了0.014 4。

图6所示为3个数据集在每道题上的结果曲线图，在FrcSub数据集上，这20道题上R-FuzzyCDF模型相比DINA模型其诊断准确率每次都有明显的提高，但相比FuzzyCDF模型诊断准确率提高不明显；在Math1和Math2两个数据集上，在这20道题上相比DINA模型和FuzzyCDF模型，R-FuzzyCDF模型虽然有波动，但可以看出诊断准确率有了明显提升。从图6中的Math1和Math2的实验结果还可以看出：R-FuzzyCDF模型对主观题有着更准确的诊断。图7为只引入了假设2在20道题上的实验结果，通过这20次实验结果可以看出引入知识点重要性在客观题上的效果较为明显。

4 结束语

本研究在FuzzyCDF的基础上提出了R-FuzzyCDF，引入了知识点重要性和知识点难度对知识点的掌握有着类似的影响及学生掌握的知识点越多得分概率就越大这两个假设。首先通过理论分析表明了两个假设的合理性，然后通过实验进行了验证。实验结果表明：(1)R-FuzzyCDF模型中引入假设1可以有效提高学生对知识点掌握度程度的估计，从而提高学生对测试题得分预测的准确率；(2)在引入假设2后，R-FuzzyCDF模型比其他两个模型表现出明显的提升，同时对主观题的诊断效果有更为明显的提升。(3)综合两个假设后，R-FuzzyCDF模型可进一步提升认知诊断的准确率。

[1] Jang E E. A review of ″Cognitive diagnostic assessment for education: theory and application″[J]. International Journal of Testing, 2008, 8(3):290-295.

[2] Harmelen M V, Workman D. Analytics for learning and teaching[J]. CETIS Analytics Series, 2012, 1(3): 1-40.

[3] Raju P S, Lonial S C, Mangold W G, et al. Differential effects of subjective knowledge, objective knowledge, and usage experience on decision making: An exploratory investigation[J]. Journal of Consumer Psychology, 1995, 4(2): 153-180.

[4] Leighton J P, Gierl M J. Cognitive diagnostic assessment for education: Theory and applications[J]. Journal of Qingdao Technical College, 2007, 45(4):407-411.

[5] Fischer G H. The linear logistic model as an instrument in educational research[J]. Acta Psychologica,1973, 37(6): 359-374.

[6] Tatsuoka K K. Rule space:An approach for dealing with misconceptions based on item response theory[J]. Journal of Educational Measurement, 1983, 20(4): 345-354.

[7] Leighton J P, Gierl J M,Hunka S M. The attribute hierarchy method for cognitive assessment:A variation on Tstsuoka′s rule-space approach[J]. Journal of Educational Measurement, 2004, 41(3): 205-236.

[8] Hartz S M. A Bayesian framework for the unified model for assessing cognitive abilities:Blending theory with practicality[J].American Journal of Gastroenterology, 2002, 95(4): 906-909.

[9] Torre J D L, Douglas J A. Higher-order latent trait models for cognitive diagnosis[J]. Psychometrika, 2004, 69(3): 333-353.

[10] 钱锦昕, 余嘉元. 认知诊断中基于神经网络的PSP方法[J]. 心理科学, 2010(4):915-917.

Qian Jinxin, Yu Jiayuan. The neural network-based PSP method in cognitive diagnosis[J]. Psychological Science, 2010(4):915-917.

[11] 康春花,任平,曾平飞,等. 多级评分聚类诊断法的影响因素[J].心理学报,2016, 48(7): 891-902.

Kang Chunhua, Ren Ping, Zeng Pingfei, et al. The influence factors of grade response cluster diagnostic method[J]. Acta Psychologica Sinica, 2016,48(7): 891-902.

[12] 祝玉芳, 王黎华, 丁树良,等. 多策略的多级评分认知诊断方法的开发[J]. 江西师范大学学报(自然科学版),2015, 39(4): 271-276.

Zhu Yufang, Wang Lihua, Ding Shuliang, et al.The development of multiple-strategies cognitive diagnosis with polytomous response[J]. Journal of Jiangxi Normal University(Natural science), 2015, 39(4): 271-276.

[13] 宋丽红, 戴海琦,汪文义, 等.R-DINA模型参数估计EM算法准确性检验[J].心理学探新,2012, 32(5): 410-413.

Song Lihong, Dai Haiqi, Wang Wenyi, et al. Assessing the performance of EM Algorithm for parameter estimation of the R-DINA Model[J]. Psychological Explortation, 2012, 32(5): 410-413.

[14] Wu R Z, Liu Q, Chen E H, et al. Cognitive modelling for predicting examinee performance [C]∥ International Joint Conference on Artificial Interlligence.Buenos Aires, Argentina:ACM Press,2015:1017-1024.

[15] Baker F B，Kim S H. Item response theory: Parameter estimation techniques[J]. Journal of the American Statistical Association, 2004, 100(2): 299-305.

[16] Fayers P. Item response theory for psychologists[J]. Quality of Life Research, 2004, 13(3):715-716.

[17] Camilli G. Teachers corner: Origin of the scaling constantd=1.7 in item response theory[J]. Journal of Educational and Behavioral Statistics, 1994, 19(3): 293-295.

[18] DiBello L V, Stout W. Guest editors′ introduction and overview: IRT-based cognitive diagnostic models and related methods[J]. Journal of Educational Measurement, 2007, 44(4): 285-291.

[19] 康健. 以知识点为中心的智能导学系统的研究与实现[D]. 长春：东北师范大学, 2010.

Kang Jian. Research and implenmentation of intelligent tutoring system on the basis of knowledge point [D]. Changchun: Northeast Normal University, 2010.

[20] Cheng Y, Zeng G, Xu W S, et al. Research on the interest mining and cluster grouping based on the knowledge point[C]∥Information Communication and Management. Hertfordshire: ICICM, 2016: 7-12.

[21] Torre J D L, Douglas J A. Model evaluation and multiple strategies in cognitive diagnosis: An analysis of fraction subtraction data[J]. Psychometrika, 2008, 73(4): 595-624.

[22] Hong H, Wang C, Lim Y S, et al. Efficient models for cognitive diagnosis with continuous and mixed-type latent variables[J]. Applied Psychological Measurement, 2014, 39(1): 31-43.

[23] Henson R, Douglas J. Test construction for cognitive diagnosis[J]. Applied Psychological Measurement, 2005, 29(4): 262-277.

[24] Hulin C L, Drasgow F, Parsons C K, et al. Item response theory: Application to psychological measurement[J]. British Journal of Surgery, 2009,96(8):955-955.

[25] DeCarlo L T. On the analysis of fraction subtraction data: The dina model, classification, latent class sizes, and the q-matrix[J]. Applied Psychological Measurement, 2011, 35(1): 8-26.

[26] DiBello L V, Roussos L A, Stout W, et al. A review of cognitively diagnostic assessment and a summary of psychometric models[J]. Handbook of Statistics, 2006, 26(6): 979-1030.

RevisedModelofFuzzyCognitiveDiagnosisFramework

Li Youxi1, Wen Yimin1,2, Yi Xinhe1, Xu Zhi1,2

(1.School of Computer Science and Information Security, Guilin University of Electronic Technology, Guilin, 541004, China;2.Guangxi Key Laboratory of Trusted Software, Guilin University of Electronic Technology, Guilin, 541004, China)

To acquire students′ grasping state of the knowledge points and further predict their scores in future tests, a cognitive diagnosis model is applied to explore students′ talent traits by using their test scores and the relationship between a test topic and its knowledge point. However, the available cognitive diagnosis models generally ignore the influence of the number of knowledge points mastered, the mastery degree of knowledge points and the importance of knowledge points on cognitive diagnosis in subjective questions. So a revised fuzzy cognitive diagnosis framework (FuzzyCDF) model is proposed in this paper, which assumes that the probability of answering correctly increases as the number of knowledge points mastered increases in cognitive diagnosis in subjective questions and takes into consideration the influence of the importance of knowledge points on cognitive diagnosis. Experimental results illustrate that the revised FuzzyCDF model can further improve the accuracy of cognitive diagnosis.

cognitive diagnosis; conjunctive; compensatory; importance of knowledge point; subjective question

国家自然科学基金(61363029，61662014)资助项目；广西区科学研究与技术开发项目(桂科攻14124005-2-1)资助项目；教育部在线教育研究基金(全通教育)课题(2016YB155)资助项目；广西高校图像图形智能处理重点实验室课题(GIIP201505)资助项目。

2017-01-05；

2017-04-27

TP181