基于MOPSO与凸优化算法的稀布圆阵列方向图优化

2017-12-15曹爱华李海林马守磊周建江

数据采集与处理 2017年5期

关键词：布阵旁瓣电平

曹爱华李海林马守磊周建江

(南京航空航天大学电子信息工程学院，南京，210016)

基于MOPSO与凸优化算法的稀布圆阵列方向图优化

曹爱华李海林马守磊周建江

(南京航空航天大学电子信息工程学院，南京，210016)

为了降低稀布阵列的峰值旁瓣电平并抑制稀布阵列的栅瓣,提出了一种多目标粒子群与凸优化相结合的方向图综合算法。该算法将多目标粒子群优化(Multi-objective particles swarm optimization,MOPSO)作为全局搜索器，凸优化算法作为局部搜索器来搜索最优解，优化的变量不仅是阵元的权值，而且还加入了阵元位置这一参数，从而能够提供更多的自由度来控制稀布阵列的性能。基于30阵元的稀布圆形阵列的仿真结果表明：与单纯使用MOPSO算法相比，本文提出的用MOPSO算法优化阵元位置，凸优化算法优化阵元权值的联合优化算法，得到的栅瓣和峰值旁瓣电平都小于-19.3 dB。

稀布阵列；凸优化；多目标粒子群；栅瓣抑制；峰值旁瓣电平

引言

近年来，圆阵天线在无线移动通信、雷达和飞机导航等多领域得到了广泛的应用，然而阵元数目的多少往往在很大程度上影响天线系统的复杂度和成本。因此，在保证天线系统性能的条件下，尽可能地减少阵元数目成为当前研究的热点。稀布阵列就是在这样的思想下发展起来的。稀布阵列是指阵元间距无规律分布的非等间隔阵列，阵元的位置在一定范围内随机分布[1]。与传统阵列相比，稀布阵列有很多优势，它可以通过增大孔径的尺寸来产生较窄的波束，而在孔径尺寸一定的条件下，可以通过减少阵元数目来降低天线设计成本[2]。然而稀布阵列的缺陷在于通常会产生栅瓣，并且天线阵列的旁瓣电平较高。因此有效抑制栅瓣，降低天线阵列的峰值电平是稀布阵列研究的重中之重。

国内外学者已经在这方面做了很多的研究，解决稀布阵列高旁瓣问题的主要思想可以划分为两大类，即智能优化算法和凸优化算法。文献[3]将方向图综合问题转化为严格凸优化问题，使用凸优化算法进行线性稀布阵列的方向图合成；文献[4]设计加入了最小阵元间距约束，运用粒子群算法进行非均匀稀布阵列的方向图优化；文献[5]将矩阵束(Matrix pencil method,MPM)的思想运用到稀布平面阵列的方向图综合中，通过对所期望的波束进行奇异值分解获得阵元的位置及权值等参数；文献[6]为降低稀布阵的峰值旁瓣电平，提出了在适应度函数中加改进海明窗的方式进行阵元位置的优化；而文献[7,8]分别研究了多目标粒子群算法和遗传算法，在优化权值的基础上进一步优化了阵元的位置，提高了优化的自由度，但是无法保证优化后的阵元位置和权值完全匹配；文献[9-12]将遗传算法和凸优化算法相结合对稀布阵列进行联合优化；文献[13]应用进化算法和粒子群算法来优化三圆环阵列天线的主瓣和旁瓣约束；文献[14]在给定方向图要求的条件下，通过序列凸优化进行稀布阵列阵元数目最小化的研究；文献[15，16]运用对非凸问题的转化来优化稀布阵列，虽在一定程度上改善了方向图综合的性能，但该转化涉及l1范数到l0范数的近似，给问题的求解带来了一定的误差。

上述文献中运用多种不同的思想对稀疏阵列进行方向图综合，目的就为了提高稀疏阵列的性能。考虑到上述研究在应用遗传算法对目标函数进行优化时，往往会陷入局部最优解且算法的初始点难以确定的缺陷，本文提出了多目标粒子群算法(Multi-objective particle swarm optimization, MOPSO)与凸优化相结合的算法,进行稀布阵列的栅瓣抑制并且最大限度地降低峰值旁瓣电平。将MOPSO作为全局搜索器，凸优化作为局部搜索器，最大限度地降低了陷入局部最优解的概率，提高了算法的优化效率。

1 信号模型

考虑一个圆环阵列，半径R=nλ，其中n为一常数，λ为波长。圆环上分布了N个天线阵元，信号模型如图1所示，将圆环的圆心设置为原点，xi为第i个单元的方位角，假设波束指向为(φ0,θ0)，方向图函数可表示为

(1)

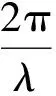
由于这里只考虑圆形阵列所在平面的方向图，则此时θ=90°，可进一步将阵列方向图函数表示为

(2)

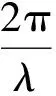
为了形象地描述稀疏阵列的稀疏程度，现定义稀疏阵列的稀疏度为

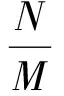
(3)

式中：N为实际排布的阵元数，M为当相邻阵元之间的间距为λ/2时能够排布的阵元数，显然，稀疏度γ表示了阵列稀疏的程度，γ越小，表示稀疏程度越高。

峰值旁瓣电平MSLL定义为

(4)

式中φSL为阵列方向图的旁瓣区域。

为有效减小阵元间的互耦效应，约束相邻阵元的间距不小于某一常量xt，即

min{xi+1-xi}≥xt0≤i≤N-1

(5)

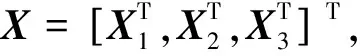
(6)

为使阵元能够较好地分布于整个圆环上，且满足最小间隔限制，人为规定第一个阵元方位角x0=0，最后一个阵元xN-1=2π-xt。

同理，若仅将阵元位置作为优化变量，式(6)的优化模型即可转化为

(7)

2 方向图优化算法

2.1 凸优化算法

凸优化算法指的是目标函数为凸函数且约束条件得到的定义域为凸集的优化问题，其研究的是凸目标函数在许多凸不等式约束、等式约束下的极值问题，它是一类特殊的数学优化问题，属于非线性优化的一个子类。凸优化理论的快速发展归功于其自身的特点，即凸优化问题的局部极小值点都是全局极小值点，并且当凸优化问题为严格凸问题时，其全局极小值唯一。一旦将一个实际的优化模型转化为凸优化问题，则意味着该问题可以得到完美的解决，这是非凸优化问题所不具备的性质。

由上述的信号模型可知，圆阵方向图函数可以表示为

F(φ,θ)=wHb

(8)

其中H代表共轭转置，T代表转置，N为阵元数。

图2 实数域三维二阶锥示意图 Fig．2 Diagram of three-dimensional second-order cone in real number field

因此，可建立圆阵栅瓣抑制优化模型，即

(9)

式中s代表旁瓣区域的离散值。

二阶锥规划是凸优化的一个子集，其标准形式为

minbTx

(10)

图2给出了实数域三维空间二阶锥的示意图，它是一个包含非空内点的尖锐凸集。二阶锥优化即在该尖锐的凸锥集中寻找目标函数的最小值，由图可知，凸集的特性保证了优化问题的收敛性。

式(10)可借助Sedumi工具求解，即

[xs,ys,info]=sedumi(At,bt,ct,K)

(11)

因此，设法将式(9)转换为标准的二阶锥规划形式，以期能够使用Matlab工具箱的Sedumi工具进行高效求解。现考虑将权值拆分为实部wr和虚部wi，同时导向矢量也可拆分为实部和虚部，即

minhTy

(12)

式(12)的优化模型可方便地使用Sedumi工具或CVX工具进行求解。

2.2 多目标粒子群以及凸优化的联合优化算法

粒子群算法(Particle swarm optimization, PSO)是一种有效的全局寻优算法，最早由Kenedy和Eberhart于1995年提出，通过设想模拟鸟群觅食的过程，以解决复杂的优化问题。PSO算法可简述为：设粒子群在一个n维空间内搜索，由N个粒子组成种群X={X1,X2,…,XN}，其中每个粒子所处的位置Xi={xi1,xi2,…,xin}都表示问题的一个解。粒子通过不断调整自己的位置xid来搜索新解，每个粒子都能记住自己搜索到的最优解，记作pid,将整个粒子群经历过的最好的位置，即目前搜索到的最优解，记作pgd。此外每个粒子都有一个速度，记作Vi={vi1,vi2,…,vin}，当两个最优解都找到后，每个粒子分别更新自己的速度和位置，即有

vid(t+1)=wvid(t)+c1rand[pid-xid(t)]+c2rand[pgd-xid(t)]

(13)

xid(t+1)=xid(t)+vid(t+1)

(14)

式中：vid(t+1)表示第i个粒子在t+1次迭代中第d维上的速度，w为惯性权重，c1、c2为加速常数，rand为0～1之间的随机数。此外，为使粒子速度不致过大，可设置速度上限vmax。

MOPSO算法是将Pareto支配和PSO算法结合，粒子的历史最优解和群体最优解相结合，来实现多目标问题求解的一种进化算法。相比于遗传算法[17,18]，MOPSO因其概念简单、易于结合、运行效率高等特点，被广泛应用于解决高维复杂多目标工程优化问题中[19-21]。但由于该算法的局部搜索能力较差，易陷入局部最优解，所得的非劣解集质量往往不佳[22]。而凸优化算法中，任何局部最优解都是全局最优解，并且当该凸问题为严格凸问题时，其全局极值点是唯一的，因此当待求解的问题可以转变为使用凸优化算法求解时，能有效地避免陷入局部最优解。

本文利用MOPSO以及凸优化两种算法的特点，将MOPSO作为全局搜索器，凸优化作为局部搜索器来搜索最优解，凸优化算法能有效地弥补MOPSO算法易陷入局部最优解的缺陷。两种优化算法对稀布阵列进行栅瓣抑制的流程图如图3所示。

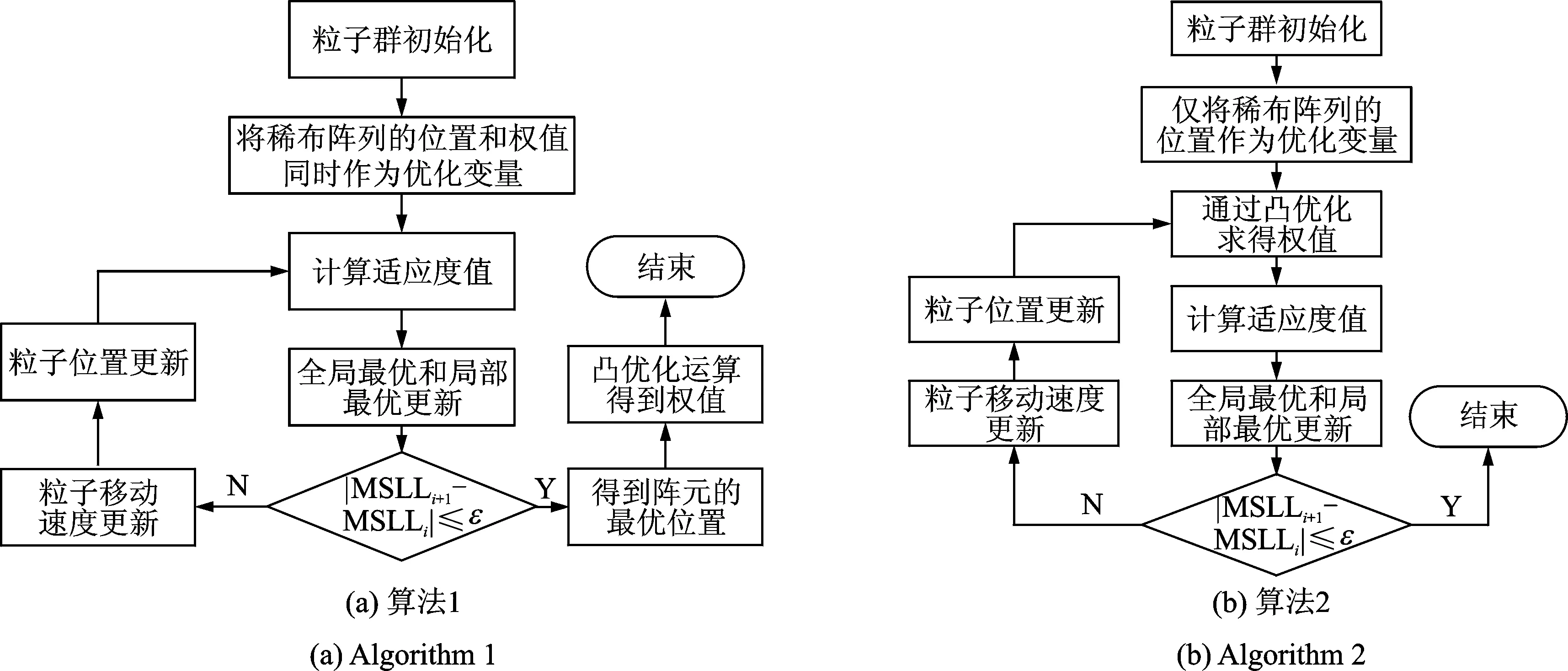
图3 不同优化算法对稀布阵列进行栅瓣抑制的流程图Fig．3 Flow charts of different optimization algorithms on grating lobe suppression of sparse array

算法1的核心思想是利用MOPSO进行位置和权值的联合优化得到一个非劣解，基于非劣解中阵元的位置，采用凸优化算法对阵元权值进行二次优化，得到基于该阵元位置的最优权值信息。算法2中MOPSO只对阵元位置优化，得到每一个粒子的最新位置信息后借助凸优化工具求解阵元的权值进而计算每个粒子的适应度值。该算法的基本思想是将凸优化算法嵌入到MOPSO的代价函数求解中去，保证每次迭代得到的目标函数是基于当前位置的最优值，减少了算法陷入局部极值的可能性，提高了MOPSO算法的优化效率。两种算法的迭代终止条件是：当相邻两次优化所得的峰值旁瓣电平的绝对差值小于某个较小值ε，即|MSLLi+1-MSLLi|≤ε时，可以判断此时算法已达到基本稳定。算法1是在经典MOPSO算法的基础上对优化得到的阵元排布进行了权值的二次优化，仅在最后运用了一次凸优化算法进行权系数的再次优化，该混合算法是将凸优化算法引入方向图栅瓣抑制方法的一种参考方式。而从本文第3节给出的仿真结果可以看出，在使用凸优化算法进行权值的二次优化后，辐射方向图的栅瓣电平有了极大的降低，直观地阐述了凸优化算法在稀布圆阵方向图中的有效性。基于该有效性，促使我们考虑将凸优化算法融入到局部优化中，以期充分利用凸优化的特性得到更优的阵列布局和权系数。为此在算法1的基础上进一步提出算法2，使其对每个粒子都进行凸优化运算，充分利用凸优化的良好特性，从而更好地跳出局部最优解。

3 仿真结果与分析

考虑一个圆形阵列的半径R=5λ，波长λ=0.06 m。令波束指向为(200°,90°)，θ=90°，阵元数N=30，相邻阵元间的方位角最小差值xt=5.73°(距离半波长)，主瓣的带宽为14°，旁瓣的离散化间隔为1°，计算得到该阵列的稀疏度为47.75%。

运用MOPSO算法对圆形阵列模型进行优化，粒子种群数为300，迭代的终止条件为|MSLLi+1-MSLLi|≤0.01。通过仿真迭代计算可知当30个阵元均匀分布于圆环时，使用MOPSO对阵元的权值进行优化，综合所得的方向图仍具有很高的栅瓣，达到-3.747 dB，如图4所示。这表明仅优化稀布阵列的权值不能有效地优化阵列天线的性能，因此考虑提高优化的自由度。

为了进一步提高稀布阵列的性能，对阵元的位置和权值同时进行优化(模型如式(6)所示)，并将凸优化应用于MOPSO中，对权值进行二次优化(优化模型如式(9)所示)，图4显示了用算法1进行仿真的结果，相比于单纯的MOPSO算法，引入凸优化算法后，最大旁瓣电平为-14.35 dB，有了很大程度的改善。本文对于该圆环阵列重点考虑方向图随方位角的变化特性，即只考察该圆环阵列所在平面，因此，下图中均只画出了在俯仰角为90°时阵列的归一化增益随方位角变化的曲线。与文献[8,12]类似，本文在进行圆环阵列的方向图优化时，均只考虑在xy平面内圆环阵列辐射方向图的优化，若需考虑其他方位上的方向图优化，则应当重构阵列优化模型以及阵列方向图的函数表达式。

表1 不同算法优化所得的圆阵峰值旁瓣电平的比较

Tab．1Comparisonofpeakside-lobelevelofthecirculararraywithdifferentalgorithms

算法的类别峰值旁瓣电平/dB均匀阵元间隔的MOPSO-3．747算法1-14．35算法2-19．30

图5为使用算法2对稀布阵列方向图进行优化的结果，在主瓣宽度的约束下，最大旁瓣电平降为-19.3 dB，相比于单独的MOPSO算法以及二次优化算法(算法1)有了很大的改善，这表明对于该圆环阵列模型，所提出的算法2能够找到更优解，从而得到具备更优旁瓣电平性能的稀布阵列。表1列出了不同算法优化后所得到的圆阵峰值旁瓣电平。

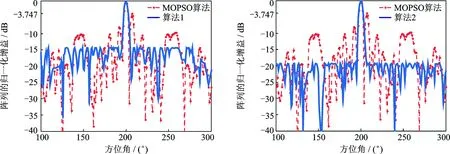
图4 算法1与MOPSO算法比较图5 算法2与MOPSO算法比较Fig．4 Comparison of MOPSO and algorithm 1 Fig．5 Comparison of MOPSO and algorithm 2

表2列出了算法2优化后得到的每个阵元位置(方位角)以及归一化阵元权值的实部和虚部。从表中数据可以看出，此时得到的方位角的精度都很高，但若在实际布阵过程中存在误差，势必会影响方向图综合的效果。为了解决这个问题，可以通过引入阵列流型失配误差，重构稳健的凸优化模型的方式，重新优化得到稳健的阵列布局和权值的最佳组合。该方法已在本文作者的另一篇论文中得到验证。

表2 最优的阵元方位角及权值

Tab．2 Optimal azimuth angles and weights of array elements

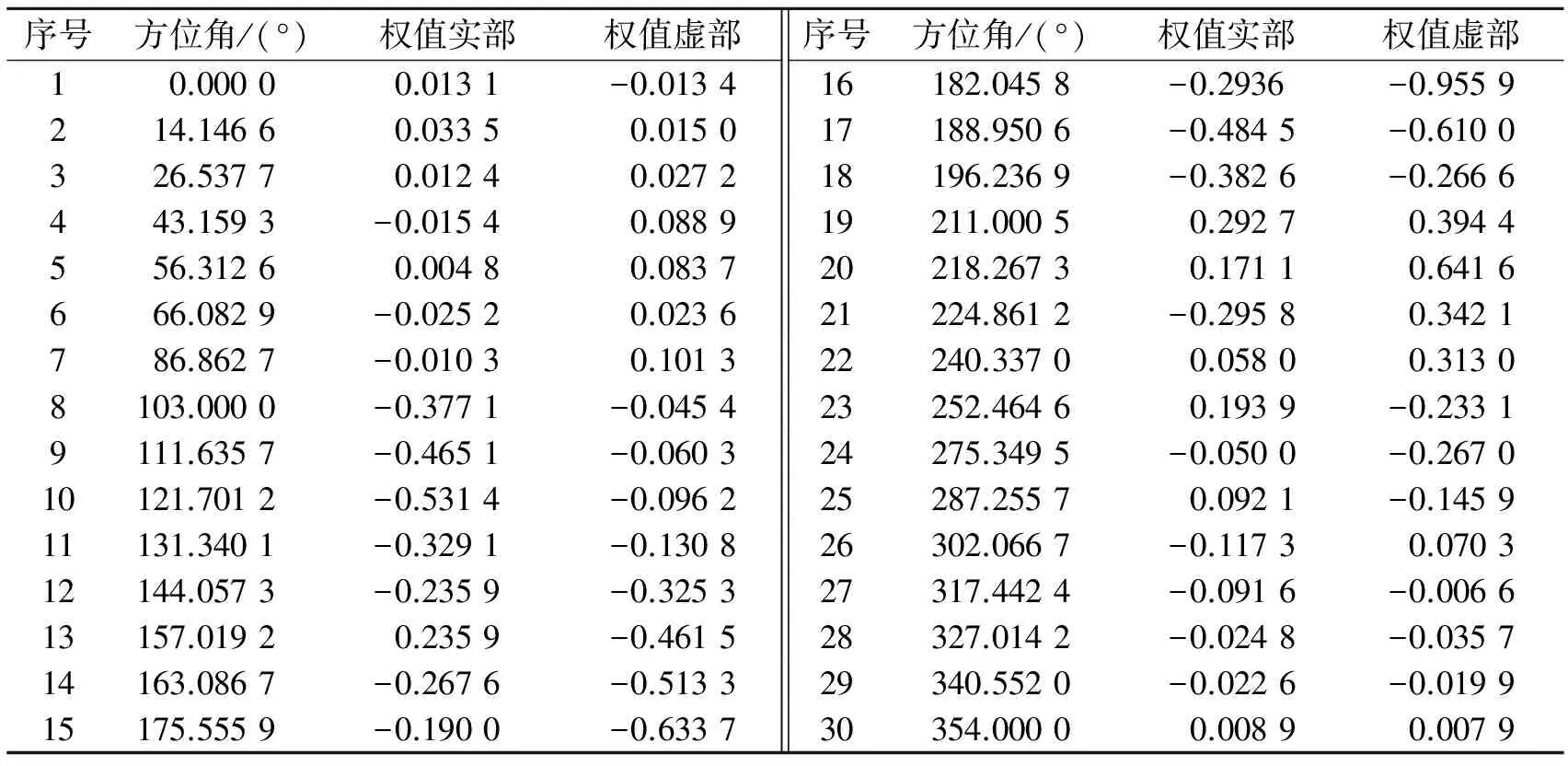
序号方位角/(°)权值实部权值虚部序号方位角/(°)权值实部权值虚部10．00000．0131-0．013416182．0458-0．2936-0．9559214．14660．03350．015017188．9506-0．4845-0．6100326．53770．01240．027218196．2369-0．3826-0．2666443．1593-0．01540．088919211．00050．29270．3944556．31260．00480．083720218．26730．17110．6416666．0829-0．02520．023621224．8612-0．29580．3421786．8627-0．01030．101322240．33700．05800．31308103．0000-0．3771-0．045423252．46460．1939-0．23319111．6357-0．4651-0．060324275．3495-0．0500-0．267010121．7012-0．5314-0．096225287．25570．0921-0．145911131．3401-0．3291-0．130826302．0667-0．11730．070312144．0573-0．2359-0．325327317．4424-0．0916-0．006613157．01920．2359-0．461528327．0142-0．0248-0．035714163．0867-0．2676-0．513329340．5520-0．0226-0．019915175．5559-0．1900-0．633730354．00000．00890．0079

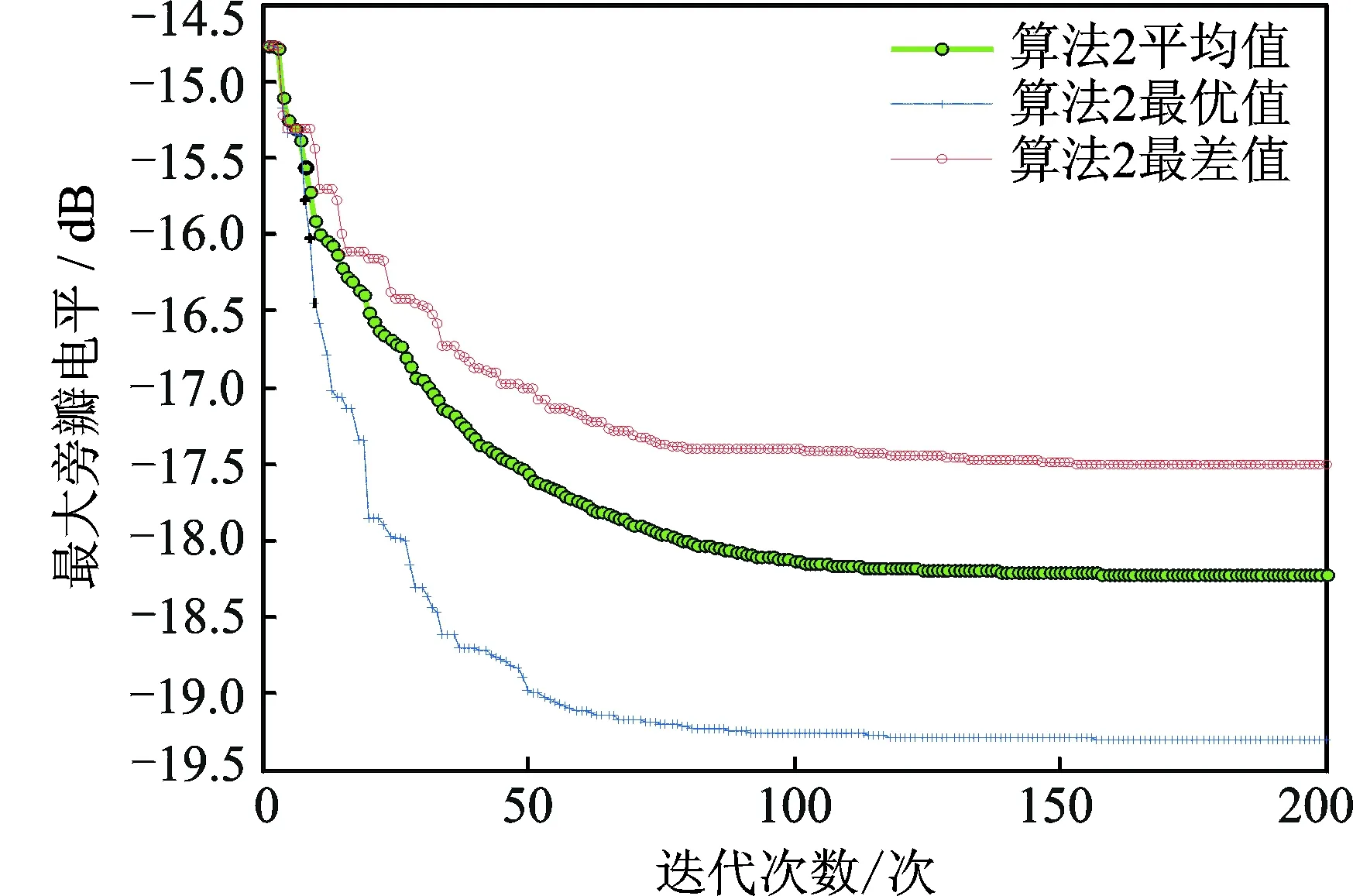
图6 算法2经过20次独立实验的收敛曲线Fig．6 Convergence curve of twenty independent experiments by algorithm 2

为进一步说明算法2的有效性以及稳定性，图6给出了20次独立实验的收敛曲线。根据所设定的迭代终止条件，算法在150次左右达到基本稳定，为更直观地显示该算法的稳定性，图中画出了200次迭代的整体情况。由图可以看出，最差副瓣电平为-17.511 dB，最优副瓣电平为-19.3 dB。

4 结束语

由实验仿真分析可知，当只对阵元进行权值优化时，稀布阵列的栅瓣现象仍然十分严重，因此本文首先考虑将阵元位置和阵元权值作为联合优化变量，扩大了寻优空间的自由度。另外，由于考虑到MOPSO算法在解决高维问题时常常会陷入局部解，而而在凸优化问题中，局部最优解就是全局最优解。因此，引入凸优化算法来弥补多目标粒子群算法的缺陷，本文提出的联合优化算法，充分考虑到两种优化算法的特性，将MOPSO用于全局搜索最优解，而凸优化算法用于局部搜索最优解。仿真结果表明，所提的算法提高了寻优效率和寻优性能。由于本文未对权值的动态范围加以限定，因此权值约束下的方向图综合将是下一步研究的重点。

[1] Toso G, Mangenot C, Roederer A G. Sparse and thinned arrays for multiple beam satellite applications[C]//European Conference on Antennas and Propagation. London, UK:IET,2008: 1-4.

[2] Leeper D G. Isophoric arrays-massively thinned phased arrays with well-controlled sidelobes[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(12): 1825-1835.

[3] Cen L, Ser W, Cen W, et al. Linear sparse array synthesis via convex optimization[C]//IEEE International Symposium on Circuits and Systems. Paris,France:IEEE, 2010: 4233-4236.

[4] 孙绍国. 基于粒子群算法的非均匀稀布阵列综合[J]. 火控雷达技术, 2014, 43(1):14-17.

Sun Shaoguo. Synthesis of non-uniform sparse array based on PSO[J]. Journal of Fire Control Radar Technology， 2014, 43(1):14-17.

[5] Yang K, Zhao Z, Liu Y. Synthesis of sparse planar arrays with matrix pencil method[C]//International Conference on Computational Problem-Solving. [S.l.]:IEEE, 2011: 82-85.

[6] 潘妍妍, 邓维波. 低峰值旁瓣电平稀布阵综合算法研究[J]. 雷达科学与技术, 2013, 11(3):290-294.

Pan Yanyan, Deng Weibo. Study on the optimization algorithm for lower peak side-lobe level of sparse array [J]. Journal of Radar Science and Technology, 2013, 11(3):290-294.

[7] Jin N, Rahmat-Samii Y. Advances in particle swarm optimization for antenna designs: Real-number, binary, single-objective and multi-objective implementations[J]. Antennas & Propagation IEEE Transactions on, 2008, 55(3):556-567.

[8] 黄中瑞, 牛朝阳, 刘春生. 基于改进遗传算法的圆阵列方向图联合优化[J]. 计算机工程, 2013, 39(2):182-186.

Huang Zhongrui, Niu Zhaoyang, Liu Chunsheng. Joint optimization of circular array pattern based on improved genetic algorithm[J]. Journal of Computer Engineering, 2013, 39(2):182-186.

[9] Zhao Yongbo, Huang Jingfang, Zhang Zhaoyang. Synthesis of unequally spaced array by genetic algorithm and convex optimization[C]//Radar Conference, 2009 IET International. [S.l.]:IET, 2009: 1-4.

[10] 何学辉, 吴兆平, 吴顺君. 一种任意阵的方向图模值综合方法[J]. 电子学报, 2010, 38(10):2292-2296.

He Xuehui, Wu Zhaoping, Wu Shunjun. Pattern synthesis with desired magnitude response for arbitrary arrays [J]. Chinese Journal of Electronics, 2010, 38(10):2292-2296.

[11] 黄中瑞, 刘春生, 王珽. 应用遗传算法和序列锥规划进行圆阵的方向图综合[J]. 声学学报, 2014,39(6):696-704.

Huang Zhongrui, Liu Chunsheng, Wang Ting. Pattern synthesis of the circular array using genetic algorithm and sequential cone programming [J]. Acta Acustica, 2014,39(6):696-704.

[12] 袁飞, 杨波, 黄中瑞. 基于凸-改进遗传算法的圆阵列方向图联合优化[J]. 火力与指挥控制, 2015, 39(1):182-186.

Yuan Fei, Yang Bo, Huang Zhongrui. Joint optimization about pattern synthesis of circular arrays based on convex optimization and modified genetic algorithm[J]. Fire Control & Command Control, 2015, 39(1):182-186.

[13] Mandal D, Ghoshal S P, Bhattacharjee A K. Application of evolutionary optimization techniques for finding the optimal set of concentric circular antenna array[J]. Expert Systems with Applications, 2011, 38(4):2942-2950.

[14] Fuchs B. Synthesis of sparse arrays with focused or shaped beampattern via sequential convex optimizations[J]. IEEE Transactions on Antennas & Propagation, 2012, 60(7):3499-3503.

[15] Prisco G, D′Urso M. Maximally sparse arrays via sequential convex optimizations[J]. Antennas and Wireless Propagation Letters, IEEE, 2012, 11: 192-195.

[16] Chen H, Wan Q. Non-uniform array pattern synthesis using reweighted1-norm minimization[J]. AEU-International Journal of Electronics and Communications, 2013, 67(9): 795-798.

[17] Tang J Y，Xie Y L，Peng C C. A dynamic sub-array divided technique for spherical conformalarray antenna using K-means algorithm[J]. Advanced Materials Research，2014，926-930: 2884-2888.

[18] Krivosheev Y V，Shishlov A V，Denisenko V V. Grating lobe suppression in aperiodic phased array antennas composed of periodic subarrays with large element spacing[J]. Antennas & Propagation Magazine IEEE，2015，57(1)：76-85.

[19] 李海林, 周建江, 谭静, 等. 基于 MOPSO 算法的卫星共形阵列天线多波束形成[J]. 数据采集与处理, 2014, 29(3): 415-420.

Li Hailin, Zhou Jianjing, Tan Jing, et al. Multi-beam forming of satellite conformal array antenna based on multi-objective particle swarm optimization[J]. Journal of Data Acquisition and Processing, 2014, 29(3): 415-420.

[20] 储颖，糜华，纪震，等．基于粒子群优化的快速细菌群游算法[J]．数据采集与处理，2010，25(4)：443-448.

Chu Ying, Mi Hua, Ji Zhen, et al. Fast bacterial swarming algorithm based on particle swarm optimization [J]. Journal of Data Acquisition and Processing, 2010，25(4)：443-448.

[21] Wen T L，Xiao W S，Yong Q H，et al. A hybrid optimization algorithm and its application forconformal array pattern synthesis[J]. IEEE Transactions on Antennas & Propagation，2010，58(10)：3401-3406.

[22] 王丽萍, 吴秋花, 邱飞岳,等. 局部搜索与改进MOPSO的混合优化算法及其应用[J]. 计算机科学, 2012, 39(11):174-178.

Wang Liping, Wu Qiuhua, Qiu Feiyue, et al. Hybrid optimized algorithm based on improved MOPSO and local search and its application[J]. Journal of Computer Science, 2012, 39(11):174-178.

SparseCircularArrayPatternOptimizationBasedonMOPSOandConvexOptimization

Cao Aihua, Li Hailin, Ma Shoulei, Zhou Jianjiang

(College of Electronic and Information Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China)

To reduce the peak side-lobe level of the sparse array pattern effectively and suppress the sparse array grating lobe at the same time, a pattern synthesis algorithm using multi-objective particles swarm optimization (MOPSO) combined with convex optimization algorithm is presented in this paper. We take MOPSO as a global search and convex optimization as the local search to search for the optimal solution. In this search, the optimization variables include not only the weights of the array, but also the positions of the array, which can provide more freedom to control the performance of the sparse array. Simulation of a sparse circular array model of thirty elements reveals that compared with MOPSO algorithm alone, the proposed algorithms which uses MOPSO and convex optimization to optimize the positions and the weights of the array respectively, can obtain the grating lobes and the peak side-lobe level of lower than -19.3 dB at the same time.

sparse array; convex optimization; multi-objective particles swarm; grating lobe suppression; peak side-lobe level

国家自然科学基金(61371170)资助项目；南京航空航天大学研究生创新基地(实验室)开放基金(kfjj20150403,kfjj20160404)资助项目；中央高校基本科研业务费专项资金(NJ20140010)资助项目；雷达成像与微波光子技术教育部重点实验室(南京航空航天大学)资助项目。

2015-07-28；

2016-07-11

TN828.5