大规模测评中IRT等值的影响因素研究

曾平飞 李雨秦 刘文惠 焦丽亚 康春花

（1.浙江师范大学教师教育学院，浙江金华 321004；2.合肥晶合集成电路有限公司，合肥 230012；3.教育部考试中心，北京 100084）

大规模测评中IRT等值的影响因素研究

曾平飞1李雨秦1刘文惠2焦丽亚3康春花1

（1.浙江师范大学教师教育学院，浙江金华 321004；2.合肥晶合集成电路有限公司，合肥 230012；3.教育部考试中心，北京 100084）

通过模拟和实证研究探讨样本量、题本量以及锚题题型对大尺度测评中项目参数等值精度的影响，模拟研究和实证研究的结果均表明：（1）0/1计分项目参数的等值精度在大多数条件下均好于多级计分项目，相对而言，实证研究的差异不如模拟研究明显；（2）相对而言，样本容量的增加对于提高项目参数等值精度有着重要的作用，而增加题本数量的作用甚微；（3）无论是区分度参数还是难度参数，均表现为3个题本和2 000人的搭配已经可以达到较好的等值精度，如果进一步提高等值精度，只需将每一题本的样本容量增加到3 000人即可；在多级计分时，当选用5个题本时，每一个题本2 000人是最适宜的组合。

项目反应理论；等值；同时估计；锚测验非等组设计

1 引言

在日益注重教育质量和教育内涵的“互联网+”时代，学生能力国际评价项目（Programme for International Student Assessment，PISA）、国际教育成就评价协会（International Assessment for the Evaluation of Education，IEA）主持的数学与科学学习国际比较研究（The Trends in International Mathematics and Science Study，TIMSS）、美国国家教育进展评估（National Assessment of Education Progress，NAEP）和我国的基础教育质量监测（Basic Education Quality Assessment）等大型测评项目，在世界上的影响越来越大。就教育测量学的技术而言，这些测评项目的一个共同的经验是：在对教育质量进行大范围、广领域的评估或监测时，都应用了大规模教育测评中的矩阵取样技术（matrix-sampling，MS）[1]。MS通过将测验题目的随机平行等份（题本）分配给随机选取的学生来估计测验总分。与传统施测不同，在MS情境下，由于在不同题本上作答的学生样本不同，为了实现对学生能力和题目参数的估计与比较，就涉及题本之间的等值问题。MS可以分为完全矩阵取样和不完全矩阵取样两类，两者主要区别在于不同题本之间是否存在共同题或锚题（common items/anchor items）。不完全矩阵取样的锚题可以帮助解决学生个体间结果的比较问题，为避免锚题在不同题本间的位置效应，目前运用最多的是平衡不完全组块设计（Balanced Incomplete Block Design，BIB），其中锚题为循环锚。循环锚在等值设计中也有应用，如锚题非等组设计（non-equivalent groups with anchor test design，NEAT）。

国内外关于NEAT设计的等值研究主要集中在锚题特征和配置方式上。其中锚题特征主要包括锚题长度、难度、题型等，锚题的配置方式是指题本以何种方式进行链接。在锚测验长度方面，Kolen等建议在相对较长的测验中锚测验需要占20%；张忠华等探讨了共同题数量和测验长度对等值精确性的影响[2]；蔡艳等在NEAT设计下固定测验长度和样本量，探讨了锚题比例对等值精度的影响并讨论了在实际等值中的应用[3]。熊建华等采用模拟研究对IRT等值中锚题长度进行了研究，结果显示，随着测验题量的减少，锚题量需相应增加[4]。在锚测验难度范围方面，Shinharay等通过模拟和实证数据，探讨了3种锚测验（微型锚、midi锚和半midi锚）与总测验原始分的相关，结果表明，midi锚和总测验的相关显著高于微型锚和总测验的相关[5]。Liu等使用SAT实证数据验证midi锚和微型锚的性能，研究表明，midi锚的随机等值误差、总体偏差和RMSE在所有实验情境下都小于或近似于微型锚[6]。在锚测验题型方面，戴海琦等的实证研究证明了在NEAT设计下锚题为纯客观题时的等值结果最好[7]。黎光明等以等值标准误为因变量探讨了全测验与锚测验不同题型分值比对等值误差的影响[8]。在锚测验配置方面，Kolen和Brennan研究指出，链式链接和集中式链接在不同条件下各有优劣[9]。杨涛等利用实测数据证明在多题本共同题设计下，在链式链接中随着链接题本数量的增加，参数的等值精度下降[10]。

已有的研究大多关注两个测验间的等值，但在大规模测评背景下，多题本设计已经成为趋势。我国学者杨涛、辛涛和高燕首次在NEAT设计下，利用实测数据研究了多题本间的等值问题，探讨了等值方法和锚题链接方式对等值效果的影响[10]。然而，对大规模测评的NEAT设计的等值效果同样具有重要影响的测验题型、样本量和题本数量等因素尚未探讨。基于此，本项研究采用在大规模测评中使用较多的NEAT等值设计，考察测验题型、样本量和题本数量对项目参数等值效果的影响，并用实证数据加以验证，以期为我国大规模测评项目的持续推进提供有用的信息。

2 模拟研究

2.1 NEAT等值设计

在NEAT设计中，根据锚题在测验中的配置方式可分为循环锚和中心锚两种形式。相较而言，循环锚题设置在一定程度上包含矩阵取样设计的思想，更加符合大规模测验的情境，因而本项研究选取循环锚作为锚题配置方式，如表1所示。

表1循环锚配置

2.2 变量设定

本项研究主要探讨在NEAT设计下，样本量（1 000人、2 000人、3 000人）、题本数量（3个、5个、7个）和锚题题型（0/1计分、多级计分）3个变量对等值效果的影响。根据3个变量之间不同水平的组合可得到3×3×2=18种实验条件，如表2所示。

2.3 生成模拟数据

NEAT模拟情境如表3所示。根据在以往研究中学者对各参数范围设定的建议，用自编R语句实现模拟数据的生成，再用自编R程序调用Open-BUGS软件进行参数估计，每种条件模拟20次。大体的数据模拟生成步骤如下。

（1）能力参数的产生：分别产生18种条件下服从N（0，1）分布的能力值，范围界定于（-3～3）。

（2）项目参数的产生：分别产生符合18种条件的项目参数，项目参数设定如下：区分度参数服从lognormal（1.13，0.6）分布，并将其范围界定于（0.5～2.5）。难度参数服从N（0，1）分布，同时将其范围界定于（-3～3）。

（3）被试作答反应的生成：利用等级反应模型（GRM）计算被试的正确作答概率，并和随机数进行比较。

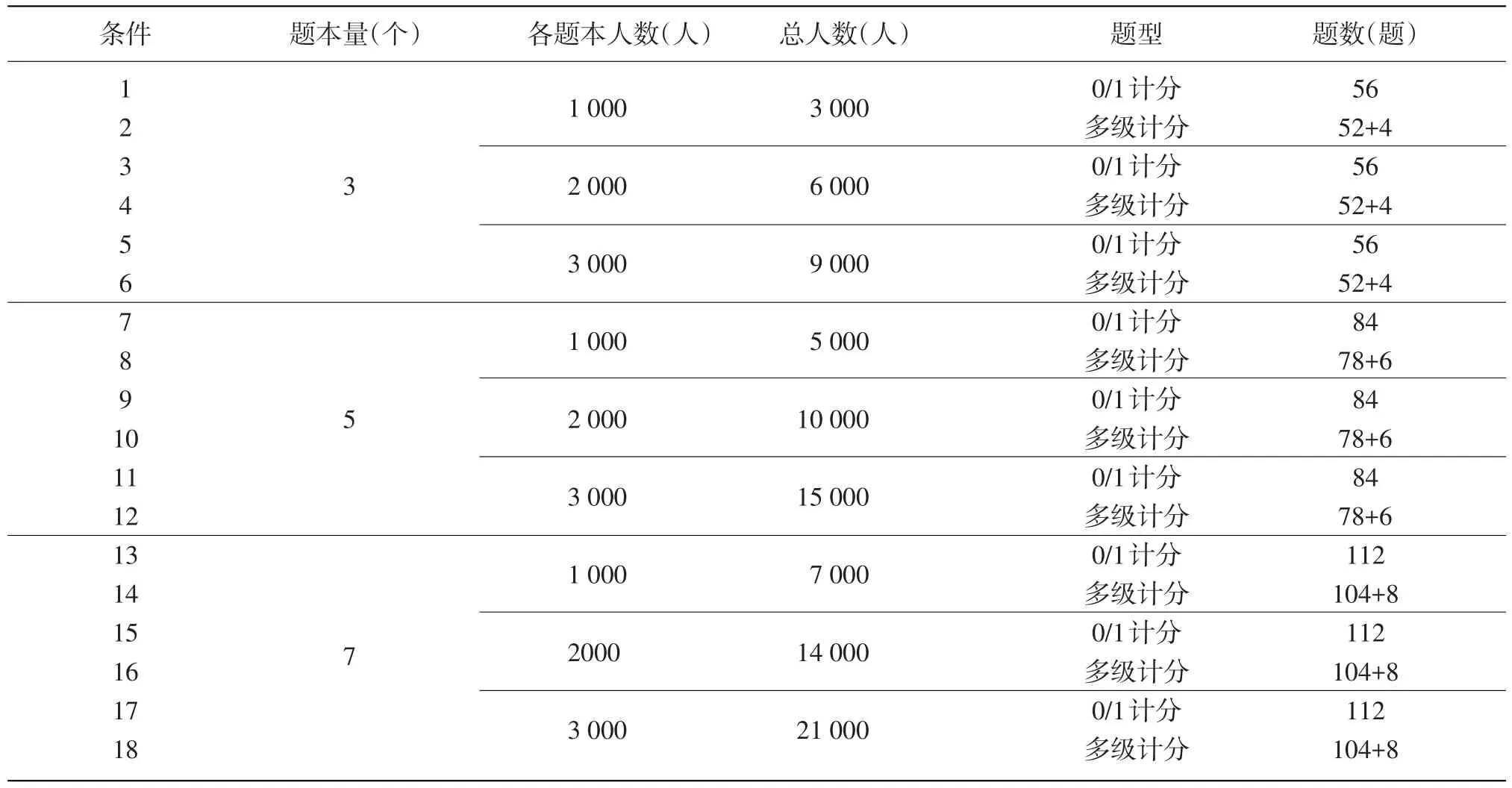
表2变量设定

表3 NEAT模拟情境

2.4 模拟研究指标

根据以往研究，选用误差均方根（RMSE）作为模拟研究的评价指标[11]。

误差均方根公式如下：

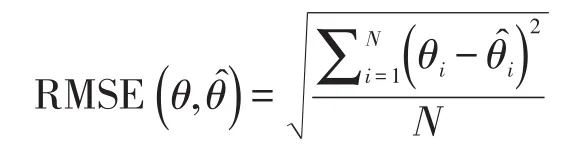
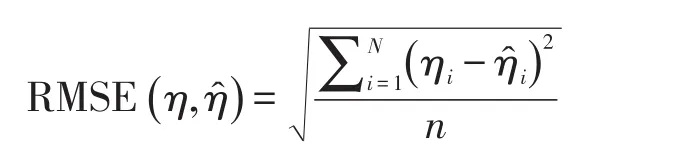
其中，N表示被试人数；表示被试能力真值；表示被试能力估计值；n表示试题数；表示项目参数真值；表示项目参数估计值。

2.5 结果

2.5.1 各因素对区分度参数等值精度的影响

区分度参数的等值RMSE如表4所示。

由表4可知，各个条件下的等值RMSE均在0.40以下，其中0/1计分项目的RMSE值范围在0.1444～0.2171；多级计分项目的RMSE值范围在0.2725～0.3923。不同条件下区分度参数等值的RMSE变化趋势见图1。

从图1可以看出，总体而言，无论在何种样本容量及何种题本数量下，0/1计分项目的区分度等值精度都要好于多级计分项目。具体而言，0/1计分时，区分度等值的RMSE随着样本容量的增加而降低，然而在某一固定样本容量内部，区分度在各题本时的等值精度并无差异。也就是说，在0/1计分时，要提高区分度等值精度，只有增加每一题本内的样本容量，增加题本数目并不能起到显著作用。但在多级计分情况下，3 000人时，题本数量为3个和7个时，等值精度最好，1 000人和2 000人时，题本数量之间并无多大差异，3个题本也能达到与5个和7个同样的等值精度。当选用5个题本时，选择2 000人较为适宜。

表4区分度参数的等值RMSE

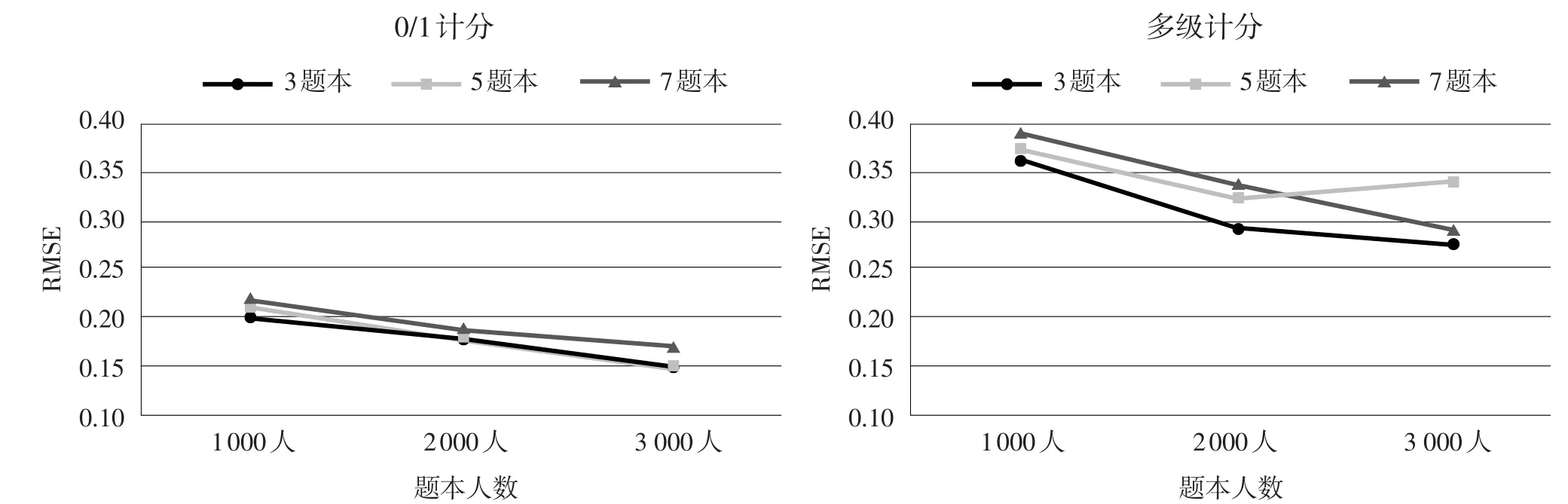
图1不同条件下区分度参数等值的RMSE变化趋势

2.5.2 各因素对难度参数等值精度的影响

难度参数的等值RMSE如表5所示。

由表5可知，各个条件下的等值RMSE均在0.48以下，其中0/1计分项目的RMSE值范围在0.1470～0.1870；多级计分项目的RMSE值范围在0.2551～0.4753。不同条件下难度参数等值的RMSE变化趋势见图2。

从图2可以看出，与区分度参数一样，总体而言，无论在何种样本容量及何种题本数量下，0/1计分项目的难度参数等值精度都要好于多级计分项目。具体而言，在0/1计分时，与区分度参数一致，难度参数的等值精度在各题本间并无显著差异，而在样本容量的变化趋势上却略有不同，相对而言，并不是样本容量越大越好，而是2 000人比1 000人和3 000人要稍好。换句话说，在0/1计分时，要提高难度参数等值精度，在3个、5个、7个题本时，只需2 000人即可。就多级计分而言，难度参数等值精度的变化趋势与区分度参数等值精度的变化趋势不同。难度参数等值精度大体呈现随样本容量增大而提高的趋势，即无论何种题本数量，均为 3 000人时，精度最高，且题本数量之间并无显著差异。此外，当1 000人和2 000人时，3个题本的等值精度明显好于5个和7个题本，尤其以2 000人时较为明显。也就是说，在多级计分时，较少的题本量和每一题本内较适中的样本容量即可达到较好的难度参数等值效果，要达到最好的等值效果，也只需将样本容量继续增加到3 000人即可，而无需增大题本量。

表5难度参数的等值RMSE

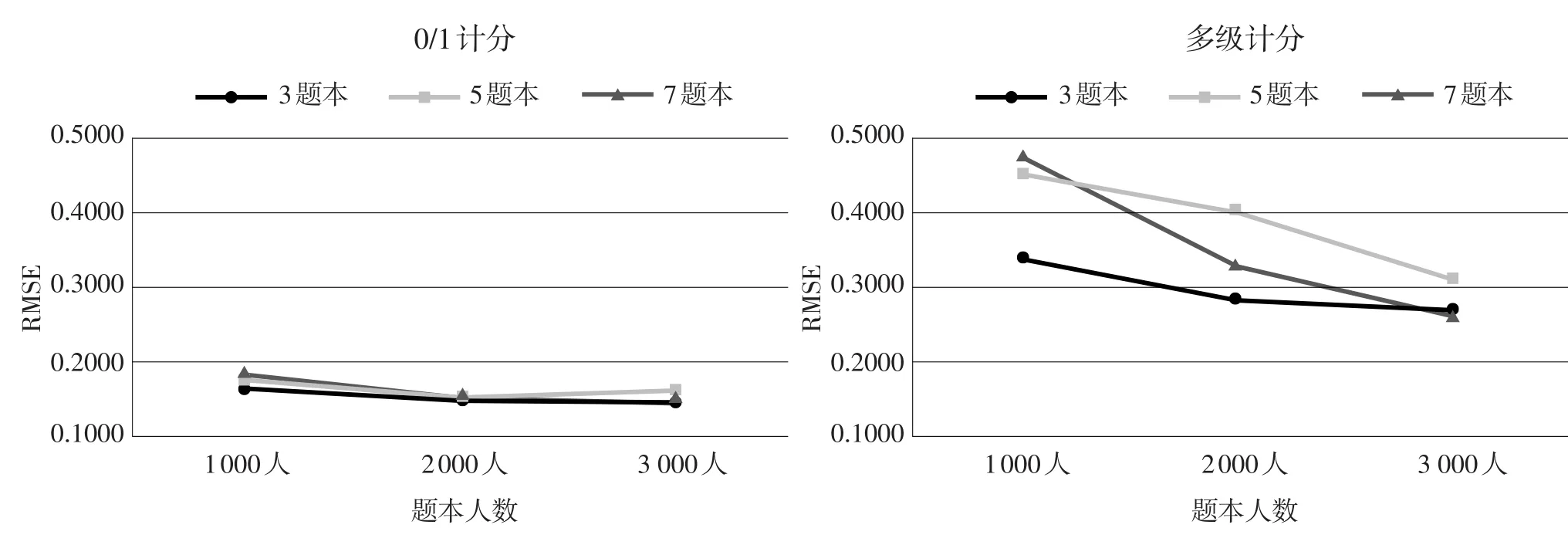
图2不同条件下难度参数等值的RMSE变化趋势

3 实证研究

3.1 研究目的

探查各模拟情境在实际测验情境中的适用情况，进一步验证模拟研究的结果。

3.2 数据来源

实证研究采用2011年TIMSS八年级学生科学成绩数据。对TIMSS的数据进行清理，实证数据结构符合模拟研究中的各项条件。

3.3 研究设计

3.3.1 等值设计

等值设计为NEAT设计，具体同模拟研究，锚题为循环锚配置。

3.3.2 研究工具

实证研究工具与模拟研究中保持一致，同样采用R软件自编程序调用OpenBUGS软件进行参数估计，最后计算等值估计误差并使用SPSS18.0中文版软件进行各题本的描述性统计检验。

3.3.3 评价指标

实证研究采用杨涛等在研究大规模测评多题本等值时使用的指标[10]。这个指标是一种交叉验证（cross validation）的分析方法：以每种等值方法本身的大样本等值效果为标准，从大样本中随机抽取10%的样本量作为小样本，等值精度通过小样本估计的各参数和通过大样本估计的各参数间的差距大小来衡量。其计算公式为:

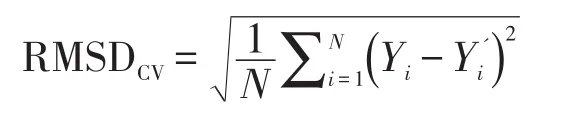
其中，CV表示交叉验证，N表示待等值题本中的题目数量，Yi是通过小样本估计的各参数，Y'i为依据大样本估计的各参数。

3.4 结果

3.4.1 不同题本的基本统计结果

从表6可以看出，在第一个条件中3个题本的总平均分接近，初步说明3个题本的难度相近。另外，3个题本的α系数都在0.75以上，信度较高，并且其信度值也大体相近，满足等值等信度的要求。限于篇幅，此处仅列举条件1题本数据的描述性统计，其他条件均符合要求。

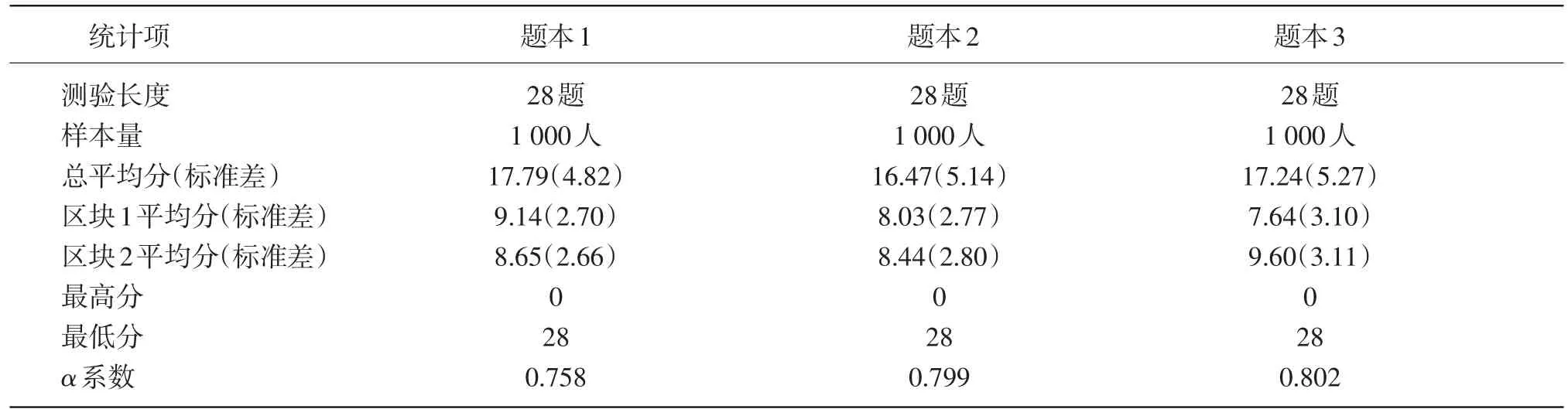
表6 1 000人3题本0/1计分数据的描述性统计表

表7区分度参数的RMSD

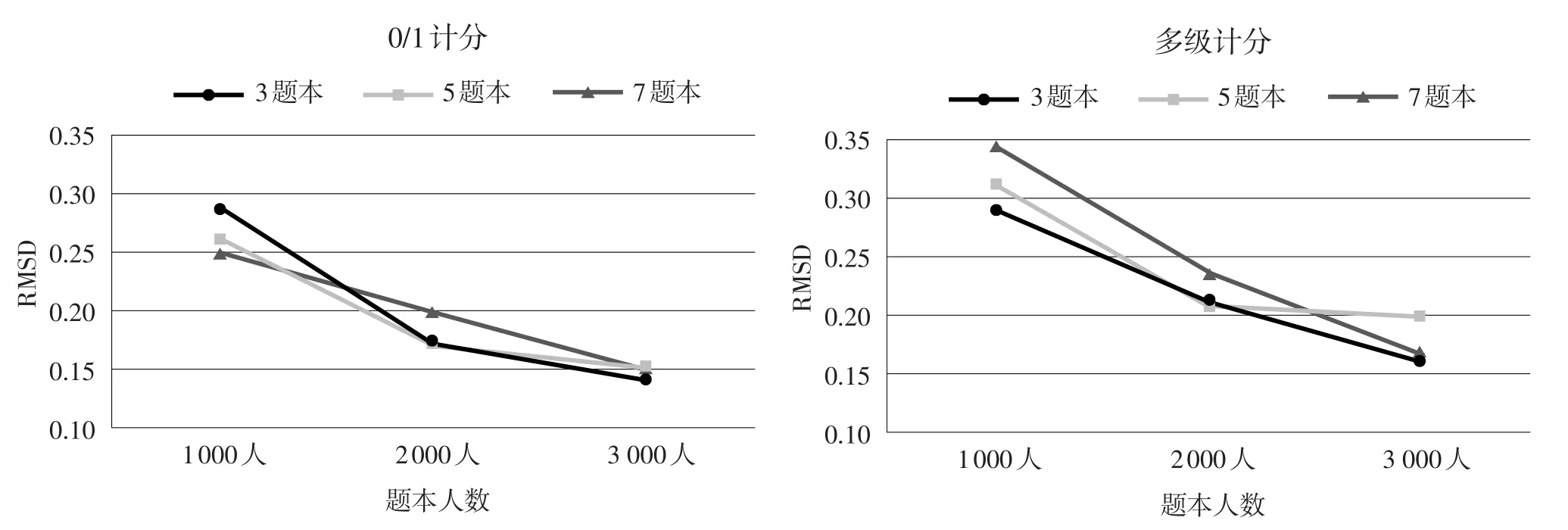
图3不同条件下区分度参数等值的RMSD变化趋势

3.4.2 区分度参数的RMSD

区分度参数的RMSD如表7所示。

由表7可知，各个条件下的RMSD均在0.35以下，其中0/1计分项目的RMSD范围在0.1371～0.2869；多级计分项目的RMSD范围在0.1581～0.3488。不同条件下区分度参数等值的RMSD变化趋势见图3。

从图3可以看出，总体而言，无论在何种样本容量及何种题本数量下，0/1计分项目的区分度参数等值精度都要好于多级计分项目，然而，其差异程度并不如模拟研究结果明显。具体而言，0/1计分项目的区分度等值精度的变化趋势与模拟研究类似，并且随样本容量的变化较模拟研究结果明显，即在实证研究中，要提高区分度等值精度，也只需增加每一题本内的样本容量即可。就多级计分而言，区分度等值精度随样本容量的变化更为明显，其趋势与模拟研究结果也更为一致，即当题本数量为3个和7个时，区分度等值精度在样本容量为3 000人时最好，而题本数量为5个时，区分度等值精度在2 000人最好。也就是说，多级计分时，实证研究结果同样表明：当选择较少或较多的题本数目进行施测时，同样需要增加每一题本内的施测人数，才能达到最好的等值效果；而当题本数量适中时，每一题本样本容量适中即可，换句话讲，比较经济的做法是选择5个题本2 000人的搭配。

3.4.3 难度参数的RMSD

难度参数的RMSD如表8所示。

由8表可知，各个条件下的RMSD均在0.43以下，其中0/1计分项目的RMSD范围在0.1817～0.4024；多级计分项目的RMSD范围在0.1716～0.4295。不同条件下难度参数等值的RMSD变化趋势见图4。

从图4可以看出，总体而言，与模拟研究结果类似，无论在何种样本容量及何种题本数量下，0/1计分项目的难度参数等值精度都要好于多级计分项目，但差异并不如模拟研究结果明显。0/1计分时，与模拟研究稍有不同，难度参数等值的RMSD随着样本容量的增加而降低，但2 000人与3 000人时差异并不大，并且无论在何种样本容量下，均为选择3个题本较适宜。多级计分时，难度参数等值精度与模拟研究结果也大体相似，也呈现出随样本容量增加精度更好的趋势，3 000人时，各题本之间几乎无差异。纵观各样本容量下各题本的差异，可发现，3个题本和2 000人的搭配是较为适宜的，如果要进一步提高等值精度，只需将人数增加至3 000人即可。

表8难度参数的RMSD

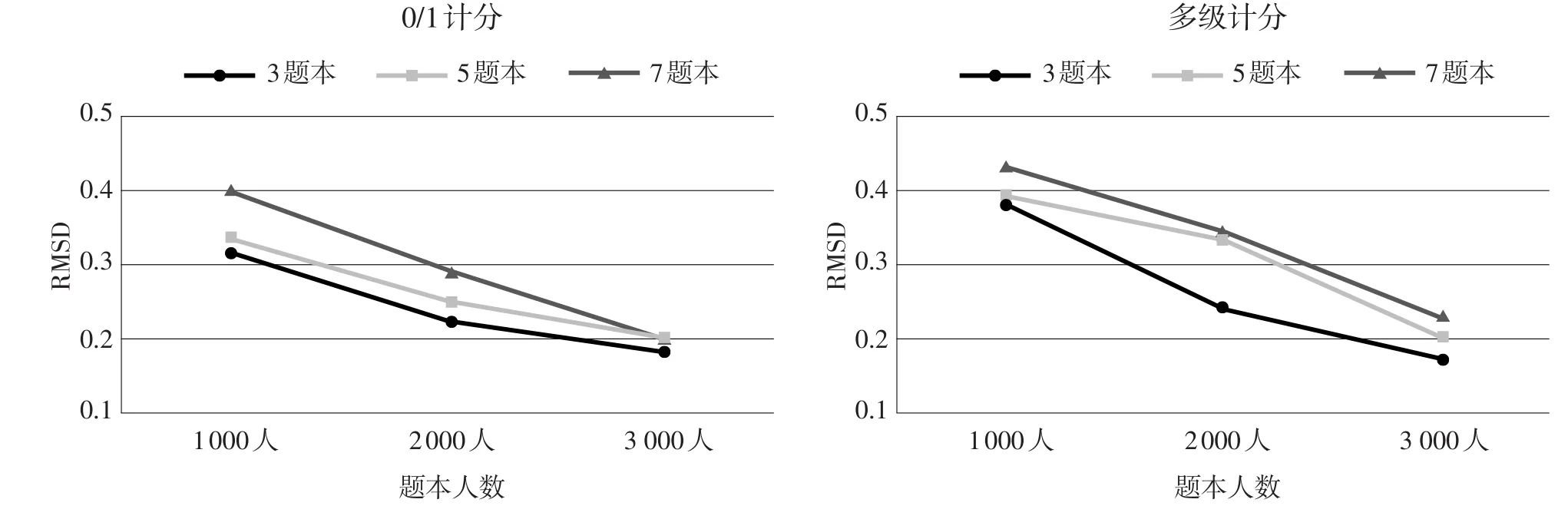
图4不同条件下难度参数等值的RMSD变化趋势

4 讨论与结论

对于项目参数的等值误差来说，0/1计分项目在大多数条件下均小于多级计分项目，这一研究结果与戴海琦等人的研究基本一致[7]。本项研究结果表明，样本容量对于提高项目参数等值精度的作用相较于题本量来说更大，马洪超的研究发现考生样本量影响等值精度，样本量为2 000人左右时的等值结果较稳定，考生样本量进一步增大等值误差减小[12]；本项研究第3个研究结果表明，无论是区分度参数还是难度参数，均表现为3个题本2 000人的搭配已经可以达到较好的等值精度，如果要进一步提高等值精度，只需将每一题本的样本容量增加到3 000人即可；在多级计分情境选用5个题本时，每一题本2 000人是最适宜的组合，这一点以往研究并未涉及。

就项目参数等值误差而言，0/1计分项目在大多数条件下均小于多级计分项目的原因，可能在于多级计分项目比0/1计分项目难以控制，因不同评分者的评分标准不同而造成较多的测量误差，从而在未等值之前就已经引入了较大的测量误差，最终导致等值误差的增大。研究发现，样本容量的增加对于提高项目参数等值精度有着重要的作用，样本容量是影响随机误差的重要因素，增大样本量可以减小测量的随机误差，进而减小等值误差最终提高等值精度；研究表明，增加题本数量对于提高等值精度的作用不大，而杨涛等人的研究表明，提高题本数量会降低等值精度，两者结果不同的原因，可能在于杨涛等人的锚题配置方式为固定锚题，题本量的增加意味着链接次数的增加，每次链接或多或少会引入误差，题本数的增多会最终导致后面链接的题本的项目参数等值误差的增大，而本项研究的锚题配置方式为循环锚题，随着题本数的增加等值精度变化不大。本项研究通过模拟和实证研究探讨了在NEAT设计下，3种施测人数（1 000人、2 000人、3 000人）、3种题本量（5个、7个、9个）、2种锚题题型（0/1计分题、多级计分题）下的项目参数等值效果，得到下列结论：

（1）0/1计分项目参数的等值精度在大多数条件下均好于多级计分项目，实证研究的差异相对不如模拟研究明显。

（2）相对而言，样本容量的增加对于提高项目参数等值精度有着重要的作用，而增加题本数量的作用甚微。

（3）无论是区分度参数还是难度参数，均表现为3个题本2 000人的搭配已经可以达到较好的等值精度，如果要进一步提高等值精度，只需将每一题本的样本容量增加到3 000即可；在多级计分时，当选用5个题本时，每一题本2 000人是最适宜的组合。

[1]李凌艳,辛涛,董奇.矩阵取样技术在大规模教育测评中的运用[J].北京师范大学学报（社会科学版）,2007（6）:19-25.

[2]张忠华,宋萑.共同题数量和测验长度对项目参数等值精确性的影响[C]//第十届全国心理学学术大会论文摘要集.上海，2005.

[3]蔡艳,丁树良,涂冬波.铆题比例对等值精度的影响[J].心理学探新,2009,29（2）:86-89.

[4]熊建华,叶新蓉,丁树良,等.等值设计中锚题比例研究[C]//教育技术与培训国际大会论文集.武汉，2010.

[5]SHINHARAY S,HOLLAND P W.Is It Necessary to Make Anchor Tests Mini-Versions of the Tests Being Equated or Can Some Restrictions Be Relaxed?[J].Journal of Educational Measurement,2007,44（3）:249-275.

[6]LIU J,SHINHARAY S,HOLLAND P W,et al.Observed score equating using a mini-version anchor and an anchor with less spread of difficulty:A comparison study[J].Educational and Psychological Measurement,2011,71（2）:346-361.

[7]戴海崎,刘启辉.锚题题型与等值估计方法对等值的影响[J].心理学报,2002,34（4）:37-40.

[8]黎光明,张敏强.全测验与锚测验题型分值比对等值误差的影响[J].考试研究,2009（3）:73-80.

[9]KOLEN M J,BRENNAN R L.Test equating,linking,and scaling:Methods and practices（2nd ed.）[M].New York,NY:Springer，2004.

[10]杨涛,辛涛,高燕.大尺度教育测评中IRT等值方法的比较研究[J].中国软科学,2013（12）:158-164.

[11]刘玥,刘红云.不同铆测验设计下多维IRT等值方法的比较[J].心理学报,2013（4）:466-480.

[12]马洪超.考生样本量对项目反应理论（IRT）等值稳定性的影响[J].考试研究,2011（2）:62-66.

（责任编辑：周黎明）

A Research on the Influence Factors of IRT Equating in Large Scale Assessments

ZENG Pingfei1,LI Yuqin1,LIU Wenhui2,JIAO Liya3,KANG Chunhua1
（1.College of Teacher Education,Zhejiang Normal University,Jinhua 321004,China;2.Nexchip Semiconductor Corporation,Hefei 230012,China;3.National Education Examinations Authority,Beijing 100084,China）

Simulation study and empirical research are conducted to investigate the influence of sample size,the number of booklets,the item format on IRT parameter equating.Findings show that:a）dichotomous items produce small parameter equating errors than polytomous items,relatively,the difference between empirical research is not as obvious as the simulation study;b）relatively,the increase in sample size plays an important role in improving the equivalent accuracy of the parameters,but the effect of increasing the number of booklets is negligible;c）whether it is the a-parameters or the b-parameters,the matching of three booklets and 2 000 sample size has been able to achieve better accuracy.To further improve the equating accuracy,only the 3 000 sample size is needed.When using polytomous items,five booklets and 2 000 sample size are the best combination.

IRT;Equating;Concurrently Estimation;NEAT Design

G405

A

1005-8427（2017）09-0022-9

10.19360/j.cnki.11-3303/g4.2017.09.003

本文获得教育部人文社会科学研究一般项目（项目编号：16YJA190002）资助。

曾平飞（1963—），男，浙江师范大学教师教育学院，教授；李雨秦（1993—），女，浙江师范大学教师教育学院，在读硕士；刘文惠（1992—），女，合肥晶合集成电路有限公司，管理师；焦丽亚（1982—），女，教育部考试中心，助理研究员；康春花（1974—），女，浙江师范大学教师教育学院，副教授。