基于Rasch模型的参数估计方法比较研究

王佶旻 李潇

（1.北京语言大学，北京 100083；2.北京师范大学，北京 100875）

基于Rasch模型的参数估计方法比较研究

王佶旻1李潇2

（1.北京语言大学，北京 100083；2.北京师范大学，北京 100875）

本研究的目的是基于Rasch模型，比较联合极大似然估计法、边际极大似然估计法和EM算法、边际贝叶斯估计法参数估计结果的准确程度。实验数据为2 185名被试在HSK试卷170道试题中的作答矩阵，考虑到初值和收敛精度对参数估计结果的影响，将三种参数估计方法按照初值设置和收敛精度不同分别进行参数估计，然后通过计算项目参数估计标准误判断参数估计方法的准确度。

项目反应理论；参数估计；联合极大似然估计法；边际极大似然估计法和EM算法；边际贝叶斯估计法

1 引言

1952年，美国测量学家Frederic M.Lord在自己的博士论文中将能力与答对率之间的函数关系用双参数正态拱形曲线模型（Two-parameter Normal Ogive Model）描述出来，并基于这一模型建立了一套项目反应理论（Item Response Theory，简称为IRT），同时提出了相应的参数估计方法[1]。

至今，项目反应理论模型在不断发展演变，参数估计方法也是层出不穷。目前应用最广泛的参数估计方法有联合极大似然估计法、边际极大似然估计法和EM算法以及边际贝叶斯估计法。从算法的角度分析，Mislevy R.J和Stocking M.L认为贝叶斯估计法更为精确；Baker和Kim也认为由于边际贝叶斯估计法利用了更多参数的先验信息，因此估计结果会更加稳定和精确[2]。

目前运用实证数据对这三种参数估计方法进行比较的研究并不多，基本都采用现成的商业软件来估计模拟作答矩阵的各项参数，再进行方法的比较。缺点显而易见，首先，蒙特卡洛模拟数据概率分布过于规则化，无法代表真实的作答反应；其次，进行参数估计的各种商业软件的功能以及默认的参数设置并不统一，这将给实验结果带来不可避免的系统误差。

有鉴于此，本文采用汉语水平考试（HSK）［初、中等］真实考生数据作为实验材料，运用VFP6.0[3]自行编制的程序进行参数估计。这样可以将三种方法的初值、迭代次数和精度，先验信息的分布参数都控制好，以保证参数估计方法的可比性。为了降低编程难度，本研究选择最简单的Rasch模型进行参数估计。Rasch模型如下：

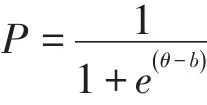
P表示能力为θ的被试答对难度为b的题目的概率[4]。

2 参数估计方法

2.1 联合极大似然估计法

Birnbaum在1968年提出联合极大似然估计法的概念。

假设被试作答模式相互独立，同一被试对各个项目的作答相互独立，Uaj表示a个被试在第j个项目上的反应。似然函数如公式①所示，对数似然函数如公式②所示。

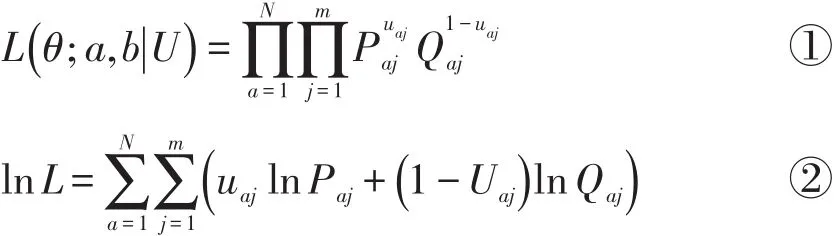
其中Paj为被试a在第j个项目上的答对概率；Qaj=1-Paj。

接下来对θ参数（或b参数）设置初始值，求取使似然函数最大化的b参数，再代入b参数，求取新的θ参数，循环往复，直到似然函数最大值收敛。

联合极大似然估计法帮助项目反应理论完成了从理论向实践的飞跃，但是，仍然暴露了很多问题。首先，如果一个被试答对或者答错了全部题目，那么被试的能力就无法被估计；其次，当被试的能力所对应的项目难度出现断层时，似然函数在极值点附近就会显得比较平坦，从而造成迭代无法收敛于定值，当然对于题目的难度估计也是如此；再次，难以确定合理的初值；最后，能力参数的个数依赖于样本量的变化，但是项目参数永远固定，随着样本量的增加无法保证项目参数估计的恒定性[5]。

2.2 边际极大似然估计法和EM算法

边际极大似然估计与联合极大似然估计最大的不同点在于，前者假设已知被试的能力先验分布，将被试看成从这一能力总体中抽取的样本，然后根据贝叶斯定理，将似然函数中的能力参数通过积分去掉，得到仅含有项目参数的边际似然函数，然后再用边际似然函数导出项目参数的边际似然估计。

由于边际似然估计法的计算量过大，需要通过EM算法来真正得以实现。EM算法实际上也是极大似然估计法中求参数的一种迭代方法。它分为两个步骤，分别是期望步骤E步和最大化步骤M步。我们将EM算法应用在项目反应理论中，那么就是未观察数据，反应矩阵U为可观察数据。为的联合概率密度函数，其中ζ为项目参数。我们先给项目参数ζ设定一个初值，代入这个值计算出似然函数条件分布的期望值，这样就使得大量含有未知参数的表达式变成了期望常数。通过最大化步骤M步得到第一次估出的项目参数后，把参数再代入期望步骤E步，调整期望值，继续修正项目参数，直到参数收敛为止。采用这种算法，大大简化了边际极大似然估计的计算，同时消除了能力参数的影响。

边际极大似然估计法和EM算法仍然存在很多不足。首先，这种方法仍然无法估计特殊的反应模式；其次，在迭代求项目参数时，有些特定数据会使得区分度被估计得过大，而接近于零的区分度又会导致难度的绝对值增大；再次，EM算法的迭代速度很慢，而且是想要的结果越精确，迭代的速率就越慢。

2.3 边际贝叶斯估计

如前所述，在边际极大似然估计法中，得满分或得零分的被试都无法估计其能力，而所有被试都答对或答错的题目也无法估计其难度。边际贝叶斯估计法则解决了这个难题。

贝叶斯参数估计法其实是对边际极大似然估计法的延伸，因此也被称为边际贝叶斯参数估计法。它与后者的最显著区别是后者不仅要给出被试的能力先验分布，同时还要给出所有待估参数的先验分布。

由贝叶斯定理可知：

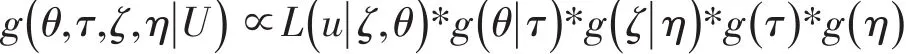
其中g(θ|τ)为能力参数的先验分布；为项目参数的先验分布；为基于U的似然函数。

边际贝叶斯估计法的参数估计步骤与边际极大似然估计法基本是一样的，只是在似然函数中加入了项目参数和能力参数的先验信息，将参数值自动限制在可接受的范围内。因此，即使测试中出现一个被试在所有项目全部正确作答或错误作答的情况，也不会被无限估计。

3 实验

3.1 算法评价标准

我们设计了三个参数估计实验，每个实验使用一种参数估计方法得到能力参数和难度参数，再通过计算项目参数估计标准误作为评价参数估计精确度的指标。标准误越小，表示估计越精确。项目参数估计标准误[6]是由Lord提出的，是从测验信息函数演变而来的衡量参数估计精确度的指标[7-8]。

bi的项目参数估计标准误表示为：

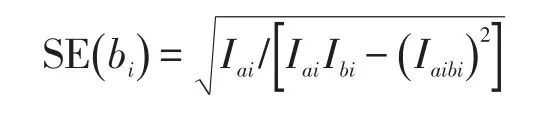
其中，

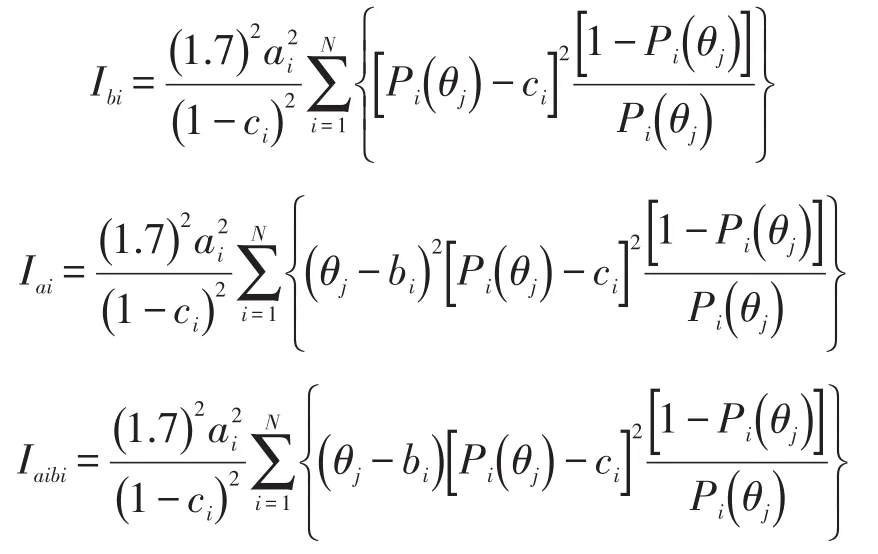
在Rasch模型中，a=1，c=0。

需要说明的是，求标准误的前提条件是我们假定能力参数为真值且已知。因此，在实际应用的过程中，由于能力参数也是被估计出来的，会导致项目参数的标准误被低估。但是只要样本量足够大（＞2 000人），被低估的现象就可以被忽略[7]。

3.2 筛选被试

由于参加HSK［初、中等］考试的31 648名考生原始总分呈明显的负偏态分布（如图1所示），为了满足极大似然估计法的要求，尽量保证每道题目的难度和每个被试的能力能够相互匹配，我们在实验之前对全部考生数据进行了分层抽样和极端值剔除。

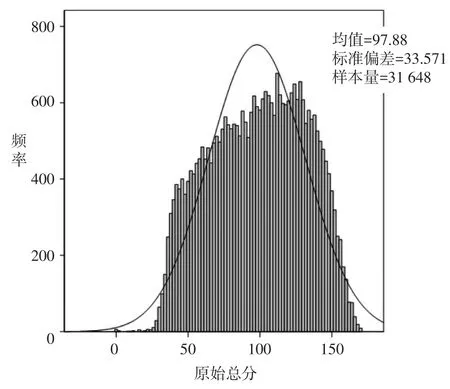
图1全体被试的原始总分分布

第一步：分层抽取被试样本

在剔除极端值被试样本（分数为0分和170分）之后，根据正态分布表每段分数所占全部分数的百分比进行抽样，得到基本符合正态分布的2 301人被试样本，如图2所示。

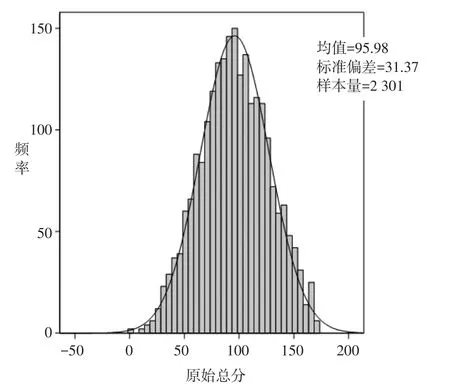
图2抽样被试原始总分分布

第二步：为避免能力异常值出现，剔除答对率在猜测概率（25%）以下的被试（共116人），得到最终参加实验的被试人数为2 185人。

3.3 初值和收敛精度

本实验分别对相同样本采取两种初值计算方法：第一种方法是Lord提出的初值设定方法，我们简称Z分数法。能力初值为被试原始分数的标准分数Zj，难度初值为Zi/rbi（Zi为每道题答对率的标准分数，rbi为每道题的双列相关值）；第二种方法首先根据漆书清和戴海琦提出的能力初值计算方法得到能力初值[7]，我们简称对数法：

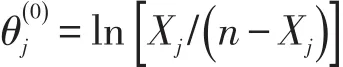
其中，Xj为被试j在测试中答对题数的个数，n为题目总数。

接下来，设定难度初值为：

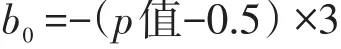
经过参数预估后发现，难度初值设为Zi/rbi时，三个实验均出现了参数无法收敛的现象。我们只好对Z分数法中的难度初值作出调整，也采用对数法进行计算。因此，本实验中“Z分数法”和“对数法”的初值计算差异仅体现在能力上。

本实验设置两个收敛精度分别是0.01和0.001。

3.4 实验一

3.4.1 实验设计

实验一对Rasch模型进行联合极大似然估计，根据初值和收敛精度的不同，设计了四个子实验，如表1所示。

表1子实验分类

表2各子实验的迭代次数和项目参数估计标准误

3.4.2 结果分析

我们对四个子实验基本收敛（收敛率在95%以上）所需要的迭代次数以及在达到最大收敛率时各个子实验的全卷项目参数估计标准误进行了统计，具体数值如表2所示。

由表2可以看出，以Z分数法作为初值的联合A、B子实验收敛效率均较高，都是10次迭代后收敛率就达到了95%以上。其次是联合D子实验，迭代次数为11次。收敛效率最低的是利用对数法计算初值且收敛精度为0.001进行参数估计的联合C子实验。而四个实验的项目参数估计标准误最低的是联合A子实验，数值为12.518，最高的是联合C子实验，数值为13.322。

接下来，我们就初值、收敛精度对收敛率和项目参数估计标准误的影响做进一步的分析。

（1）初值和收敛精度对收敛率的影响

从图3我们可以看出，四个子实验由于初值不同，收敛精度不同，收敛率与迭代次数相对应的变化趋势还是有一些差别的：联合D子实验由于精度设置较低，收敛效率明显高于联合C子实验。相对而言，联合A、B子实验并没有在收敛效率上呈现太大的差异（不明原因导致联合A子实验在第12次迭代时收敛率极低，我们认为属于偶然现象），它们的收敛趋势也是比较相近的。

就收敛的效果而言，联合D子实验和联合A子实验都是比较理想的。不仅从第五次迭代开始就有较高的收敛率，收敛率的最大值也分别达到了100%和99.41%的高水平。

从实验结果来看：收敛精度对联合极大似然估计法的收敛效率产生影响，收敛精度越高，收敛效率越低，反之亦然。而初值则对参数估计收敛率的变化趋势和收敛效率均有较大影响（对参数是否收敛也起到重大作用，如难度初值设为Zi/rbi时，迭代根本无法收敛）。总体来说，利用Z分数法设定能力初值相比于利用对数法计算能力初值收敛效率更高，迭代效果更好一些。

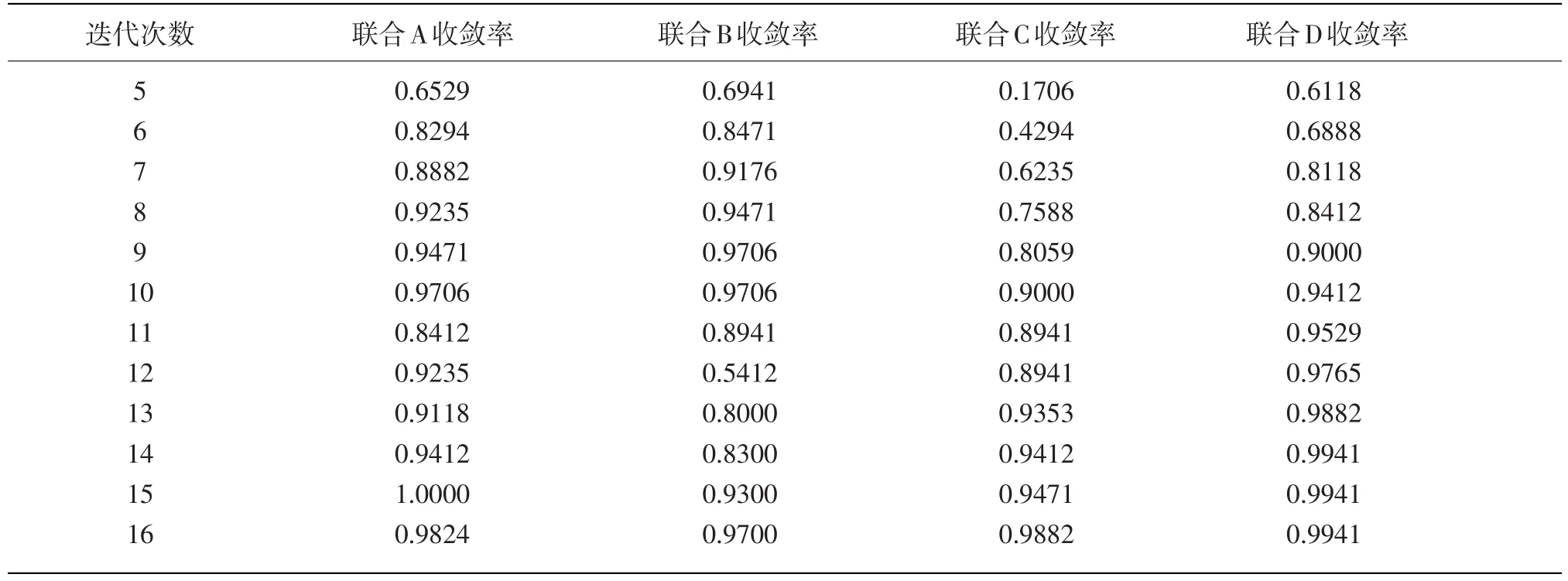
表3各实验在不同迭代次数下的收敛比率

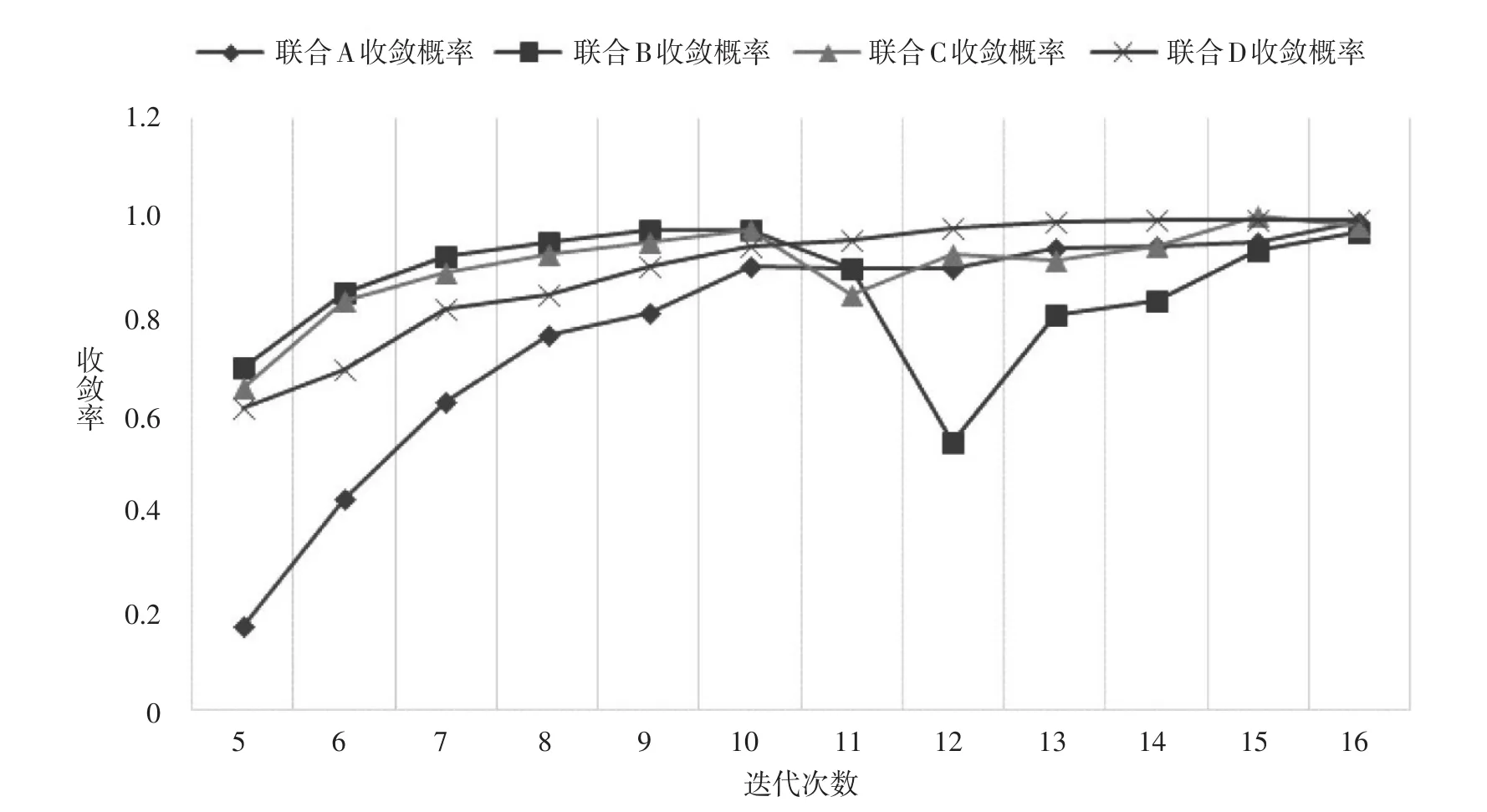
图3各子实验的收敛概率变化趋势

（2）项目参数估计标准误

我们将四个子实验的参数估计结果利用自编的VFP程序进行了项目参数估计标准误的计算。根据收敛率和迭代次数的关系，我们分别取迭代次数为10、迭代次数为15，以及四个实验各自收敛率达到最大的迭代次数所对应的参数估计结果计算了项目参数估计标准误。

由表4可以看出，在迭代10次之后，项目参数估计标准误最低的是联合B子实验，数值为12.722。标准误最高的是联合C子实验，数值为14.099。联合A、D子实验的标准误基本相同，分别是13.018和12.976。结合标准差来看，联合C子实验的标准差最高，为0.065，联合D子实验的标准差最低，为0.047。由此来看，联合C子实验所估计的参数值无论是从准确性还是稳定性来看都是四个子实验中最差的。而联合B子实验参数估计的准确性最高，但稳定性稍差。其次是联合D子实验的结果，虽然准确性不如联合B子实验，但是标准差最低，说明参数估计准确度的稳定性相对高一些。

如表5所示，我们更换成迭代15次的数据后，各个实验的项目参数估计标准误与参数估计标准差出现了变化。总体来说，在换成迭代15次的数据之后，联合A子实验无论是在参数估计的准确度还是稳定性来看都是最好的，相比而言联合B、C子实验的结果则不太理想。

表4迭代10次后计算项目参数估计标准误的统计量数据

表5迭代15次后计算项目参数估计标准误的统计量数据

表6取最大收敛率的迭代次数计算项目参数估计标准误的统计量数据

最后，我们分别选择各个子实验中收敛率最大的迭代次数中的参数值计算项目参数估计标准误。得到的数据如表6所示。我们发现，与“迭代10次”和“迭代15次”的数据相比，四个子实验的项目参数估计标准误以及标准误的标准差均有所下降。相比而言，联合C子实验的标准误是全部实验中最高的，达到了13.322。

我们将各个实验的项目参数估计标准误以及收敛率的变化趋势绘成图表如图4和图5所示。

我们从图4中可以看出，利用对数法计算初值，且精度设为0.001（高精度）的联合C子实验基本都处于高标准误的水平；利用Z分数法计算初值，且精度设为0.001（高精度）的联合A子实验以及利用对数法计算初值且精度设为0.01（低精度）的联合D子实验的项目参数标准误走势很相似且都处于数值较低的水平；而利用Z分数法计算初值，且精度设为0.01（低精度）的联合B子实验在收敛率的影响下标准误的数值波动较大。

我们比较图4和图5不难发现，收敛率和项目参数估计标准误的变化趋势基本呈水平对称。也就是说，收敛率会直接影响项目参数估计标准误，且收敛率越高，项目参数估计标准误越低。

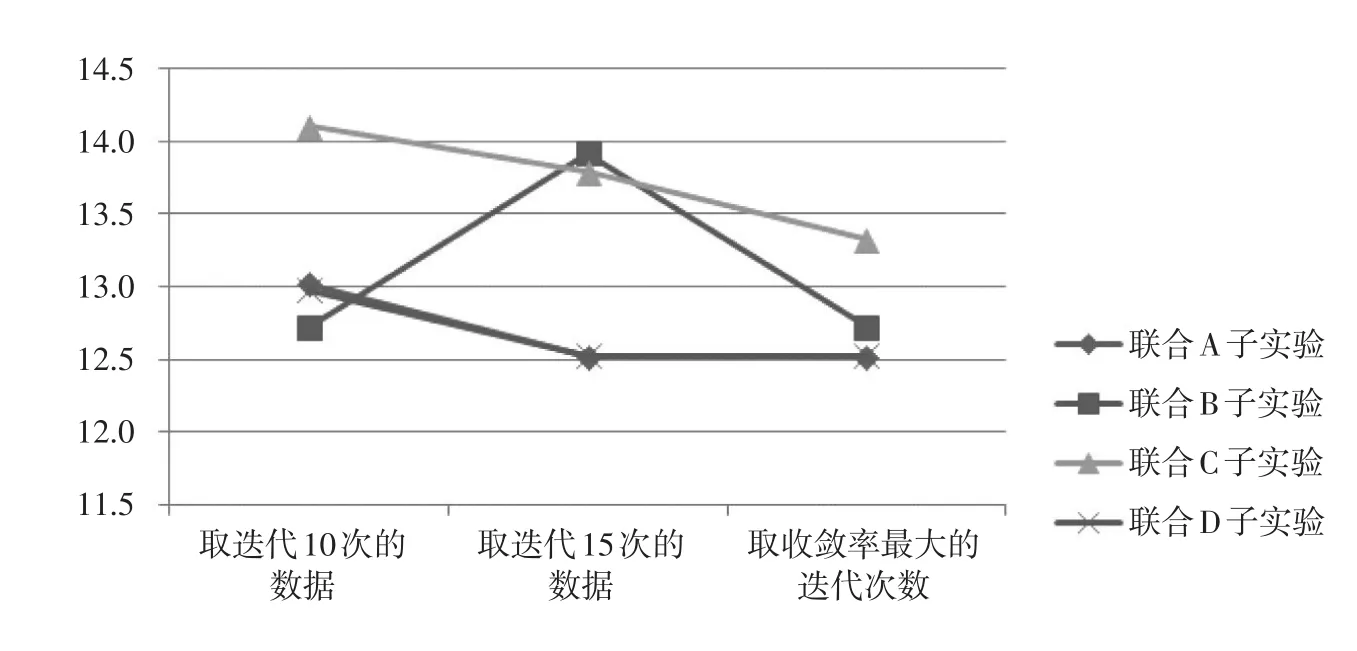
图4各个子实验的项目参数估计标准误变化趋势

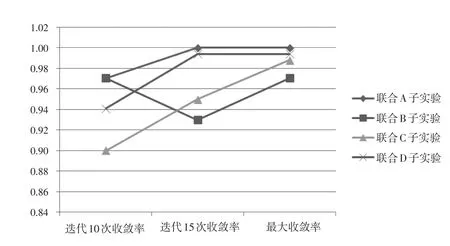
图5各个子实验的收敛率变化趋势

3.5 实验二

3.5.1 实验设计

本实验对Rasch模型利用边际极大似然估计法和EM算法进行参数估计。与实验一不同的是，边际极大似然估计法和EM算法只需要求取难度参数初值。由于“Z分数法”和“对数法”求难度初值的过程是相同的。因此本实验只根据收敛精度的差异设计了2个子实验，如表7所示。

表7子实验分类

实验过程中，我们运用BILOG软件估计全体被试能力值，以及全体被试能力的求积节点和权重。

从理论上讲，被试能力的先验分布是先前无数次测验信息积累得到的结果。但是由于客观条件限制，我们无法得到测验分布累积的数据。因此决定采用全部被试（31 648人）的能力分布代替这2 185人的能力先验分布。利用SPSS计算得出被试总体的能力参数分布直方图，如图6所示。

图6全体被试能力值分布

根据SPSS的统计结果来看，被试能力值基本呈现均值为0、标准差为1的标准正态分布。

我们根据被试总体的能力分布利用BILOGMG软件计算出10个能力求积节点和相应的权重，如表8所示。

3.5.2 结果分析

与联合极大似然估计法相比，边际极大似然估计法和EM算法最大的优点就是收敛效率非常高。联合极大似然估计法一共迭代了16次，而边际极大似然估计法和EM算法都是估计两次就可以成功收敛。并且每次估计的运算速度也相比前者要快很多。

但需要说明的是，边际极大似然估计法和EM算法在估计出难度参数之后，只能估计出能力参数的后验分布概率，而无法得到确切的能力参数值。因此，在实践中，这种方法只用来估计项目参数，能力参数的估计还要依靠联合极大似然估计法或边际贝叶斯估计法来实现。

我们对两个子实验的项目参数估计标准误进行了描述性统计分析，结果如表9所示（统一采用对数法迭代15次的能力参数值计算项目参数估计标准误）。

我们可以看出，边际A子实验和边际B子实验受收敛精度的影响并不大，数值基本相同，标准差也基本趋于一致。

3.6 实验三

3.6.1 实验设置

实验三采用边际贝叶斯估计法进行参数估计。边际贝叶斯估计法是边际极大似然估计法和EM算法以及联合极大似然估计法相结合的产物。在估计项目参数时算法与前者基本一致，在估计能力参数时，算法与后者基本一致。本实验根据收敛精度和初值设置差异分为四个子实验（与实验一相同），如表10所示。

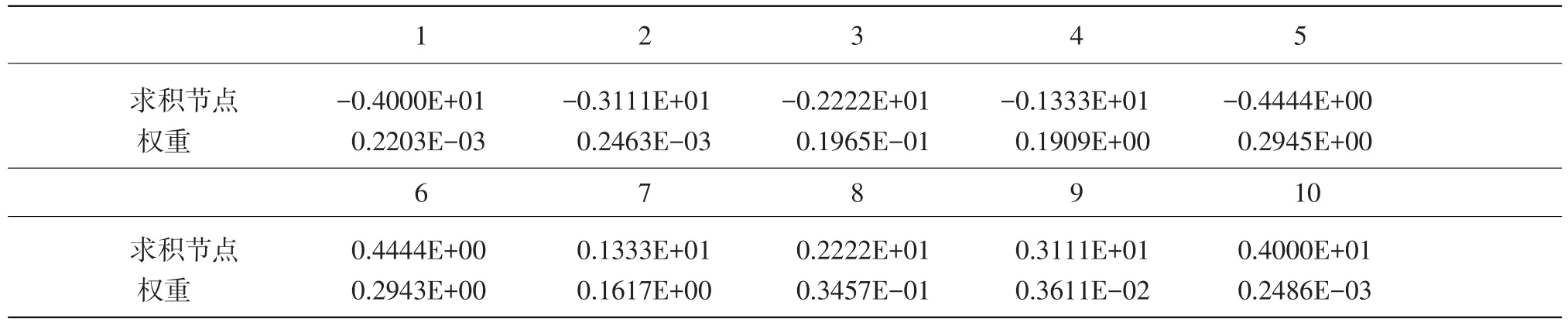
表8 10个能力求积点和相应的权重

表9项目参数估计标准误的统计量数据

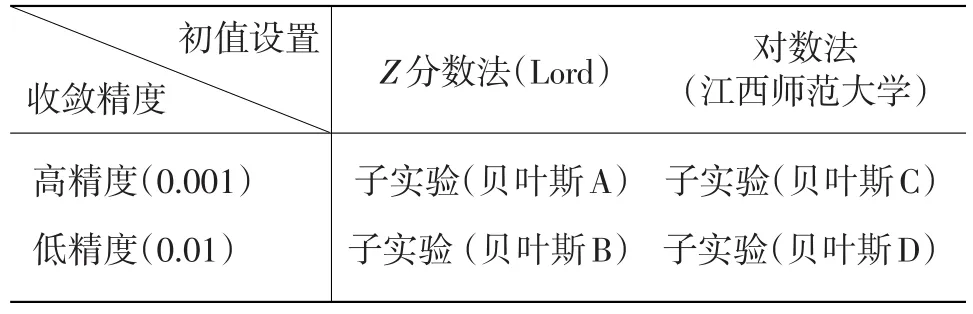
表10子实验分类

在边际贝叶斯估计法中不仅需要得到被试能力参数的先验分布，还要求得到项目难度参数的先验分布。我们根据全体被试样本（共31 648人）的作答矩阵，利用BILOG-MG软件，对170道题的难度参数进行估计，并利用SPSS软件得到难度参数的分布如图7所示。

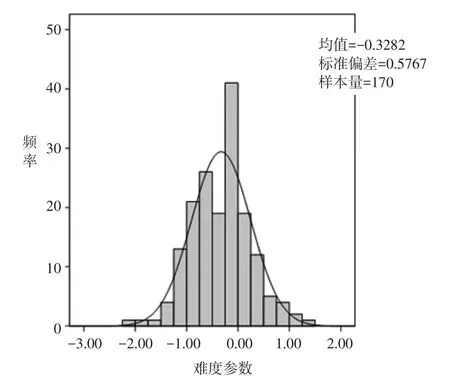
图7难度参数先验分布

SPSS软件的统计数据显示：难度参数基本服从平均值为-0.3282、标准差为0.5767的正态分布。我们以此作为难度参数的先验分布。

3.6.2 结果分析

由于边际贝叶斯估计法在求取能力参数时不需要反复迭代，因此在统计收敛精度和迭代次数的关系时无须考虑能力初值的影响。经过计算我们发现，边际贝叶斯估计法无论在高精度还是低精度的情况下，两次收敛率均达到100%，项目参数估计标准误则随着初值和收敛精度设置不同略有差异。表11为四组子实验的项目参数估计标准误的描述统计量。

从表11可以看出，四组子实验的项目参数估计标准误差异是很细微的。在高精度水平上，贝叶斯C子实验比A子实验的标准误略低；在低精度水平上，贝叶斯D子实验比B子实验的标准误略低。这说明在同一收敛精度下，利用对数法计算初值比利用Z分数法代替能力初值所得参数结果要准确一些；在以Z分数求取初值的贝叶斯A、B子实验中，收敛精度高的A实验的标准误低于收敛精度低的B实验；在以对数法求取初值的贝叶斯C、D子实验中，收敛精度高的C实验的标准误高于收敛精度低的D实验。这说明以Z分数法计算初值时,高收敛精度估计结果更准确，而以对数法计算初值时，低收敛精度估计结果反而更理想。这一点与联合极大似然估计法的实验结果是一致的。

表11项目参数估计标准误的统计量数据

3.7 三组实验数据汇总

我们将联合极大似然估计法实验（取最大收敛率所对应的迭代次数计算标准误）、边际极大似然估计法和EM算法实验、边际贝叶斯估计法实验共10个子实验的项目参数估计标准误进行横向对比，数据如表12所示。

由表12和图8可以看出，三种实验方法中联合极大似然估计法参数估计的准确性最低；边际贝叶斯估计法的标准误均值为5.658，参数估计的准确性最高。

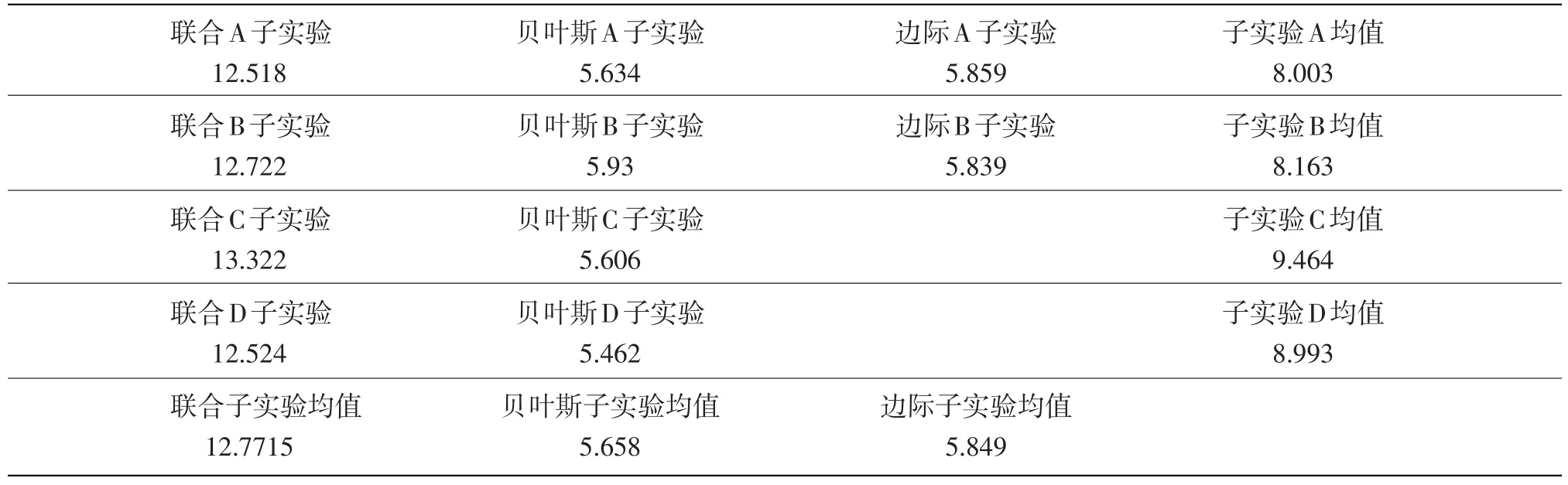
表12各实验项目参数估计标准误对比

图8各实验项目参数估计标准误变化趋势

初值和收敛精度不同对于联合极大似然估计法影响最大，而对于边际贝叶斯估计法以及边际极大似然估计法和EM算法的影响是非常微弱的。

从A、B、C、D四组子实验项目参数估计标准误的均值来看，收敛精度对标准误的影响随着初值设置的改变而有所不同。

4 结论

从参数估计方法的准确性和稳定性来看，联合极大似然估计法的参数估计结果不仅精度低，而且容易受到初值和收敛精度的影响，稳定性也比较差。导致这一结果的原因可能是：（1）似然函数在构建的过程中没有充分利用被试总体和项目总体的先验信息分布，导致在估计能力过高或过低的被试（难度过难或过易的项目）时容易出现异常值；（2）在迭代求取非线性方程的未知参数时，由于多个驻点的存在，我们无法保证选取的初值就在最大值所在定义域范围内，因此导致收敛于伪值或不收敛的概率大大增加；（3）联合极大似然估计法要求每个能力值和难度值的被试与项目匹配，当某个能力的被试找不到适合他难度的试题时，参数估计精度就会降低。

相比于联合极大似然估计法，边际极大似然估计法和EM算法以及边际贝叶斯估计法则在准确度方面体现出比较大的优势。主要原因是这两种方法都在计算的过程中充分利用到了被试总体的能力先验分布，尤其是边际贝叶斯估计法，在构造似然函数时又加入了项目参数先验分布的表达式。先验分布可以把异常值收缩到参数均值附近，从而提高参数估计的准确性和稳定性。

从初值设置对参数估计结果的影响来看，利用原始分数的Z分数值代替能力初值更适用于联合极大似然估计法。原因可能是Z分数值与被试能力参数的正常范围比较吻合；而通过对数法计算的初值基本与正常能力值相差较远，对最终的参数估计结果产生不利影响；而在边际贝叶斯估计法中，先验分布函数起到了收缩能力初值的作用，因此最终的参数估计结果并不会受到很大影响。

收敛精度和初值设置会对参数估计结果产生交互影响。遗憾的是，我们还不清楚产生交互影响的真正原因。这是一个值得进一步深入分析和研究的问题。

[1]LORD F M.A theory of test scores[J].Psychometric Monograph,1952（7）.

[2]FRANK B BAKER,SEOCK-HO KIM.Item Response Theory Parameter Estimation Techniques[M].New York:Marcel Dekker,Inc,2004.

[3]鲁俊生.VFP程序设计简明教程[M].西安:西安电子科技大学出版社,2010.

[4]漆书清,戴海琦,丁树良.现代教育与心理测量学原理[M].北京:高等教育出版社,2003．

[5]NEYMAN J,SCOTT E L.Consistent estimates based on partially consistent observations[J].Econometrica,1948（16）:1-32.

[6]LORD F M.Applications of item response theory to practical testing problems[M].Hillsdale,NJ:Erlbaum,1980.

[7]漆书清,戴海琦.项目反应理论及其应用研究[M].南昌:江西高校出版社,1992.

[8]HAMBLETON R K,SWAMINATHAN H,ROGERS H J.Fundamentals of item response theory[M].Newbury Park,CA:Sage Publications,1991.

（责任编辑：周黎明）

The Comparison between the Method of MLE,MLE/EM and BMES under the Rasch Model

WANG Jimin1,LI Xiao2
（1.Beijing Language and Culture University,Beijing 100083,China；2.Beijing Normal University,Beijing 100875,China）

The objective of this article is to assess the accuracy of the Joint Maximum Likelihood Estimation（JMLE）,the Marginal Maximum Likelihood Estimation/EM algorithm（MMLE/EM）,Marginalized Bayesian Parameter Estimation（BMEs）based on the single parameter logistic model.Experimental subject is the answer matrix of 2 185 examinees,who were tested in the HSK examination（including 170 questions）on Dec 9th,2005.We assessed the accuracy of parameter estimation by comparing the standard errors from each estimation method.This study also conducted the parameter estimation under different initial values and convergence precisions for each approach,taking into account the effects of initial value and convergence precision setting for parameter estimation results.

IRT;Parameter Estimation;JMLE;MMLE/EM;BMEs

G405

A

1005-8427（2017）09-0011-11

10.19360/j.cnki.11-3303/g4.2017.09.002

本研究得到北京市社科规划项目“首都留学生跨文化适应研究”（项目号：13WYB014）和北京语言大学院级项目（项目号：17YJ050011）的资助。

王佶旻（1974—），女，北京语言大学汉语考试与教育测量研究所，教授，博士生导师；李 潇（1987—），女，北京师范大学中国基础教育质量监测协同创新中心，讲师。