表面等离子波仿真研究

李明德，逯贵祯，蓝炳麟

(中国传媒大学 信息工程学院，北京 100024)

表面等离子波仿真研究

李明德，逯贵祯，蓝炳麟

(中国传媒大学 信息工程学院，北京 100024)

先介绍表面等离子波的基本概念、理论发展和模型构建，然后在Kretschmann模型配置下，即介质—金属—介质情况，激励表面等离子波。利用解析方法和数值仿真得到表面等离子波谐振情况，并对金属厚度、介电常数、入射介质、分析物等参数进行灵敏度分析，得到一些基本规律。

表面等离子波；Kretschmann；灵敏度

1 引言

表面等离子波(surface plasmon wave，SPW)的研究历史长达100多年，早期由于受电子元件的工艺水平的限制，不为人们所关注。随着工艺技术的迅猛发展，表面等离子光子学的研究得到极大的促进。1902年，Wood在光学实验中首次发现了表面等离子波现象[1]。1941年，Fano等人根据金属和空气界面上表面电磁波的激发解释了这一现象[2]。1957年，Ritehie发现，当电子穿过金属薄片时，存在数量消失峰，他将这种消失峰称之为“能量降低的”等离子体模式，第一次提出“金属等离子体”的概念[3]。1968年，Otto[4]利用衰减全反射的方法利用三棱镜作为光的耦合器激发表面等离子波。1971年，Kretschmann[7]在Otto的基础上进行了改进，这两种方法至今仍是研究SPW广泛使用的方法。文献[6]在Kretschmann配置下，定性分析了不同参数对谐振角的影响。最近几年随着金属电磁学的新概念、新应用[3][9]的提出，表面等离子光子学研究成为越来越热门的课题。

表面等离子体光子学(surface plasmonics，SP)是一门新兴学科，它的另一名称是表面等离子体激元(surface plasmon polariton，SPP)，指沿金属介质界面传播的纵向电磁波，其电磁场从界面向两边按指数率下降，即消失态[8]。表面等离子波是指外来入射电磁波诱导使金属表面的自由电子在金属与介质的交界面上发生集体振荡，并沿着分界面传播从而形成表面等离子波。表面等离子波是基于波动学的说法，表面等离激元则是基于粒子学的说法，实际就是量化后的称呼，和光波量子化后叫光子是一个道理。正体现了波粒二象性，本质上一样的，都是电磁波和自由电子的相互作用，并且理论分析[9]表明，SPW只能以TM模式传输。

2 理论和模型

表面等离子激元是金属表面自由电子集体振荡的现象，当条件合适时即光子的频率匹配金属表面电子振动的固有频率与正电原子核的恢复力时，沿界面传输的电磁波和自由电子谐振。事实上，激发等离子体共振只能发生有损金属电介质的界面，即当金属介电常数的虚部是负数时。理论分析证明[10]，等离子体共振存在于介电常数符号相反的媒质界面处，且只能是TM波。根据Drude模型[11]，金属在光频下，介电常数一般是负数，并且实部绝对值大于虚部[10]，其虚部代表金属吸收光的能力，一般光在金属中的损耗非常大。电场在界面处达到最大值，向两边媒质呈指数衰减，一般渗透到介质中100nm，而在金属中10nm[9]。如果要使表面等离子波传播距离变长，则要求金属的介电常数具有一个大的负实部占和小的虚部，即低损耗的金属材料。表面等离子波是慢波，跟在常规介质的波相比，具有较大的相速度更短的波长，更高的动量，更高的波阻抗[9]，这是其能够实现纳米集成光路的内在基本原理。在表面等离子波结构中，限制性与损耗是一对永恒的矛盾。如何在限制性与损耗之间找到一个最佳的平衡点，是表面等离子波结构需要重点研究的问题。

一般存在两种等离子体激发的常用配置方法，一种是E.Kretschmann方法，金属薄膜夹在介质和空气之间；另一种是A.Otto方法，空气介于介质和金属薄膜之间。为了方便实际应用本文将采用E.Kretschmann配置，利用数值仿真软件进行分析。

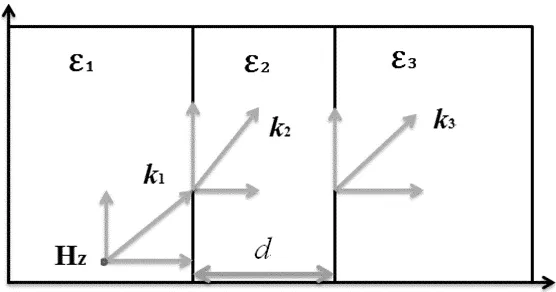
图1 E.Kretschmann模型示意图

模型如图1所示，厚度为d、介电常数为ε2的金属薄膜介于介电常数分别为ε1和ε3的电介质材料之间。表面等离子波只能以TM模式传输，所以将入射波设置成波矢量为k1的TM波，接下来两层，透射波波矢量分别为k2、k3。理论分析参考文献[12]。金属在光频下介电常数是入射波角频率的函数，可由Drude模型[11]表示，本文所采用金属介电常数来源于文献[13] 。仿真时，入射波长取800nm，入射功率取0.1W，此时金属介电常数ε2=-31-j*0.4，ε1=2.25，ε3=1。反射系数随入射角变化曲线如图2，以及反射系数最小时，即谐振情况下，磁场平面分布图3。

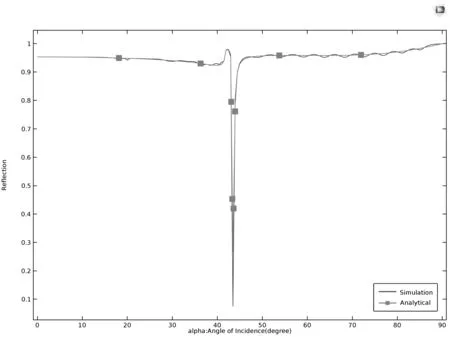
图2 反射系数随入射角变化曲线图

图3 磁场平面分布图

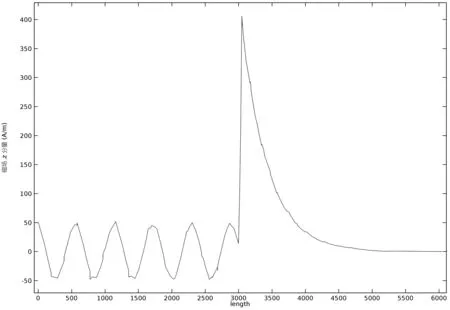
图4 平行x轴中线上磁场分布曲线图

图1中当角度为42.665°时，反射系数达到最小，即达到谐振。曲线极其尖锐，并且其位置对与金属相邻的介质的介电常数异常敏感。 这种灵敏性正是化学检测，生物探测的潜力体现。图2显示，波动沿平面传播，在分界面达到最大值，然后逐渐衰减。图4展示了平行x轴的中线上磁场分布密度，分界面处磁场达到最大值，后逐渐衰减。

3 各个参数对谐振角影响的分析

在E.Kretschmann配置中存在许多参数对谐振角存在重要影响，接下来将通过仿真逐个分析每个参数的影响。

3.1 金属厚度影响

在E.Kretschmann配置中，金属至关重要，包括材料即金属介电常数和金属厚度，先分析金属厚度便于进一步分析其他参数，文献[6]理论分析了金属厚度与金属介电常数及入射光之间的关系并得出公式，具有一定指导意义。仿真分析得到反射系数和金属厚度之间的关系如图5。

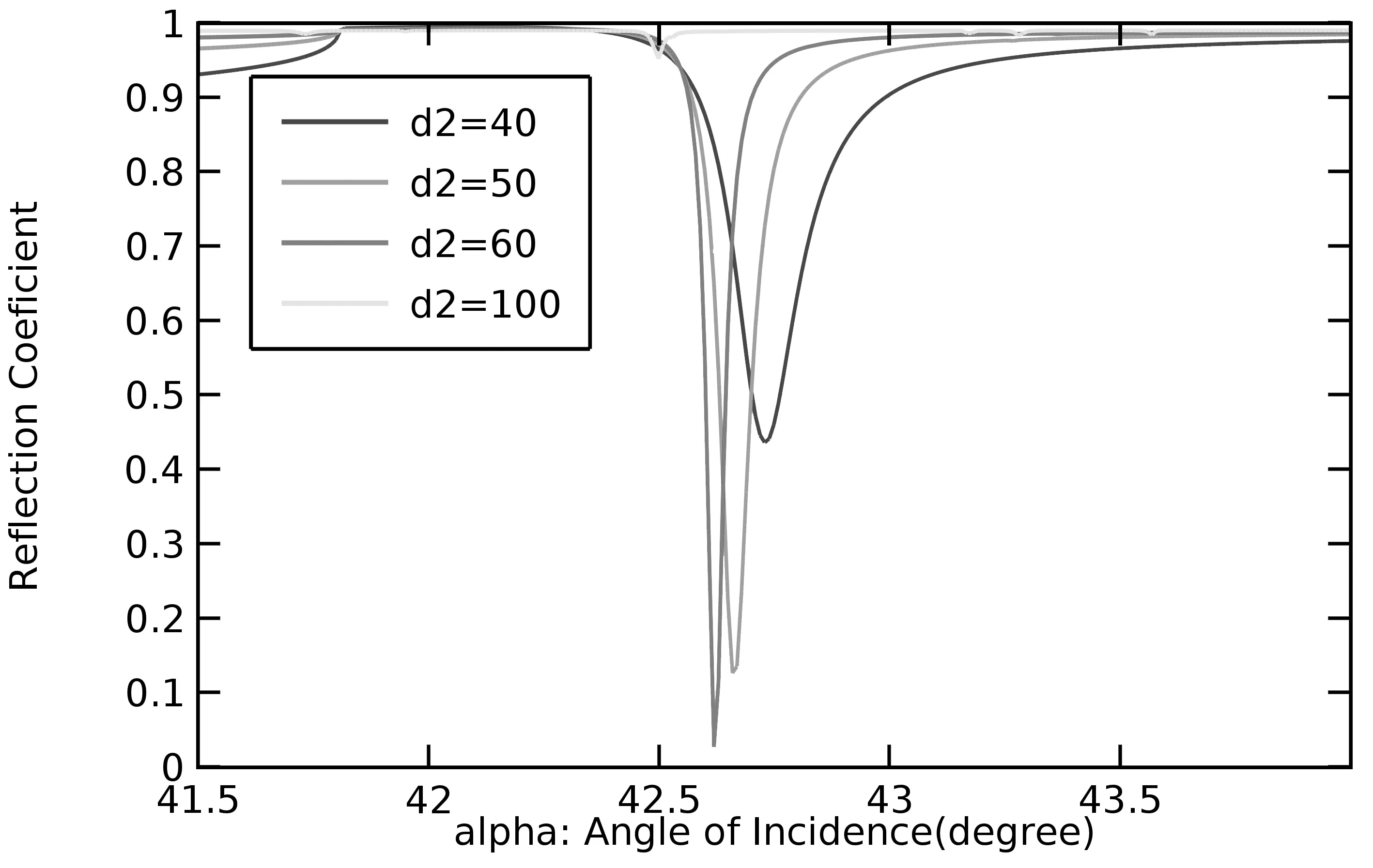
图5 金属厚度(d2)不同时反射系数随入射角变化曲线

当金属厚度不同时，仿真分析表明，金属厚度过大，不产生谐振情况，即光波无法穿透金属，被完全吸收，从而在分析物一侧不产生表面等离子波。在产生谐振前提下，金属厚度越小，反射系数越大，仿真表明40-70nm是比较理想的金属厚度，既能产生表面等离子波，又能保证反射系数较小。

3.2 分析物(ε3)的影响

SPR在生物检测技术中发挥着重要作用，不同检测物体对应着不同谐振角，伴随不同检测物，谐振角灵敏性极高。仿真分析不同分析物反射系数曲线如图6。

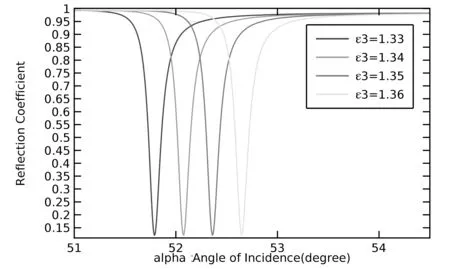
图6 分析物(ε3)不同时反射系数随入射角变化曲线图

仿真分析表明，分析物相对介电常数，即ε3越大时，谐振角度越大。分析物相对介电常数每改变0.01，谐振角度改变0.3度左右。谐振角度极其灵敏，导致SPR技术在生物检测中的广泛使用。

3.3 入射介质(ε1)的影响

在E.Kretschmann配置中，入射介质的变化也会对谐振角度产生影响。

仿真分析不在同入射介ε1=2.25，ε1=3.24以及ε1=5.29时反射系数曲线如图7。仿真表明入射介质相对介电常数越大，表面等离子波谐振角度越小。入射介质相对介电常数改变0.1，谐振角度改变1度左右。

图7 入射介质(ε1)不同时反射系数随入射角变化曲线

3.4 金属介电常数实部和虚部的影响

不同金属或者同一种金属在不同入射光照下，表现为金属相对介电常数(ε2=-Re-j*Im)的变化，通过仿真分析金属介电常数实部和虚部对谐振情况的影响，如图8、图9。

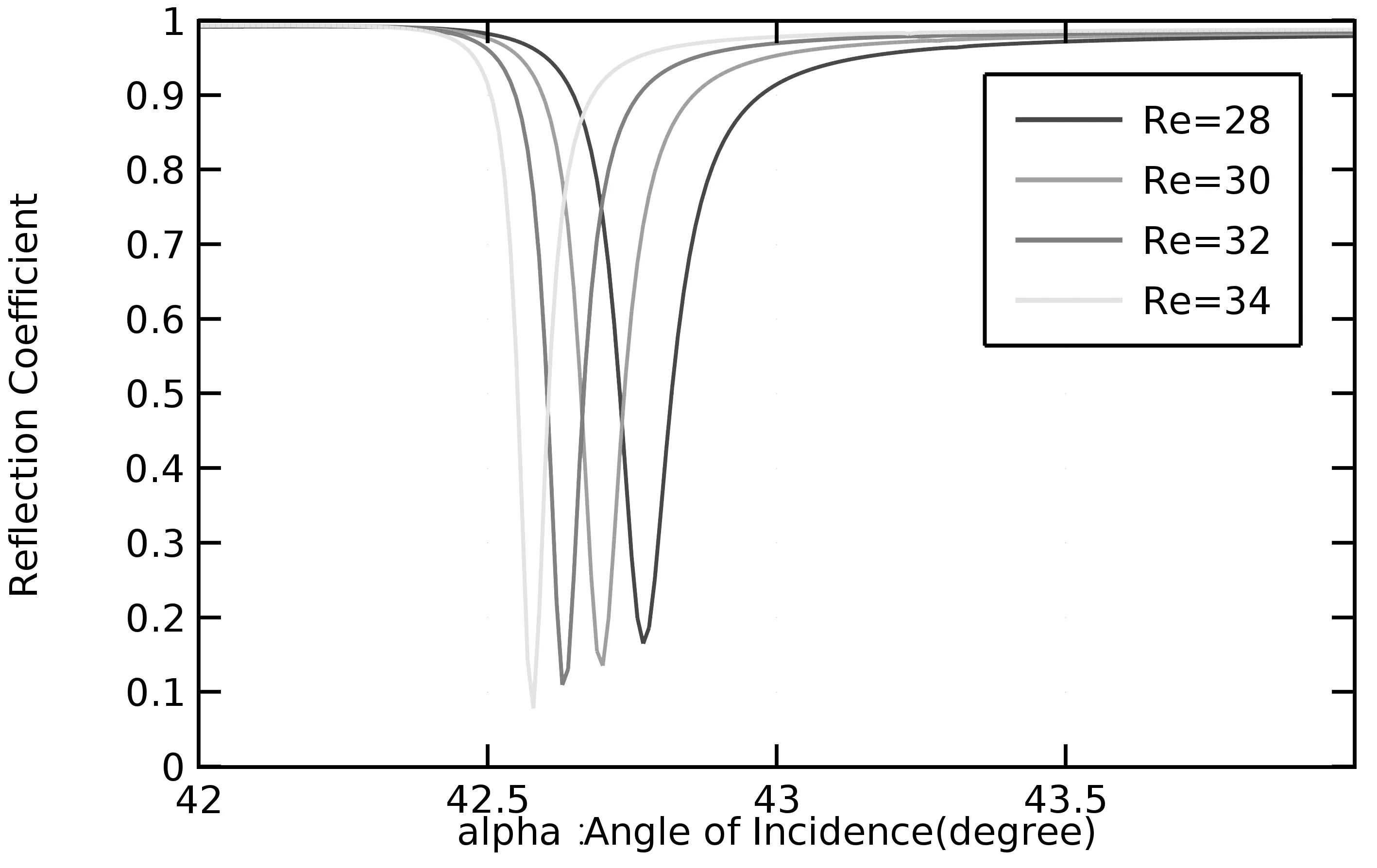
图8 金属实部不同时反射系数随入射角变化曲线图

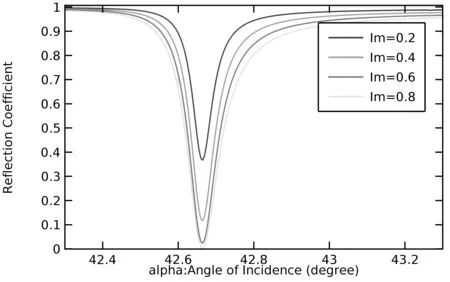
图9 金属虚部不同时反射系数随入射角变化曲线图

仿真表明，实部变化主要影响谐振角度，且谐振角度随实部增加而增加，发射系数随实部的增加而略微增大。虚部变化主要影响谐振时的反射系数，对于谐振角度几乎没有影响，且反射系数随着虚部得增大而增大。金属介电虚部代表金属吸收光的能力，虚部变大，必然会带来损耗的增加，同时也会使传播常数实部一定程度上的减小。由Drude模型和实部虚部分析可以得出，降低表面等离子波传播损耗的方法[9]有：1.降低工作温度，从而降低电子振荡频率。2.提升电子温度，从而提升等离子频率。3.利用增益介质补偿损耗。金属的传播损耗是等离子器件的最大阻碍，如何克服或减小传播损耗成为等离子波导器件的热门课题。

4 结论

本文通过数值仿真，分析在E.Kretschmann配置即介质—金属—介质情况下，不同参数包括入射介质，金属厚度、介电常数，分析物以及入射介质等对表面等离子波谐振角度的影响及其灵敏度分析，进一步体现SPR(surface plasmon resonance)技术在医学诊断、生物检测和环境监测等方面具有极其广阔的应用前景。

[1]Wood R W. On a Remarkable Case of Uneven Distribution of Light in a Diffraction Grating Spectrum[J].Philos Mag Ser 6，1902，4(21)：396-402.

[2]Fano U.The Theory of Anomalous Diffraction Gratings and of Quasi-Stationary Waves on Metallic Surfaces(sommerfeld’sWaves)[J].Journal of the Optical Society of America，1941，31(3)：213-222.

[3]Ritchie R H.Plasmon losses by fast eletrons in thin films[J].Physical Review，1957，106(03)：874.

[4]Otto A.Excitation of Nanradiative Surface Plasma Waves in Silver by Method of Frustrated Total Reflection[J].Zeitschrift für Physik，1968，216(10)：398.

[5]Maier S A.Plasmonics：Fundamentals and Applications[M]. New York：Springer Science & Business Media LCC，2007.

[6]Ahad S L，Sifat A H， Islam M Z.Performance analysis and optimization of Surface Plasmon Polariton based sensing using Kretschmann-Raether configuration with gold layer[C].2015 Annual IEEE India Conference(INDICON)，New Delhi，2015：1-6.

[7]E Kretschmann.The angular dependence and the polarisation of light emitted by surface plasmons on metals due to roughness[J].Optics Communications，1972，(05)：331-336.

[8]黄志洵，姜荣.表面电磁波与表面等离子波[J].中国传媒大学学报(自然科学版)，2011，18(2)：1-13.

[9]陈献.表面等离子波波导的基础研究[D].浙江大学信息学院，2008.

[10]黄志洵.金属电磁学理论的若干问题[J].中国传媒大学学报(自然科学版)，2011，18(4)：1-12.

[11]Ordal M A，Bell R J，Alexander R W.Optical properties of fourteen metals in the infrared and far infrared：Al，Co，Cu，Au，Fe，Pb，Mo，Ni，Pd，Pt，Ag，Ti，V，and W[J].Applied Physics Letters，1985，24(24)：235-237.

[12]Yushanov S P，Gritter L T，Crompton J S，Koppenhoefer K C. Surface Plasmon Resonance[C].Excerpt from the Proceedings of the 2012 COMSOL Conference in Boston，2012.

[13]https：//refractiveindex.info/[DB/OL].

(责任编辑：王 谦)

The Simulation of Surface Plasma Waves

LI Ming-de，LU Gui-zhen，LAN Bing-lin

(College of Electronic Engineering，Communication University of China，Beijing 100024，China)

Introduced the basic concept of surface plasma wave . Then，the surface plasma resonance is excited based on the Kretschmann configuration. The surface plasma is obtained by analytic method and numerical simulation，we also do some study on the metal thickness，dielectric constant，incident medium，analyte media and other parameters for sensitivity analysis by using the numerical simulation，and get some basic laws.

SPW；Kretschmann；sensitivity

TN301.1

A

1673-4793(2017)05-0033-05

2017-05-15

李明德(1994-)，男(汉族)，江西抚州人，中国传媒大学硕士研究生，E-mail：1109268713@qq.com