基于TPML-WMA算法的犯罪率分布模型分析

魏新蕾，颜金尧，陈征，石拓

(1.中国传媒大学信息工程学院，北京 100024；2.中国传媒大学媒介音视频重点实验室，北京 100024；3.中国传媒大学网络中心，北京 100024)

基于TPML-WMA算法的犯罪率分布模型分析

魏新蕾1，颜金尧2，陈征3，石拓1

(1.中国传媒大学信息工程学院，北京 100024；2.中国传媒大学媒介音视频重点实验室，北京 100024；3.中国传媒大学网络中心，北京 100024)

犯罪分布预测问题对社会稳定有积极影响，在学术界引起了广泛关注。现有的研究方法并不能很好的适用于本文所用的数据集。因此，本文构建了矢量运动模型，并提出了一种名为TPML-WMA(Transition Probability Matrix Learning and Weighted Moving Average)的新算法，利用此算法去学习转移概率矩阵，然后对得到的矩阵做加权移动处理，进而来预测未来的犯罪率分布。本文所用数据集是中国某市2001年到2011年共11年间盗窃案发生的数据集，在此之上本文建立了VM(Vector Motion)模型，提出了TPML-WMA算法对犯罪率进行预测，并讨论了不同初始条件下算法的性能。本文还将所提出的算法与基于最小二乘法的经典线性回归方法进行比较。拟合的结果表明TPML-WMA模型的预测性能较线性回归模型有了很大提升。

TPML-WMA算法；转移概率矩阵；加权移动平均；犯罪率分布

1 引言

21世纪是计算机科技迅猛发展的时代，公共安全领域的电子数据信息量也随之膨胀，相关犯罪数据的研究也发展起来。犯罪的发生和地理环境因素是分不开的，所以很多基于GIS系统的犯罪分析应运而生[1]。基于地理位置的犯罪分布问题中的经典解决方案就是建立马尔可夫模型，利用转移概率矩阵来预测分布状态。不过大多数转移概率矩阵都是先验的，利用数学统计方法事先算出来[2]。在国外还有研究团队引入机器学习算法，建立时空模型对犯罪问题进行了一系列的研究工作。在这些文章里，作者是建立网格来划分地理位置，并对每个单元网格贴标签，然后用不同的机器学习算法来计算各个网格的犯罪度，再根据给定阈值进行热点划分[3][4]。也有文章引入自回归积分滑动平均模型(ARIMA)对一个城市连续若干周的案件发生数做预测[5]。陈鹏所在的科研团队曾研究过不同犯罪行为在一天内各自具有何种时间选择特征，何种犯罪类型更具有集中性，然后用聚类方法来比较作案频数曲线来判断哪几种犯罪行为的时间选择特征比较接近[6]。并根据地理位置做加权回归模型来分析犯罪空间分布与地理因素之间的关联，提高影响因素参数估计的准确性[7]。2011年陈鹏等建立时空犯罪热点预测模型，通过描述犯罪主体特征来对下次犯罪地点进行预测，这是从微观犯罪个体角度出发进行的预测[8]。还有一些文章引入区域覆盖加权模型[9]、混合模型时间序列[10]、移动加权平均[11]和支持向量机[12]来预测犯罪。

研究犯罪问题的模型和方法多种多样，但是并不是都能很好的适应本文数据集的特点和研究目的，所以本文提出了基于TPML-WMA算法的模型来解决问题。创新之处在于：

第一，本文对数据集的地理位置按行政区域划分，从整体上关注罪案发生率的分布变化，并考虑了各个区域间的内在影响。

第二，很多成熟的算法并不适用本文的数据集和研究问题，所以本文采用矩阵和向量建立模型，并且将区域间的影响抽象成转移概率矩阵模型，之后本文设计算法代入数据去学习这个矩阵。

我们的研究是以马尔可夫模型为着手点，根据历年的数据通过改进算法来迭代求解转移概率矩阵，然后结合加权移动平均，对学到的九个转移概率矩阵做三项加权移动平均，然后用得到的矩阵做频率分布的预测分析，并且和经典的回归分析做比较。

2 算法分析

2.1 理论模型

在实现TPML-WMA算法之前，本文对数据集建立数学模型。首先本文把研究区域按行政区域划分，记为行政区域1、行政区域2、……、行政区域n。

利用统计分析软件计算出各行政区域对应的盗窃数据案发频率，记为x1、x2、……、xn，如表1所示。

表1 各行政区及其对应的盗窃案发频率

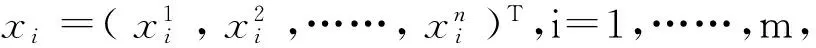
(1)

(2)

对于矩阵Ai，有公式：

(3)

即Aixi=xi+1，i=1，……，m-1

(4)

相邻两年的数据组成一对，m年数据组成m-1对n维的向量，然后代入算法1去学习这个转移矩阵。接下来对学到的m-1个矩阵做三项加权移动平均，加权系数取0.2，0.3和0.5，对矩阵加权移动平均就是对三个矩阵的对应每一个元素做加权移动平均(详见算法2)。最后用得到的矩阵来预测下一年的盗窃案发频率分布。

本文的模型基于两点基本假设：

第一，各个行政区域相互之间不独立，即相互之间的盗窃案发生对其他区域皆有影响。

第二，把某市看成一个封闭系统，市外的盗窃案不会转移到市内；同理，市内的盗窃案也不会转移到市外。简言之，本市内的盗窃案只会在各个行政区域内相互影响和转移。

2.2 TPML-WMA算法

为了对某市各个行政区域的犯罪率分布的相互联系和变化趋势进行量化分析，本文提出TPML-WMA算法。它包括转移概率矩阵学习(TPML)和加权移动平均(WMA)两个主要算法，流程如图1所示：

图1 TPML-WMA算法流程图

其策略如下：

1、清洗数据，统计每一年各区域的罪案发生频率。

2、建立数学模型，每一年各区域罪案发生频率抽象成一个n维向量。

3、上一年和下一年的频率向量之间的转移关系用矩阵表示，满足公式(3)。分别m-1次代入相邻两个频率向量数据，根据TPML算法(算法1)反复迭代得到Ai，i=1，……，m-1。

4、对得到的m-1个Ai，用三项加权移动平均WMA(算法2)来得到最终的转移概率矩阵，用最终的转移概率矩阵作用在最后一年的频率向量上，即得下一年各行政区域的罪案发生频率向量。

5、与经典线性回归算法的预测结果做对比。此处的线性回归是基于最小二乘法的，对每一年的频率向量数据的每一个分量分别做线性回归。

算法 1. TPML

输入：向量对(xi，xi+1)，i=1，…，m-1.

输出：Ai，i=1，…，m-1.

过程：

1：对Ai随机设置初值.

2：xi+1～=Aixi

4：repeat

5： for i=1… m-1 do

6： for k=1…n do

7： for j=1…n do

8： if j=k then

10： else

12： end if

13： end for

14： end for

15： end for

16：until 达到停止条件

算法 2. WMA

Output：A1

Process：

1：repeat

2： for i=1… m-1 do

3： for k=1…n do

4： for j=1…n do

6： end for

7： end for

8： end for

9：until 达到停止条件

经简单计算可知本文的TPML-WMA算法复杂度为O(n3)。

3 案例研究

3.1 数据集

本文使用的数据集是中国某市2001年到2011年共11年间盗窃案数据，属于封闭数据集。本文把前十年的数据作为训练集，第十一年的数据作为测试集，同时，本文为还将TPML-WMA算法的预测结果与线性回归的预测结果做对比。

表2 2001年某市各行政区盗窃案发频率

续表

对于矩阵Ai，仍有Aixi=xi+1，此时i=1，……，9。

3.2 评价标准

本实验采用平均绝对值误差MAE来评价结果，其定义如下：

(5)

3.3 实验及结果分析

我们基于python进行了算法的仿真实验，并与线性回归预测结果进行了对比分析。

实验1：半随机取初始值和初始值固定时对结果的影响

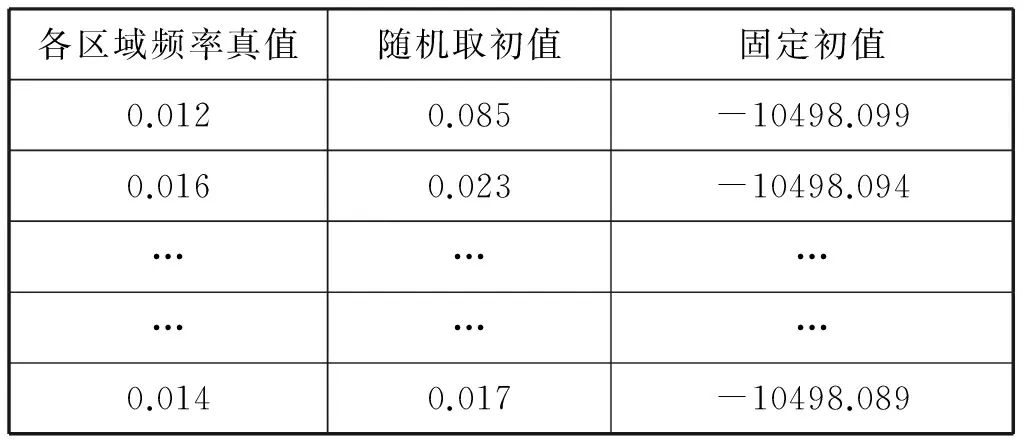
表3 分别半随机取初值和固定初始值后算法得出的各区域频率值对比

实验2：TPML-WMA算法与线性回归的预测结果做对比

由图2可以看出，TPML-WMA算法(红线)和真值(蓝线)整体来说拟合的较好，而线性回归LR算法(绿线)相对拟合的较差，尤其是在区域5、8、10和13。

图2 TPML-WMA与LR预测结果比较

表4给出在平均绝对值误差MAE的评价标准下，TPML-WMA算法的准确性比线性回归算法要高。并且通过对预测结果的求和，TPML-WMA的和基本上仍是1(0.999)，而线性回归的和偏离1的程度就大的多，大约偏离了11%(1.109)。另外，TPML-WMA预测值的加和0.999与1的那一点误差是数值计算中对数的取舍造成的，是不可避免的，这与算法设计无关。所以说TPML-WMA算法的性能比线性回归算法要优越的多。

表4 MAE & SUM结果对比

4 结论

本文中给出的TPML-WMA算法能够很好的描述一个封闭系统内部各部分的频率分布与转移状态。相对线性回归算法而言，用概率转移矩阵来描述各部分状态转移更为贴切，并且由于借鉴了机器学习思路去让矩阵自我学习，这也提高了矩阵的拟合度。

当然目前的研究工作仍然面临很多问题，未来会继续沿着以下几个方向改进：

1、目前的研究成果是基于很多理想的假设条件下得出的结论，真实数据受政治，突发环境影响巨大，不可控的因素很多，如何用数学符号抽象这些不可控因素是研究的难点。

2、本文是针对一个封闭集提出的算法，是否能够在其他公开数据集上很好的应用，还需要继续做实验。

3、对模型的优化工作，比如用矩阵加扰动来抽象不可控因素，或建立开放系统的数学模型等，也需要继续研究。

[1]Yufei Zhang，Huifeng Ji. Using GIS to analyze and forecast the Chinese Crime rate[C].The 2nd International Conference on Information Science and Engineering(ICISE)，2010：3352-3354.

[2]吴绍兵，王昌梅.基于马尔科夫链的民族地区毒品犯罪预测研究[J].计算机与数字工程，2015，43(7).

[3]Chung-Hsien Yu，Max W Ward，Melissa Morabito，Wei Ding. Crime Forecasting Using Data Mining Techniques[C]. 2011 IEEE 11th International Conference on Data Mining Workshops(ICDMW)，2011：779-786.

[4]Chung-Hsien Yu，Wei Ding，Peng Chen，Melissa Morabito. Crime Forecasting Using Spatio-Temporal Pattern with Ensemble Learning[C]. The 20th Pacific Asia Conference on Knowledge Discovery and Data Mining(PAKDD)，2014：174-185.

[5]Peng Chen，Hongyong Yuan，Xueming Shu. Forecasting Crime Using the ARIMA Model[C].The 5th International Conference on Fuzzy Systems and Knowledge Discovery(FSKD)，2008，5：627-630.

[6]陈鹏，疏学明，颜峻，等.犯罪活动在一天内的发生时间规律[J].清华大学学报(自然科学版)，2009，49(12)：2032-2035.

[7]颜峻，疏学明，袁宏永.盗窃犯罪空间分布与地理因素的关联[J].清华大学学报(自然科学版)，2010，50(2)：174-186.

[8]陈鹏，疏学明，袁宏永,等.时空犯罪热点预测模型研究[J].系统仿真学报，2011，23(9).

[9]薛钟，乔良，王峰等.连续犯罪预测的区域覆盖加权模型(AOWM)[J].数学实践与认识，2010，40(15)：212-217.

[10]涂小萌，陈强国.基于ARIMA_LSSVM混合模型的犯罪时间序列预测[J].计算机技术与应用，2015，41(2).

[11]王璟瑶，秦静，刘军.犯罪案件移动平均预测模型改进研究[J].中国人民公安大学学报(自然科学版)，2015，(1).

[12]陈鹏，胡啸峰，陈建国.基于模糊信息粒化的支持向量机在犯罪时序预测中的应用[J].科学技术与工程，2015，15(35).

(责任编辑：王 谦)

AnalysisofCrimeRateDistributionBasedonTPML-WMA

WEI Xin-lei1，YAN Jin-yao2，CHEN Zheng3，SHI Tuo1

( 1． Information Engineering School，Communication University of China，Beijing 100024，China; 2． Key Laboratory of Media Audio & Video，Communication University of China，Beijing 100024，China; 3． Computer NIC Center，Communication University of China，Beijing 100024，China)

Crime distribution forecasting has a positive impact on social stability and has drew much attention in academia. Existing research methods are not applicable for specific data sets very well，such as the data in this paper. So we build the Vector Motion Model and propose a new algorithm named as TPML-WMA(Transition Probability Matrix Learning and Weighted Moving Average algorithm)to predict a future robbery distribution and figure out how it transfers. We let the transition probability matrix to learn by itself，and do the weighted moving processing on the matrices. Using crime data from 2001 to 2011 from some city in China，we set up the model，propose TPML-WMA algorithm to predict the crime distribution，then discuss the performance of algorithms under different initial conditions. At the same time，we compare the proposed algorithm with the classical linear regression method based on the least square method. The results illustrate that the prediction performance of TPML-WMA is greatly improved compared with the linear regression method.

TPML-WMA algorithm；transition probability matrix；weighted moving average；crime rate distribution

TP399

A

1673-4793(2017)05-0021-06

2017-07-05

魏新蕾(1981-)，女(汉族)，吉林梅河口人，中国传媒大学博士研究生.E-mail：weixinlei@cuc.edu.cn