“问”有学问方能出“彩”

周玲娇

[摘 要]追问是课堂教学的有效手段之一，但需要问得有技巧。在学生似有所悟、出现错误，或遇到教学的重难点时巧妙进行追问，可启迪学生的思维，使其思維走向更深处，让课堂更精彩。

[关键词]追问；技巧；精彩课堂；错误；难点

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）29-0058-02

追问是数学课堂教学的重要手段，更是精妙的教学艺术。要使追问有效，教师应抓住追问的时机，抓住课堂中转瞬即逝的契机及关键点，适时追问，使课堂教学形成思维交锋、智慧启迪、心灵碰撞的良好态势。如，在知识难点处或学生思考浅显、出现错误、矛盾困惑时追问，可促进学生深入思考，激活学生的思维，进而让课堂更高效。

一、于思考浅显处追问——深入思考

著名教育家第斯多惠曾说：“教学的艺术不在于传授本领，而在于激励、唤醒、鼓舞。”学生由于心智尚未健全，对问题或知识点的思考往往比较粗糙、缺乏深度，不能进行深层次的思考，这就要教师把握时机，进行深层次追问，在学生思考浅显处牵一牵、引一引，诱导学生思考、探索和想象，促使其思维从表面走向深刻。

例如，教学“9+4”时，我设计这样的环节：

师：请说说你是怎么想的？

生（手指着4）：对于9+4，把4分成1和3，将分出来的1和9相加，得到10，接着和剩下的3相加，等于13。

师：为什么要把4分成1和3呢？

生：为了把9凑成10。

师：哦，是为了凑成10。你真会思考，真棒！这种方法我们就把它叫作“凑十法”，它能降低计算的难度，让我们算得又快又准！

针对学生浅显、形象的思维表象，教师进行适当的追问，可将学生的思维引向深处，促进深入思考，从而发现知识的本质。本案例中，教师追问“为什么要把4分成1和3呢”，诱导学生说出拆分的目的，紧接着，教师带领学生进行总结，得出解决问题的一般方法——凑十法。这样教学，学生对“凑十法”的理解和掌握就更为扎实、到位，这也正是追问的魅力所在。

二、于出现错误时追问——巧妙纠正

著名的哲学家波普尔说过：“错误中往往孕育着比正确更丰富的发现和创造因素，发现的方法就是试错的方法。”教学也是如此。教师要敢于直面学生的错误，分析学生出错的原因，甚至是欣赏错误中的“美丽”。教师适时的追问可让学生发现错误、议错、辩错，通过这一动态过程，学生对知识和技能的掌握将更加牢固。

例如，教学“平均数”时，出示：实验小学跳绳队教练准备从队员李军、张明、陈刚中挑选一人参加比赛，下表是最近5次训练中这三名队员每分钟跳绳的成绩统计情况（“/”表示没参加本次训练）。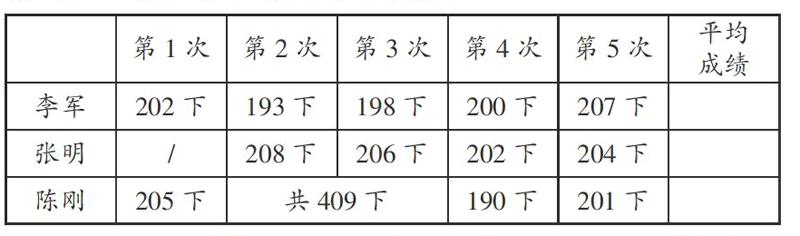

师：如果你是跳绳队的教练，你认为应该怎样选？

生1：由于张明没参加第1次训练，如果比较总成绩的话不公平，我认为应该比较平均成绩，谁的平均成绩高就选谁。

师：他们的平均成绩各是多少？

生1：李军的平均成绩是（202+193+198+200+207）÷5=200（下），张明的平均成绩是（208+206+202+204）÷5=164（下）。

（教师没有马上评价，而是引导学生讨论）

师：张明参加了5次训练吗？

生2：没有，张明没参加第1次训练，对应的只有4次成绩，所以应该除以4，结果是205下。陈刚的也只有4次成绩，所以他的平均成绩是（205+409+190+201）÷4≈251（下）。

生3：不对，陈刚的平均成绩应该是（205+409+190+201）÷5=201（下）。虽然只有4次成绩，但陈刚实际上一共跳了5次，所以应该除以5。

生2（恍然大悟）：我明白了。

师（顺势追问）：平均数应该怎样求呢？

生4：用总数除以份数就可以求出平均数。

该案例中，教师巧妙追问，如“他们的平均成绩各是多少”“张明参加了5次训练吗”，逐步引导学生深入思考，暴露学生的错误，使学生自主发现求平均数的关键因素。由此可见，教师要适当追问，以追问过程中出现的“错误”为媒介再追问，诱发学生产生不同见解，激励学生主动参与问题的探究过程，让学生经历观察、操作、思考、讨论和辨析，自主纠正错误。学生对错误的印象越深刻，纠正错误之后对知识的掌握就越牢固。

三、于知识难点处追问——画龙点睛

小学生的认知水平和生活经验是很有限的，而数学的知识点具有抽象性，学生理解起来存在一定困难。这些知识点是教学的难点与关键所在，教师可通过追问的方式为学生铺好思维的跳板，引导学生在更高层次上进行有效思考，从而深入理解数学知识。

例如，教学“认识分数意义”时，我设计这样的环节：

师：把6本练习本平均分给2人，每人分得几本？

生1：每人分得3本。

师：把8本练习本平均分给2人，每人分得几本？

生2：每人分得4本。

师：把一叠练习本平均分给2人，每人分得多少？

生3：每人分得这叠练习本的■。

师（追问）：这里的“■”代表什么？

生3：这叠练习本的一半。

师（追问）：结果为什么不是具体的数呢？

生3：因为不知道这叠练习本究竟有多少本。

师（继续追问）：那么6本练习本，平均分成2份，每一份也可以用■表示吗？

生4：可以。

师：8本练习本，平均分成2份，每一份还可以用■表示吗？endprint

生5：可以。

师：一个的结果是3本，一个的是4本，数量不同，为什么都可以用■表示呢？

生6：因为■表示的都是将总数平均分为2份后的其中1份。

师：对，要弄清楚谁是整体，整体不同，所对应的具体数量也就不同。假如把100支铅笔平均分成2份，每一份可以用■表示吗？

生7：可以，无论整体是多少，只要平均分成2份，其中的1份一定是整体的■。

师：是■支吗？

生8：不是，■在这里表示的是总数的一半，而不是具体的数量。

学习分数的产生时，学生很容易理解“不能用整数表示的，则用分数来表示”，但却不能理解“把许多物体看作一个整体”这一教学难点和关键点，往往将一个整体被平均分后每份的占比与具体的数量混作一谈。而上述案例中，教师巧妙地进行追问，如“那么6本练习本，平均分成2份，每一份也可以用■表示吗？”“一个的结果是3本，一个的是4本，数量不同，为什么都可以用■表示呢？”等问题，启迪了学生的思维，帮助学生深刻理解分数的意义。在这里，我们可以看到，学生顺着教师的引导，实现了知识的内化，而且在整个过程中，每位学生均兴趣盎然，获得了成功的体验，培养了数感，实现了自我完善与自我发展。

四、于矛盾困惑处追问——茅塞顿开

在自主学习、独立思考和讨论交流的过程中，学生的思维可能会遇到障碍，出现卡壳现象，这便需要教師及时追问，让学生在境中思、在思中悟、在悟中得，以此提升思维层次，加深对知识的理解。

例如，教学“垂直与平行”时，我设计这样的环节：

师：请同学们仔细观察上面6组图形，如果要给它们分类，你会怎么分？

生1：②③一类，①④⑤⑥一类，因为②③是有交叉的，而①④⑤⑥是没有交叉的。

师：②中的图形是怎样得来的呢？请你通过手势表示一下。③的呢？像②③这样两条直线互相交叉的现象，在数学上叫作相交。现在我们可以说②③中的两条直线分别相交。

师：①④⑤⑥中的两条直线现在均没有相交，它们是不是永远都不会相交呢？

生2：我的分类是②③、⑤⑥、①④，因为我觉得⑤⑥中的两条直线在某一处是相交的。

师：那么它们怎样才会相交呢？

生2：只要将直线延长一些就可以了。

师：在⑤中，要延长哪一条直线呢？

生2：直线a。

师：延长a吗？为什么？

（师延长直线a，得到直线a、b相交）

师：看来⑤确实也属于相交。那⑥呢？

生3：⑥中的两条直线都延长，最后也相交。

师：你是如何确定的呢？如果⑥中的两条直线均已到达纸张的边缘，还可以继续延长吗？

生3：可以。假设这张纸可以无限延伸，因为平面是无限大的，这样就能继续延长直线。最终发现，⑥中的直线a、b相交。

当学生遇到困惑时，教师应将时间让渡给学生，等一等，让他们自己想办法解惑、证明，自主建构新知。此时，教师利用“如果要给它们分类，你会怎么分？”“①④⑤⑥中的两条直线现在均没有相交，它们是不是永远都不会相交呢？”“那么它们怎样才会相交呢？”等问题引导学生的思维方向，巧妙地激活学生的思维，使之亲历知识的形成过程，从而知其然且知其所以然，使课堂既具有广度又有深度。

数学是理性的，教师是理性的引导者，不断追问着；学生是理性的学习者，不断追寻着！陶行知说过：“行是知之路，学非问不明。”教学中，教师不仅要有追问的意识，善于倾听和思考学生的回答，还要把握好追问的时机与方向，使课堂因“问”而精彩！

（责编 吴美玲）endprint