小学数学模型思想的渗透策略
2017-12-11谢石月
谢石月
[摘 要]模型思想是数学思想中的重要思想之一,尤其是在“数与代数”教学中,模型思想的思维过程是理解数理和问题解决的重要途径,又特别是数量关系、数学公式和数学规律等内容,都蕴含着了丰富的数学模型思想。渗透模型思想和发展学生的模型思维是小学数学课堂改革不可忽视的教学使命。以一年级上册“减法”的教学片段为例,阐述“表象——抽象——内化——建模”四步式渗透模型思想的教学策略。
[关键词]减法;模型思想;渗透
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2017)29-0026-02
《义务教育数学课程标准(2011年版)》指出“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径”。模型思想作为10个核心概念之一,并首次被以“数学基本思想”作为“四基”之一提出,足以证明其在数学教学中的地位和重要性。史宁中教授在《数学思想概论(第1辑)》中指出:“至今为止,数学发展所依赖的思想在本质上有三个: 抽象、推理、模型,即抽象是核心,推理是得到数学发展的重要过程,而通过模型建立数学的联系则是不可缺少的环节。”由此可见,模型思想的渗透在学生学习数学和发展数学素养中有举足轻重的作用。
“数学模型, 一般是指用数学语言、符号或图形等形式, 来刻画、描述、反映特定的问题或具体事物之間关系的数学结构, 它是对客观事物的一般关系的反映, 也是人们以数学方式认识具体事物、描述客观现象的最基本的形式。”研究表明,数学模型有几个特点:首先,模型的建构需要以现实问题或具体情境为依托;其次,模型的建构过程需要运用抽象思想;再次,对模型的理解和解释需要渗透符号化思想及科学的数学内涵表述。
教学实践表明,数学模型的建构和运用对学生认识数学知识、理解数学本质和发展学生的思维能力有重大的意义。模型的建构和模型思想的渗透不同于数学知识的简单交待,它的实施过程具有“隐蔽性”和“间接性”,不能靠机械生硬的说教,而要让学生以经历、体验、感悟和内化为主,经历信息处理、抽象与概括、数学表达、模型验证和模型应用等环节,以“渗透”为基调,即“表象—抽象—内化—建模”四个步骤。
[教学片段]
师(出示情境图):谁来说一说你从第一幅图中看到了什么?
生1:我看到小丑手上有4只气球。
师:第二幅图呢?
生1:第二幅图中有1只蓝色的气球飞走了,还剩下3只红色的气球。
师:你能把两幅图连起来说一说吗?
生1:小丑手上有4只气球,飞走了1只,还剩下3只。
师:你能根据这两幅图提出一个数学问题吗?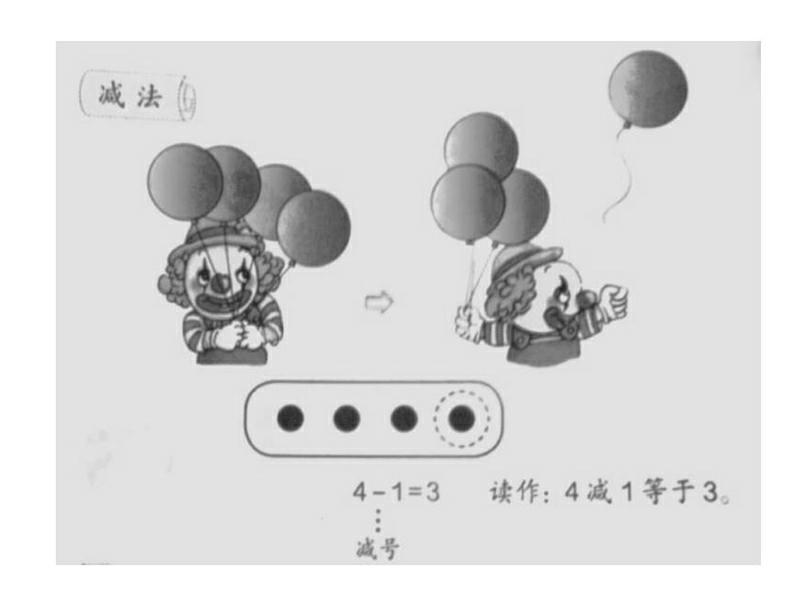
生1:小丑手上有4只气球,飞走了1只,还剩下几只?
生(齐):3只。
师:太棒了!你能用圆片代替气球,动手摆一摆这个过程吗? (学生对照情境图摆圆片)
师:小丑手上有4只气球,飞走了1只,还剩下3只;从4张圆片中拿走1张,还剩3张,都可以用同一个算式“4-1=3”来表示。(板书:4-1=3)
师:谁来说一说这里的“4”表示什么?“1”表示什么?“3”又表示什么呢?生活中还有许许多多这样的数学问题,“ 4-1=3”还可以表示什么呢?请同桌互相说一说。
一、建立表象——模型思维的孕育
小学生的思维以直观形象为主,现实生活、具体情境和形象直观的图像可以让学生的思维起点靠近其思维的最近发展区,让学生快速确立思维起点。数学模型的建构实际上也是一种数学思维的发展。思维的产生和发展起源于学生丰富的数学表象,而数学表象的积累则大多依靠直观形象,因此,数学模型思想的孕育必须将数学问题置于生动有趣的情境之下,诱发学生的认知欲望,为引导学生发现和解决问题,激发学生更深入的思考奠定基础。在教学片段中,教师将减法数学问题建立在气球由多变少的情境中,让学生观察情境图后说一说从第一幅图中看到了什么,从第二幅图中又看到了什么。学生在解读情境后找到数学信息,并对信息进行加工:从第一幅图中看到小丑手上有4只气球;从第二幅图中看到有1只气球飞走了,剩下3只气球。
有了表象,才能使心理活动得以进一步的深入,才能再现已有的认知信息,才能将已有经验与新的数学现象进行沟通和联系,激发和孕育新的思维。气球由多变少的情境既让学生感知到现实中的数学现象,又能让学生初步感悟数量的变化,为数学模型的建构积累了充足的数学表象。研究表明,记忆要经历识记、保持、重现和再认四个过程,因此数学表象的建立大致有几个步骤,即发现—想象—重现—调整。在此过程中,学生通过观察情境,在教师的引导下运用信息进行想象并描述数学现象,然后在教师的引导下不断调整和完善,模型思维逐步形成。
二、抽象问题——模型思维的萌发
数学表象是数学模型建立所依托的素材和基础,对学生而言,在积累了充分的数学表象之后,还要从所积累的数学表象体现出来的数学信息中提炼和抽象出数学问题,为问题的解决提供思维方向和目标。如教学片段中,教师把抽象问题的任务抛给学生:“你能根据这两幅图提一个数学问题吗?”其目的就是让学生的思维能从具体的情境中过渡到数学问题,这是从形象到抽象的过程,更是模型思维的萌发时机——这是求“剩下几个”的问题。有了问题的指引,学生也就有了学习的目标和方向,这样学生才能在数学问题的驱动下,经历问题的发现、探究、解决等一系列思维活动,因为有效问题的提出,除了可以让学生体验到解决问题的步骤、思路和策略,感受探究带来的喜悦外,还可以让学生在解决问题的过程中,通过与同伴的思维交流和互动,感受解决问题方法的多样性和策略多样性。可见,在模型思想的渗透教学中,在学生充分感受了数学情境后,要有一个“去情境化”的思维过程,因为情境创设的最高境界就是“去情境化”,即起于情境但又高于情境,是让学生有效地由形象直观抽象出数学问题,为学生深入探究数学模型提供指引。endprint
三、内涵表述——模型思维的内化
数学符号是一种特殊的数学语言,是数学学习不可缺少的工具,用数学符号对数学过程、数量关系和变化规律进行表述,是对数学表象的进一步解释,是对数学信息的加工和分析,是数学探究的必由之路。符号的运用可以让学生从个别数学现象过渡到一类数学现象,是从个性到共性的过程。
王永春在《小学数学与数学思想方法》一书中指出:“数学模型是用数学语言概括地或近似地描述现实世界的特征、数量关系和空间形式的一种数学结构。”对于数学模型来说,模型的建构其实就是对一种特殊的“数学结构”的理解和发展,而对这种“结构”的认识离不开数学符号对数学过程的科学表述,这种内涵的表述就是一个思维的过程。如教学片段中,教师有意识地对学生进行了“符号思想”的渗透——你能用圆片代替气球,动手摆一摆这个过程吗?适时地引导学生用圆片替代气球,能让其重新体验“数量减少”的过程,再次积累数学表象,积累模型建构的思想。教师采取情境启发和操作体验,让学生在“气球飞走”和“圆片移走”的情境下,把物(气球和圆片)分别抽象成数字(4、1、3),引导学生用数学语言去描述这种数学现象:有4只气球,飞走了1只,还剩下3只;有4张圆片,拿走1张,还剩下3张,这种数学变化都可以用同一个算式“4-1=3”来表示——这就是建模。在这个过程中,学生亲历了符号的运用过程,这也是学生寻找特征和共性的过程,是对从个别算法引向共性的算理的感悟和理解,更是思维的一次飞跃。
四、应用和拓展——模型思想的建构
经过“表象——抽象——符号——内化”的过程,数学模型“4-1=3”悄然在学生的思维中成型,但它在学生的思维里还只是一个模糊的“结构”,这个特殊的结构还需要有足够的发散思维去印证和充实。这时,只有对模型的意义进行“再认知”,才能让模型思想成为学生的主动思维习惯,并在将来的数学学习中将其应用和发展。如在教学片段中,教师在得出了“4-1=3”后,继续让学生结合情境说一说“这里的“4”表示什么?“1”表示什么?“3”又表示什么呢?”目的是让学生深入感受“总数”“部分数”和“剩下”的意义,并理解它们三者之间的数学本质联系和意义。这时将数学生活化,让学生结合生活经验,发散个性思维,说一说“生活中还有许许多多这样的數学问题,‘4-1=3还可以表示什么呢?”学生就能提出:“树上有4只小鸟,飞走1只,还剩3只。” “我有4个苹果,吃了1个,还剩3个。”……
“还有哪些数学问题可以用‘4-1=3表示呢?”教师的追问绝对不是简单、机械、生硬的重复,而是基于学生学习数学的特点——模型思维需要由具体、形象开始,借助操作予以内化和强化,依托思维发散和思维联想加以扩展和推广。这种思维发散和思维联想将赋予“4-1=3”以更丰富的“模型”意义,有利于促进和加强学生对数学模型的理解,拓宽学生的数学思维,也有利于巩固模型的应用和发展学生的模型应用意识。
唐代诗人杜牧说过:“学非探其花,要自拔其根。”这里的“根”指的就是数学思想与方法,它和“授之以鱼,不如授之以渔”的教育理念有异曲同工之处,因为它是数学的精髓和灵魂。数学的教学不仅要注重对显性数学知识的认知和理解,作为“四基”之一的数学思想方法更加不容忽视,当今乃至未来的数学课堂都应注重激发学生更多的思考,渗透更多的思想方法,让学生真正成为“智慧型”的学生而不是单纯的“知识型”学生。
[ 参 考 文 献 ]
[1] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2011.
[2] 史宁中.数学思想概论(第1辑)[M]. 哈尔滨:东北师范大学出版社,2008.
[3] 王永春.小学数学与数学思想方法[M]. 上海:华东师范大学出版社 ,2014.
(责编 金 铃)endprint
