凸显概念本质 培养问题意识

葛秀兰

[摘 要]“以学生为主体”是当下课堂教学的追求，问题意识的培养是学生核心素养形成的重要途径。以“圆的认识”的教学为例，从学生的需求出发，观察、理解、发掘学生，在新舊知识的衔接处、在重难点的困顿处、在思维的疑虑处，给予适当的点拨和引导，凸显概念的本质，使学生的思维通道顺畅，问题意识增强。

[关键词]圆的认识；问题意识；数学生长；概念本质；思维发展

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）29-0022-02

“问题意识”并不仅仅是简单的提出问题和解决问题，它还是人们对客观事物做出自觉反应的心理过程，是揭示问题本质的发现过程，是研究和发现问题的动态过程。近年来，我根据课堂问题多、散、浅的现象，提出了“增强问题意识，提高课堂实效”的研究主张，将目光聚焦于“教什么”“为什么教”“学什么”“学得怎么样”。现就“圆的认识”教学实践为例谈谈我的做法。

一、直击课堂本貌，着眼问题孕伏

近期，我先后听了三位教师执教“圆的认识”这节课。通过对比，发现教学流程大致相同：寻圆，比较圆和其他平面图形的区别；画圆，认识圆的各部分名称；探圆，理解圆的本质特征；赏圆，体会圆在生活中的应用。教学过程中，学生的学习兴趣、状态、收获，令旁观者欣慰，但是，学生的提问和教者的解答引起了我的注意和思索。第一，在自学圆各部分名称这个环节，学生对半径和直径的意义的表述并不尽如人意，究其原因，是学生不能真正理解圆的概念的内涵。另外，在自学以后，有学生提出疑问：“圆心通常用字母 O来表示，有没有不通常的情况？”教师告诉学生这是人们长期以来约定俗成的。这样浅层次的回答显然无法培养学生的问题意识，会让学生止步于“数学探究之门”，沦为机械而又被动的“概念接收机”。第二，在动手折一折、画一画、量一量发现圆的半径和直径关系的环节中，有一位学生量得半径为2.1厘米，直径为4厘米，所以他只能勉强得出直径是半径的2倍的结论，教师用“测量有误差”给他解了围。测量有误差的简单结论，是教师在已有的半径与直径关系的基础上的判断，苍白无力的说辞，显然不足以解除学生内心的疑惑。第三，在比赛画圆的半径，看谁画的多，从而证明圆有无数条半径的环节，学生看似学得轻松，但是如果站在数学教学的新高度，真正给予学生问题意识的供养，那就需要教师把课堂打开，发展学生的数学思考力，为学生问题意识的生长而教。

二、直面教学本真，着意问题萌生

“本真”意味着天然去雕饰的质朴纯粹，也意味着个性率真的自然表露。对教学本真的追求，则应从儿童立场出发，凸显“为学生而教”的教学价值观，剔除哗众取宠，还学科教学以本来面貌。对于“圆的认识”这节课，很多时候教师喜欢用精美的画面和唯美的意境，令学生对圆心驰神往，而本真课堂的回归，需要学生通过学习和体会，真正感悟圆来自于它最为数学本质的美丽。因此，教学环节应紧紧围绕圆的本质特征，引导学生自主探究、合作交流、质疑争辩，发展学生的数学思维，让学生的数学问题意识能够拥有萌芽的土壤。

【教学片段1】师（出示：“一切平面图形中，圆是最美的。”）：通过这节课的学习，你觉得毕达哥拉斯对圆有怎样的认识，才能总结出这样的结论？

生1：圆有无数条对称轴。

生2：圆有无数条半径，无数条直径。

生3：在一个圆内，所有半径都相等，所有的直径也都相等。

生4：圆心到圆上任意一点的距离都相等。

师：正因为圆有这些特征，所以圆看起来饱满、匀称和光滑，非常美，在日常生活中圆的应用也很广泛。

师（出示自行车车轮图片）：车轴为什么装在圆心处？自行车轮为什么做成圆形？

生5：这样平稳，如果是正方形，就会颠簸。

师：为什么这样平稳？

生6：圆心到圆上任意一点的距离都相等。

三、追溯情境本源，着力问题驱动

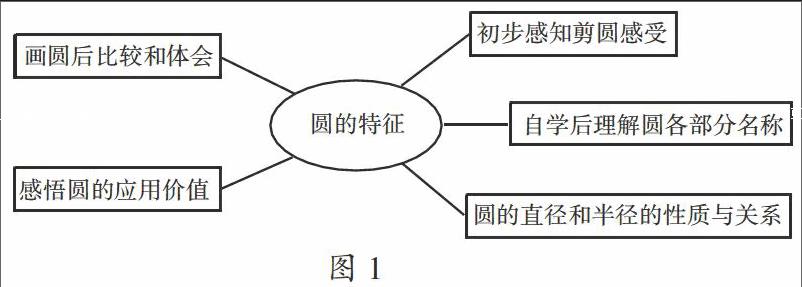
圆，学生是熟悉的，“曲边围成的，没有棱角的”是他们早有的知识经验，也是圆的直观特征。圆的本质特征“平面内，到定点的距离等于定长的点的集合”，对学生而言不仅陌生，而且隐性、抽象。什么样的问题能催生学生强烈的好奇心与求知欲，主动探寻圆的本质特征？在这样的思考之下，我进行了如下设计：（1）引导学生比较用不同方法画圆的共同点；（2）要求学生用圆规在规定时间内画圆以后，思考“你画的圆这么好、这么圆，是怎么做到的？有什么秘诀？”（3）思考“什么是圆的半径？什么是圆的圆心？什么是圆的直径？”（4）你觉得毕达哥拉斯为什么说“一切平面图形中，圆是最美的”？

如图1，围绕核心问题“什么是圆的本质特征和性质？”而设计的问题串，不但能将学习任务变为学生自己的问题，而且能让学生的思考指向探究圆的本质特征，让学生的问题意识得到滋养。

【教学片段2】师（在研究圆的半径和直径的性质过程时）：动手画一画、折一折、量一量，你能发现什么？

师：想一想，有没有其他办法也能够发现圆的直径和半径的关系？

生1：在画圆时我发现同一个圆的半径都相等，如果不相等就画不了圆。

师（和学生合作演示画圆的过程）：如果有一条半径不相等，圆就会有缺口，就不圆了。

生2：圆的半径是圆心到圆上一点的线段，而直径是过圆心，且两端都在圆上的线段，直径的长度等于两倍半径的长度。

“有没有其他办法也能够发现圆的直径和半径的关系？”这个问题让学生的思考与之前的操作联系起来，学生的思维由直观感知逐步向抽象认知过渡，对圆的本质特征认识更加深刻，在此过程中学生的空间观念自然得以培养。

【教学片段3】师：自学课本后，你有什么疑问？

生1：圆心通常用字母O来表示，有没有不通常的情况？

生2：也可以用其他字母表示，用字母O表示圆的圆心只是约定俗成而已。endprint

师：是的，字母A、字母B等都可以表示一个圆的圆心，但不管用什么字母表示，它们表示的意义都是一样的。你知道什么是圓的圆心吗？

生3：圆的中心。

师：你知道什么是圆的中心吗？

生4：到圆上任意一点的距离都相等的点。

生5：画圆时的定点。

学生在经历自学活动之后，就会产生不同的想法，并提出符合学生年龄特点和认知水平的问题。事实上，在以后的学习中，学生会遇到圆A、圆B等情况，包括将圆心画在直角坐标系的O点处，都和学生提出的问题有关。因此，学生的问题意识只要得以鼓励和催生，学生思维的火花就会被点燃。

四、彰显“让学”本位，催生问题内化

“让”是一种立场，以学生发展为本；“学”是一个历程，以自主探究为要。学生学习数学的过程，既是教师引导下的意义建构过程，也是在自身需求发展中自主建构的过程。荷兰数学家弗赖登塔尔提出“学一个活动的最好方法是做”。通过“做”能让学生进行“再创造”，从而获得知识，形成素养。

【教学片段4】师：你能用身边的工具（硬币、笔、量角器、圆规、绳子）画一个圆吗？

生1：可以沿着硬币的边缘画一个圆。

生2：也可以用圆规画。

生3：还可以用量角器先画出圆的一半，然后再画出另一半。

师：我要在黑板上画一个更大的圆，怎么画？

生4：可以用木头固定一根绳子的一端，拉直绳子，另一端绕着这端旋转一周。

（师生合作，用一根绳子在黑板上画圆）

师：画圆后你有什么感受？有什么建议？

生5：用圆规画圆时，针尖不能动，两脚间距离不能变。

生6：用圆形物体画圆时，要按住圆形物体不能动，沿边缘描一圈。

师：谁能说一说这几种画圆的方法有什么共同的地方？

师：画圆时，首先固定一条线段的其中一个端点不动，然后将另一端点绕这一端点旋转一圈。

通过画圆的活动和交流的过程，学生对画圆的两个关键——“定点”和“定长”的理解逐步深入，教师再引导学生用圆规画圆并总结画圆的经验，就能使学生的对圆的本质特征的认识更进一步，为学生后面自主学习（圆的各部分名称）、逻辑推理（圆的半径和直径的性质与特征）和问题意识的培养提供了支撑。

五、尊重求知本心，着陆问题深化

学生在画圆的基础上已经能够初步领会圆的半径和直径的含义，但是用数学语言来表达还十分困难。语言是思维的外壳，怎样的语言才有利于学生理解，有利于学生独立思考，有利于学生获取真正的知识呢？教师要能尊重求知本心，在“让”和“引”之间游刃有余，在不露痕迹中使学生的数学思维得到发展，才能使他们的问题意识得以增强，数学素养得以提升。

【教学片段5】师：什么是半径？

生1：半径是对称轴的一半。

生2：把圆对半切开，切口的线段的一半就是半径。

师：请上来指一下哪一段是半径。

师：半径是直线还是线段？

生3：线段。

师：这条线段的一端在哪？另一端在哪？

生4：一个端点是圆心，另一个端点在圆上。

师：谁来说说什么是圆的半径？结合刚才画圆的感受，圆心和半径跟画圆时的什么有关？

生5：圆心就是画圆时针尖固定的那一点，半径就是画圆时圆规两脚间的距离。

师：圆心就是我们刚才所说的定点，半径就是定长。

深入思考学生提出的问题，显然，学生数学核心素养的发展是有阶段性和关联性的。因此，问题意识的培养，需要教师立足教学本真，需要教师用自身的专业素养，脚踏实地地去打开一扇扇数学素养之窗，帮助学生随时发现意外的通道和美丽的风景，这也是我们今后一段时间内坚持的方向。

（责编 童 夏）endprint