基于拉普拉斯变换的二阶系统传递函数的参数研究*

江立辉，牛 欣，汪 冉，汪 成

(1.合肥学院数学与物理系，安徽 合肥 230601；2.合肥学院机械工程系，安徽 合肥 230601)

基于拉普拉斯变换的二阶系统传递函数的参数研究*

江立辉1，牛 欣1，汪 冉1，汪 成2

(1.合肥学院数学与物理系，安徽 合肥 230601；2.合肥学院机械工程系，安徽 合肥 230601)

为了研究二阶系统传递函数中固有频率和阻尼比这两个参数，运用牛顿第二定律构建微分方程数学模型，并利用拉普拉斯变换理论，说明了传递函数中的固有频率和阻尼比这两个重要参数表达式的正确性和合理性.从固有频率和阻尼比的实际含义出发，对它们的计算公式进行详细证明，从而加深对二阶系统传递函数参数的理解，并将其更好地运用到实际问题中.

二阶系统；传递函数；固有频率；阻尼比；拉普拉斯变换

引言

二阶系统是控制系统的一种基本组成形式，在实际问题中，二阶系统的典型应用极为普遍[1～3].因此，对二阶系统进行研究具有较大的实际意义.而在二阶系统的传递函数中，有两个极其重要的参数即为固有频率ωn和阻尼比ξ.只要分析固有频率ωn和阻尼比ξ的值的大小，就能较方便地求得任何二阶系统的动态性能.但是现有的教材以及相关的资料是直接给出了这两个参数的计算公式，并未结合参数的实际意义对公式的正确性与合理性进行说明，因此初学者会对这两个参数的表达式的给出感到突兀，从而无法深入理解固有频率ωn和阻尼比ξ对二阶系统的影响.

本文从固有频率ωn和阻尼比ξ的基本含义出发，建立相应的数学模型，运用拉普拉斯变化的知识[4～5]，证明了这两个参数公式的正确性和合理性，从而促使初学者更进一步地理解这两个参数.

1 问题的引入

较常见的二阶系统模型为质量块-弹簧-阻尼器模型，而其他的二阶系统模型与其本质相同，因此在二阶系统的推导中采用质量块-弹簧-阻尼器模型，如图1所示.

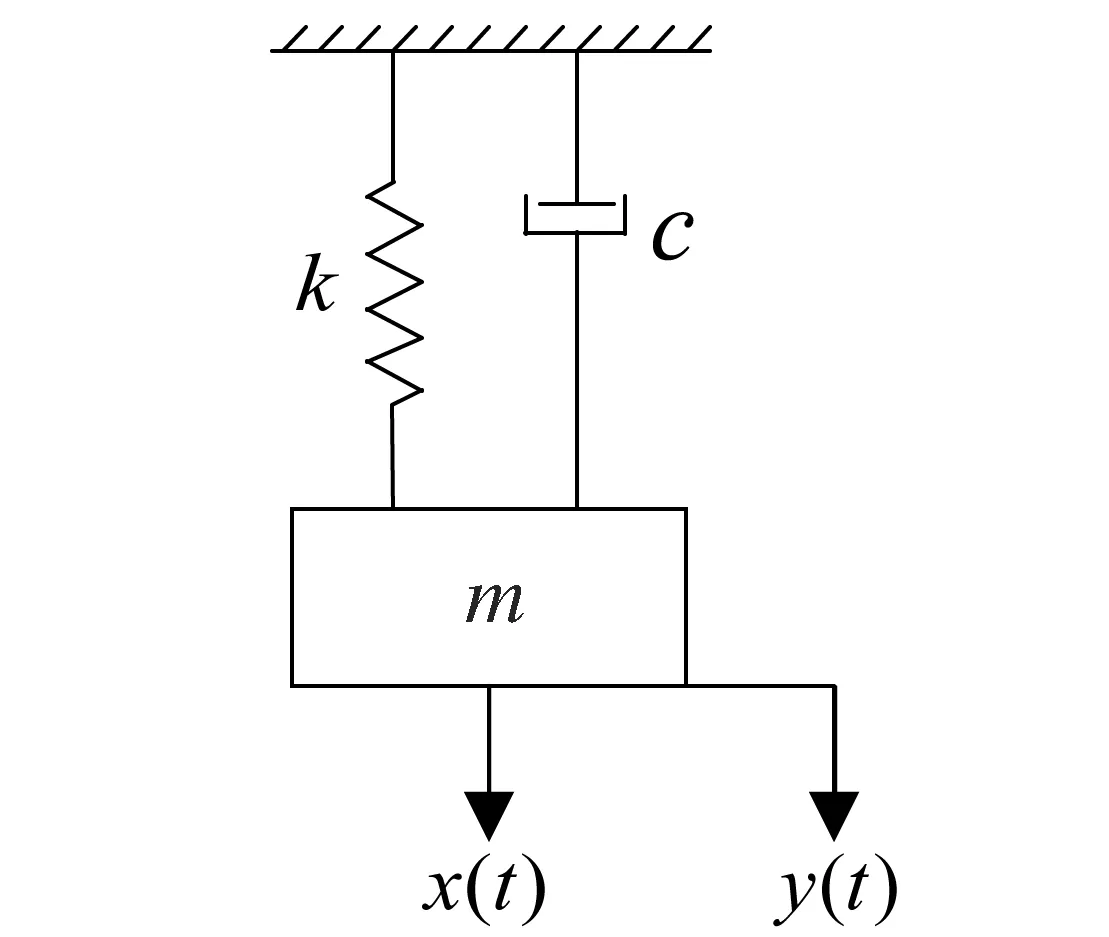
图1 二阶机械系统结构示意图

在图1中，物体受到外力的作用，其中m是物体的质量，k是弹簧的刚度系数，c是阻尼器的阻力系数，x(t)是输入系统的关于时间变化的合力，y(t)是系统输出的关于时间变化的位移，则根据牛顿第二定律得：

my″(t)+cy′(t)+ky(t)=x(t)

(1)

设输入输出函数的拉普拉斯变换为L[x(t)]=X(s),L[y(t)]=Y(s),则对于式(1)有：

m(s2Y(s)-sy(0)-y′(0))+c(sY(s)-y(0))+kY(s)=X(s)

(2)

在传递函数的推导过程中，初始条件为零，即y(0)=0,y′(0)=0,则根据传递函数的定义可以得到：

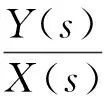
(3)

对式(3)进行代数运算可得：

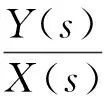
(4)

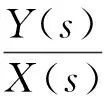
(5)

基于上述过程中对二阶系统传递函数的推导,可以看出固有频率ωn和阻尼比ξ对二阶系统的重要性，但是在相关资料中未对这两个参数进行详细的说明和解释.

2 固有频率和阻尼比的表达式证明

2.1固有频率的表达式证明

固有频率是二阶系统中一个重要的参数，是指系统在做自由振动时的振动频率，即不考虑系统的阻尼，给予系统相应的激励所产生的振动的振动频率.固有频率表达式推导条件如图2所示.

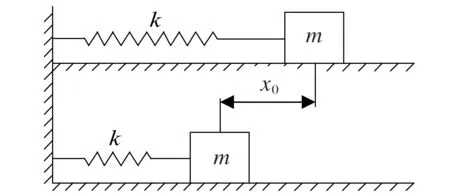
图2 固有频率表达式推导条件示意图

在图2中，开始刚度系数为k的弹簧保持原长，后经过力的作用弹簧被拉长x0的距离，此时撤去力的作用，释放弹簧，释放时为零时刻，根据牛顿第二定律得到：

mx″(t)=-kx(t)

(6)

设L[x(t)]=X(s)，则对式(6)进行拉普拉斯变换可以得到：

m(s2X(s)+sx(0)+x′(0))=-kX(s)

(7)

在零时刻，物体的位移x(0)=x0，物体的速度x′(0)=0，由此可以得到：

m(s2X(s)+sx0)=-kX(s)

(8)

对式(8)进行代数变换则有：

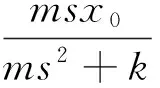
(9)

对式(9)进行反拉普拉斯变换可得：

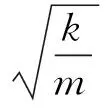
(10)

2.2阻尼比的表达式证明

阻尼是指使自由振动衰减的各种摩擦和其他阻碍作用，而阻尼比是指阻尼系数与临界阻尼系数之比，从某种意义上，阻尼比的大小决定阻尼对自由振动的衰减作用的大小.在整个阻尼比的求解过程中，临界阻尼系数的求解至关重要，而临界阻尼系数是指当阻力使振动物体刚好能不作周期性振动而又能最快地回到平衡位置的情况.根据上述定义得：

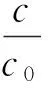
(11)

根据式(4)，为系统输入单位阶跃响应，则根据传递函数的定义可得：

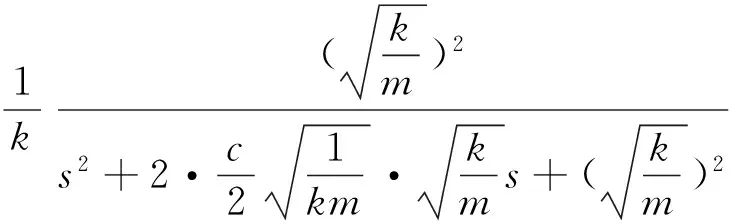
(12)

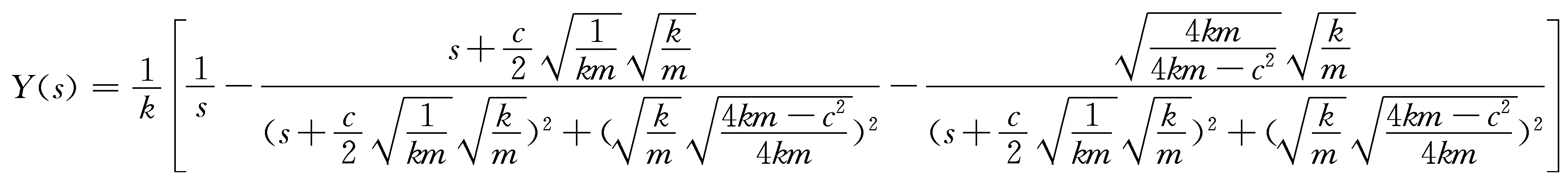
(13)

对式(13)拉普拉斯反变换可得：

(14)

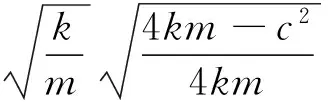
对式(14)进行求导可得：

(15)

对式(15)进行化简可得：

(16)

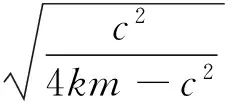
由式(16)可以看出，响应函数的导函数的正负是随着余弦函数正负的变化而变化，因此，响应函数同时存在单调递增和单调递减的区间，因此响应函数是振荡的.

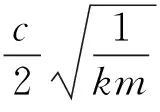
(17)

对式(17)拉普拉斯反变换可得：

(18)

对式(18)进行求导可得：

(19)

在式(19)中可以直接看出y′(t)大于零恒成立，因此输出y(t)整个响应过程中不出现振荡过程.

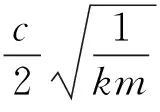
(20)

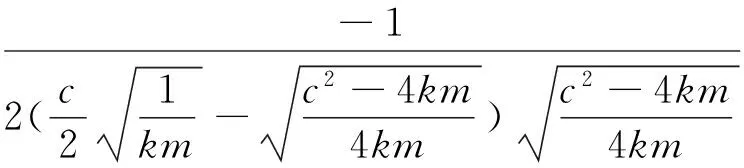
对式(20)拉普拉斯反变换可得：

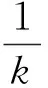
(21)

对式(21)进行求导可得：

(22)

在式(22)中可以直接看出y′(t)大于零恒成立，因此输出y(t)整个响应过程中不出现振荡过程.

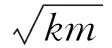
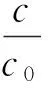
3 结语

本文旨在以拉普拉斯变换为工具直接推导出固有频率和阻尼比的表达式.整个推导过程中，紧紧围绕系统的响应函数，并根据系统的响应函数得出结论.二阶系统在日常生活中具有重要的地位，而其参数固有频率和阻尼比从根本上决定了二阶系统的性能.因此，通过对固有频率和阻尼比的表达式进行深入浅出的推导，并且以两者的实际含义为出发点，能从根本上理解这个两个参数如何对二阶系统产生影响，从而加深对二阶系统的认识.

[1]王显正，莫锦秋，王旭永．控制理论基础[M]．第2版．北京：科学出版社，2007：194-200．

[2]王华．控制工程基础[M]．北京：北京航空航天大学出版社，2011：81-91．

[3]徐泰燕．拉氏变换在自动控制理论中的应用 [J]．科技信息，2013(12)：112．

[4]刘建亚．复变函数与积分变换[M]．第2版．北京：高等教育出版社，2011：203-209．

[5]钟玉泉．复变函数论[M]．第4版．北京：高等教育出版社，2013：224-235．

TheParameterResearchofSecond-orderSystemTransferFunctionBasedonTheLaplaceTransform

JIANG Li-hui1, NIU Xin1, WANG Ran1, WANG Cheng2

(1. Department of Maths and Physics, Hefei University, Hefei Anhui 230601,China;2. Department of Mechanical Engineering, Hefei University, Hefei Anhui 230601,China)

In order to study the two order natural frequency and damping ratio in the second-order system transfer function, this paper uses the Newton’s Second Law to establish the mathematical model of differential equation and explain the two important parameters’ correctness and rationalization based on The Laplace Transform. Based on the actual meanings and related detailed proofs, the parameters of second-order system transfer function are deeply understood and better used in the actual problems.

second-order system; transfer function; inherent frequency; damping ratio ; The Laplace Transform

1673-2103(2017)05-0007-04

2017-04-06

安徽省质量工程项目(2015jyxm321,2015mooc077,2015jyxm320);国家大学生创新项目(201411059009,201511059026,201611059129);安徽省大学生创新项目(201511059018,201611059341)

江立辉(1980-),男,安徽省黄山市人,副教授,硕士,研究方向:预测与决策分析.

牛欣(1972-),女,安徽省阜阳市人,副教授,硕士,研究方向:计算数学,数值分析.

O174

A