基于多幅图像的系统三维重构的实现*

郭 元

(安徽新华学院信息工程学院，安徽 合肥 230088)

基于多幅图像的系统三维重构的实现*

郭 元

(安徽新华学院信息工程学院，安徽 合肥 230088)

以系统的图像三维重构为主要研究内容，给出基于多幅图像的三维重构数学模型.分析相机空间矩阵外方位元素求解的基本原理；分线性求解和非线性求解两种情况研究了图像三维坐标点的求解算法，并建立了相应的数学模型；通过应用某多幅灰度数字图像进行仿真验算，证明了基于多幅图像的系统三维重构方法的可行性；为相机系统识别目标在不同方位的特征信息提出了一种新的研究思路.

三维重构； 外方位元素； 相机标定； 灰度图像

相机拍摄目标物体是基于小孔成像原理[1]，其通过三维坐标变换获取空间实体的二维图像，二维图像中像素点是客观物体上点经过光线反射后投射到相机镜头的客观反映.相机可以从不同方向拍摄的同一客观实体并得到多组图像.如果对图像组进行适当处理，可以基于特定算法将二维图像的像素点反推出客观实体空间点的立体位置坐标，即：实现立体视觉三维重构.对二维图像进行三维重构，将有助于更加精准的识别目标物体的特征和参数信息[2].通过对三维物体拍摄图像序列，对图像序列进行相应的处理和变换，可以计算得到海量包含三维客观实体参数信息的特征点匹配数据集合，充分利用这些数据集合进行计算和处理，可以实现重构物体的三维坐标，尽可能还原目标物体的本来面目[3].本文在已知相机内方位元素和匹配点对的基础上，结合视觉理论推导出适用于已标定序列图像的三维重构算法.

1 基于多幅图像的三维重构数学建模

空间点X投影到第一幅图像上的点为x，点Ol为相机的光心.令矩阵P′为该幅图像的投影矩阵，P′=PT(PPT)-1是矩阵P的逆矩阵.因为点P′x满足式P+=PX，因而点P+x和点Ol都在空间点X的投影线上.如图1所示.点P′x在第二幅图像上的投影点为e，如图2所示.令e′为第二幅图像的投影矩阵，可得：

e′=P′X

(1)

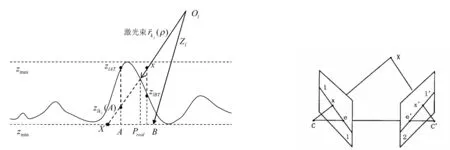
图1 单幅图像的对极几何关系 图2 多幅图像的对极几何关系

点P+x在第二幅图像上的投影在对极线l′上，由式(1)可得：

(2)

由此可得：

(3)

假设世界坐标系的中心在第一幅图像的中心，那么多幅图像的投影矩阵分别为[4]：P=K[I|0]和P′=K′[R|t]，根据投影坐标矩阵逆转原理可得：

(4)

将式(4)代入式(3)可得：

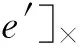
(5)

令E=[t]×R，矩阵E称为关键矩阵，与基础矩阵F的关系如下：

E=K′TFK

(6)

2 外方位元素的求解

由式E=[t]×R可知：关键矩阵与相机的外方位元素有关，经过分解可以得到旋转矩阵R和平移矩阵t.

大量的实验研究发现：关键矩阵的特征值有两个相等，另外一个为零[5][6].因而关键矩阵经过SVD分解可得：E=Udiag(1 1 0)VT.

由于ETt=0，对左式求解得：t=±U(0 0 1)T=±u3.

对于一个已知的关键矩阵E，如果第一幅图像的投影矩阵为P=K[I|0]，那么第二幅图像的投影矩阵P′有如下四种可能：

P′=[UWVT|+u3]=[UWVT|-u3]=[UWTVT|-u3]=[UWTVT|-u3]

(7)

投影矩阵的四种可能性[7～8]，如图3所示.(a)与(b)的差别是第一个相机到第二个相机的平移矢量是反向的.(a)(c)与(b)(d)的差别是基线倒置，(a)(b)与(c)(d)的差别是相机B绕基线旋转了90°.由此可以得出只有(a)是重构点同时在两个相机的前面，也就是说只需要通过验证一个空间点是否在两个相机前面就可以从4个不同的解中确定正确的投影矩阵.

图3 投影矩阵的四种可能性分析

3 三维坐标点坐标的求解

三维空间点坐标的求解算法有很多，主要分为线性求解和非线性求解两种.由于非线性求解算法计算中涉及到的参数较多，一方面可能会增加整个系统的计算量和复杂性，另一方面计算时可能会对结果产生不断的累积误差.因此本文采用线性求解的方法求出三维空间点的坐标，然后用最小二乘约束的方法对坐标点进行校正[9].该方法简单，但有可能会得到局部最优的错误结果.

假设多幅图像上的匹配点对为x和x′，可以得到基础矩阵F.结合相机的内方位元素，对基础矩阵分解可以得到多幅图像的摄影矩阵P和P′，代入投影方程，可得：

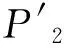
(8)

令x=PX，x′=P′X，由x×x=0，可知：x×PX=0，同理可得：x′×P′X=0.综上，可得方程组：

(9)

将式(9)化为AX=0的形式，则有：

(10)

将矩阵A进行SVD分解：A=UDVT，那么三维空间点坐标X即为矩阵V的最后一列.式(10)即为最终图像三维重构矩阵函数.

4 实验及结果

仿真实验中，首先以某已标定过的相机为模型，其内方位元素为：

实验首先对多幅图像进行重构，如图4所示.

图4 基于多幅图像的三维重构

基于多幅图像的系统三维重构算法的图像匹配结果,如图5所示.

图5 图像匹配结果

通过对图4中所列图像序列,按照式(8)～(10)进行图像匹配点三维重构，得到最终匹配点三维重构结果，如图6所示.

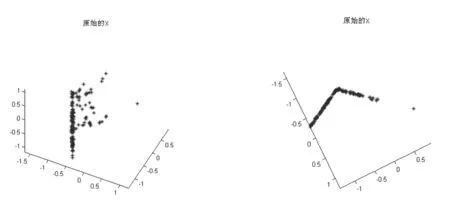
图6 图像匹配点三维重构结果

基于式(10)完成图像最终客观实体的三维重构的图像还原环节，图像重构效果如图7所示.

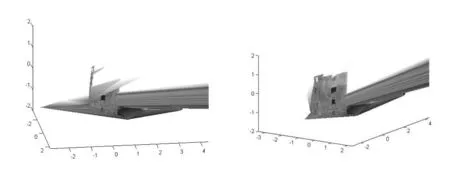
图7 客观实体三维重构结果

根据实验过程中对测试算法的精度和复杂度进行分析，统计结果见表1和表2.

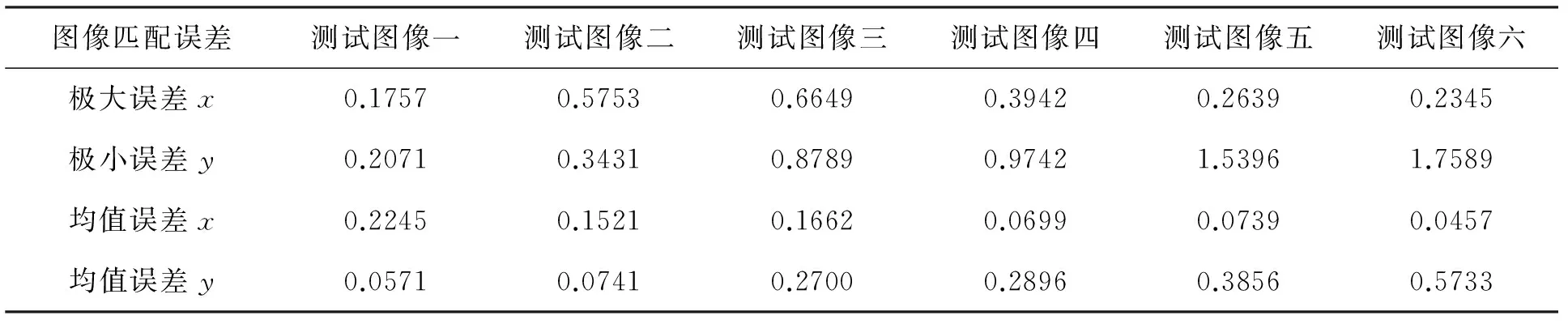
表1 实验结果图像匹配误差

表2 实验时间

表1和表2分别为稠密匹配的反投影误差分析结果及图像匹配过程所耗费时间，由于第二幅图像和第三幅图像间的视角变换比较大，导致图像匹配点数目较少，基本矩阵的精度较低，从而使图像匹配误差较大.由于采用式(10)的函数进行数值优化，第四幅测试图像和第五幅测试图像的反投影误差并没有明显的增长.因此，本文所提出的基于多幅图像的系统三维重构算法并不会出现由于中间图像误差较大而影响后续图像的三维重构.

5 结语

本文主要介绍了三维重构的基本原理，在内方为元素标定好的基础上，先对多幅图像进行重构，包括外方位元素的求取和三维坐标点的计算.得到初始的三维模型之后，通过每次添加一幅图像的方法求取剩余图像的外方位元素，并结合稠密匹配的方法得到大量的三维空间点坐标，完成整个模型的重构.之后通过实验详细介绍了序列图像的具体步骤和实验结果，通过反投影误差分析证明了课题采用的技术具有实用性.

[1]Zhang Zhengyou. Flexible Camera Calibration by Viewing a Plane from Unknown Orientations[C]//Computer Vision. The Proceedings of the Seventh IEEE International Conference on. Ieee, 1999, 1: 666-673.

[2]Zhang Zhengyou．A Flexible New Technique for Camera Calibration．IEEE. Transactions on Pattern Analysis and Machine Intelligence，2000，22(11)：1330-1334.

[3]梁志敏，高洪明，王志江．摄像机标定中亚像素级角点检测算法[J]．焊接学报，2006，27(2)：102-104.

[4]胡海峰，侯晓微.一种自动检测棋盘角点的新算法[J]．计算机工程，2004，30(14)：19-25.

[5]Lowe. D G. Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision, 2004, 60(2): 91-110.

[6]许广毅，王杨. 基于SIFT特征的单样本人脸识别研究[J].信息工程大学学报，2008，9(2)：164-167.

[7]龚志辉, 张春美,孙雷等. 改进SIFT特征描述符在影像匹配中的应用研究[J].测绘科学技术学报, 2008, 25(6): 440-447.

[8]Brown M, Lowe D G. Invariant features from interest point groups[C].//British Machine Vision Conference. Cardiff, Wales, 2002:656-665.

[9]Lowe D G. Local feature view clustering for 3D object recognition[C]. IEEE Conference on Computer Vision and Pattern Recognition,Kauai, Hawaii, 2001.

Onthe3DSystemReconstructionBasedonMultipleImages

GUO Yuan

(Institute of Information Engineering， Anhui Xinhua University， Hefei Anhui 230088，China)

This paper presents the mathematical model of 3D reconstruction based on multiple images, analyzes solution of exterior orientation element of camera matrix in both linear and nonlinear algorithms to study the three-dimensional coordinates of the image and establishes the corresponding mathematical model. Certain gray multiple digital images are used to do simulation test to prove the feasibility of 3D reconstruction method. It puts forward a new research method in the feature information in different directions for camera system.

3D reconstruction; elements of exterior orientation; camera calibration; gray image

1673-2103(2017)05-0034-05

2017-05-26

安徽省教育厅重点自然科学项目(KJ2015A300)；安徽省高等学校省级质量工程MOOC示范项目(2015mooc093)

郭元(1981-),女，安徽合肥人，讲师，硕士，研究方向：虚拟现实、智能计算.

TP391.41

A