有限长水翼在侧斜来流中激振力响应函数研究

蒲汲君，周其斗，刘文玺

（海军工程大学 舰船工程系，武汉430033）

0 引 言

水翼在湍流中的非定常升力一直以来受到许多学者的关注和研究[1]。而响应函数则是联系水翼受到的冲击脉动和环境湍流的重要方程。Sear[2]基于薄翼，无限展长和单向波数的假设得到了著名的传递函数Sear 函数。基于此理论，Liepmann[3]推导了在湍流脉动中无限长水翼的冲击响应公式，在此过程中，他忽视了湍流展长方向的变化，认为水翼的冲击响应只是简单线性湍流脉动的结果。

随后，Ribner[4]提出将简单的一维湍流波叠加以后可以得到二维湍流波模型。 在此基础上，Liepmann[5]，Diederich[6]等人研究了三维有限长水翼在同向均匀的湍流中受力问题，他们认为可以使用二维Sear 函数作为传递函数来研究有限长水翼问题，这种方法也被称为二维薄片理论。Etkin[7]发现薄片理论并不是在所有时候都同样适用，在弦长尺寸与湍流尺度相比相似或更大的情况下，二维Sear 函数不再适用。Larose 和Mann[8]，Larose[9]等人也在随后的研究中证明了此观点。

Graham[10]和Fiotas[11]考虑了三维湍流流域，在Sear 函数的基础上推导了三维传递函数，其中Fiotas[12]将计算得到的传递函数与实验结果进行了比较，发现有较大偏差。而Jackson 等人[13]运用Graham 推导的传递函数，则得到较好结果。Diederich[6]，Hakkinen[14]，zhong[15]，Massaro[16]和Li[17]进行了截面不规则时水翼的非定常升力研究。

在这篇论文中，介绍了有限长水翼的响应公式，并在此基础上推导了来流速度存在攻角和斜角下水翼的响应公式。表1 给出了本文所用到的符号及定义。

表1 符号及定义Tab.1 List of symbols and definition

1 响应函数公式推导

图1 给出了计算湍流中水翼非定常升力的数学模型。如图所示，U∞，Λ，w，C 和b 见表1 定义；x 为流向方向；y 为水翼展向方向；z 为纵向方向；k1，k2，k3为x，y，z 三个方向的波数。在推导响应函数公式时，一般将水翼假设为无厚度的薄翼，此时水翼受到的非定常升力L 是由湍流场中速度脉动引起的。这里）为下洗速度w 引起的水翼攻角变化；h）为升力L 与攻角α（t ）之间的传递函数；L 为产生的非定常升力。此时沿水翼展向方向升力分布如下式所示：

图1 数学模型Fig.1 Mathematical model

由于湍流中的速度脉动是和统计有关的变量，所以使用均方值的概念更能准确地表达该物理量。整个水翼所受到的升力均方值如下式所示：

其中：ψ （τ, y ）为攻角α（t ）关于时间t 和y 变量的自相关函数。这里引入纵向方向速度w 的自相关函数

在薄翼假设中，由于水翼表面z 方向坐标为零，所以（τ1-τ2）U∞=x1-x2且α=w/U∞，可知攻角的变化只与速度分量w 有关（速度分量：u，v，w），于是得到：

将（5）式代入（4）式中得到：

于是，将上式代入（2）式得到：

从以上推导结果可以发现，不管w 是否随z 坐标改变，φLk1（）的大小与k3无关。这为以后推导带有攻角的水翼激振力宽频谱时提供了理论基础。现在需要求得

由Graham 发现，水翼在湍流中的升力系数沿展向的分布如下所示：

其中：T （k1,k2）为传递函数，现将沿展向方向进行积分，得到这个水翼的升力系数：

水翼升力还可以表述为三维传递函数Γ （k1,k2）与下洗速度eik1xw 的乘积：

结合（12）式和（11）式可得：

三维响应函数的表达式如下所示：

当采用薄片假设时，T （k1,k2）=Se（κ），κ 为无因次频率。二维响应函数如下式所示：

这里采用Graham 计算得到的传递函数，如下式所示：

图3 给出了n=1/2 和n=1/3 时的三维响应函数以及薄片假设下的二维响应函数计算结果，将计算得到的结果分别与实验结果，Fiotas 计算结果以及Sear 函数结果进行了比较，此时的计算参数为：Λ/C=0.4，b/C=0.28。从图中分析发现，薄片假设下的二维响应函数与三维响应函数和实验结果[20]相比都相差较大，这也证明了薄片理论的局限性。而n=1/2 和n=1/3 时三维响应函数的计算结果也不相同，从图中可以看到，两条曲线的区别主要存在于介于0.1 到1 之间时，此时n=1/3 的计算结果稍稍大于n=1/2 的计算结果；在其他区域两条曲线吻合较好。与实验结果相比发现n=1/2 的计算结果与实验结果更加接近，因此在以后的分析中都采用n=1/2 的湍流波谱模型。

图2 下洗速度脉动波谱Fig.2 Spectrum of the vertical velocity fluctuations

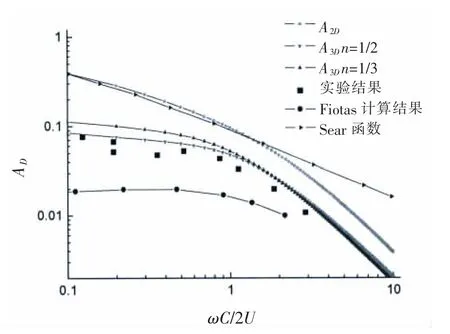
图3 响应函数计算结果Fig.3 Admittance of a finite hydrofoil

2 一定来流攻角下响应函数

从以上推导可以发现，φCL（ω ）的大小与k3无关，因此z 轴方向的参数不影响φCL（ω ）的大小，所以攻角θ 只影响来流速度Ux，对其它参数都是通过Ux来间接影响的。此时沿x 轴方向速度Ux=U∞·cosθ。所以一定攻角下的k1′和φw′（）

ω 如下式所示：

在以上定义下，升力系数的波谱函数如下式所示：

3 一定来流斜角下响应函数

在来流速度存在一定斜角下，可以使用坐标变换法研究该非定常问题，具体计算模型如图4 所示。该方法适用于C<<2b 的时候。在新的坐标系下，从相同纵坐标下的来流速度到达水翼各个点处的时间存在一定差异，这使得各个微元段的升力有一定相位差。此时，时间t′与纵坐标y 的关系式为t′=（10）式变为：

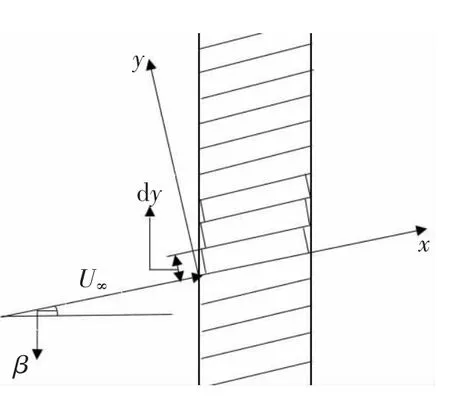
图4 计算模型Fig.4 Mathematical model

由于此时水翼展长b 远大于湍流尺度，所以k2′≈0，可以认为，将k2代入（15）式得到一定斜角下有限长水翼的响应函数为：

首先研究水翼展长b 对斜角系数的影响。设定无因次湍流尺寸Λ/C=0.4，无因次频率，变换无因次展长b/C 分别为10，15，20，计算得到的斜角系数分布如图5 所示。观察发现：随着来流侧斜角B 的增大，斜角系数随之减小，这说明时斜角越大，响应函数越小。观察还发现不同展长下的斜角系数曲线相差很小，从中可以得出结论：当水翼展长较大时，水翼展长b 几乎对斜角系数无影响。

由于无因次展长b 对斜角系数几乎无影响，以下的研究中统一设定无因次展长b/C=15。

为研究斜角B 和湍流尺度Λ 对斜角系数的影响，变化斜角B 分别取为0.1，0.3，0.5 和1，无因次湍流尺度Λ/C=0.4，计算得到的斜角系数沿无因次频率κC/2 的变化曲线如图6（a）所示。设定无因次频率κC/2=1，变换无因次湍流尺度Λ 分别为0.2，0.4，1 和3，计算得到的斜角系数沿侧斜角度B 的变化曲线如图6（b）所示。

图5 不同展长下斜角系数分布Fig.5 Skew angle coefficient distribution under different span length

图6 斜角系数变换规律Fig.6 Skew angle coefficient distribution under different factors

如图6（a）所示，随着无因次频率增大，斜角系数基本呈先增大后减小的变化趋势，各条曲线的峰值随着侧斜角B 的增大而增大，而峰值点的横坐标随着斜角B 的增大而减小。值得注意的一点是：来流存在侧斜时，会在低频的区间内使得响应函数增大，进而增大非定常升力，且来流的侧斜角越大，响应函数增大的幅度越大。但随着频率的增大，侧斜角越大，响应函数衰减得越快，也就是说非定常升力在高频区间内衰减得越快。

如图6（b）所示，在κC/2=1 下，随着侧斜角度B 增大，斜角系数呈下降趋势，该现象也能在图6（a）中得到体现。同时观察还可以发现湍流尺度越大，斜角系数越小，这说明湍流尺度的增大会加剧来流侧斜角对响应函数的影响。

4 结 论

本文进行了有限长水翼响应函数公式的推导，还研究了在来流速度存在攻角和侧斜角的情况下响应函数的变化规律，得到了以下结论：

（1）来流的攻角θ 并不影响响应函数的大小；

（2）当水翼展长较大时，展长b 对斜角系数几乎无影响；

（3）来流存在侧斜时，会在低频的区间内使得响应函数增大；在高频区间内使响应函数衰减更快；

（4）湍流尺度的增大会加剧来流侧斜角对响应函数的影响。