改进的层次分析法在钢铁企业职业危害防治综合评价指标体系权重确定中的应用*

王永斌，许春杰，张生奎，马石头，袁聚祥

改进的层次分析法在钢铁企业职业危害防治综合评价指标体系权重确定中的应用*

王永斌，许春杰，张生奎，马石头，袁聚祥#

层次分析法；指标体系；权重

目的：探讨改进的层次分析法(AHP)在指标体系权重确定中的应用，并比较其与传统层次分析法在指标体系权重确定中的效果。方法在Delphi专家咨询的基础上，基于改进的AHP法确定钢铁企业职业危害防治综合评价指标体系的权重，并与传统的AHP法相比较。结果改进的AHP法和传统的AHP法确定的一二级指标的权重均通过一致性检验，一致性指数(CI)均<0.10，且改进的AHP法的CI更小。配对t检验结果显示两种方法确定的指标体系权重比较差异无统计学意义(P均>0.05)。结论改进的AHP法确定指标体系权重的方法科学、可靠、合理，结果的准确性相对较高。

层次分析法(analytic hierarchy process，AHP)的基本原理是根据评价目的将评价对象所包含的因素进行层层分解，最终以最下层的指标衡量总评价目标[1]。目前，AHP法在统计决策领域发挥着巨大的作用。但是传统的AHP法对各级评价指标赋权的本质是根据“基数”，并非根据“序数”，这样的赋权方式难以摆脱“阿罗不可能定理”，即“阿罗困境”[2-4]。而为了摆脱根据“基数”赋权方式所产生的“阿罗困境”，作者以所在课题组在Delphi专家咨询的基础上建立的钢铁企业职业危害防治综合评价指标体系为例，确定综合评价指标体系权重时采用基于“序数”的合理赋权方式，即改进的AHP法，以探讨其在指标体系权重确定中的应用。

1 材料与方法

1.1材料建立钢铁企业职业危害防治综合评价指标体系：Delphi专家咨询法是专家会议评价法的一种发展形式，其核心是征求专家个人意见，即专家根据自己的实践经验及理论知识各自单独对评价指标进行打分，并提出自己的建议，然后将每位专家反馈的意见及打分结果进行汇总整理，将汇总整理结果再发给相应的专家，专家综合判断以后对指标再一次打分及提出建议，这样进行多次咨询→反馈→整理→再咨询→再反馈→再整理……，直至专家的意见基本趋于一致，此时所得到的方案或结论的可靠性比较大[5-7]。而整个咨询过程专家的选取是评价成败的一个主要环节[8]。该研究选取从事相关研究的高等院校老师，钢铁企业职业卫生方面的负责人和管理人员，职业病防治院、疾病预防控制中心、职业危害检测公司及相关单位的研究人员等40人，共进行3轮Delphi专家咨询，经过3轮共回收30份有效咨询问卷。根据Delphi专家咨询结果，最终确定的指标体系见表1。下文以4个一级指标为例详细说明改进的AHP法确定指标体系权重的步骤。

表1 钢铁企业职业危害防治综合评价指标体系

1.2改进的AHP法参考文献[2-4,9]。

1.2.1 对专家咨询结果进行标度 研究中第3轮Delphi专家咨询的目的就是确定指标体系的权重。根据第3轮专家对4个一级指标的打分结果，对4个一级指标的重要性进行两两比较之后，对咨询结果进行标度。标度的标准是：若咨询专家对指标Li重要性打分比指标Lj高，则在统计表格中填“+”号；若咨询专家对指标Li重要性打分与指标Lj一样，则在统计表格中填“=”号；若咨询专家对指标Li重要性打分比指标Lj低，则在统计表格中填“-”号。整个统计过程必须遵循“传递性”原则：即若咨询专家对指标Li重要性打分比指标Lj高，同时对Lj重要性打分比指标Lk高，则对Li重要性打分要比Lk高，否则打分无效，反之亦然。

1.2.2 对标度结果进行汇总整理 计算对指标Li重要性打分比Lj高的咨询专家数占总咨询专家数的百分比，记为P；对指标Li重要性打分与Lj一样的咨询专家数占总咨询专家数的百分比，记为N；对指标Li重要性打分比Lj低的咨询专家数占总咨询专家数的百分比，记为Q，则3者满足关系P+N+Q=1。

1.2.3 根据汇总的整理结果建立映射关系 映射关系建立的标准见表2。若(P-Q)的值为正值，则按表2赋值；若(P-Q)的值为负值，则对表2的赋值结果取倒数。

表2 映射关系建立的标准

1.2.4 构造判断优选矩阵 根据建立的映射关系构造4个一级指标的判断优选矩阵，矩阵形式如下。

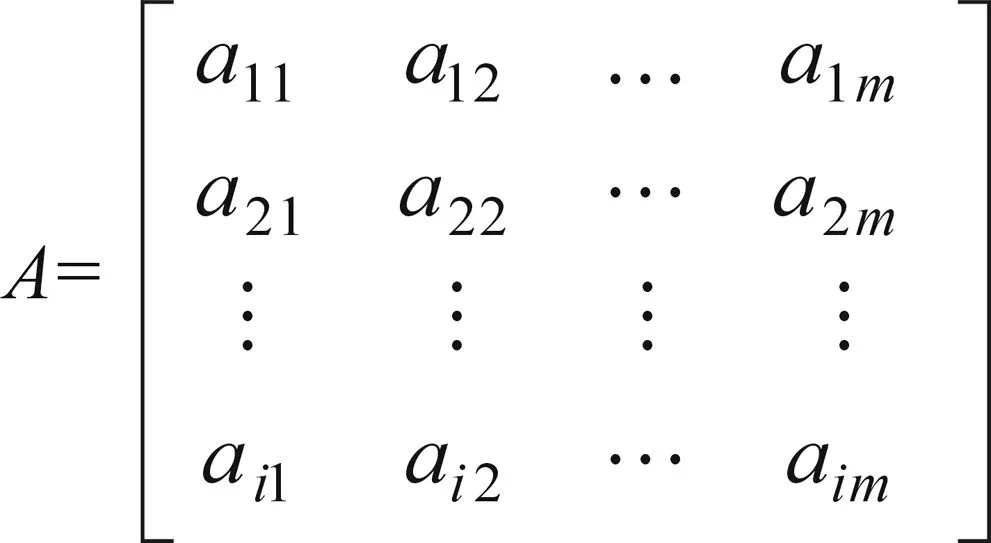
1.2.5 计算归一化权重系数 归一化权重系数的计算公式如下：

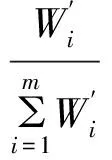
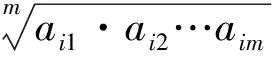
1.2.6 归一化权重系数的可接受性

应用改进的AHP法时，注意在计算归一化权重系数后，应检验所计算的权重系数是否符合逻辑，通常用一致性指数(CI)来检验多个一级指标的优先顺序有无逻辑混乱；通常认为CI<0.10时，4个一级指标的相对优先顺序可能无逻辑混乱。CI的计算公式为：

为了考察构造的判断优选矩阵的一致性是否满意，使用平均随机一致性比率(CR)对矩阵进行判断。通常，判断矩阵维数为3时，CR<0.05；判断矩阵维数为4时，CR<0.08；判断矩阵维数高于4时，CR<0.10，即认为判断矩阵具有满意的一致性。CR表达公式为：

1～9阶判断矩阵RI的取值分别为0.00、0.00、0.58、0.90、1.12、1.24、1.32、1.41和1.45。

2 结果

2.1改进的AHP结果

2.1.1 对专家咨询结果进行标度 根据第3轮Delphi专家咨询结果确定的映射关系见表3。根据表3的映射关系得到职业活动中产生的有害因素、工人自身情况、职业危害防护设施、职业卫生管理状况共4个一级指标的判断优选矩阵，见表4。根据表4计算4个一级指标的权重系数。

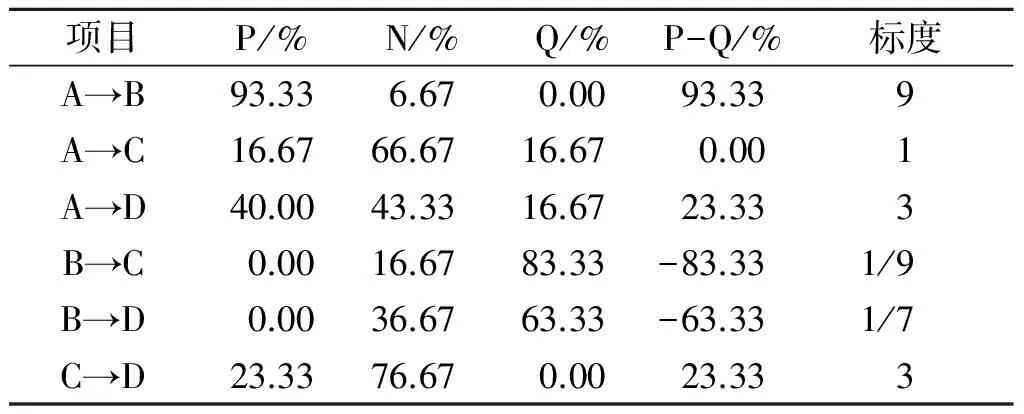
表3 基于第3轮Delphi专家咨询结果确定的映射关系

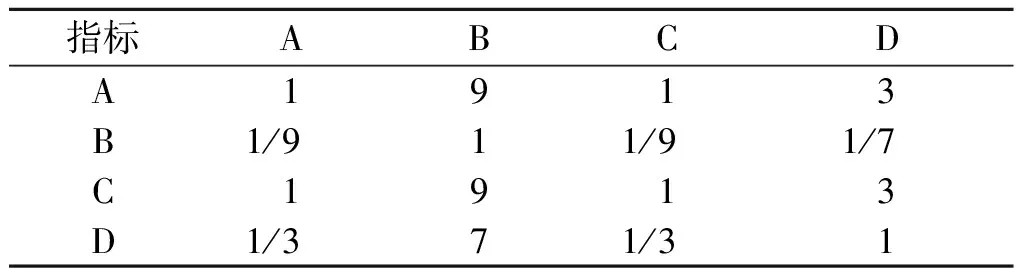
表4 根据映射关系得到的判断优选矩阵

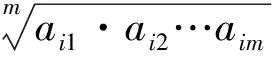
2.1.3 权重归一化处理 对职业活动中产生的有害因素，归一化权重系数为：

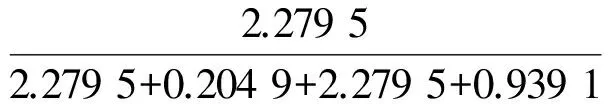
同理，对于工人自身情况、职业危害防护设施和职业卫生管理状况，评价归一化权重系数分别为：W2=0.035 9，W3=0.399 7，W4=0.164 7。

2.1.4 一致性指数 钢铁企业职业危害综合评价指标体系由4个一级指标组成(即m=4)，4个指标的归一化权重分别为0.399 7、0.035 9、0.399 7、0.164 7，4个特征向量分别为(1，9，1，3)、(1/9，1，1/9，1/7)、(1，9，1，3)、(1/3，7，1/3，1)。

λ1=(1×0.399 7+9×0.035 9+1×0.399 7+3×0.164 7)/0.399 7=4.044 5

λ2=(1/9×0.399 7+1×0.035 9+1/9×0.399 7+1/7×0.164 7)/0.035 9=4.129 5

λ3=(1×0.399 7+9×0.035 9+1×0.399 7+3×0.164 7)/0.399 7=4.044 5

λ4=(1/3×0.399 7+7×0.035 9+1/3×0.399 7+1×0.164 7)/0.164 7=4.143 7

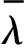
CI=(4.090 6-4)/(4-1)=0.030 2

2.1.5CR研究中第一层判断矩阵的维度为4，CR=0.030 2/0.90=0.033 6<0.08，可以认为综合评价指标体系第一层的判断矩阵具有满意的一致性。同理根据传统的AHP法[9]和以上改进的AHP法的计算步骤得到，确定的钢铁企业职业危害防治综合评价指标体系二级指标的权重及一致性见表5。可见改进的AHP法和传统的AHP法确定的一二级指标的权重均通过一致性检验(CI均<0.10)，对两种方法确定的一二级指标的权重进行配对t检验：对于一级指标t=0.815，P=0.565；对于二级指标tA=0.255，P=0.841；tB=1.346，P=0.407；tC=0.133，P=0.916；tD=1.468，P=0.381。配对t检验结果显示两种方法确定的指标体系权重之间差异无统计学意义，但通过一致性检验CI可以看出，改进的AHP法的CI均小于传统的AHP法，说明改进的AHP法更能反映出专家对指标重要性判断的一致性。改进的AHP法和传统的AHP法4个一级指标A、B、C、D的权重分别为0.399 7、0.035 9、0.399 7、0.164 7和0.358 1、0.100 2、0.359 2和0.182 5，两种方法4指标一致性检验的CI分别为0.030 2和0.047 7。

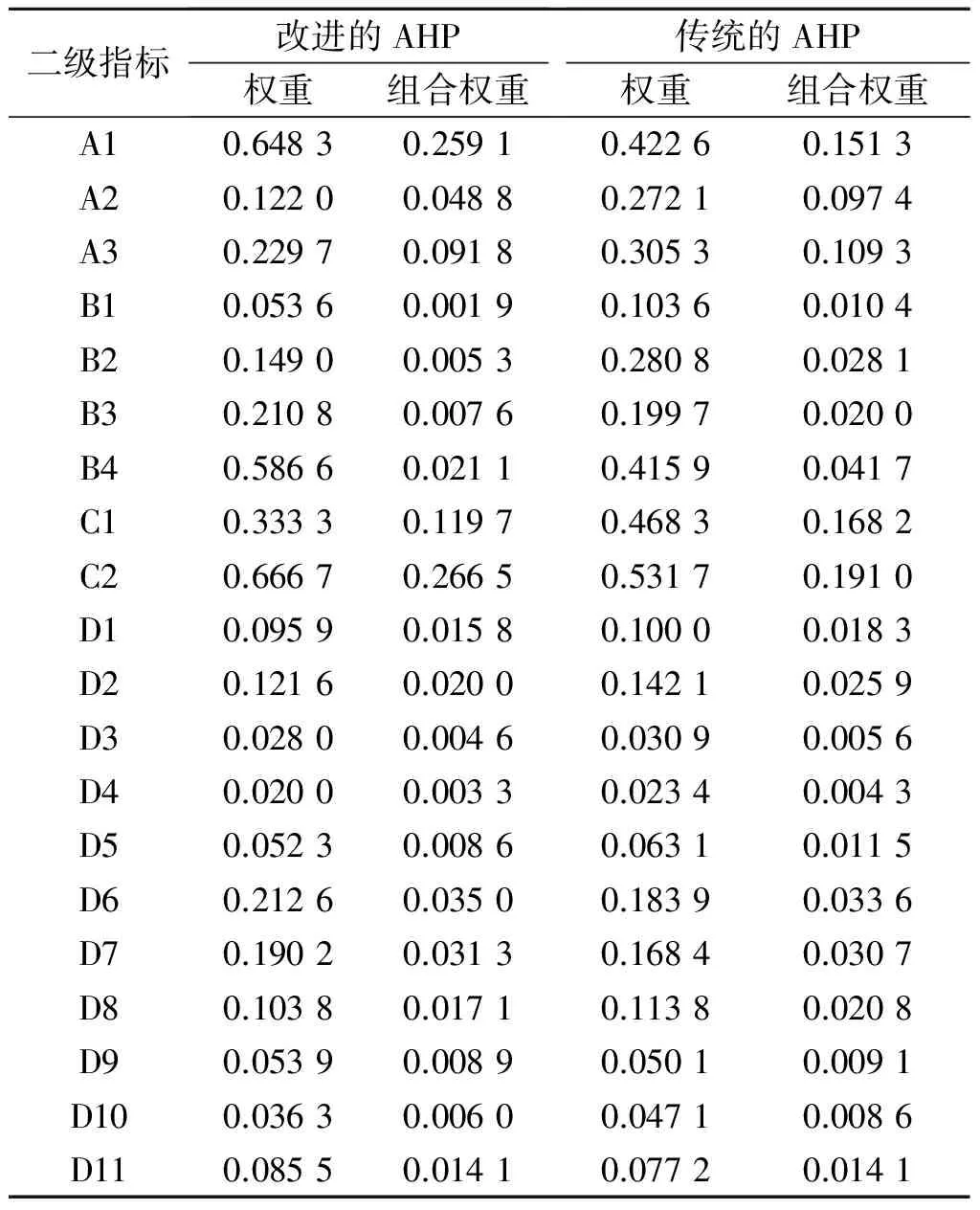
表5 两种AHP法确定的钢铁企业职业危害防治综合评价指标体系二级指标的权重及一致性

改进的AHP：A、B、C、D的二级指标的CI分别为0.001 9、0.086 6、0.000 0、0.085 4；传统的AHP：A、B、C、D的二级指标的CI分别为0.006 9、0.094 7、0.000 8、0.089 1。

3 讨论

指标体系权重的确定方法包括主观赋权法和客观赋权法。其中主观赋权法主要是专家基于自己的实践经验及理论知识，对待评价的指标进行判断而得到指标的权数，主要包括Saaty权重法、AHP法、专家评分法等，其主要缺点是容易受到赋权专家主观判断的影响，所得的结果难免存在片面性[10-11]；客观赋权法主要使用数学的方法计算指标的权重系数，如模糊定权法、相关系数法、熵权法、主成分分析法等，其主要缺点是计算得到的指标之间的权重系数，可能会与实际情况相悖[12-13]。通过查阅确定指标权重的相关文献，可发现目前确定指标权重使用最多的是AHP法，主要因为其可将定量与定性分析相结合，在某些程度上可以弱化专家主观性的影响。但是传统的AHP确定指标体系权重时主要存在以下缺陷：①问题等级之间的划分往往存在一定的模糊性。②专家根据自己的实践经历及理论知识，对问题各等级的评估往往带有一定的主观性和模糊性。③每个专家的实践经历及阅历不同，专家之间对问题等级的评估往往不尽相同且缺乏传递性原则。这样就会导致最终的赋权出现“阿罗困境”。目前根据映射关系对评价指标进行标度的方法已经在政府绩效研究中开始应用，并且研究结果也表明其可以克服传统AHP法在政府绩效评估赋权方面的困境。但这种方法在生物医学领域却鲜见报道，因此该研究以课题组建立的钢铁企业职业危害防治综合评价指标体系权重的确定为例，对传统的AHP法和改进后的AHP法确定的权重进行比较发现，尽管两种方法确定的指标体系权重之间差异无统计学意义，但改进的AHP法的CI均小于传统的AHP法。

通过对两者赋权的实质进行分析后发现，传统的AHP法在赋权过程中基于专家对指标重要性两两对比判断的“基数”，这个过程缺乏传递性原则。而改进的AHP法在赋权过程中基于专家对指标重要性的判断结果建立的映射关系，这种映射关系建立时基于“二步映射规则”，即：①所有的咨询专家独立地对指标体系的重要性进行判断。②综合所有的咨询专家对指标体系重要性的判断结果建立映射关系，再根据建立的映射关系对指标进行标度，这样的标度结果是根据所有咨询专家判断的百分比，从而摆脱个人主观性带来的影响。这个过程遵行传递性原则，操作方法也简单易行。

综上，该研究结果显示改进的AHP法在指标体系的权重确定时可以克服传统AHP法的缺陷，具有较好的应用前景。但需注意：①基于课题组建立的钢铁企业职业危害防治综合评价指标体系只有一二级指标，指标体系相对来说比较简单，改进的AHP法确定权重时准确性优于传统的AHP法。而在三级或三级以上更复杂的指标体系中，值得进一步探讨改进的AHP法确定权重的效果是否优于传统的AHP法。②改进的AHP法在确定指标体系权重时依然难以摆脱咨询专家主观性的影响。该研究只是提供一种解决思路，更好的赋权方式有待进一步研究与验证。

[1] FENG L, ZHU X, SUN X. Assessing coastal reclamation suitability based on a fuzzy-AHP comprehensive evaluation framework:a case study of Lianyungang, China[J]. Mar Pollut Bull, 2014, 89(1/2): 102

[2] SHI L,SHUAI J,XU K.Fuzzy fault tree assessment based on improved AHP for fire and explosion accidents for steel oil storage tanks[J].J Hazard Mater,2014,278:529

[3] 袁政.政府绩效评估权重设计中AHP法之改进[J].统计研究,2008,25(7):39

[4] 蔡立辉.政府绩效评估[M].北京:中国人民大学出版社,2012:97

[5] 赵镭.地税局纳税服务满意度评价指标体系的构建及应用研究[D].哈尔滨:哈尔滨工业大学,2015.

[7] 刘桂芬.医学统计学[M].2版.北京:中国协和医科大学出版社,2007:43

[8] 王芳.社区卫生服务绩效评价指标体系研究[D].武汉:华中科技大学,2006.

[9] 孙振球.医学统计学[M].3版.北京:人民卫生出版社,2010:391

[10]LAN G,TU Y.Information processing in bacteria: memory, computation, and statistical physics: a key issues review[J].Rep Prog Phys,2016,79(5):052601

[11]王晓男.综合评价中若干理论方法的适用性研究[D].长沙:湖南大学,2014.

[12]吴雪峰.基于组合赋权法的商业地产项目风险评价研究：以XJ国际商业广场为例[D].成都:成都理工大学,2014.

[13]陈伟,王忠,刘梦明,等.新疆某三级甲等综合医院临床科室医疗服务质量评价体系的建立[J].郑州大学学报(医学版),2013,48(6):795

(2016-09-20收稿 责任编辑徐春燕)

Calculating weight of comprehensive evaluation index system relative to occupational hazard prevention and control for iron and steel enterprises using modified analytic hierarchy process

WANGYongbin,XUChunjie,ZHANGShengkui,MAShitou,YUANJuxiang

SchoolofPublicHealth,NorthChinaUniversityofScienceandTechnology,Tangshan，Hebei063000

analytic hierarchy process;index system;weight

Aim: To explore the application of the improved analytic hierarchy process(AHP) in determining weight of evaluation index system and to compare with the effect of calculating the weight of the evaluation index system with the traditional AHP.MethodsThe weight of comprehensive evaluation index system of occupational hazard prevention for iron and steel enterprises was determined by improved AHP model when the Delphi being carried out, and the results were compared with those obtained by traditional AHP.ResultsThe weight of the 1ts or the 2nd level indicators calculated by the improved AHP method and the traditional AHP method were all through the consistency test with consistency index(CI)<0.10 andCIof the improved AHP was smaller than that of the traditional AHP. Pairedttest showed that there was no significant difference in the weight of the evaluation index system between the two methods(P>0.05).ConclusionThe improved AHP method used to determine the weight of the evaluation index system is scientific, reliable and reasonable, and the accuracy of the results are relatively high.

10.13705/j.issn.1671-6825.2017.06.007

*国家科技部重点研发项目 2016YFC0900605；河北省重点职业病防治技术研究项目 13277709D；河北省研究生创新项目 CXZZBS2017130； 华北理工大学研究生创新项目 2017B13

华北理工大学公共卫生学院 河北唐山 063000

#通信作者，男，1956年3月生，博士，教授，研究方向：流行病与卫生统计学，E-mail：yuanjx@ ncst.edu.cn