全国名校《解三角形》专题（A卷）

■郑州外国语学校 田 景

全国名校《解三角形》专题（A卷）

■郑州外国语学校 田 景

编者的话:强化对核心考点的演练、注重对经典题型的归纳,是学好数学的秘诀,基于此,本刊编辑部特开设此栏目,希望同学们能认真对待。从本期开始,如果都能保存好,对以后的复习大有裨益。

一、选择题(本大题共23个小题。)

1.在△ABC中,a=30,b=25,A=150°,则△ABC解的个数为( )。

A.1 B.2

C.无解 D.无法确定

2.在△ABC中,角A,B,C对应的边分别为a,b,c。若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是( )。

A.a=2b B.b=2a

C.A=2B D.B=2A

3.在△ABC中,B=60°,最大边与最小边之比为(3+1)∶2,则最大角为( )。

A.45° B.60° C.75° D.90°

4.在△ABC中,已知a2tanB=b2tanA,则△ABC的形状为( )。

A.等腰三角形 B.直角三角形

C.正三角形 D.等腰或直角三角形

5.在△ABC中,若AC·cosA=3BC·cosB,且cosC=,则A等于( )。

A.30° B.45° C.60° D.120°

6.在△ABC中,sinA∶sinB∶sinC=3∶5∶7,则△ABC是( )。

A.锐角三角形 B.直角三角形

C.钝角三角形 D.无法确定

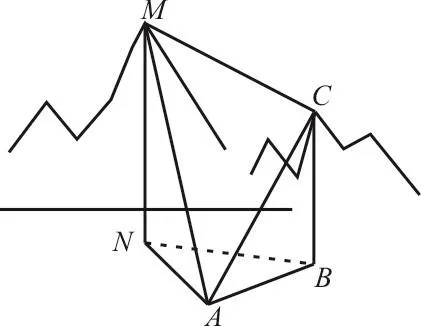
图1

7.如图1,为了测量山高MN,选择A和另一座山的山顶C为测量观测点。从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,以及∠MAC=75°;从C点测得∠MCA=60°,已知BC=100m,则MN=( )。

A.200m

B.1003m

C.150m

D.1503m

8.在△ABC中,角A,B,C的对应边分别是a,b,c,若a2-b2=3bc,sinC=23sinB,则A=( )。

A.30° B.60° C.120° D.150°

9.在△ABC中,角A,B,C的对应边分别为a,b,c,则以下结论错误的是( )。

C.若sinA＞sinB,则A＞B;反之,若A＞B,则sinA＞sinB

D.若sin3A=sin3B,则△ABC是等腰三角形

11.在△ABC中,角A,B,C的对应边分别为a,b,c,若a2=3b2+3c2-23bcsinA,则C等于( )。

A.30° B.45°

C.60° D.120°

12.在△ABC中,三条边a,b,c成等差数列,则边b对应的角B的最大值为( )。

A.30° B.45° C.60° D.120°

13.已知点O是△ABC的外接圆圆心,且AB=3,AC=4。若存在非零实数x,y,使得且x+2y=1,则cos∠BAC的值为( )。

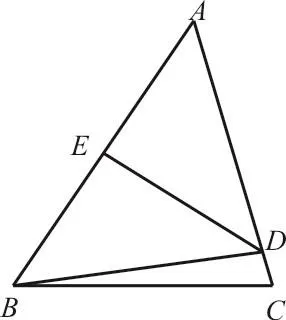
图2

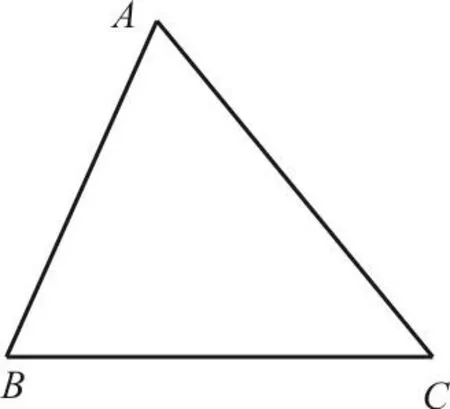
图3

15.为了竖一块广告牌,要制造三角形支架,如图3,要求∠ACB=60°,BC的长度大于1m,且AC比AB长0.5m。为了稳固好广告牌,要求AC越短越好,则AC最短为( )。

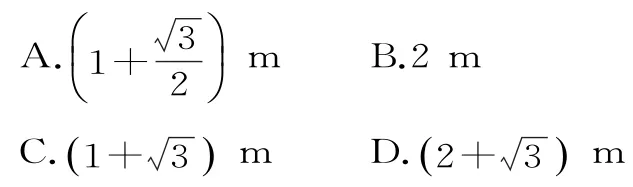
A.等边三角形 B.钝角三角形

C.直角三角形 D.等腰直角三角形

17.据气象部门预报,在距离某码头正西方向400km处的热带风暴中心正以20km/h的速度向东北方向移动,距风暴中心300km以内的地区为危险区,则该码头处于危险区内的时间为( )。

A.9h B.10h C.11h D.12h

18.在锐角△ABC中,角A,B,C的对应边分别为a,b,c,已知sin(A-B)=cosC,则的取值范围为( )。

A.(-1,1) B.(-2,2)

C.[-1,1] D.[-2,2]

19.已知a,b,c分别为△ABC的三内角A,B,C的对应边,acosC+ccosA=2bcosB,则sinA+sinC的最大值为( )。

A.2 B.3 C.1 D.2

20.在边长为2的等边△ABC的边AB、AC上分别取M、N两点,点A关于线段MN的对称点P正好落在边BC上,则AM长度的最小值为( )。

A.23-3 B.43

C.43-6 D.2

21.在△ABC中,已知a=2,则bcosC+ccosB等于( )。

A.1 B.2 C.2 D.4

22.△ABC的三边分别为a,b,c且满足b2=ac,2b=a+c,则此三角形是( )。

A.等腰三角形 B.直角三角形

C.等腰直角三角形 D.等边三角形

23.在不等边△ABC中,角A,B,C所对的边分别为a,b,c,其中a为最大边,如果sin2(B+C)＜sin2B+sin2C,则角A的取值范围为( )。

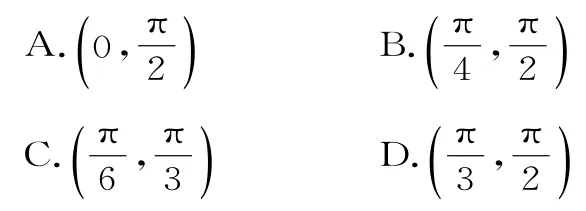
二、填空题(本大题共15个小题。)

24.在△ABC中,设角A,B,C的对应边分别是a,b,c,且C=60°,c=则

25.在△ABC中,角A,B,C的对应边分别为a,b,c,若a=sinB+cosB=2,b=2,则A的值为____。

26.在△ABC中,角A,B,C所对应的边分别为a,b,c。若a+b=,△ABC的面积为sinC,sinA+sinB=sinC,则C的值为____。

27.在△ABC中,若AB=1,AC=3,

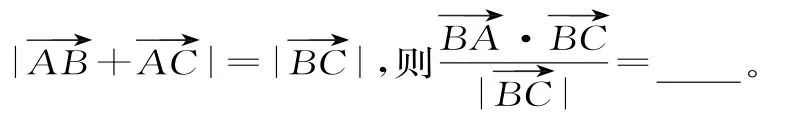
28.在△ABC中,a=x,b=2,B=45°,若该三角形有两个解,则x的取值范围是____。

29.在四边形ABCD中,A+C=180°,AB=CD=2,BC=3,AD=1,则四边形ABCD的面积等于____。

30.在△ABC中,角A,B,C所对应的边分别为a,b,c,若则△ABC的外接圆直径为____。

31.在△ABC中,AC=5,AB=12,AD为∠BAC的角平分线,D在BC上,CD=

33.在△ABC中,内角A,B,C所对应的边分别是a,b,c,有下列说法:

①若a＞b＞c,则sinA＞sinB＞sinC;

③若sin2A=sin2B,则△ABC为等腰三角形;

④若(1+tanA)(1+tanB)=2,则△ABC为钝角三角形;

⑤存在A,B,C使得tanAtanBtanC＜tanA+tanB+tanC成立。

其中正确的说法为____。(写出所有正确说法的序号)

34.设2a+2,a+1,2a-1为钝角三角形的三边,那么a的取值范围是____。

35.在△ABC中,角A,B,C的对边分别为a,b,c,已知4sin2且a+b=5,c=7,则△ABC的面积为____。

36.在△ABC中,a,b,c分别为内角A,B,C所对的边,b=c,且满足=若点O是△ABC外一点,∠AOB=θOA=2OB=2,平面四边形OACB面积的最大值是____。

37.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知c=6,sinA-sinC=sin(A-B)。若1≤a≤6,则sinC的最小值是____。

38.在△ABC中,内角A,B,C所对的边分别为a,b,c,角B≤且8sinAsinC=sin2B,则的最小值为____。

三、解答题(本大题共13个小题。)

39.已知锐角△ABC中内角A,B,C的对应边分别为a,b,c,并且a2+b2=6abcosC,sin2C=2sinA·sinB。

(1)求角C的值;

40.在△ABC中,a,b,c分别是角A,B,C所对应的边,D是BC边上靠近点B的三等分点,

(1)若2cosC(acosB+bcosA)=c,求C的大小;

(2)若c=AD=3,求△ABC的面积。

41.在△ABC中,内角A,B,C的对应边分别为a,b,c,且sin2+sinBsin

(1)求角A的大小;

(2)若b+c=2,求a的取值范围。

42.在△ABC中,角A,B,C所对应的边分别为a,b,c,已知函数f(x)=sin(2x+B)+(2x+B)为偶函数,且

(1)求b的值;

(2)若a=3,求△ABC的面积S。

图4

43.如图4,在一条海防警戒线上的点A,B,C处各有一个水声监测点,B,C两点到A的距离分别为20km和50km,某时刻B处收到发自静止目标P的一个声波信号,8s后A,C同时接收到该声波信号,已知声波在水中的传播速度是1.5km/s。

(1)设A到P的距离为xkm,用x表示B,C到P的距离,并求x的值;

(2)求P到海防警戒线AC的距离。

44.在锐角△ABC中,角A,B,C的对应边分别为a,b,c,并且2acosB=2c-b。

45.在△ABC中,角A,B,C的对应边分别为a,b,c,且

46.已知△ABC中,AC=2,A=120°,cosB=

(1)求边AB的长;

47.在△ABC中,角A,B,C的对应边分别为a,b,c,且

(1)求角C的大小;

(2)若△ABC的外接圆直径为1,求a2+b2+c2的取值范围。

48.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=24,2sinBcosC=sinA,求A,B及b,c。

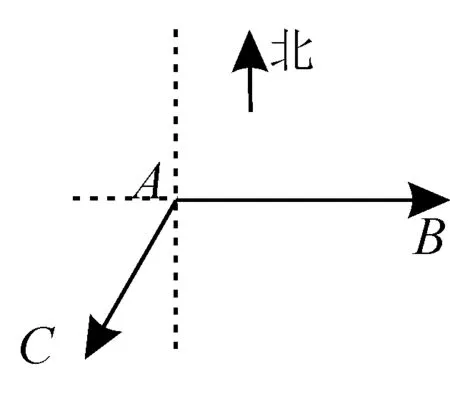
图5

49.如图5所示,当甲船位于A处时获悉在其正东方向相距20km的B处有一艘渔船遇险等待营救。甲船立即前往营救,同时把消息告知在甲船的南偏西30°方向,相距10km的C处的乙船。

(1)求处于C处的乙船和遇险渔船间的距离;

(1)求函数y=f(x)的解析式和定义域,并求出y的最大值;

(2)求函数S=g(x)的解析式和定义域,并求出S的最大值。

51.在△ABC中,a,b,c分别为内角A,B,C所对的边长,且C=,a+b=λc(其中λ＞1)。

(1)若λ=3时,证明:△ABC为直角三角形;

(责任编辑 徐利杰)