等差数列的性质及应用例析

■郑州市回民中学 芦国贤

等差数列的性质及应用例析

■郑州市回民中学 芦国贤

等差数列的知识在数列学习中占重要位置,该单元的知识点多而繁杂,同学们掌握起来比较困难。下面就等差数列的知识进行细致梳理,帮同学们形成系统的知识网络,以便牢固地掌握该知识点,为后续数列的学习打下良好的基础。

一、知识点总结

1.等差数列的基本定义。

an-an-1=d(d为常数),n≥2。

2.等差数列通项公式及推广公式。

an=a1+(n-1)d=dn+a1-d(n∈N*),首项为a1,公差为d,末项为an。

推广:an=am+(n-m)d,从而d=

3.等差中项。

(1)如果a,A,b组成等差数列,那么A叫作a与b的等差中项,即A=或2A=a+b。

(2)数列{an}是等差数列⇔2an=an-1+an+1(n≥2)⇔2an+1=an+an+2。

4.等差数列的前n项和公式。

Sn=n=An2+Bn,其中A、B是常数,所以当d≠0时,Sn是关于n的二次式且常数项为0。

二、等差数列的性质

1.当公差d≠0时,等差数列的通项公式an=a1+(n-1)d=dn+a1-d是关于n的一次函数,且斜率为公差d。

前n项和Sn=na1+是关于n的二次函数且常数项为0。

2.若公差d＞0,则{an}为递增等差数列;若公差d＜0,则{an}为递减等差数列;若公差d=0,则为常数列。

3.当m,n,p,q∈N*且m+n=p+q时,则有am+an=ap+aq,特别地,当m+n=2p时,则有am+an=2ap。一般地:a1+an=a2+an-1=a3+an-2=…。

4.若{an},{bn}为等差数列,则{λan+bn},{λ1an+λ2bn}都为等差数列。

5.若{an}是等差数列,则Sn,S2n-Sn,S3n-S2n,…,也是等差数列。

6.数列{an}为等差数列,每隔k(k∈N*)项取出一项,即am,am+k,am+2k,am+3k,…仍为等差数列。

7.设数列{an}是等差数列,d为公差,S奇是奇数项的和,S偶是偶数项的和,Sn是前n项的和。

其中an+1是项数为2n+1的等差数列的中间项。

②当项数为偶数2n时,

S奇=a1+a3+a5+…+a2n-1=

S偶=a2+a4+a6+…+a2n=

S偶-S奇=nan+1-nan=nd;

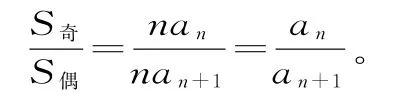
8.{an},{bn}的前n项和分别为An,Bn,且则:

9.等差数列{an}的前n项和Sn=m,前m项和Sm=n,则前m+n项和Sm+n=-(m+n)。

10.求Sn的最值。

方法一:因等差数列前n项和是关于n的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性n∈N*。

方法二:(1)当a1＞0,d＜0时,由可得Sn达到最大值时的n值。

(2)当a1＜0,d＞0时,由可得Sn达到最小值时的n值。

这样就找到了数列{an}中正负分界项。

方法三:直接利用二次函数的对称性,由于等差数列前n项和的图像是过原点的二次函数,故n取离二次函数对称轴最近的整数时,Sn取最大值(或最小值),若Sp=Sq,则其对称轴为

三、思想方法及应用技巧

1.等差数列的判定方法。

(1)定义法:an-an-1=d或an+1-an=d(常数n∈N*)⇔{an}是等差数列。

(2)等差中项:数列{an}是等差数列⇔2an=an-1+an+1(n≥2)⇔2an+1=an+an+2。

(3)数列{an}是等差数列⇔an=kn+b(其中k,b是常数)。

(4)数列{an}是等差数列⇔Sn=An2+Bn(其中A,B是常数)。

2.等差数列中的方程思想。

(1)等差数列的通项公式及前n项和公式中,涉及5个元素:a1、d、n、an及Sn,其中a1、d为基本元素。只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。

(2)设项技巧。

①一般可设通项an=a1+(n-1)d;

②奇数个数成等差数列,可设为…,a-2d,a-d,a,a+d,a+2d,…(公差为d);

③偶数个数成等差数列,可设为…,a-3d,a-d,a+d,a+3d,…(公差为2d)。

总之,解决等差数列问题时,首先,要熟练掌握基本知识点及性质,其次,要充分运用函数和方程思想,巧妙结合等差数列的性质,化繁为简,减少运算量,顺利解答。

练一练:

1.已知数列{an}中,a1=1

2.已知数列{an}中,a3=2,a7=1,数列为等差数列,求an。

3.已知公差为1的等差数列{an},Sn是它的前n项的和,若S8=4S4,求a10。

4.设数列{an}的通项为an=2n-7求的值。

5.已知等差数列{an}中,Sn是它的前n项的和,Sn=36,S2n=12,求S3n。

6.已知等差数列{an}中,前15项之和为S15=90,求a8的值。

7.已知等差数列{an},{bn}的前n项和分别为Sn,Tn,已知则求

8.已知等差数列{an}的前n项和为Sn,且S10=100,S100=10,求S110的值。

9.在等差数列{an}中,Sn为前n项和:

(1)若a1+a9+a12+a20=20,求S20;

(2)若S4=1,S8=4,求a17+a18+a19+a20的值;

(3)若已知首项a1=13,且S3=S11,问此数列前多少项的和最大。

参考答案:1.a49=2.an=3.94.153。 5.S3n=-72。6.a8=6。 78.S110=-110。 9.(1)S20=100。(2)9。(3)7。

(责任编辑 徐利杰)