赏析与数列有关的数学文化试题

■甘肃省陇南市礼县第四中学 裴雪莲

赏析与数列有关的数学文化试题

■甘肃省陇南市礼县第四中学 裴雪莲

2017年普通高中数学《考试大纲》修订内容中增加了对数学文化的要求,注重传统文化在现实中的创造性转化和创新性发展,从而实现考试的社会意义和现实目的。随着这一修订的实施,2017年各省市的高考数学模拟试题明显加大了对中华优秀传统文化内容的考核,其中数列这一章就不乏一些对数学文化的渗透和考查的试题,下面精选一些试题与同学们一起思考、赏析,感受数学文化的魅力!

一、求等差数列的前n项和

(2017年成都外国语学校高三理科模拟试题)我国古代数学著作《九章算术》有如下问题:“今有金杖,长五尺,斩本一尺,重四斤。斩末一尺,重二斤。问次一尺各重几何。”其大意是:“现有一根长五尺的金杖,一头粗,一头细。在粗的一端截下1尺重4斤。在细的一端截下1尺,重2斤。问依次每尺各重多少斤。”根据上面的已知条件,若金杖由粗到细是均匀变化的,则金杖的重量为( )。

A.12斤 B.15斤 C.15.5斤 D.18斤

解析:由题意可知等差数列中a1=4,a5=2,则所以a2=3.5,a3=3,a4=2.5。于是每一尺依次重4斤,3.5斤,3斤,2.5斤,2斤,S515,所以金杖重15斤。故选B。

点评:由题意可知等差数列的首项和第5项,再由通项公式求得公差,依次可得每尺的重量,相加可得金杖的质量;也可由等差数列的前n项和公式直接求得金杖的重量。

二、求等差数列部分项之和

(2017年长沙市高三二模试题)《九章算术》是我国古代第一部数学专著,全书收集了246个问题及解法,其中一个问题为:“现有一根九节的竹子,自上而下各节的容积成等差数列,上面四节容积之和为3升,下面三节的容积之和为4升,中间两节的容积各为多少?”则该问题中第2节,第3节,第8节竹子的容积之和为( )。

解析:设最上面一节的容积为a1,依题意可知根据等差数列的性质可知a1+a2+a3+a4=2(a2+a3)=3,解得a2+a3=

同理,a7+a8+a9=3a8=4,解得a8=所以(升),故选A。

点评:本题是求等差数列第2项、第3项及第8项的和,它不同于计算前n项和,要利用等差数列的性质巧妙求解。

三、求等差数列的项

(2017年临汾市高三二模试题)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有禀粟,大夫、不更、簪袅、上造、公士,凡五人,一十五斗,今有大夫一人后来,亦当禀五斗,仓无粟,欲以衰出之,问各几何。”

现解决如下问题:原有大夫、不更、簪袅、上造、公士5种爵位各1人,现增加一名大夫,共计6人,按照爵位共献出5斗粟,其中5种爵位的人所献“粟”成等差数列{an},其公差d满足d=-a5,请问6人中爵位为“簪袅”的人需献出粟的数量是( )。

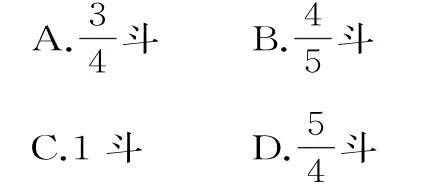
解析:由题意得:解得所以6人中爵位为“簪袅”的人需献出粟的数量是a3=a1+2d=(斗),故选A。

点评:本题考查了利用等差数列的通项公式及前n项和来求数列的第3项,利用等差数列的通项公式列出方程组,求出首项和公差,便可求得爵位为“簪袅”的人需献出粟的数量。

四、求等差数列的首项

(2017年咸阳市高三二模试题)《张丘建算经》卷上一题为“今有女善织,日益功疾,且从第二天起,每天比前一天多织相同量的布,现在一月(按30天计)共织布390尺,最后一天织布21尺”,则该女第一天共织( )尺布。

A.3 B.4 C.5 D.6

解析:由题意可设第n天织布为an,数列{an}是等差数列,公差为d,则:

所以第一天织布为5尺,选C。

点评:本题是一个等差数列问题,而首项的计算需依据题意建立方程组后求解。

五、求等差数列的项数

(2017年黄冈市高三二模理科试题)我国古代数学名著《张丘建算经》有“分钱问题”如下:“今有人与钱,初一人与三钱,次一人与四钱,次一人与五钱,以次与之,转多一钱,与讫,还数聚与均分之,人得一百钱,问人几何。”则分钱问题中的人数为

解析:设人数为n,公差为1,首项为3,则前n项和

由题意知Sn=100n,即100n,解得,n=195。故应填195。

点评:由题意,将钱分给若干人,第一人给3钱,第二人给4钱,第三人给5钱,以此类推,每人比前一人多给1钱,分完后,再把钱收回平均分给各人,结果每人分得100钱,问有多少人。即求一个等差数列的项数问题,着重考查同学们对题中文字意思的理解和关系式的建立。

六、求等差数列的公差

《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功疾,初日织五尺,今一月织九匹三丈(1匹=40尺,1丈=10尺),问日益几何。”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起每天比前一天多织相同量的布,第一天织5尺,一月织了九匹三丈,问每天增加多少尺布。”若一个月按30天算,则每天增加量为( )。

解析:由题意可得每天织布的量组成了等差数列{an},a1=5,S30=9×40+30=390。设公差为d,则30×5+390,解得故选C。

点评:根据题意不难得到每天的增加量就是等差数列的公差。根据等差数列的前n项和公式可顺利求解,但要注意单位之间的换算关系(1匹=40尺,1丈=10尺)。

七、求等比数列的公比

(2017年湘潭市高三二模理科试题)《九章算术》第三章“衰分”介绍比例分配问题:“衰分”是按比例递减分配的意思,通常称递减的比例(即百分比)为“衰分比”。今共有粮38石,按甲、乙、丙的顺序进行“衰分”,已知甲分得18石,则“衰分比”为( )。

解析:设“衰分比”为q,则18+18q+18q2=38,解得或(舍去),故选A。

点评:本题考查“衰分比”的求法,依题意知“衰分比”即为等比数列的公比,解题时要认真审题,注意等比数列性质的合理运用。

八、求等比数列的项数

(2017年赣中南五校联考)我国古代数学著作《九章算术》中有如下问题:“今有蒲生一日,长三尺,莞生一日,长一尺。蒲生日自半,莞生日自倍。问几何日而长等。”意思是:“今有蒲草第一天长高3尺,莞草第一天长高1尺。以后蒲草每天长高前一天的一半,而莞草每天长高前一天的2倍,问多少天蒲草和莞草高度相同。”根据上述已知条件,可求得第天蒲草和莞草高度相同。(已知lg2=0.3010,lg3=0.4771,结果精确到0.1)

解析:由题意可得化为解得2n=6或2n=1(舍去)。所以于是估计2.6日蒲草与莞草长度相等,故应填2.6。

点评:本题考查了利用等比数列的通项公式与求和公式计算数列的项数,考查了同学们的推理能力与计算能力。

九、求等比数列的首项

(2017年全国Ⅱ卷理科数学试题)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯。”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )。

A.1盏 B.3盏 C.5盏 D.9盏

解析:设塔的顶层共有灯x盏,则各层的灯数构成一个公比为2的等比数列,由解得x=3,故选B。

点评:“灯塔问题”也是《算法统宗》中比较著名的问题,题目以古诗的形式来描述,别具风格,依“红光点点倍加增”便知这是一个等比数列问题。

十、求等比数列的前n项和

《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何。”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半。”如果墙足够厚,Sn为前n天两只老鼠打洞长度之和,则Sn=____尺。

解析:由题意可知,大老鼠每天打洞的距离是以1为首项,2为公比的等比数列,前n天打洞之和为同理,小老鼠前n天打洞之和为

点评:根据题意可知,大老鼠和小老鼠每天打洞的距离均为等比数列,所以本题旨在考查求等比数列的前n项和公式,认真审题便可求解。

十一、求数列的通项公式

(2017年河南省新乡市二模)我国古代数学著作《九章算术》有如下问题:“今有人持金出五关,前关二而税一,次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤,问本持金几何。”其意思为“今有人持金出五关,第一关收税金第二关收税金为剩余金的第三关收税金为剩余金的,第四关收税金为剩余金的,第五关收税金为剩余金的,五关所收税金之和,恰好重1斤,问原来持金多少。”若将题中“五关所收税金之和,恰好重1斤,问原来持金多少。”改成“假设这个人原来持金为x,按此规律通过第8关,则第8关需收税金为多少”,该怎么解决呢?

解析:第一关收税金为第二关收税金为第三关收税金为可得第8关收税金为即

点评:本题考查了数列的通项公式及其应用,同学们在阅读理解文字含义的基础上需要具有一定的推理能力与计算能力,如何让项数与每关的税金建立关系是推得通项公式的关键。

十二、数列的综合问题

以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”。

该表由若干数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )

A.2017×22015B.2017×22014

C.2016×22015D.2016×22014

解析:由题意知,表中的每一行都是等差数列,且第一行公差为1,第二行公差为2,第三行公差为4,…,第2015行公差为22014,故第一行的第一个数为2×2-1,第二行的第一个数为3×20,第三行的第一个数为4×21,…,第n行的第一个数为(n+1)×2n-2,第2016行只有M,则M=(1+2016)·22014=2017×22014,故选B。

点评:本题考查了数列的通项公式及其性质,对题目提供的“表”要细致观察,认真分析,提炼其中包含的信息,从而合理利用数列知识进行解决。

通过以上数列中的数学文化试题的分析、思考与解答,我们可以感受到数列中包含了丰富的数学文化知识,而利用数列知识解决与数学文化相关的实际问题,关键是列出相关信息,合理建立数学模型——等差数列或等比数列模型;求解时要明确目标,搞清是求和、求通项、还是解递推关系问题,再根据数学推理与计算得到结果。本文主要以数列为载体讲述了数学文化的考查方向,当然还有以其他高中知识为载体的数学文化的考查,希望同学们在学习中善于归纳、整理与总结,更好地学习数学知识与数学文化!

(责任编辑 徐利杰)