理一理，等差数列的考点

■江西省瑞金市第三中学 刘小东

理一理，等差数列的考点

■江西省瑞金市第三中学 刘小东

编者的话:基本知识和基本技能是高中数学的核心,同学们一定要高度重视。愿同学们通过阅读,能从中感悟知识的结构与拓展,把握高考命题特点与趋势。

等差数列,作为最常见的一类数列,无疑在数列中有着重要的地位和应用,下面我们就来理一理等差数列的常见考点。

考点一 对等差数列基本量的考查

(1)设Sn为等差数列{an}的前n项和,若a1=1,公差d=2,Sn+2-Sn=36,则n=( )。

A.5 B.6 C.7 D.8

(2)已知等差数列{an}的前n项和为Sn,满足a13=S13=13,则a1=( )。

A.-14 B.-13

C.-12 D.-11

(3)若Sn是等差数列{an}的前n项和,且S8-S3=10,则S11的值为( )。

A.12 B.18 C.22 D.44

解析:(1)法一:由题知Sn=na1+d=n+n(n-1)=n2,Sn+2=(n+2)2,由Sn+2-Sn=36得,(n+2)2-n2=4n+4=36,所以n=8。

法二:Sn+2-Sn=an+1+an+2=2a1+(2n+1)d=2+2(2n+1)=36,解得n=8。所以选D。

(2)在等差数列{an}中,S13==13,所以a1+a13=2,则a1=2-a13=2-13=-11,故选D。

(3)数列{an}是等差数列,且S8-S3=10,故S8-S3=a4+a5+a6+a7+a8=10,5a6=10,a6=2。故S11=×11=11a6=22。故答案为C。

点评:等差数列的基本运算的解题策略:(1)等差数列的通项公式及前n项和公式共涉及五个量a1,an,d,n,Sn,知其中三个就能求另外两个,体现了用方程组解决问题的思想;(2)数列的通项公式和前n项和公式在解题中起到变量代换的作用,而a1和d是等差数列的两个基本量,用它们表示已知量和未知量是常用方法。

考点二 等差数列的判断与证明

已知数列{an}的前n项和为Sn且满足an+2Sn·Sn-1=0(n≥2),a1=。

(2)求an的表达式。

解析:(1)an=Sn-Sn-1(n≥2),又an=-2Sn·Sn-1,故Sn-1-Sn=2Sn·Sn-1,Sn≠0。

由于当n≥2时,有an=-2Sn·Sn-1=又已知a1=不适合上式。

变式1:试说明本例中数列{an}是否为等差数列。

解:当n≥2时,an+1=-,而an+1-an=-

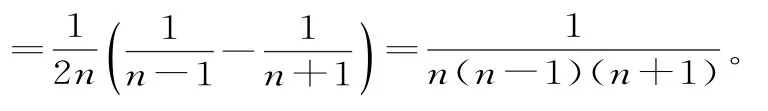
故当n≥2时,an+1-an的值不是一个与n无关的常数,故数列{an}不是等差数列。

变式2:若将本例条件改为“a1=2,Sn=问题不变,试求解。

解:(1)Sn故故

当n≥2时,an=Sn-Sn-1=

当n=1时,a1=2不适合上式。

故an=

变式3:若本例条件变为“已知数列{an}中,a1=2,an=2-(n≥2,n∈N*),设bn=(n∈N*)”,求证:数列{bn}是等差数列。

证明:an=2-故an+1=2-

故bn+1-bn=

所以{bn}是首项为b1=,公差为1的等差数列。

点评:等差数列的判定方法:(1)定义法:对于n≥2的任意自然数,验证an-an-1为同一常数;(2)等差中项法:验证2an-1=an+an-2(n≥3,n∈N*)成立;(3)通项公式法:验证an=pn+q;(4)前n项和公式法:验证Sn=An2+Bn。

注意:用定义法证明等差数列时,常采用的两个式子an+1-an=d和an-an-1=d意义不同,后者必须加上n≥2,否则n=1时,a0无定义。

考点三 对等差数列性质及应用的考查

(1)设Sn是等差数列{an}的前n项和。若a1+a3+a5=3,则S5=( )。

A.5 B.7 C.9 D.11

(2)已知数列{an}是等差数列,a1+a3+a5=105,a2+a4+a6=99,{an}的前n项和为Sn,则使得Sn达到最大的n是( )。

A.18 B.19 C.20 D.21

(3)等差数列{an}的通项公式为an=2n-8,有下列四个命题:α1:数列{an}是递增数列;α2:数列{nan}是递增数列;α3:数列是递增数列;α4:数列{a2n}是递增数列。其中真命题是

(4)一个等差数列{an}的前12项的和为354,前12项中偶数项的和S偶与前12项中奇数项的和S奇之比为则公差d=

解析:(1)由a1+a3+a5=3a3=3,得a3=1,又S5==5a3=5,故选A。

(2)a1+a3+a5=105⇒a3=35,a2+a4+a6=99⇒a4=33,则{an}的公差d=33-35=-2,a1=a3-2d=39,Sn=-n2+40n,因此当Sn取得最大值时,n=20。

(3)由已知an=2n-8可知等差数列{an}的公差d为2,故{an}是递增数列,命题α1正确;而nan=2n2-8n=2(n-2)2-8,易知数列{nan}不是递增数列,命题α2错误;易证数列是递增数列,命题α3正确有不是递增数列,命题α4错误。

综上,真命题是α1,α3。

(4)由题意,可知

又项数为12的等差数列中S偶-S奇=6d,所以d=5。

点评:在等差数列问题的解答过程中,若能灵活运用其性质,则为解题带来很大的便利,如:(1)若将性质m+n=p+q⇒am+an=ap+aq与前n项和公式结合在一起,采用整体思想,可简化解题过程;(2)等差数列奇数项和与偶数项和的性质:对于项数为偶数2n的等差数列{an},有S2n=n(a1+a2n)=…=n(an+an+1),S偶-S奇=nd对于项数为奇数(2n+1)的等差数列{an},有S2n+1=(2n+1)an+1,(其中S奇、S偶分别表示数列{an}中所有奇数项的和、所有偶数项的和)

(责任编辑 徐利杰)