高温下含多条裂纹简支钢梁的模态分析

马一江， 陈国平

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

高温下含多条裂纹简支钢梁的模态分析

马一江， 陈国平

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

基于传递矩阵方法，提出了一种在高温下对含多条裂纹简支钢梁进行模态分析的方法。在模态分析过程中，用无质量的扭转弹簧来等效横向裂纹，推导出每条裂纹产生的局部柔度；通过材料力学参数的变化引入温度模块，考虑温度变化在简支梁截面产生的轴向载荷的影响，推导出含温度参数、裂纹条数和裂纹几何参数的整条裂纹梁传递矩阵。根据简支梁的边界条件，求解出不同温度下含多条裂纹简支钢梁的固有频率。结果表明：简支梁横截面上的轴向温度载荷对固有频率的影响非常大，不能忽略不计；温度的升高会显著减小裂纹简支钢梁的各阶固有频率；随着裂纹相对深度的增大，裂纹简支钢梁第一阶固有频率和临界温度均逐渐降低。

高温；温度载荷：多裂纹；简支钢梁；固有频率

近年来，由于合金钢材料的强度较高、力学性能较好以及对环境没有污染等特点，合金钢结构在工程实际中的应用变得越来越广泛。但是，钢结构材料有一个致命的弱点就是其抗高温性能较弱，材料的力学性能对温度变化非常敏感。温度变化对结构动力学特性的影响主要有以下三种形式：①温度的变化使得结构件尺寸发生变化；②温度的变化使得结构件内部产生温度载荷；③温度的变化影响结构材料的力学特性。在高温环境下，合金钢的力学性能会发生很大程度的劣化现象，在较短的时间内就可能达到承载极限，严重危及结构件的安全性。因此，在高温下对合金钢构件进行动态特性研究具有很高的工程应用价值。

基于Euler-Bernoulli梁理论，李清禄等[1]考虑温度变化在简支梁横截面上产生轴向载荷的作用，研究了温度变化对简支梁固有频率和临界轴向力的影响。王跃兴等[2]利用有限元软件ANSYS模拟了铝合金梁在火荷载作用下的动力学响应，考察了端部约束条件和载荷比等因素对铝合金梁弯曲失效行为的影响。钱海等[3]采用二维热弹性力学理论，分析了在均匀热荷载作用下层合简支梁的振动特性，并通过有限元方法进行验证。李小年等[4]推导了简支梁固有频率关于环境温度的公式，并以一个独塔组合梁弯斜拉桥为例，采用有限元方法来量化温度对复杂结构频率的影响。于艳玲[5]利用温度传感器测量简支梁截面温度，通过动态结构测试和模态参数识别对简支梁进行分析，建立了环境温度变化与结构模态频率之间的模型。上述文献研究了环境温度变化对简支梁结构动力学特性的影响，研究表明温度的升高会不同程度地降低结构件各阶固有频率。

在工程实际应用中，在高温环境中工作的结构件很容易出现不同程度的结构损伤，并且结构损伤大多以裂纹的形式出现。而裂纹的存在会破坏结构件的强度，降低结构件工作的安全性和可靠性，因此在高温环境中对含裂纹结构件进行动力学分析受到了广大学者的关注。王振清等[6]忽略温度变化在简支梁横截面上产生的轴向温度载荷，研究了不同温度下含单条裂纹简支梁各阶固有频率的变化规律。田庆斌[7]通过有限元方法求解不同温度下含损伤简支梁桥的固有频率，并剔除温度的影响，采用BP神经网络方法识别简支梁桥的损伤参数。梁亚斌等[8]引入计算经济学的协整概念来剔除外界环境温度变化的影响，并且采用Engle-Granger两步法准确地识别出简支梁的损伤参数。上述文献探讨了温度对损伤简支梁固有频率的影响，但是忽略了简支梁横截面温度载荷的作用。对简支梁而言，温度变化时简支梁结构的长度和横截面形状并不发生变化，而是在简支梁横截面上会产生轴向温度载荷，因此温度载荷的影响不能忽略。

本文考虑梁横截面上温度载荷的影响，在高温下对含多条横向裂纹简支钢梁进行模态分析。利用无质量扭转弹簧来代替裂纹梁上每条横向裂纹，通过局部柔度的变化来表示横向裂纹对梁结构强度的破坏程度。同时将温度载荷转化为裂纹简支钢梁横截面的轴向压力，推导出整段梁含温度和裂纹参数的传递矩阵。并根据简支梁的边界条件，求解出不同温度下含多条裂纹简支钢梁的固有频率。

1 模型建立

如图1所示，本文的研究对象是一条含n条横向裂纹的简支合金钢梁，该梁为矩形等截面梁，且各向同性。该矩形截面梁的几何尺寸为：长度L、宽度b、高度h；裂纹梁上每条横向裂纹的位置为xi，且每条横向裂纹的深度为ai(i=1,2,…,n)。

图1 多裂纹简支钢梁模型

用无质量的扭转弹簧来等效每段横向裂纹，则裂纹对梁的破坏程度可以通过柔度的变化来表示。根据虚功原理，Dimarogonas等[9]推导出每条横向裂纹产生局部柔度的公式，则该裂纹梁上每条横向裂纹产生的局部柔度为：

(1)

式中：αi,T为不同温度下每条裂纹产生的局部柔度；T为温度；ET为不同温度下合金钢的弹性模量；νT为不同温度下合金钢的泊松比；I为梁横截面的转动惯量；ri=ai/h为每条裂纹的相对深度；f(ri)为每条裂纹对应的局部柔度函数，文献[9]给出了表达式如下：

(2)

由于温度的变化，简支梁的横截面受到温度载荷的作用，并且该温度载荷可以转化为横截面的轴向压力NT，李清禄等给出了温度变化在简支梁横截面产生的轴向压力表达式：

NT=ETAαsT

(3)

式中：A为裂纹梁的横截面面积；αT为在不同温度下合金钢的热膨胀系数，文献[10]给出了合金钢的热膨胀系数函数表达式：

αT=(11+0.062T)×10-6m/m·°C

(4)

式中：温度T∈[0,600 °C]。

以每条横向裂纹作为每段梁的断点，则整段裂纹梁被n条裂纹分为由n条无质量扭转弹簧连接的n+1段无损伤完整梁，且每段梁的长度为Li(i=1,2,…,n+1)。假设每段完整梁均为Euler-Bernoulli梁，则在轴向压力作用下梁的无阻尼横向振动微分方程[11]为：

(5)

式中：xi∈[0,Li]；ρT为不同温度下合金钢的密度。

根据模态分析方法，式(5)为四阶常系数线性齐次偏微分方程，可以通过分离变量法求解。假设每段完整梁具有如下形式的横向固有振动：

wi(xi,t)=Wi(xi)qi(t)

(6)

将式(6)代入式(5)，可以得到以下方程组：

(7)

(8)

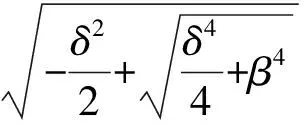
2 传递矩阵法

根据材料力学理论，Euler-Bernoulli梁横截面上的每个状态矢量(转角θ，弯矩M，剪力Q)具有如下表达形式：

(9)

(10)

通过矩阵方法将方程组(10)改写为矩阵形式：

(11)

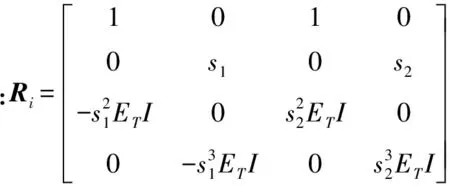
在每段梁的右端横截面的状态矢量组成的力学列阵可以表示为：

(12)

同样地通过矩阵方法，将方程组(12)改写为矩阵形式：

(13)

式中：

将式(11)代入式(13)可以得到每段梁左右两端力学列阵的传递方程：

(14)

在每条横向裂纹位置，文献[12]给出了轴向压力作用下裂纹左右表面力学列阵的传递方程：

(15)

所以，对于含n条横向裂纹的简支钢梁，右端力学列阵与左端力学列阵之间的传递关系为：

(16)

通常情况下，简支梁左右两端截面的状态矢量中挠度和弯矩为零：

(17)

因此可以从整段裂纹梁的传递矩阵中推导出一个2×2的特征矩阵HSS，则含多条横向裂纹简支钢梁固有频率的求解方程为：

detHSS=0

(18)

式(18)可以求解出该裂纹梁任意阶固有频率，而每阶固有频率对应的固有振型可以通过式(8)求解出来。

3 结果与讨论

如图(1)所示，假设该含多条横向裂纹简支钢梁的几何参数为：L=1 m，h=0.06 m，b=0.02 m；该裂纹简支钢梁的材料为低碳合金钢AISI1050[13]，常温状态下的材料参数为：E20 °C=210 GPa，ν20 °C=0.3，ρ20 °C=7 860 kg/m3。根据文献[10]，结构钢的材料密度和泊松比受到温度的影响非常小，在高温下可以用常温下的密度值和泊松比来代替，即ρT=ρ20 °C和νT=ν20 °C；而温度对结构钢弹性模量的影响非常大，因此不同温度下该低碳合金钢的弹性模量可以用以下的公式进行求解：

ET=εE20 °C

(19)

(20)

式中：ε为不同温度下结构钢弹性模量的比例系数，且温度T∈[0,600 °C]。

3.1温度变化时无裂纹简支钢梁固有频率的变化规律

假设该简支钢梁没有横向裂纹，温度的升高导致简支梁的尺寸发生膨胀，在简支梁的横截面产生轴向压力。若该简支梁的第一阶固有频率为零时(ω1,Tcr=0)，可以推导该简支钢梁的临界温度Tcr和临界压力Ncr。在不同温度下，当考虑简支钢梁横截面上的温度载荷NT=ETAαsT和忽略温度载荷NT=0时，该简支钢梁前三阶固有频率的变化规律,如图2所示。

如图2所示，考虑温度载荷与忽略温度载荷时该简支钢梁的前三阶固有频率均相差很大，所以温度变化在简支梁横截面产生的轴向压力不能忽略。考虑简支钢梁横截面的温度载荷时，随着温度的升高，该简支钢梁的前三阶固有频率均逐渐减小，且固有频率减小的速度随着温度的升高逐渐增大。由图2(a)可以得到温度升高使得简支钢梁横截面产生轴向压力，当该轴向压力随着温度升高达到临界压力Ncr=8.017 7×105N时，该简支钢梁第一阶固有频率迅速减小为零，此时简支钢梁的临界温度为Tcr=147.1 °C。

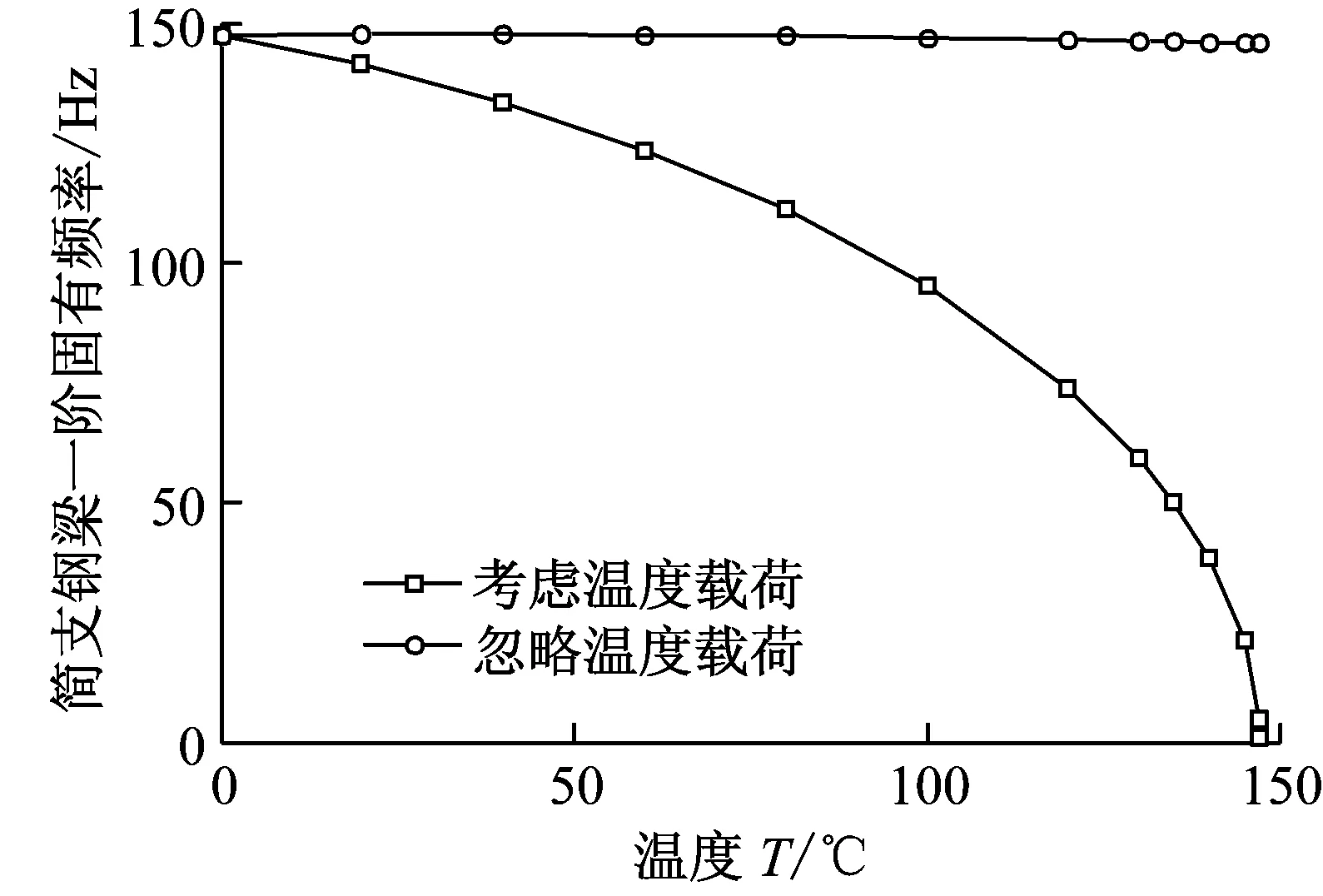
(a) 第一阶固有频率

(b) 第二阶固有频率

(c) 第三阶固有频率

Fig.2 Comparison of the first three orders natural frequencies of the simply supported steel beam in two cases

3.2含有不同条数裂纹时简支钢梁固有频率的变化规律

假设该裂纹简支钢梁存在以下三种裂纹情况：

1) 该简支钢梁仅有一条横向裂纹，且裂纹的几何参数为：x1/L=0.5，a1/h=0.1。

2) 该简支钢梁有两条横向裂纹，且裂纹的几何参数为：x1/L=0.3，a1/h=0.3；x2/L=0.5，a2/h=0.1。

3) 该简支钢梁有三条横向裂纹，且裂纹的几何参数为：x1/L=0.3，a1/h=0.3；x2/L=0.5，a2/h=0.1；x3/L=0.7，a3/h=0.3。

若每种裂纹情况的简支钢梁均处于临界温度范围内，考虑温度载荷时该简支钢梁的前三阶固有频率,如图3所示。

(a) 第一阶固有频率

(b) 第二阶固有频率

(c) 第三阶固有频率

Fig.3 First three orders natural frequencies of the simply supported beam with different number of cracks

图3所示为该裂纹简支钢梁含有不同裂纹条数时前三阶固有频率的对比图。由图3可以得到，随着温度的升高，裂纹简支钢梁的前三阶固有频率均逐渐减小，且减小的速度随着温度的升高逐渐增大。当温度不变时，随着裂纹条数的增加，裂纹对简支钢梁的破坏程度也逐渐增大，该裂纹简支钢梁的前三阶固有频率也逐渐减小；并且不论裂纹参数如何，固有频率减小的速度随着温度的升高逐渐增大。由图3(a)可以得到，随着裂纹条数的增加，该裂纹简支钢梁的临界温度也逐渐降低。

3.3裂纹位置不同时简支钢梁固有频率的变化规律

假设该裂纹简支钢梁仅有一条横向裂纹，且该裂纹的相对位置和相对深度分别为为：x1/L∈[0,1]，a1/h=0.3。若温度参数为T=0 °C,50 °C,100 °C保持不变，该裂纹简支钢梁的前三阶固有频率如图4所示。

(a) 第一阶固有频率

(b) 第二阶固有频率

(c) 第三阶固有频率

由图4可以得到，从图形上来看，该裂纹简支钢梁的前三阶固有频率变化曲线关于简支梁中点位置的横截面是左右对称的。当裂纹处于简支钢梁的中点时，该裂纹对简支钢梁的破坏程度最大，同时该裂纹简支钢梁的第一阶固有频率最小；该裂纹简支钢梁的第二阶模态存在一个节点，并且节点位于简支梁中点位置；该裂纹简支钢梁的第三阶模态存在两个节点，且节点位置如图4(c)所示。随着温度地逐渐升高，该裂纹简支钢梁的前三阶固有频率均逐渐减小。

3.4裂纹条数对简支钢梁固有频率的影响

假设该裂纹简支钢梁存在以下四种裂纹情况：

1) 该简支钢梁不含横向裂纹。

2) 该简支钢梁仅有一条横向裂纹，且裂纹的几何参数为：x1/L=0.5，a1/h=0.3。

3) 该简支钢梁有两条横向裂纹，且裂纹的几何参数为：x1/L=0.3，a1/h=0.3；x2/L=0.5，a2/h=0.3。

4) 该简支钢梁有三条横向裂纹，且裂纹的几何参数为：x1/L=0.3，a1/h=0.3；x2/L=0.5，a2/h=0.3；x3/L=0.7，a3/h=0.3。

若温度T=100 °C保持不变，则四种不同裂纹情况下该简支钢梁前三阶固有频率如表1所示。

表1裂纹条数不同时简支钢梁前三阶固有频率

Tab.1Firstordernaturalfrequenciesofthesimplysupportedsteelbeamwithdifferentnumbersofcracks

Hz

如表1所示，当每条裂纹均不在各阶模态节点位置时，随着裂纹条数的增加，裂纹简支钢梁的前三阶固有频率逐渐减小。若简支钢梁仅有一条裂纹且该裂纹处于第二阶模态节点，裂纹的存在对裂纹简支钢梁第二阶固有频率影响不大。

3.5温度和裂纹深度不同时简支钢梁固有频率的变化规律

假设该裂纹简支钢梁仅有一条横向裂纹，且该裂纹的几何参数为：x1/L=0.5、a1/h∈[0,0.5]。若温度T∈[0,100 °C]，则温度和裂纹深度不同时对应的裂纹简支钢梁前三阶固有频率变化规律,如图5所示。

图5所示为当裂纹相对位置不变时，不同裂纹相对深度和温度下裂纹简支钢梁前三阶固有频率的变化规律。随着温度的降低，该裂纹简支钢梁的各阶固有频率均逐渐减小，并且减小的速度逐渐增大。随着裂纹相对深度的增大，该裂纹简支钢梁的第一、三阶固有频率逐渐减小；由于裂纹位于简支钢梁的第二阶模态节点上，因此，随着裂纹相对深度的增大，该裂纹简支钢梁的第二阶固有频率基本保持不变。

(a) 第一阶固有频率

(b) 第二阶固有频率

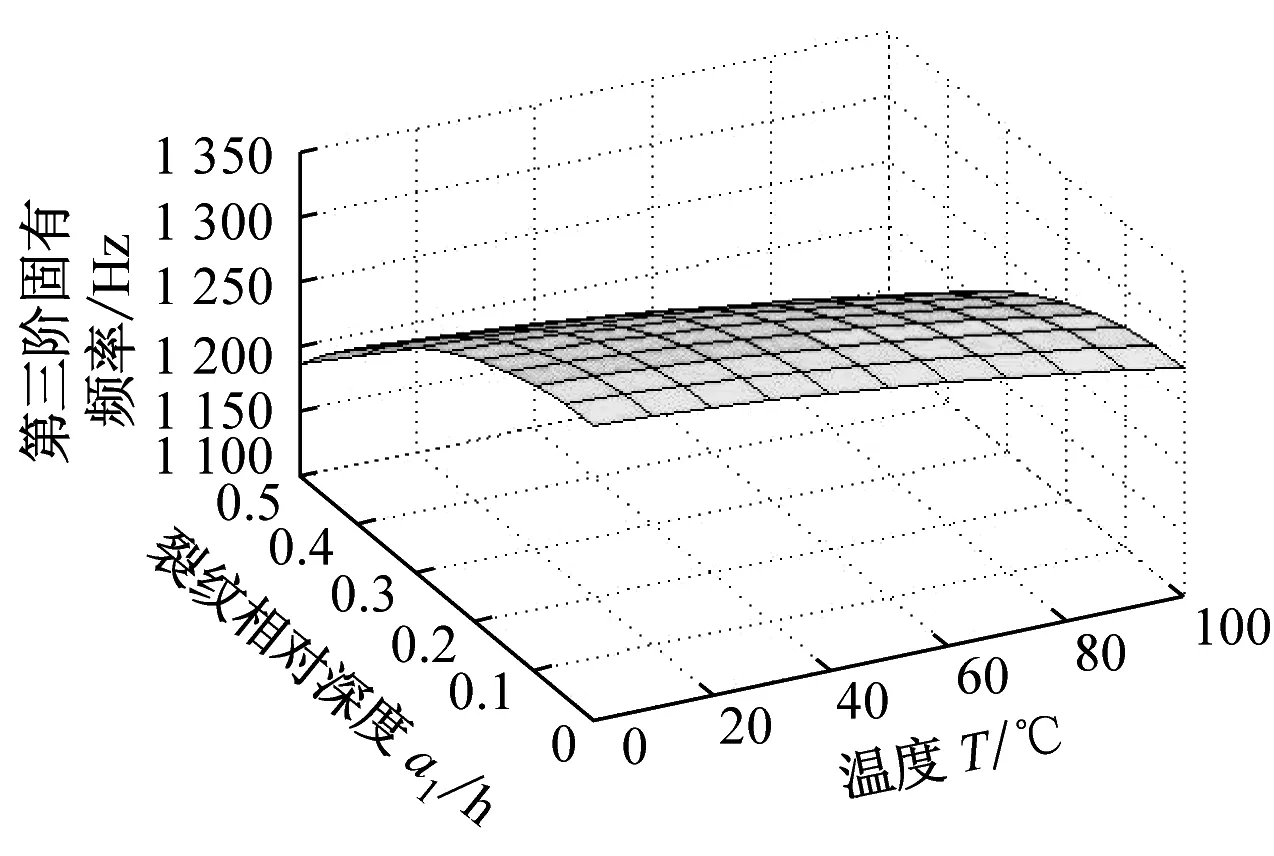
(c) 第三阶固有频率

3.6裂纹深度和位置不同时简支钢梁固有频率的变化规律

假设该裂纹简支钢梁仅有一条横向裂纹，且该裂纹的相对位置和相对深度为：x1/L∈[0,1]，a1/h∈[0,0.5]。若温度T=0 °C保持不变，则裂纹相对位置和相对深度不同时该裂纹简支钢梁前三阶固有频率的变化规律,如图6所示。

(a) 第一阶固有频率

(b) 第二阶固有频率

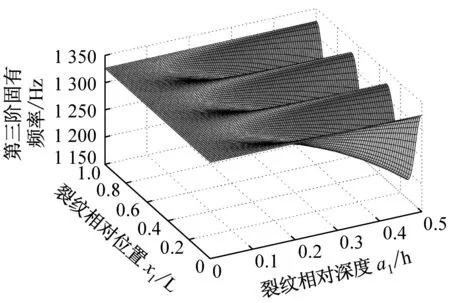
(c) 第三阶固有频率

图6所示为裂纹的相对位置和相对深度不同时该简支钢梁前三阶固有频率的变化规律。随着裂纹相对深度的增大，该裂纹简支钢梁的前三阶固有频率逐渐减小；仅当裂纹位置处于简支钢梁的各阶模态的节点时，该裂纹简支钢梁相对应阶固有频率受裂纹相对深度的影响不是很大。简支钢梁的第二阶模态有且仅有一个节点，位于简支梁中点位置；简支钢梁的第三阶模态有两个节点，从图4(c)可以看出。

3.7裂纹深度不同时简支钢梁临界温度的变化规律

假设该裂纹简支钢梁存在以下三种裂纹情况：

1) 该简支钢梁仅有一条横向裂纹，且裂纹的几何参数为：x1/L=0.5，a1/h∈[0,0.5]。

2) 该简支钢梁有两条横向裂纹，且裂纹的几何参数为：x2/L=0.3，a2/h=0.3；x1/L=0.5，a1/h∈[0,0.5]。

3) 该简支钢梁有三条横向裂纹，且裂纹的几何参数为：x2/L=0.3，a2/h=0.3；x1/L=0.5，a1/h∈[0,0.5]；x3/L=0.7，a3/h=0.3。

则三种不同裂纹情况下该裂纹简支钢梁临界温度的变化规律,如图7所示。

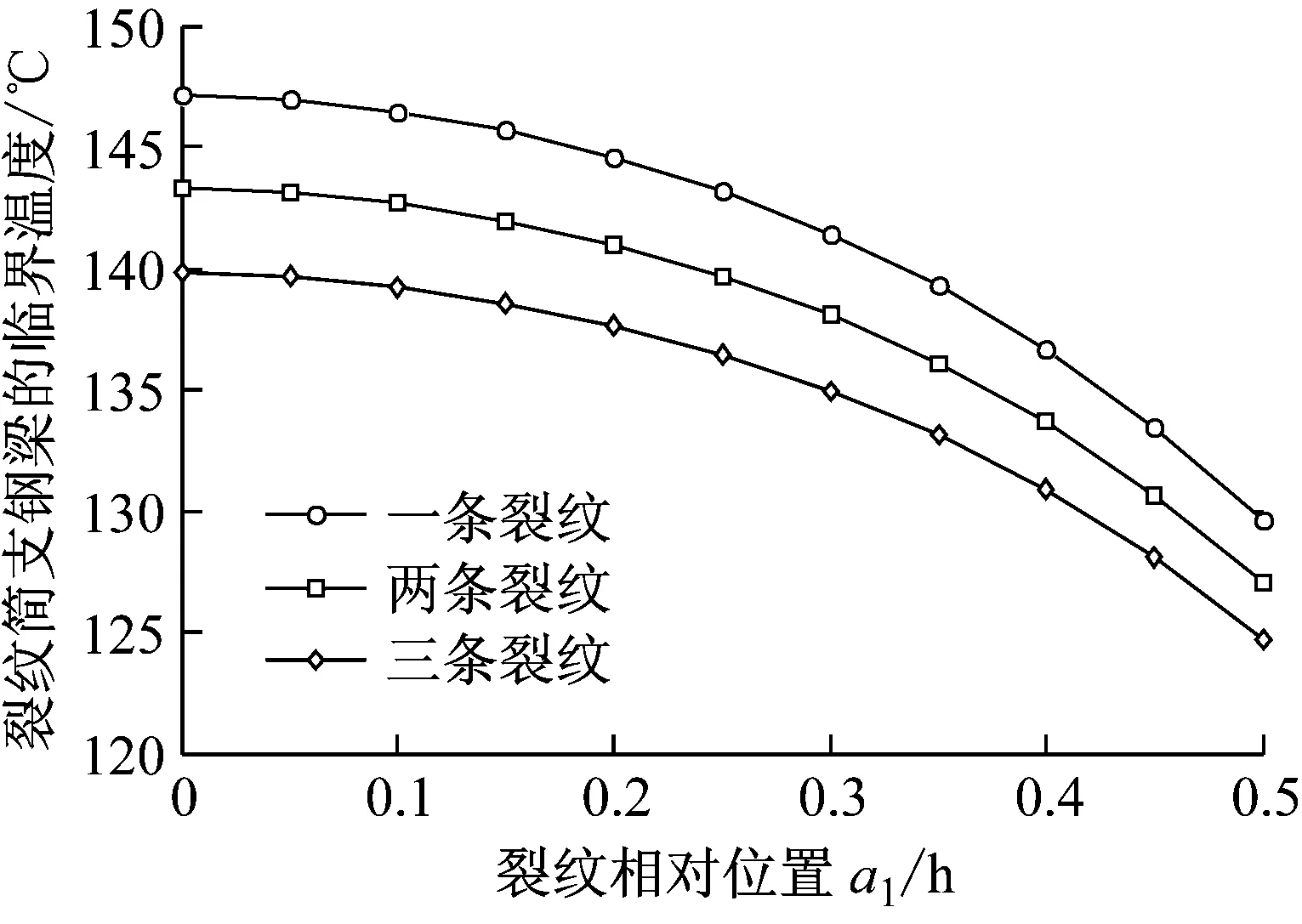
图7 不同裂纹参数对应的简支钢梁临界温度

Fig.7 Critical temperatures of the simply supported steel beam with different parameters of cracks

图7所示为裂纹条数和相对深度不同时该裂纹简支钢梁临界温度的变化规律。随着第一条裂纹相对深度的增大，该裂纹简支钢梁的临界温度逐渐降低，并且降低的速度逐渐增大。随着裂纹条数的逐渐增加(裂纹对简支钢梁的破坏程度逐渐增大)，该简支钢梁的临界温度也逐渐降低。

4 结 论

温度的升高引起简支梁结构出现热膨胀现象，在简支梁的横截面产生轴向压力。在含多条裂纹简支钢梁的模态分析过程中，考虑到温度变化对材料力学特性以及简支梁横截面载荷的影响，利用扭转弹簧来代替横向裂纹，并通过传递矩阵方法分析温度变化对含多条裂纹简支钢梁模态的影响。主要得到以下结论：

(1) 温度变化在简支梁横截面产生的轴向压力对简支钢梁模态的影响非常大，不能忽略。随着温度的升高，简支钢梁的各阶固有频率均逐渐减小。

(2) 若裂纹不处于简支钢梁各阶模态节点位置，随着裂纹相对深度的逐渐增大(裂纹对简支钢梁破坏程度的增大)，简支钢梁的各阶固有频率均逐渐较小。

(3) 当裂纹简支钢梁仅有一条横向裂纹时，该裂纹简支钢梁的各阶固有频率随着裂纹相对位置的变化关于简支钢梁中点横截面是左右对称的。

(4) 随着裂纹相对深度的增大，裂纹简支钢梁的临界温度也逐渐降低，并且降低的速度逐渐增大。

[1] 李清禄, 陈伟年. 面内温度载荷作用下简支梁的振动和稳定[J]. 甘肃联合大学学报(自然科学版), 2007, 21(3):36-37.

LI Qinglu, CHEN Weinian. Vibration and stability of simply supported beam subjected to temperature load[J]. Journal of Gansu Lianhe University(Natural Science Edition), 2007, 21(3):36-37.

[2] 王跃兴, 谭英华, 席丰. 受火作用铝合金梁的临界温度及其参数分析[J]. 应用力学学报, 2014, 31(1):73-79.

WANG Yuexing, TAN Yinghua, XI Feng. Critical temperature and parameters analysis of the aluminum alloy beam subjected to fire load[J]. Chinese Journal of Applied Mechanics, 2014, 31(1):73-79.

[3] 钱海, 周叮, 刘伟庆,等. 均匀热荷载作用下层合简支梁的弹性力学解[J]. 力学季刊, 2013, 34(2):331-336.

QIAN Hai, ZHOU Ding, LIU Weiqing, et al. Elasticity solution of simply supported laminated beams subjected to uniform thermo-load[J]. Chinese Quarterly of Mechanics, 2013, 34(2):331-336.

[4] 李小年, 陈艾荣, 马如进. 温度对桥梁模态参数的影响[J]. 华南理工大学学报(自然科学版), 2012, 40(4):138-143.

LI Xiaonian, CHEN Airong, MA Rujin. Influence of temperature on modal parameters of bridge[J]. Journal of South China University of Technology(Natural Science Edition), 2012, 40(4):138-143.

[5] 于艳玲. 温度对结构模态频率影响研究[D]. 大连:大连交通大学, 2010.

[6] 王振清, 刘兵, 韩玉来. 高温下含裂纹铝合金梁自由振动频率分析[J]. 哈尔滨工程大学学报, 2012, 33(3):320-324.

WANG Zhenqing, LIU Bing, HAN Yulai. Free vibration frequency variation analysis of a cracked aluminum alloy beam under temperatures[J]. Journal of Harbin Engineering University, 2012, 33(3):320-324.

[7] 田庆斌. 考虑温度效应的简支梁桥损伤识别方法研究[J]. 北方交通, 2014(8):4-6.

TIAN Qingbin. Damage identification for simply-supported bridge considering temperature effect[J]. Northern Communications, 2014(8):4-6.

[8] 梁亚斌, 李东升, 李宏男. 环境温度影响下基于频率协整的在线损伤识别[J]. 大连理工大学学报, 2014(3):307-314.

LIANG Yabin, LI Dongsheng, LI Hongnan. Online damage detection based on cointegration of frequencies under influence of environmental temperature[J]. Journal of Dalian University of Technology, 2014(3):307-314.

[9] DIMAROGONAS A D, PAIPETIS S A, CHONDROS T G. Analytical methods in rotor dynamics[M]. Springer, Mechanisms & Machine Science, 1983, 9.

[10] 李国强，蒋首超，林桂祥。钢结构抗火计算与设计[M].北京：中国建筑工业出版社，1999：75-98.

[11] MEIROVITCH L. Elements of vibration analysis[M]. McGraw-Hill international editions, 1986.

[12] BINICI B. Vibration of beams with multiple open cracks subjected to axial force[J]. Journal of Sound and Vibration, 2005, 287(1): 277-295.

[13] DENTSORAS A J, DIMAROGONAS A D. Resonance controlled fatigue crack propagation in a beam under longitudinal vibrations[J]. International Journal of Fracture, 1983, 23(1): 15-22.

Modalanalysisofasimplysupportedsteelbeamwithmutiplecracksunderhightemperature

MAYijiang,CHENGuoping

(The State Key Laboratory of Mechanics and Control for Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Based on the transfer matrix method, an analytical method was proposed to conduct the modal analysis of a simply supported beam with multiple cracks under high temperature. In the modal analysis, transverse cracks were replaced by torsional springs without mass, and the local flexibility of each crack was derived. The temperature module was introduced by the change of the mechanical parameters of the structural material. Considering the axial load of the simply supported beam caused by the variation of temperature, the transfer matrix of the whole cracked beam including the temperature parameter and the number and geometric parameters of cracks was obtained. According to the boundary conditions, the natural frequencies of the simply supported steel beam with multiple cracks were calculated. The results indicate that the influence of the axial temperature load on the natural frequencies of the simply supported steel beam is rather great, and can not be ignored. The increase of the temperature can significantly decrease each order of natural frequencies of the cracked simply supported steel beam. The first order natural frequency and critical temperature of the cracked simply supported steel beam gradually decrease as the relative depth of cracks increases.

high temperature; temperature load; multiple cracks; simply supported steel beam; natural frequency

V224

A

10.13465/j.cnki.jvs.2017.21.009

江苏高校优势学科建设工程基金(PAPD)

2016-05-03 修改稿收到日期：2016-08-18

马一江 男，博士，1989年8月生

陈国平 男，博士，教授，博士生导师,1956年生。Email：gpchen@nuaa.edu.cn