基于滑移信息熵与最优滤波器构建的故障诊断方法

童水光， 徐 剑， 从飞云， 唐 宁， 张依东

(1.浙江大学 机械设计与自动化研究所，杭州 310027； 2.浙江大学 热工与动力系统研究所，杭州 310027)

基于滑移信息熵与最优滤波器构建的故障诊断方法

童水光1， 徐 剑2， 从飞云1， 唐 宁2， 张依东1

(1.浙江大学 机械设计与自动化研究所，杭州 310027； 2.浙江大学 热工与动力系统研究所，杭州 310027)

以故障信号局部包含信息的差异性为基础，结合相空间重构和信息熵理论，提出滑移信息熵序列对故障信息进行局部冲击特征识别。在此基础上，引入最小熵反卷积、最优滤波器构建等理论，成功实现了滚动轴承的微弱故障诊断。仿真数据和实验数据分析论证结果表明，提出的故障特征提取技术对于滚动轴承微弱冲击故障特征具有优越的识别和提取能力，对于实现滚动轴承强噪声背景下故障智能诊断具有重要的意义。

信息熵；滑移截取；最优滤波器；特征提取；滚动轴承

机械故障诊断是一门理论研究与工程应用紧密结合的学科，它以故障机理和检测技术为基础，以信号处理和模式识别为基本方法，并随着计算机和通信技术的发展而迅速发展。随着现代工业的快速发展，机械设备系统集成度不断提高，结构日趋复杂，单一部件发生故障若不进行及时处理，往往会引起整个系统的崩溃，甚至导致不可预知的灾难性后果。因此，对机械系统实行状态监测和故障诊断对设备安全高效运行有着重大意义。近几年，随着现代信号处理技术的发展，各种故障诊断方法不断涌现，如自适应滤波技术、谱峭度分析技术、奇异值分解技术、多源信息融合技术等，大大丰富了故障特征提取手段[1-3]。

熵是系统状态函数，用来表示能量在空间中分布的均匀程度。1948年Shannon采用概率论和统计学方法，把熵的思想引入到信息论中，首次解决了对信息的量化度量问题。在此基础上，Pincus和Richman[4-5]分别提出了近似熵和样本熵的概念，为信息熵理论的进一步发展应用打下了基础。现今，信息熵理论在旋转机械故障诊断领域中有了广泛的应用。杨文献等[6]基于信号奇异值分解技术，提出了奇异熵的概念，实验表明该指标在机械信号信息量评估、信息成分分析以及信号降噪等方面性能优越；张雨等[7]在时间序列符号化的基础上, 建立符号树信息熵指标，成功实现内燃机振动信号瞬态特征的提取；Yang等[8]提出了基于经验模态分解的能量熵概念，并结合神经网络实现对滚动轴承故障精确分类；夏勇等[9]在研究相空间重构理论的基础上，首次提出了关联距离熵的概念，揭示了系统的本质特征，在柴油机故障诊断中取得了较好的效果；Yu等[10]在信号时频分析的基础上提出了时频熵的概念，实验证明其能准确识别齿轮故障特征；郑近德等[11]提出用多尺度模糊熵度量时间序列的复杂度，并结合支持向量机实现滚动轴承故障诊断。

以上采用信息熵的故障特征提取方法中，往往对信号整体进行信息熵计算，缺少对信号局部特征信息的提取；此外，对于一维振动信号序列，数据值的范围并不确定，按理论公式进行信息熵计算存在困难。根据上述的研究现状和不足，本文提出一种基于滑移信息熵与最优滤波器构建的故障诊断方法。它采用对时间序列滑移截取的思路，通过相空间重构，得到一个信息熵序列，再结合重构冲击成分的时频分析，构建最优滤波器，从而实现对故障冲击的识别提取，并能够实现滚动轴承微弱故障的有效诊断。

1 滑移信息熵故障诊断方法

1.1振动信号时域的信息熵特征

当旋转机械出现故障缺陷时，往往会伴随着周期性的冲击成分信号。分析表明该类故障信号可以近似认为由冲击主导区域和非冲击主导区域两部分组成[2]。如何利用信号处理手段区分该两部分信号是本文的研究重点。

信息熵是信息论中信息无序度的度量, 信息熵越大, 信息的无序度越高，信息的效用值越小；反之，信息熵越小，信息的无序度越小，信息的效用值就越大。因此，信息熵可用于评估系统中所含信息效用值的大小。如果一个离散序列X={x1，x2,…xn}，p(xj)表示系统中某一事件xj发生的概率，其信息熵H的计算公式如下：

(1)

对于包含冲击奇异信号的振动信号，在冲击主导区域，由于冲击信号主要有冲击衰减振荡组成，信号组成成分相对简单，用信息熵H来衡量，该处的H值较低；相反，在非冲击主导区域，信号主要由噪声信号组成，信号随机性强、成分复杂，故H值较高。根据这个规律，我们可以对振动信号进行分断截取，通过分析每段信号的信息熵来达到信号奇异性提取的目的。

1.2滑移信息熵的提出

对于一维时间序列，其数据值范围并不确定，按信息熵定义计算存在困难，一般采用分块统计近似计算；另一方面，利用信息熵区分信号冲击主导区域与非冲击主导区域，截断信号必须包含足够的信息量，即信号长度不能太短，然而截断长度也不宜过长，过长将大大降低不同信号区域识别能力。因此，我们需要寻找一种能够充分挖掘截断信号信息并易于计算其信息熵的方法。基于以上，本文引入相空间重构理论，对截断时间序列进行Hankel矩阵构建，形成多维矩阵信号[12]。具体矩阵构建公式如下：

(2)

式中:p代表滑移距离，定义L=2n为截断长度。然后对所得的Hankel矩阵进行归一化操作，将其转变为灰度图像。由于灰度值的范围是0～255，因此只要根据像素灰度值出现的概率，就可以计算出信息熵。本文定义滑移信息熵序列：

H={H(A1),H(A2),…H(Am)}

(3)

式中:m为滑移信息熵序列的长度;截断长度L、原时域序列总长度N和滑移距离p之间的关系满足如下表示：

m=[(N-L)/p]

(4)

式中‘[]’符号表示向下取整。为防止出现截取“泄漏”的现象，进而造成分析结果的失真，所定义的滑移参数p必须在如下公式限定范围：

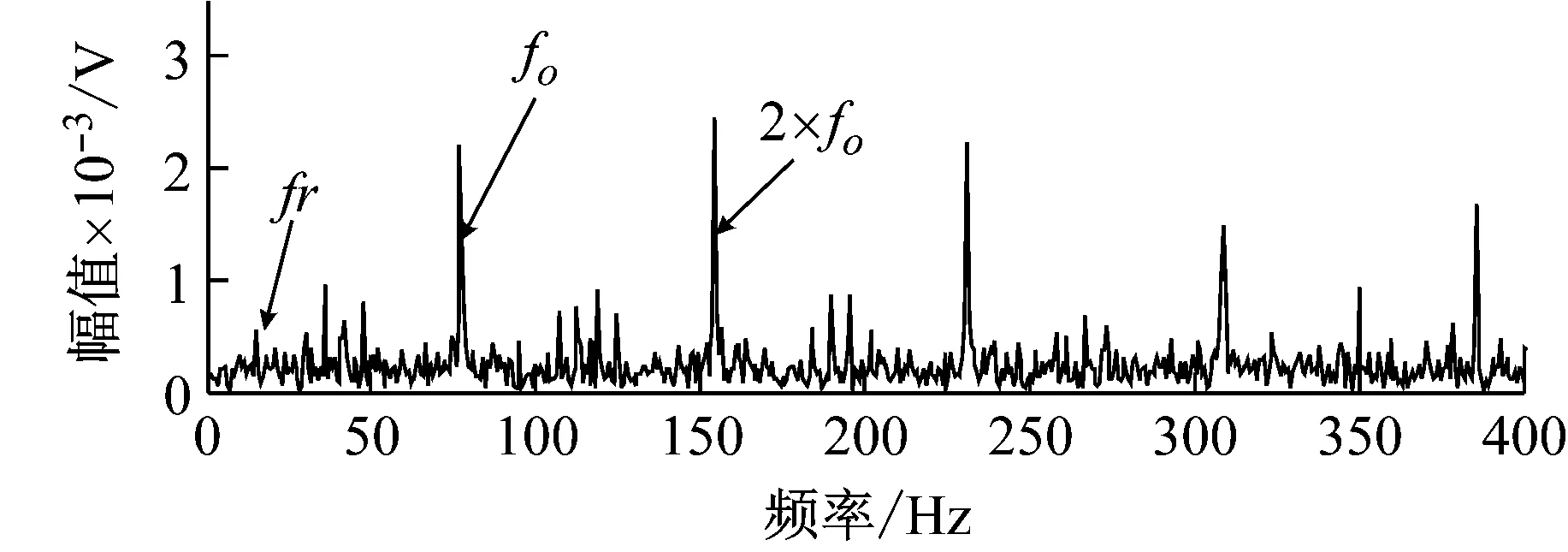
0

(5)

为考察本文提出滑移信息熵对冲击振动信号的特征提取作用，采用式(6)的滚动轴承故障仿真模型获得滚动轴承内圈故障信号，其中冲击信号采用指数衰减振荡进行模拟。

(6)

图1(a)为仿真信号，信噪比为-2 dB。图1(b)为基于Hankel矩阵构建获得的滑移信息熵序列，从图中可以清楚看到在振动冲击剧烈的位置，相对应的信息熵出现较大的幅值下降现象，相邻信息熵“峰谷”之间间隔正好是内圈故障通过周期。

而基于一维信号近似计算得到的滑移信息熵序列，如图1(c)所示，可以看到其表现出一定的冲击特性，但周期性并不明显。该结果证明了本文提出的滑移信息熵序列能够有效提取冲击特征，且多维矩阵更能充分挖掘截断信号所包含的信息。在实际应用中，滑移信息熵的冲击特征提取能力会随着背景噪声的增大而受到干扰，因此需要在其基础上进一步提升性能。

1.3最优滤波器构建

以上分析可知，滑移信息熵能够识别振动信号中的冲击主导区域，并且当H值越小，代表着该处的冲击成分越强烈。因此，通过查找最小信息熵值，我们可以反向重构振动信号中的强冲击成分，具体计算公式如下所示：

(7)

(a) 仿真信号

(b) 矩阵滑移信息熵

(c) 一维滑移信息熵

获得重构冲击成分后，再对其进行频域分析。由于冲击成分可以近似为指数型衰减振荡波形，其频率信息与FIR带通滤波器高度相似。另一方面，故障信号中的冲击成分中往往包含着丰富的故障信息。因此，我们可以已重构冲击成分为基础，通过构建最优滤波器，达到故障特征提取的目的。最优滤波器计算公式如下：

(8)

式中:Y(k)是重构冲击成分的频谱表达式;fs代表采样频率;fc是最优滤波器的中心频率;△f是最优滤波器的带宽。

需要注意的是fs/L表示了重构冲击成分频谱的分辨率。截断长度太小会导致频谱分辨率过大，而过大的频率分辨率会导致所获得的中心频率存在误差，从而影响最终的故障冲击识别效果。此外，截断长短必须满足L

1.4故障诊断技术流程

为尽可能提高最终的故障提取效果，在构建滑移信息熵序列前还需对故障信号进行预处理。考虑到最小熵反卷积(MED)能够过滤信号中的噪声和不确定信号，增强信号中的冲击成分，因此我们使用MED对信号进行预处理[13]。MED基本原理如下：

1) 该过程目标是找到使输出信号y的峭度达到最优的滤波器系数向量w：

(9)

2) 反向滤波的卷积表达式如下：

(10)

3) 当最优滤波器系数达到最优时，目标函数满足：

(11)

4) 由于∂x[n]/∂w[l]=y(n-1), 联立方程可得：

(12)

由此可以得到w=A-1b，该方程可以通过迭代求解获得最优w，实现MED滤波性能。综合以上内容，基于滑移信息熵与最优滤波器构建的故障诊断方法流程图如图2所示。下一章，将对该方法的故障特征提取性能进行验证。

图2 特征提取算法流程

2 方法论证

2.1仿真信号论证

为验证本文提出方法在强背景噪声影响下的故障特征提取能力，通过公式(6)构建信噪比为-8 dB的轴承内圈故障仿真信号如图3(a)所示。在振动信号的时域波形中，在强背景噪声干扰下很难分辨出故障冲击信号。图3(b)是通过本文提出方法处理的信号，从图中可以清楚的分辨出周期性的冲击信号，并且具有幅值调制现象，为明显的内圈故障振动信号。

图4是对以上仿真故障信号处理过程中的中间结果。图4(a)为重构冲击成分，呈现出明显的脉冲振荡衰减特征。可见滑移信息熵方法能够准确的识别振动信号中被噪声淹没的冲击信号。图4(b)是重构冲击成分频谱图，频域结构与带通滤波器频域结构高度一致。在此例中，截断长度L为128，滑移参数p为64，图4(b)所得的频谱分辨率为200 Hz，构建的最优滤波器的中心频率为4 000 Hz,带宽为200 Hz。该例结果证明了本文提出方法对仿真故障信号的故障特征提取效果明显。

(a) 内圈仿真故障信号信噪比为-8 dB

(b) 最优滤波结果

Fig.3 Simulated inner race fault siganl with SNR=-8 dB, the filtered signal

(a) 重构冲击成分

(b) 相应频域响应

Fig.4 Reconstructed impulse component and the corresponding spectrum response

2.2实验信号论证

为论证本文提出的特征提取技术对实际故障信号的诊断作用，特利用滚动轴承试验台对型号为30304的圆柱滚子轴承进行故障模拟实验。采用电火花加工技术模拟外圈点蚀故障。试验装置示意图如图5和6所示，其主要包括控制系统、传动系统和信号采集系统三大部分。该试验台振动加速度传感器型号为LC0152T，采集卡为NI9234，系统采样频率为2.56 kHz。齿轮箱输入转速为900 r/min，转频为15 Hz，滚动轴承转子数为13，经计算外圈故障通过频率(BPO)为75.78 Hz。

图5 轴承加载示意图

图6 实验装置示意图

选取一组外圈故障信号，如图7(a)所示，从振动信号时域波形中很难分辨出淹没在背景噪声中的振动冲击成分。再对其进行包络谱分析，结果如图7(b)所示。在包络谱中除了转频及其两倍频外，无法提取到任何的故障信息，说明该振动信号中的故障冲击成分比较微弱。

(a) 外圈故障信号时域波形

(b) 对应包络谱

针对图7所示的微弱故障信号，利用本文提出的方法进行故障冲击特征提取的最优滤波操作。此例中，截断长度L取256，滑移参数p取128。图8(a)是重构冲击成分，可见对被噪声淹没的冲击提取非常准确。图8(b)是其相应的频域响应，其频率分辨率为100 Hz，峰值为6 800 Hz。构建的最优滤波器中心频率取6 800 Hz，带宽为100 Hz，然后对原始信号进行滤波操作。

(a) 重构冲击成分

(b) 相应频域响应

Fig.8 Reconstructed impulse component and the corresponding spectrum response

滤波后的信号波形如图9(a)所示，冲击信号成分在时域波形上非常明显, 其峭度值为16.83。再对其进行包络谱分析，分析结果如图9(b)所示。在频谱图上，除了转频外还能清楚的识别出外圈故障频率及其倍频。为证明本文方法的可靠性和有效性，特与谱峭度(Spectrum Kurtosis)方法进行对比。图10(a)为快速谱峭度图，取滤波器中心频率为8 000 Hz，带宽为3 200 Hz，所得滤波器频带覆盖本文方法获得的最优滤波器。图10(b)为滤波后信号波形，冲击信号成分明显，其峭度值为15.45，与本文方法获得的结果高度相似。分析结果表明，本文提出的方法能够有效的提取振动信号中的冲击特征，并成功实现滚动轴承故障诊断。

(a) 最优滤波信号

(b) 相应频域响应

(a) 快速谱峭度图

(b) 滤波信号

为进一步说明引入的MED预处理对本文提出故障诊断方法的影响，对图7所示信号直接进行分析，其所得的重构冲击成分如图11(a)所示，与图8(a)比较冲击特征并不显著。图11(b)是故障信号的最终滤波结果，从其波形图依然无法清楚地识别故障冲击成分。该结果证明基于MED的信号预处理对本文提出的滑移信息熵的特征提取有很大的提升作用。

(a) 重构冲击成分

(b) 最优滤波信号

3 结 论

本文通过对故障振动信号进行滑移截断处理，获得滑移信息熵序列，成功实现对振动信号冲击特征的快速识别。在此基础上，结合最小熵反卷积理论和最优滤波器构建方法，实现对滚动轴承微弱故障的精确诊断。通过仿真数据和实验数据分析，可以得到如下结论：本文提出的基于滑移信息熵和最优滤波器构建的故障特征提取技术对故障冲击拥有较好的识别提取作用。通过对比研究发现，MED预处理对本文提出故障诊断方法有较大的提升作用。

[1] RANDALL R B, ANTONI J. Rolling element bearing diagnostics—a tutorial[J]. Mechanical Systems and Signal Processing,2011, 25(2): 485-520.

[2] CONG Feiyun, CHEN Jin, DONG Guangming, et al. Short-time matrix series based singular value decomposition for rolling bearing fault diagnosis[J]. Mechanical Systems and Signal Processing,2013, 34(1): 218-230.

[3] XU J, TONG S, CONG F, et al. The application of time-frequency reconstruction and correlation matching for rolling bearing fault diagnosis[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,2015, 229(17): 3291-3295.

[4] PINCUS S M. Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Sciences,1991, 88(6): 2297-2301.

[5] RICHMAN J S, MOORMAN J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278(6): H2039-H2049.

[6] 杨文献, 姜节胜. 机械信号奇异熵研究[J]. 机械工程学报,2000,36(12): 9-13.

YANG Wenxian, JIANG Jiesheng. Study on the singular entropy of mechanical signal[J]. Chinese Journal of Mechanical Engineering,2000, 36(12): 9-13.

[7] 张雨, 胡茑庆. 基于符号树信息熵的机械振动瞬态信号特征提取[J]. 国防科技大学学报,2003,25(4): 79-81.

ZHANG Yu, HU Niaoqing. Extraction of the characteristic of mechanism vibration transient signal based on entropy of symbolic tree[J]. Journal of National University of Defense Technology,2003, 25(4): 79-81.

[8] YANG Yu, CHENG Junsheng. A roller bearing fault diagnosis method based on EMD energy entropy and ANN[J]. Journal of Sound and Vibration,2006, 294(1): 269-277.

[9] 夏勇, 赵红. 基于关联距离熵的诊断方法研究[J]. 振动与冲击,2003,22(2): 78-79.

XIA Yong, ZHAO Hong. Leakage fault diagnosis for valve train based on correlation distance entropy[J]. Journal of Vibration and Shock,2003, 22(2): 78-79.

[10] YU Dejie, YANG Yu, CHENG Junsheng. Application of time-frequency entropy method based on Hilbert-Huang transform to gear fault diagnosis[J]. Measurement,2007, 40(9/10): 823-830.

[11] 郑近德, 陈敏均, 程军圣, 等. 多尺度模糊熵及其在滚动轴承故障诊断中的应用[J]. 振动工程学报,2014,27(1): 145-151.

ZHENG Jinde, CHEN Minjun, CHENG Junsheng, et al. Multiscale fuzzy entropy and its application in rolling bearing fault diagnosis[J]. Journal of Vibration Engineering,2014, 27(1): 145-151.

[12] ZHAO X, YE B. Selection of effective singular values using differences pectrum and its applicationt of fault diagnosis of headstock[J]. Mechanical Systems and Signal Processing,2011, 25: 1617-1631.

[13] ENDO H, RANDALL R B. Application of a minimum entropy deconvolution filter to enhance Autoregressive model based gear tooth fault detection technique[J]. Mechanical Systems and Signal Processing,2007, 21(2): 906-919.

Faultdiagnosismethodbasedontheslipinformationentropyandoptimalfilterconstruction

TONGShuiguang1,XUJian2,CONGFeiyun1,TANGNing2,ZHANGYidong1

(1. Institute of mechanical design and automation, Zhejiang University, Hangzhou 310027, China; 2. Institute of Thermal Science and Power Engineering, Zhejiang University, Hangzhou 310027, China)

Based on the difference in local feature of fault signal， the concept of slip information entropy sequence was put forward and combined with the phase space reconstruction and information entropy theory to detect the local impulse feature informations. The minimum entropy deconvolution, optimal filter construction theory were applied to improve the ability of weak fault diagnosis. The proposed method has been successfully applied in the fault feature extraction of rolling bearings. The experimental data analysis results show that the proposed method has a good ability of weak shock fault feature extraction. The work has important implications in fault intelligent diagnosis of rolling bearings under strong noise background.

information entropy; slip interception; optimal filter; feature extraction; rolling bearing

TH165.3；TN911；TH17

A

10.13465/j.cnki.jvs.2017.21.006

国家自然科学基金(51305392);浙江省自然科学基金(LZ15E050001);流体传动与控制国家重点实验室青年基金(SKLoFP_QN_1501)

2016-03-30 修改稿收到日期：2016-07-22

童水光 男,博士后,教授,博士生导师,1960年9月生