手性和反手性蜂窝材料的面内冲击性能研究

卢子兴， 李 康

(北京航空航天大学 固体力学研究所，北京 100083)

手性和反手性蜂窝材料的面内冲击性能研究

卢子兴， 李 康

(北京航空航天大学 固体力学研究所，北京 100083)

采用数值模拟方法，研究了具有手性和反手性构型的负泊松比蜂窝(统称手性系蜂窝)在不同冲击速度下的变形模式和能量吸收等动态力学响应特性。结果表明，低速冲击下，其变形模式为连接带和圆孔的先后坍塌；高速冲击下，为圆孔和连接带交替坍塌的逐层压溃；在中等速冲击下，为兼有低速和高速模式部分特征的过渡模式；随着冲击速度的提高，局部变形区逐渐集中于冲击端。并且，在中、低速冲击时，能观察到手性系蜂窝的动态负泊松比效应。此外，数值模拟结果使我们对这类二维负泊松比多孔材料的动态力学性能和能量吸收性能有了一定的认识，同时为进一步研究三维负泊松比泡沫材料的冲击行为奠定了基础。

蜂窝；负泊松比；手性；动态压溃；变形模式

以蜂窝和泡沫形式呈现的负泊松比多孔材料在航空航天和汽车工业领域内有着广泛的应用[1]，如弯曲夹层板的芯材[2]，变形机翼的自适应翼盒[3]，可展开天线反射器[4]，弹性座垫缓冲材料，能量吸收元件等。与普通多孔材料相比，负泊松比多孔材料具有更高的冲击阻抗、抗剪能力、抗凹能力和能量吸收性能等，已引起了国内外学者的广泛关注[5-8]。手性系蜂窝作为负泊松比多孔材料之一，国外学者已对其在静态加载下的力学行为进行了大量的理论分析、数值模拟和试验等研究[9-10]，发现手性系蜂窝的面内弹性模量和泊松比依赖于其拓扑结构，而且其变形机制结合了圆形节点的旋转和连接带的弯曲变形。并且，指出理论模型未考虑面内剪切应变，对于手性系蜂窝，轴向变形与剪切变形在面内耦合，当剪切应变不为零时，在轴向应力作用下，面内剪切进一步扩展，表现出非经典的Cosserat弹性或微极弹性。随后，为准确模拟轴向变形与剪切变形的耦合，Spadoni等[11]采用微极连续介质模型，Dos Reis等[12]借助于离散的渐进均匀化方法，分别对手性系蜂窝的弹性性能进行了分析。当前的研究主要集中于预测手性系蜂窝静态力学性能和解释负泊松比行为的形成机制上，而对于其在冲击载荷作用下的动力学性能的研究还未深入展开。当结构的惯性不能忽略，并且材料表现出应变率效应时，手性系多孔结构在高应变率加载下的力学响应与静载荷下响应的差异，仍需要加以研究。

本文通过数值计算，分析手性系蜂窝材料在面内动态冲击下的变形模式和能量吸收等动态力学响应特性，探讨手性几何拓扑对负泊松比多孔材料的动态力学响应的影响，尤其是胞元的微结构是如何影响蜂窝材料的局部动态应力演化，进而影响其整体动态力学响应的问题。本文为揭示手性系蜂窝的动态变形机理奠定了基础，同时为负泊松比多孔材料的设计和应用提供一定意义上的指导。

1 模型的建立

1.1手性系蜂窝的几何结构参数

图1中显示了代表性的四边反手性蜂窝的几何结构参数，其中l，r，t分别代表连接带的长度，圆形节点的半径及其壁厚，连接带和圆形节点的壁厚相同。为比较连接带对手性系蜂窝的力学性能的影响，各个蜂窝结构采用相同的连接带长度和圆形节点半径，只改变胞壁厚度以保持相同的相对密度，如以四边反手性蜂窝为例，可取l=20 mm，r=5 mm，t=1.2 mm。

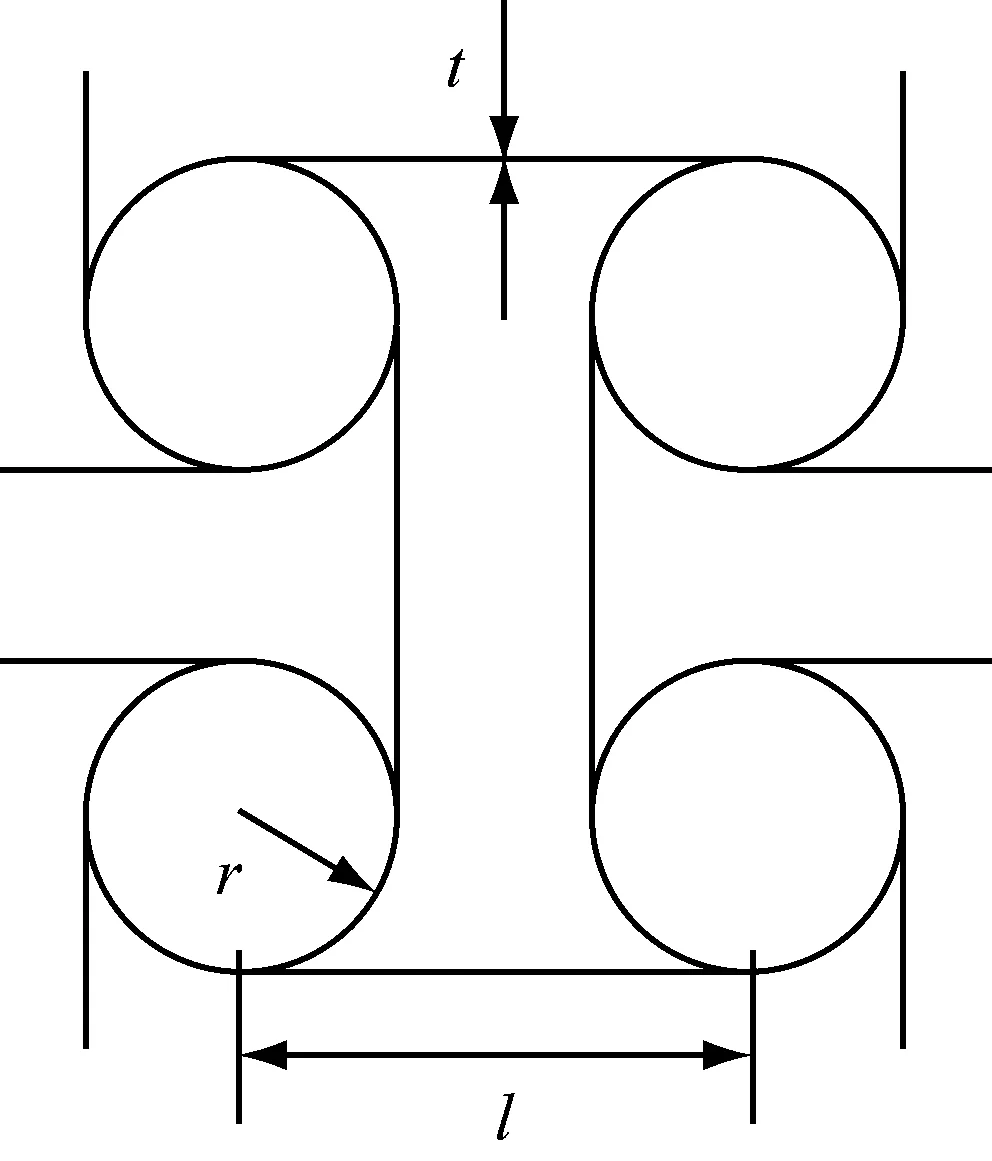
图1 四边反手性蜂窝单元的几何参数

Fig.1 Diagram of anti-tetrachiral cell showing geometric parameters

1.2有限元模型

本文使用ANSYS/LS-DYNA显式动力分析有限元软件对手性系蜂窝材料面内冲击特性进行了数值分析。基体材料选用金属Al，假定为理想弹塑性的，其材料参数分别为：弹性模量Es=69 GPa，屈服应力σys=76 MPa，密度ρs=2.7×103kg/m3，泊松比νs=0.3。胞壁选用SHELL163壳单元，采用全积分Belytschko-Tasy壳单元算法。为了收敛性需要，沿厚度方向定义五个积分点。另外，计算中对蜂窝模型采用单面自动接触算法，刚性板表面与蜂窝的外表面采用面-面接触，摩擦因数设置为0.25。手性系蜂窝材料的刚性板面内冲击计算模型如图2所示。

图2 手性系蜂窝材料的面内冲击加载示意图

图3为手性系蜂窝材料填充胞元模型，其中(a)为六边手性蜂窝材料模型，在水平和竖直方向的尺寸分别为211.2 mm和203.6 mm。(b)为四边反手性蜂窝材料模型，在两个方向的尺寸均为190 mm。(c)为三边手性蜂窝材料模型，在水平和竖直方向的尺寸分别为319.8 mm和323.0 mm。(d)为三边反手性蜂窝材料模型，在水平和竖直方向的尺寸分别为287.1 mm和290 mm。蜂窝模型放置在上、下两个刚性板中间，计算过程中下刚性板固定，上刚性板以一定初速度向下冲击蜂窝，速度范围取2～140 m/s。计算中限制整个蜂窝模型所有节点的面外位移，以保证平面应变状态。

(a) 六边手性蜂窝材料模型

(b) 四边反手性蜂窝材料模型

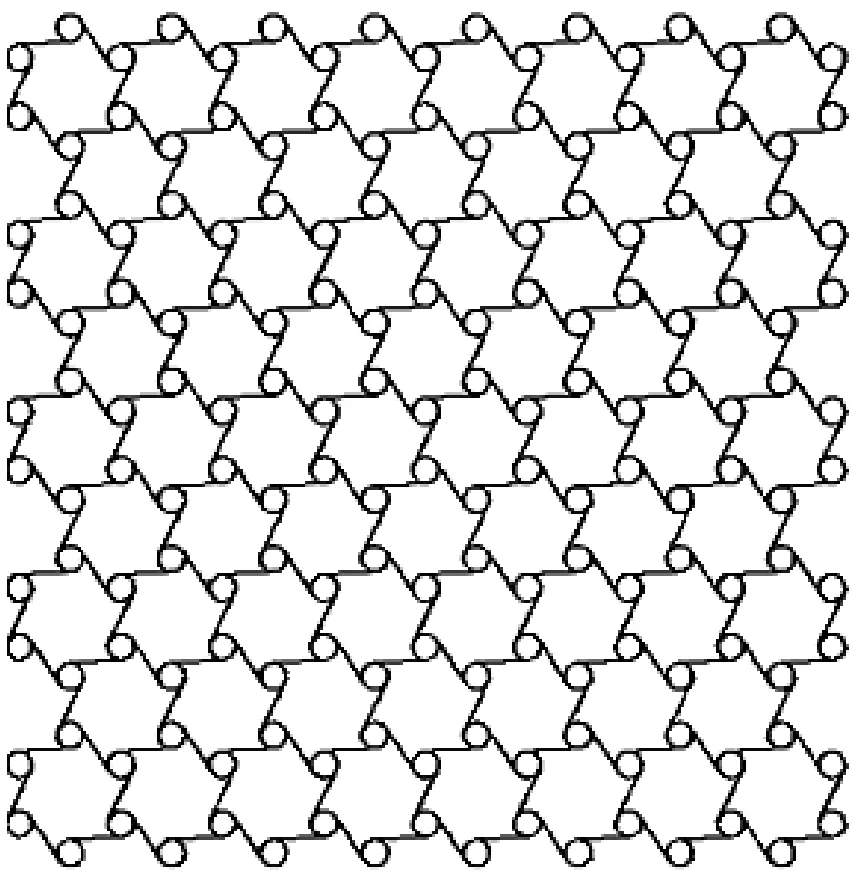
(c) 三边手性蜂窝材料模型

(d) 三边反手性蜂窝材料模型

2 模拟结果和讨论

2.1手性系蜂窝材料的动力响应

基于上述计算模型，探讨了由连接带和圆形节点构成的但连接方位和数目不同的手性系蜂窝材料在具有一定初速度(2～140 m/s)的刚性板冲击下的动态响应。图4～11分别给出了低速、中速和高速冲击下手性系蜂窝材料的典型动态响应过程，反映了从准静态到高应变率范围内蜂窝材料的变形特性。

Ruan等[13]的分析表明，六边形蜂窝材料在面内低速冲击下，表现为“V”形坍塌带, 高速时表现为“I”形坍塌带，而手性系蜂窝在面内不同冲击速度下的变形模式与六边形蜂窝有所不同。

2.1.1 六边手性蜂窝材料的动力响应

图4给出了六边手性蜂窝材料在不同冲击速度下的典型变形过程，蜂窝材料冲击端的动态响应,如图5所示。

ε=0．05ε=0．25ε=0．4ε=0．6V=2m/sV=28m/sV=100m/s

图4 不同冲击速度下六边手性蜂窝材料变形模式

Fig.4 Deformation modes of hexachiral honeycombs under different impact velocities

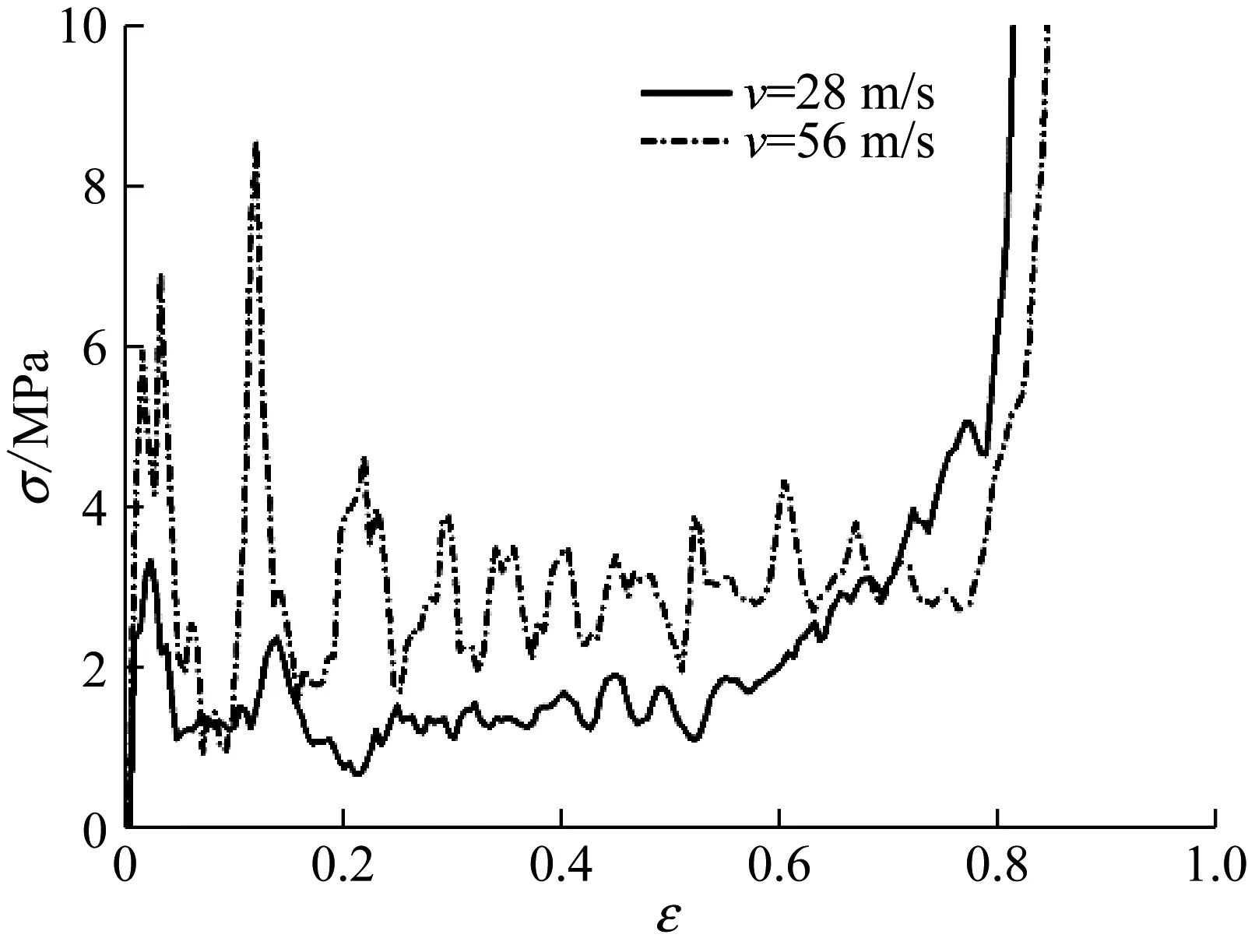
图5 不同冲击速度下六边手性蜂窝材料冲击端的名义应力-应变曲线

Fig.5 Nominal stress-strain curves for the impact end of hexachiral honeycombs under different impact velocities

刚性板的冲击速度为2 m/s时，模拟结果接近准静态加载的情况。可以看到，模型的中部首先产生变形，紧接着由于连接带的弯曲，带动圆形节点旋转，两者相互卷绕，向四周扩展，遍布每一个胞元。弯曲卷绕导致整个模型发生均匀的横向收缩，表现出典型的负泊松比行为，胞壁的间距不断减小，圆形节点开始互相接触。随着压缩的进一步进行，圆形孔壁开始逐渐屈曲进而坍塌，进入密实化阶段。整个变形过程可以分为两个阶段，第一个阶段为连接带的弯曲卷绕和圆形节点的旋转，第二个阶段为圆形孔壁的坍塌，两个阶段的变形都表现得很均匀。

随着冲击速度的继续增加，在28 m/s时，结构中的应力超过弹性屈曲极限后，应力达到初始峰值(见图5)。靠近冲击端的胞元首先产生局部变形，包含圆形节点的坍塌以及连接带的弯曲变形。随着压缩的持续，冲击端可以明显地看到连接带卷绕在圆形节点上，模型开始产生局部收缩。随后，整个模型的胞元中几乎都产生了连接带的弯曲卷绕和圆形节点的转动，而这正是手性蜂窝产生负泊松比行为的原因(参见文献[5])。

此外，可以看到在模型的相对压缩量接近50%时，在垂直于加载方向上，模型的中部产生了明显的横向收缩，可形象地称之为“缩颈”现象。该模型给出的负泊松比行为解释了交错排布的三角形和正方形蜂窝在中低速冲击下所表现出的颈缩现象[14-15]。

冲击速度进一步增加到100 m/s时，变形模式表现的更加局部化，表现为与普通蜂窝材料一致的高速冲击下的“I”形变形模式。局部变形带自冲击端一层一层向下传播至固定端，直到压缩密实。此时，蜂窝中几乎观察不到负泊松比现象。

2.1.2 四边反手性蜂窝材料的动力响应

图6给出了四边反手性蜂窝材料在不同冲击速度下的典型变形过程，蜂窝材料冲击端的动态响应如图7所示。

当冲击速度为2 m/s时，在线弹性区，模型变形均匀。随着应力进一步增加，模型中部靠下位置首先产生局部变形。进而，连接带产生较大的弯曲，迫使圆形节点产生旋转，引发其他连接带弯曲，两者相互卷绕，导致模型发生局部横向收缩，表现出负泊松比行为。由于模型发生了整体的屈曲，在局部变形带中，胞元表现出不对称的剪切坍塌模式。此时，整个变形过程仍分为两个阶段。

ε=0．05ε=0．25ε=0．4ε=0．6V=2m/sV=28m/sV=100m/s

图6 不同冲击速度下四边反手性蜂窝材料变形模式

Fig.6 Deformation modes of anti-tetrachiral honeycombs under different impact velocities

当冲击速度为28 m/s时，局部变形区首先在冲击端形成，产生了初始的应力峰值(图7)，伴随着大量的连接带弯曲卷绕和圆形节点转动，导致模型产生局部收缩。随着冲击的持续，模型的中部产生了明显的横向收缩。随后，圆形孔壁开始持续坍塌，直至整个蜂窝模型被完全压溃。

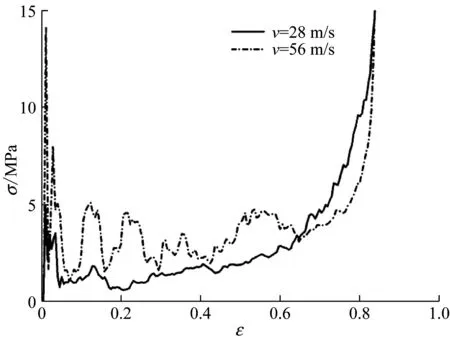
图7 不同冲击速度下四边反手性蜂窝材料冲击端的名义应力和应变曲线

Fig.7 Nominal stress-strain curves for the impact end of anti-tetrachiral honeycombs at different impact velocities

随着冲击速度继续提高到100 m/s时，“I”形变形模式表现得更加充分，几乎观察不到连接带卷绕圆形节点的行为，而是胞元被逐层压溃。

四边反手性蜂窝材料动态响应的显著特点是，“缩颈”现象持续存在于不同速度的冲击下。

2.1.3 三边手性蜂窝材料的动力响应

图8给出了三边手性蜂窝材料在不同冲击速度下的典型变形过程，蜂窝材料冲击端的动态响应如图9所示。

刚性板的冲击速度为2 m/s时，不同于六边和四边反手性蜂窝，三边手性蜂窝在固定端首先产生局部变形。随着压缩位移进一步增加，模型中部产生了第二个局部变形带。进而更多的胞元进入局部变形带，在整个模型中得到扩展。随着进一步压缩，进入到密实化阶段。整个变形过程仍分为两个阶段，连接带的弯曲卷绕和圆形孔壁的坍塌，但是没有观察到模型的负泊松比效应。

当冲击速度增加到28 m/s时，靠近冲击端的第一行胞元首先开始变形。随着刚性板的压缩，自冲击端开始，胞元被逐层压溃，变形模式比较单一，只包含水平位置连接带的弯曲和竖直连接带的卷绕，以及由连接带的卷绕带动圆形节点的转动。胞元中的间距不断减小，胞壁开始互相接触，直至圆形节点完全堆积，圆形孔壁才开始坍塌，一直持续到模型被完全压溃。值得注意的是整个变形过程表现得比较均匀，未见到模型局部收缩。正是这种均匀的变形模式，使得蜂窝材料的临界应力值达到弹性极限应力之后，试件进入了稳定的平台应力阶段，如图9所示。

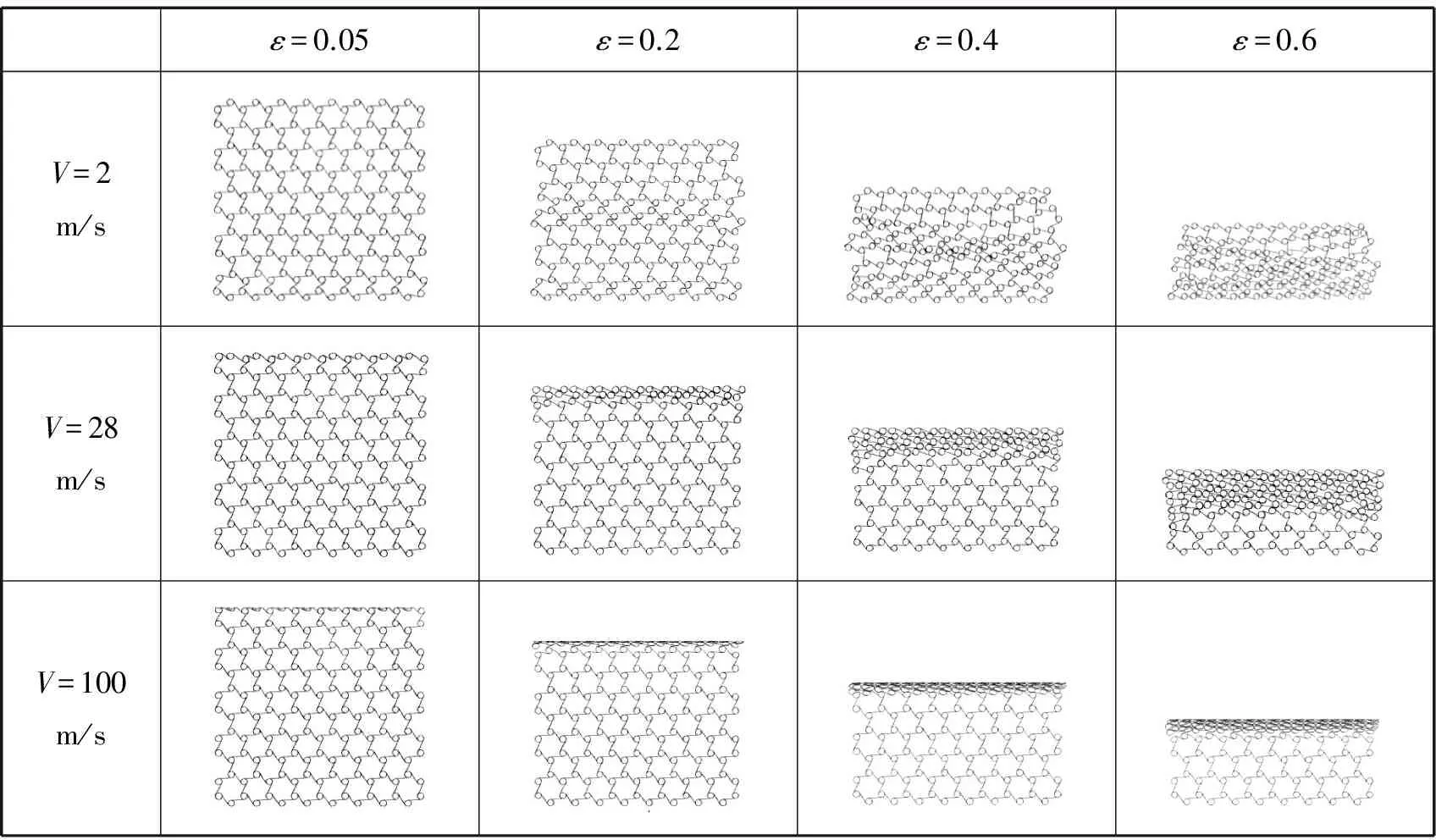
ε=0．05ε=0．2ε=0．4ε=0．6V=2m/sV=28m/sV=100m/s

图8 不同冲击速度下三边手性蜂窝材料变形模式

Fig.8 Deformation modes of trichiral honeycombs under different impact velocities

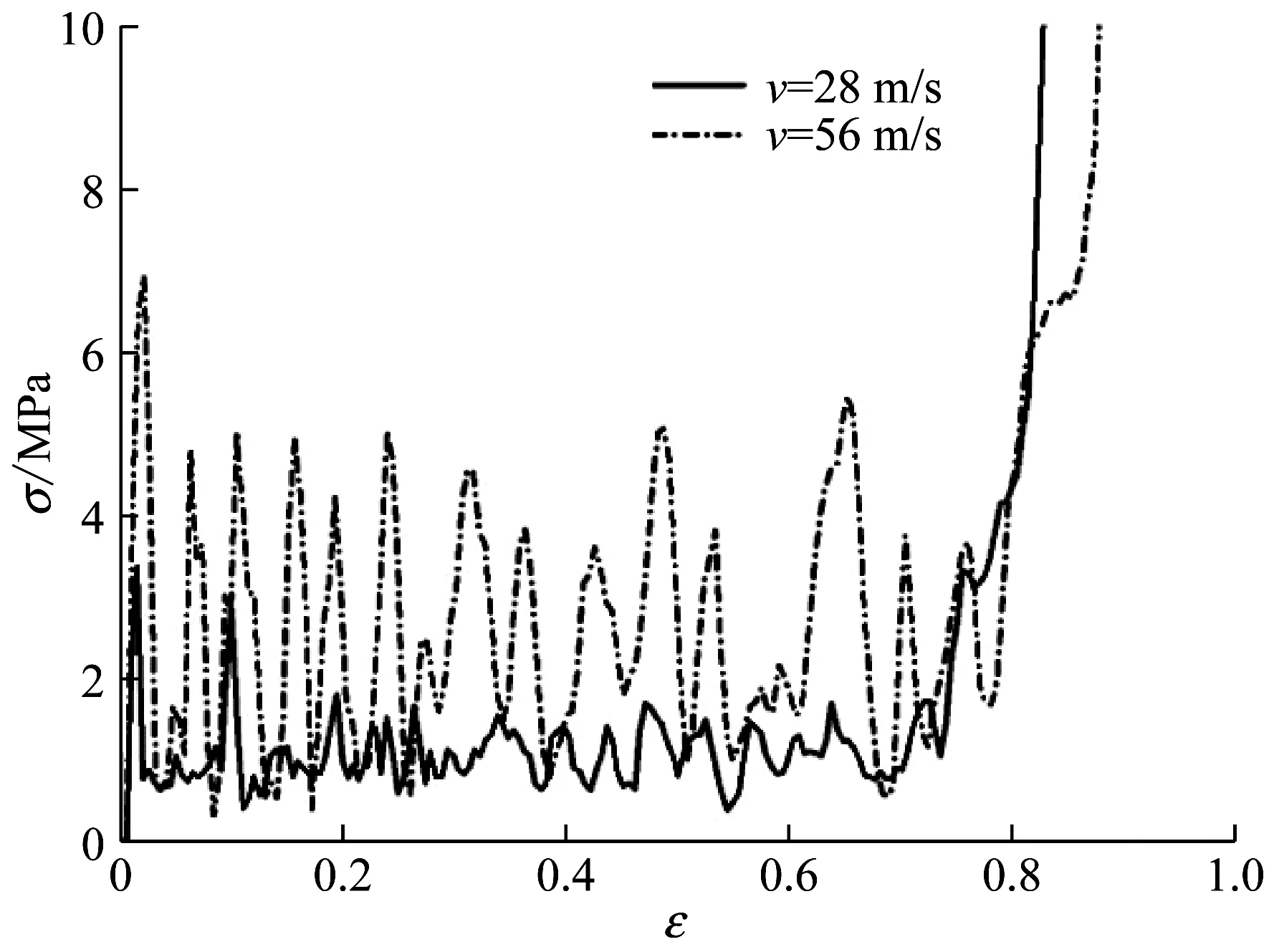
图9 不同冲击速度下三边手性蜂窝材料冲击端的名义应力和应变曲线

Fig.9 Nominal stress-strain curves for the impact end of trichiral honeycombs under different impact velocities

冲击速度增加到100 m/s时，变形模式更加单一，表现为层层压溃的“I”形变形模式。

2.1.4 三边反手性蜂窝材料的动力响应

图10给出了三边反手性蜂窝材料在不同冲击速度下的典型变形过程，蜂窝材料冲击端的动态响应如图11所示。

当冲击速度为2 m/s时，在线弹性范围，模型产生了均匀变形。随着压缩位移进一步增加，中部靠下位置产生了一个横贯模型的局部剪切变形带。局部变形区内主要为连接带的弹性屈曲和弯曲变形，迫使圆形节点产生旋转，继而引发其他连接带弯曲，使局部变形带沿着刚度软化的方向传播。应变进一步增大，更多的连接带发生弹性坍塌，圆形节点的孔壁开始互相紧密接触，模型产生显著的横向收缩。随着进一步压缩，圆形孔壁才开始逐渐坍塌，进入密实化阶段。

冲击速度为28 m/s时，冲击端首先产生局部变形，竖直位置的连接带发生了弹性屈曲，在图11中形成了第2个应力峰值。随着压缩的进行，连接带弯曲使圆形节点产生转动，圆形节点转动又诱导连接带产生弯曲，这两种变形互相影响，在第3-5个应力峰值之后，引起蜂窝结构发生软化，应力峰值降低。刚性板继续压缩，这种变形模式均匀地扩展至固定端后，圆形孔壁坍塌，变形进入密实化阶段。可以观察到模型中部存在局部收缩，相比于低速时有很大的减弱。

冲击速度为100 m/s时,惯性效应进一步增强，自冲击端开始，胞元被逐层压溃。随着冲击速度的进一步增加，逐层压溃表现得更加充分，模型中几乎观察不到收缩现象。

综上所述，比较不同手性和反手性拓扑构型蜂窝在面内冲击下的变形模式，可以发现，在低速冲击时，手性系蜂窝的变形分为两个阶段：第一个阶段为连接带的弯曲卷绕和圆形节点的转动，第二阶段为圆形孔壁的坍塌。在高速冲击时，变形表现为圆形孔壁和连接带的交替坍塌，被逐层压溃。在中速冲击下，表现为介于低速模式和高速模式之间，兼有两者部分特征的过渡模式。随着冲击速度的提高，胞壁的变形模式由弹性屈曲向塑性变形转化，局部变形区由固定端逐步发展到冲击端。

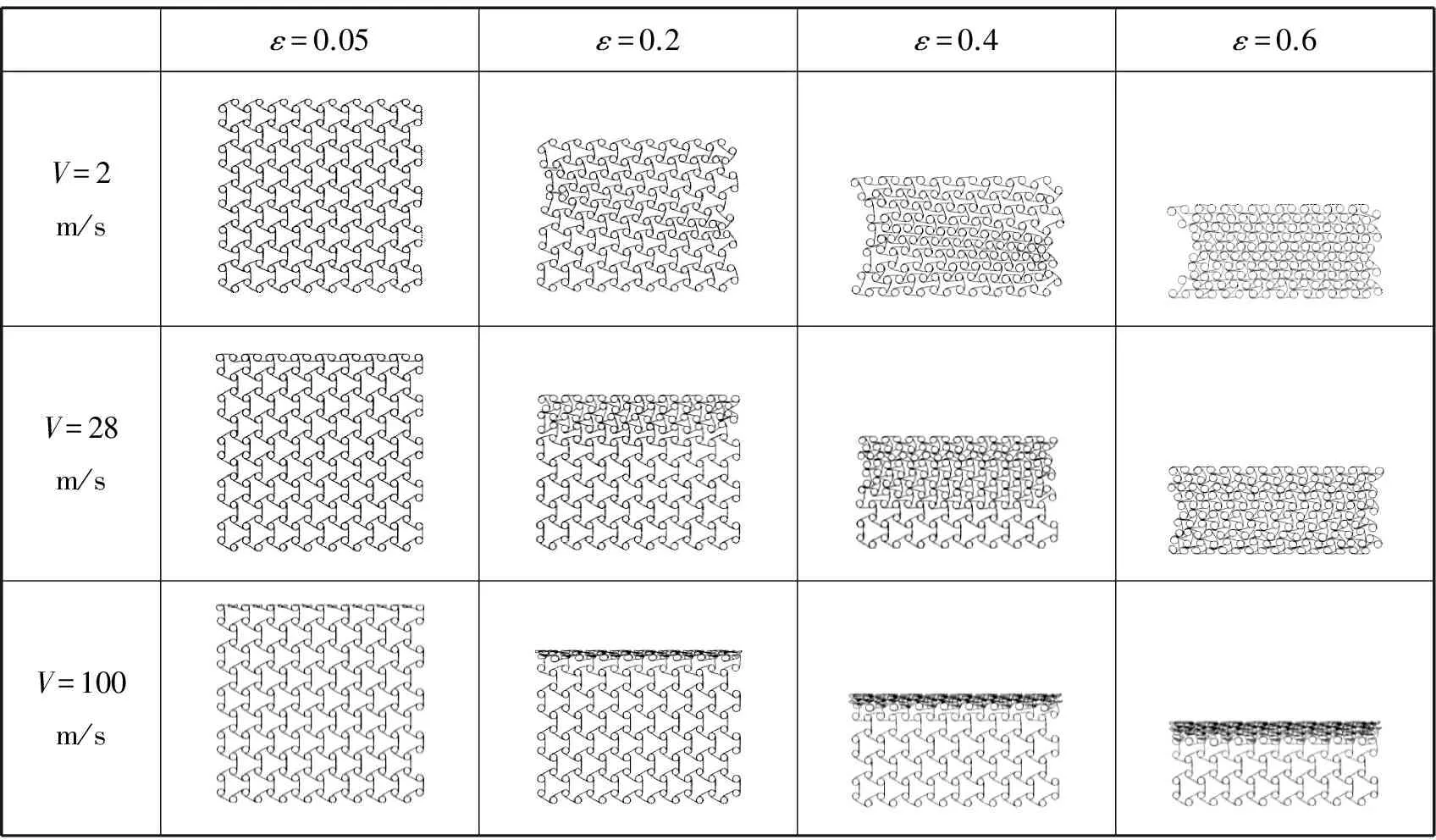
ε=0．05ε=0．2ε=0．4ε=0．6V=2m/sV=28m/sV=100m/s

图10 不同冲击速度下三边反手性蜂窝材料变形模式

Fig.10 Deformation modes of anti-trichiral honeycombs under different impact velocities

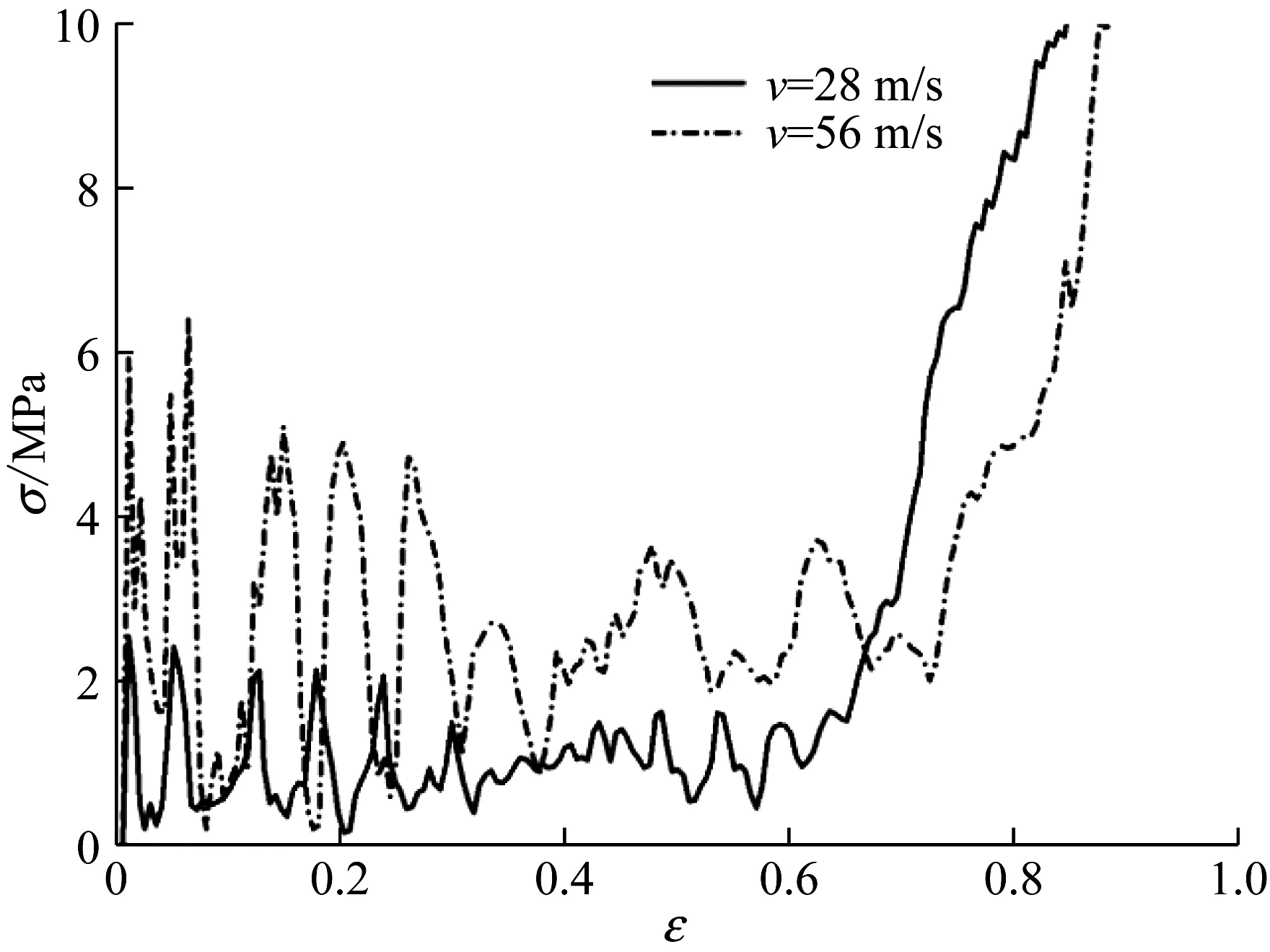
图11 不同冲击速度下三边反手性蜂窝材料冲击端的名义应力和应变曲线

Fig.11 Nominal stress-strain curves for the impact end of anti-trichiral honeycombs under different impact velocities

通过比较不同冲击速度下手性系蜂窝材料冲击端的名义应力-应变曲线，可以看到，初始应力峰值、平台应力和应力平台区长度均随着冲击速度的提高而增加，承载能力更强。动态加载所造成的应力增强,一方面源于冲击速度提高导致的密实化加快，另一方面源于孔壁的微惯性增强。微惯性涉及到孔壁发生屈曲时的旋转和横向运动，倾向于抑制更柔顺的非对称屈曲变形模式，使局部变形区得到传播，提高了压溃应力。

2.2手性系蜂窝的动态泊松比

为了与手性系蜂窝在静态加载下的负泊松比效应作比较，在此定义面内动态加载下，模型的局部横向收缩名义应变与压缩名义应变的负比值中绝对值最大者为动态泊松比，即变形后横截面积最小位置的横向收缩名义应变与压缩名义应变的负比值。并非所有的手性系蜂窝材料在面内冲击下都表现出负泊松比行为，计算结果和分析表明，三边手性蜂窝在不同速度冲击下均没有表现出负泊松比效应。这取决于手性结构的几何拓扑，即连接带与圆形节点的连接方位和数目。不同的手性拓扑使得连接带和圆形节点的相互作用产生不同的效应，应力波在结构中的局部动态传播特性产生了差异，进而导致宏观模型表现出不同的响应特性。

但随着冲击速度的提高，这种在较低应变率范围内呈现出的负泊松比效应会逐渐消失，手性拓扑的影响已不再处于主导地位，这一切源于惯性效应的增强。如图12给出了手性系蜂窝的面内动态泊松比随冲击速度的变化趋势。可以预见，冲击速度进一步增加，动态泊松比会逐渐趋近于零值。

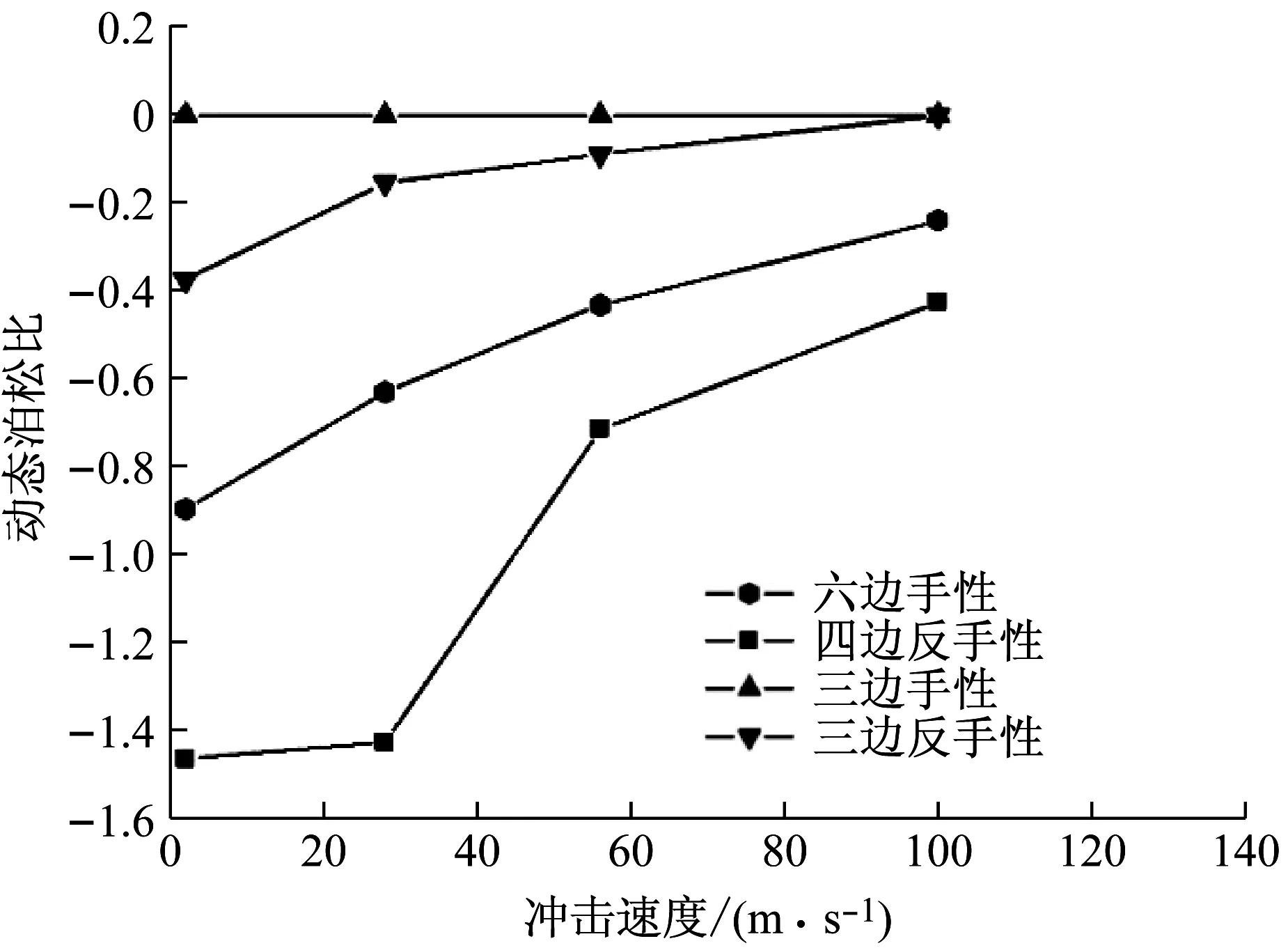
图12 手性系蜂窝材料的动态泊松比随冲击速度的变化趋势

2.3手性系蜂窝材料的能量吸收性能

多孔材料压溃时的典型特征是在初始线弹性响应段后具有一个应力几乎保持不变的平台阶段，它是能量吸收应用中主要关心的变形部分。应力平台的高度和长度决定了多孔材料在承受冲击载荷下的能量吸收效率。

单位体积的蜂窝材料压缩到某一应变时所吸收的能量，即冲击端的名义应力-应变曲线下一直到该压缩应变时的面积[1]

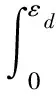
(1)

式中:εd为材料密实化前的某一应变;σ为随应变而发生变化的压缩应力。

基于式(1)，图13给出了在相同相对密度条件下，不同冲击速度下，单位体积的手性系蜂窝材料吸收的能量与名义应变的关系曲线。

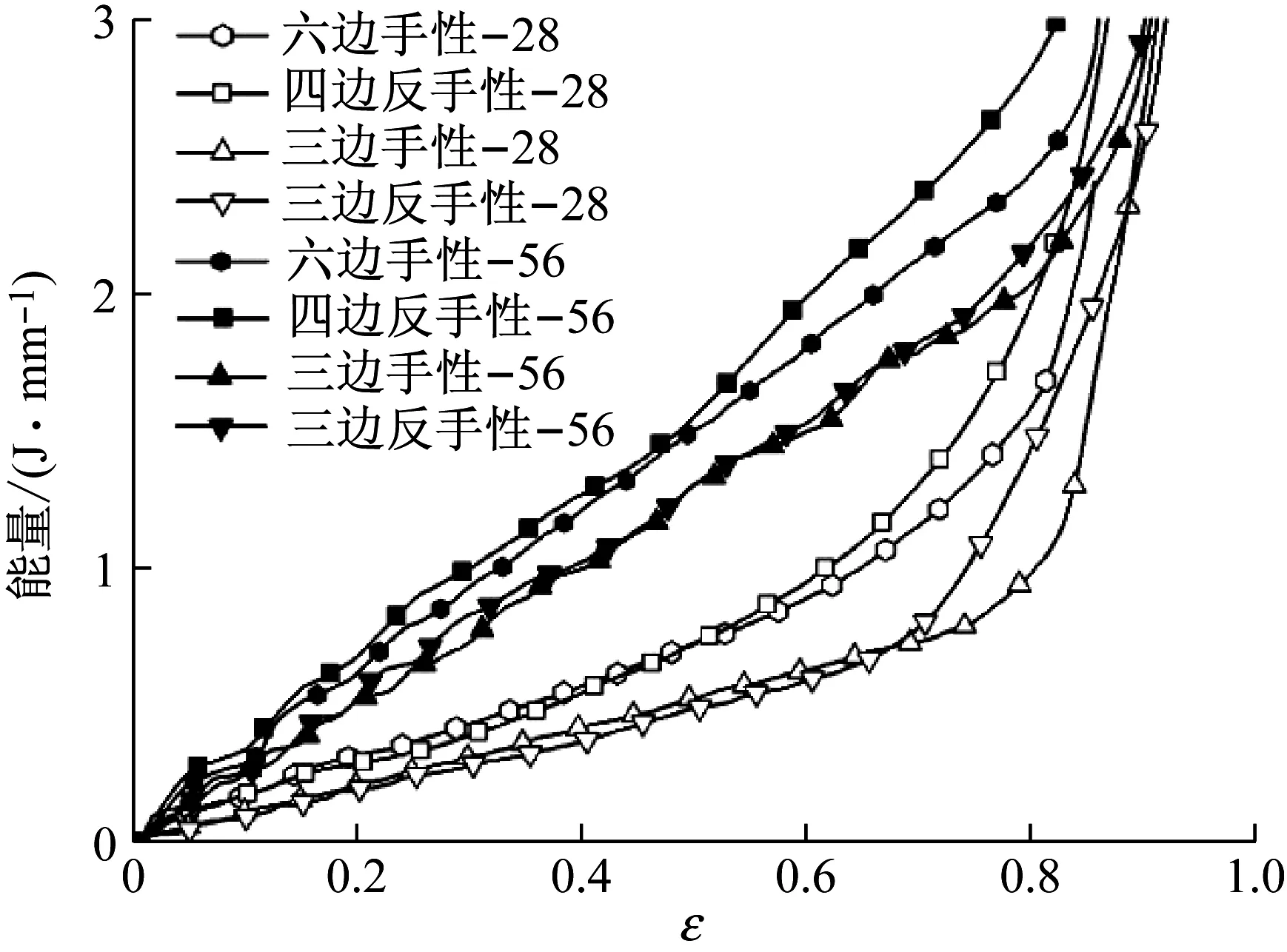
图13 单位体积的不同手性蜂窝材料的能量吸收比较

Fig.13 Energy absorption per volume for chiral and antichiral honeycombs under different impact velocities

上述结果表明，对于相同相对密度的手性系蜂窝材料，在材料的相对压缩量一致的条件下，随着冲击速度的提高，所有的手性蜂窝材料均表现出更强的能量吸收能力，并且四边反手性蜂窝材料的能量吸收能力表现得最强。

可见，手性系蜂窝的拓扑结构对蜂窝材料的动态力学性能的影响非常显著。从手性系蜂窝材料吸收能量的方式看，手性系蜂窝除了发生塑性变形外，还包含圆形节点的转动。圆形节点的转动诱导连接带的弯曲卷绕，使整个蜂窝模型的胞元联动地产生变形，因而能够充分发挥每一个胞元的能量吸收能力。可以预见，由圆形节点的旋转产生的转动动能来吸收一定比例的能量，在手性系蜂窝材料承受中低速冲击时的能量吸收中具有较大的潜质。通过提高圆形节点的旋转动能在吸收能量中的比例，来提高手性系蜂窝材料的能量吸收能力，是多孔材料的能量吸收设计的一个新思路。随着冲击速度的提高，惯性效应的影响变得愈发显著，使得变形局部化，微惯性增强和致密化加快，手性拓扑的影响则大大减弱。

3 结 论

各种不同类型手性系蜂窝材料的变形模式较为一致。在低速冲击下，手性系蜂窝的变形可分为两个阶段：第一个阶段为连接带的弯曲卷绕和圆孔的转动，第二阶段为圆形孔壁的坍塌。在高速冲击下，变形表现为圆形节点和连接带的交替坍塌，胞元逐层压溃。在中速冲击下，则表现为兼有低速和高速模式部分特征的过渡模式。随着冲击速度的提高，局部变形区由固定端逐步发展到冲击端。同时，在中、低速冲击下，部分手性系蜂窝呈现出动态负泊松比效应。

不同的手性拓扑结构使得连接带和圆形节点产生的相互作用大不相同，因此应力波在结构中的局部动态传播特性产生了差异，进而导致宏观模型表现出不同的响应特性，只有六边手性蜂窝和四边反手性蜂窝表现出了明显的动态负泊松比效应，而三边反手性蜂窝的动态负泊松比效应则不那么明显，三边手性蜂窝几乎没有表现出动态负泊松比效应。但随着冲击速度的提高，这种在较低应变率范围内呈现出的负泊松比效应会逐渐消失，手性拓扑的影响减弱，而惯性效应逐渐处于主导地位。

对于相对密度相同的手性系蜂窝材料而言，在材料的相对压缩量一致的条件下，随着冲击速度的提高，所有的手性系蜂窝材料均表现出更强的能量吸收能力，并且，发现单位体积的四边反手性蜂窝材料的能量吸收能力最强。

[1] GIBSON L J, ASHBY M F. Cellular solids: structure and properties(2nd ed.)[M]. Cambridge: Cambridge University Press, 1997.

[2] EVANS K E. Design of doubly curved sandwich panels with honeycomb cores[J]. Composite Structures, 1991, 17(2):95-111.

[3] BORNENGO D, SCARPA F, REMILLAT C. Evaluation of hexagonal chiral structure for morphing airfoil concept[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2005, 219:185-192.

[4] HASSAN M R, SCARPA F, RUZZENE M, et al. Smart shape memory alloy chiral honeycomb[J]. Materials Science and Engineering A, 2008, 481/482:654-657.

[5] LIU Q. Literature Review: materials with negative poisson’s ratios and potential applications to aerospace and defence[R]. DSTO-GD-0472. Australia, 2006.

[6] ALDERSON A, ALDERSON K L. Auxetic materials[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2007, 221:565-575.

[7] 卢子兴, 刘强, 杨振宇. 拉胀泡沫材料力学性能[J]. 宇航材料工艺,2010(1):7-13.

LU Zixing, LIU Qiang, YANG Zhenyu. Mechanical properties of auxetic foams[J]. Aerospace Materials and Technology, 2010(1):7-13.

[8] PRAWOTO Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio[J]. Composites Science and Technology, 2012, 58:140-153.

[9] PRALL D, LAKES R S. Properties of a chiral honeycomb with a Poisson’s ratio-1[J]. International Journal of Mechanical and Science, 1996, 39:305-314.

[10] ALDERSON A, ALDERSON K L, ATTARD D, et al. Elastic constants of 3-, 4- and 6-connected chiral and antichiral honeycombs subject to uniaxial in-plane loading[J]. Composites Science and Technology, 2010, 70:1042-1048.

[11] SPADONI A, RUZZENE M. Elasto-static micropolar behavior of a chiral auxetic lattice[J]. Journal of the Mechanics and Physics of Solids, 2012, 60(1):156-171.

[12] DOS REIS F, GANGHOFFER J F. Equivalent mechanical properties of auxetic lattices from discrete homogenization[J]. Computational Materials Science, 2012, 51:314-321.

[13] RUAN D, LU G, WANG B, et al. In-plane dynamic crushing of honeycombs A finite element study[J].International Journal of Impact Engineering, 2003, 28(2):161-182.

[14] LIU Y, ZHANG X C. The influence of cell micro-topology on the in-plane dynamic crushing of honeycombs[J]. International Journal of Impact Engineering, 2009, 36:98-109.

[15] 胡玲玲, 陈依骊. 三角形蜂窝在面内冲击荷载下的力学性能[J]. 振动与冲击, 2011, 30(5):226-230.

HU Lingling, CHEN Yili. Mechanical properties of triangular honeycombs under in-plane impact loading[J]. Journal of Vibration and Shock, 2011, 30(5):226-230.

In-planedynamiccrushingofchiralandanti-chiralhoneycombs

LUZixing，LIKang

(School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China)

The deformation modes and energy absorption properties of chiral and anti-chiral honeycombs with negative Poisson’s ratio under in-plane dynamic crushing were studied by means of numerical simulations. The results show that the deformation mode of the chiral family honeycombs at low impact velocities consists of two different stages: the first is the collapse of the ligaments and then is the collapse of the circular nodes. The deformation mode appears as the crushing of circular nodes and ligaments layer by layer at high velocities and a transitional mode with part features of both the low and high velocities modes at moderate velocities. The localized bands transit from the fixed end to the impact end as the impact velocity increases. When the velocity is low or moderate, the chiral family honeycombs display the dynamic auxetic responses. The results provide us a certain understanding of the dynamic behaviors and energy absorption properties of two-dimensional auxetic cellular materials and lay the foundation for understanding the impact behaviors of three-dimensional auxetic foam materials.

honeycomb; negative Poisson’s ratio; chiral; dynamic crushing; deformation mechanism

O347

A

10.13465/j.cnki.jvs.2017.21.003

国家自然科学基金(11472025)

2015-08-17 修改稿收到日期：2015-12-21

卢子兴 博士，教授，博士生导师,1960年9月生