滚珠自动控制转子系统强迫振动研究(1/2次分数谐波振动)
2017-11-30张小龙魏井福东亚斌何育民
张小龙, 魏井福, 东亚斌, 何育民
(西安建筑科技大学 机电工程学院,西安 710055)
滚珠自动控制转子系统强迫振动研究(1/2次分数谐波振动)
张小龙, 魏井福, 东亚斌, 何育民
(西安建筑科技大学 机电工程学院,西安 710055)
应用两个滚珠在线自动平衡转子系统,并控制转子系统的强迫振动。目前相关研究主要集中在线性转子系统,然而实际的转子系统大多属于非线性系统,特别是在常见的滚动轴承等支承的转子系统中,由于装配误差等原因出现弱非线性弹性恢复力。对具有弱非线性弹性恢复力作用的转子系统,在已完成的对主振动控制研究的基础上,通过理论解析与数值模拟,研究了两滚珠平衡制振时转子系统的1/2次分数谐波振动的响应特性及滚珠质量对振动响应大小的影响规律等。研究表明平衡滚珠在高速区域能够完全平衡非线性转子系统,对系统的1/2次分数谐波振动具有良好的制振性能。
非线性转子系统;滚珠平衡;1/2次分数谐波振动;振动控制
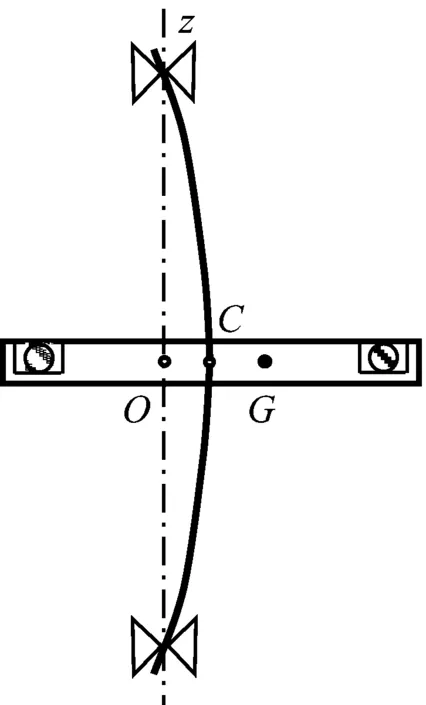
为了使不平衡的大小和方位随机变化的高速转子在运转中能够自动平衡,抑制转子系统发生的强迫振动,Tharle[1]提出了滚珠自动平衡转子的方案,其原理如图1所示。该制振方案结构简单、成本低,其原理已在光盘驱动器[2]、洗衣机[3]及汽车车轮[4]等一些滚动轴承支承的旋转机械的制振中获得了初步应用。
(a)
关于滚珠自动平衡转子系统的原理,已有许多理论与实验研究。井上等[5]用平均法研究了自动平衡的基本特性。太田等[6]求解出了转子系统的响应曲线,并进行了实验验证。这些研究基本上搞清楚了滚珠自动平衡转子系统并抑制其强迫振动的基本原理。在此基础上,近几年来主要进行了如何提高自动平衡性能的研究,例如Inoue等[7-8]研究了系统参数对主共振点附近发生的自激振动的影响,Ishida等[9-12]研究了如何降低摩擦力和残余不平衡的影响以提高自动平衡精度等问题。
(b)
以上研究中基本采用线性转子模型,加入平衡滚珠后系统的运动方程式变成非线性方程式。由于滚动轴承的角度间隙和滑动轴承的油膜特性等原因,使得轴的弹性恢复力具有非线性特性[13],转子系统发生各种非线性强迫振动。因此有必要研究自动平衡滚珠对非线性转子系统的平衡和制振性能。
非线性转子系统在转速与固有频率满足一定关系的转速附近发生相应的非线性强迫振动。对非线性转子系统的研究表明,在转速高于主共振转速的高速回转区域,较大的两个平衡滚珠可以自动平衡转子系统,并完全控制转子系统的主振动响应[14-16]。而在同时涉及控制转子系统分数谐波振动的研究中[15],为了研究主振动时使主共振点附近的多个共振频率发生分离,人为地在运动方程式中加入了陀螺力矩的影响,影响了研究结果的可靠性。
本文针对滚动轴承支承的具有弱非线性弹性恢复力的Jeffcott转子系统,研究自动平衡滚珠对转子系统分数谐波振动的制振特性等问题。
1 运动方程式和固有频率线图
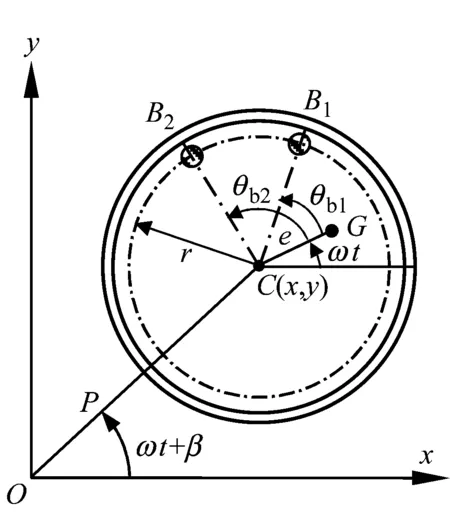
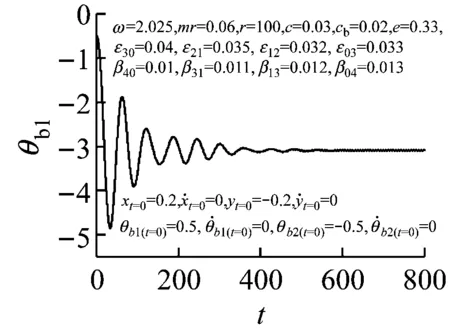
在如图1所示的Jeffcott转子系统中,设上下轴承中心连线为z轴、在圆盘回转平面内的o-xyz为固定坐标系、轴和圆盘交点C的弹性变形分别为x与y,C点轴的刚度为k、轴的旋转角速度为ω。
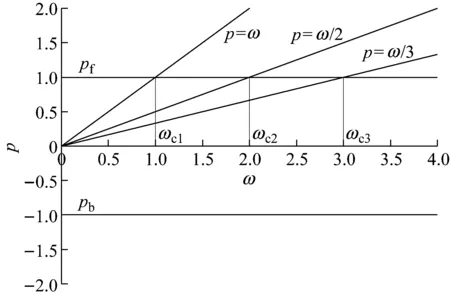
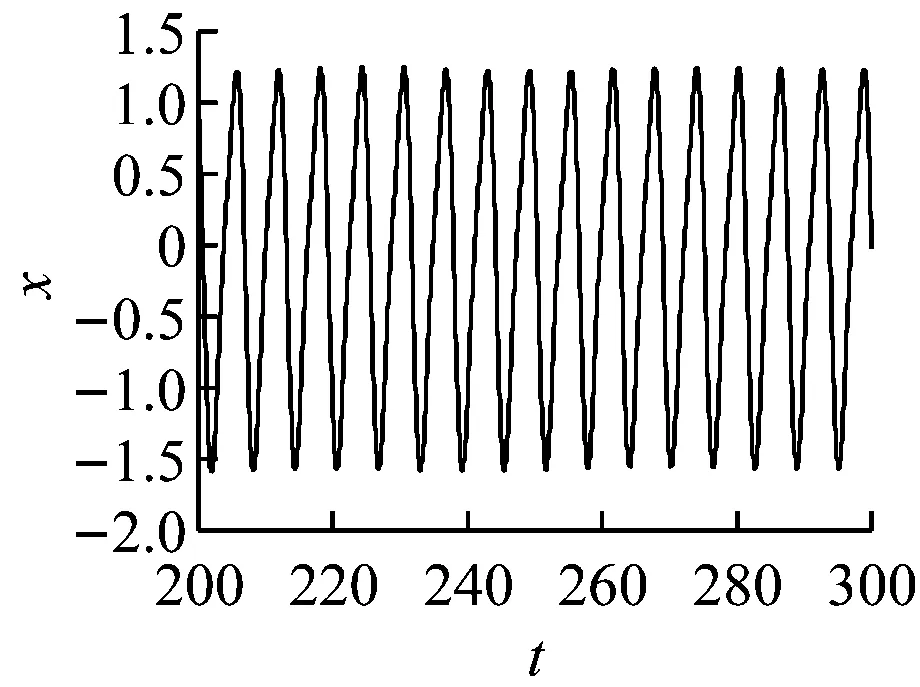
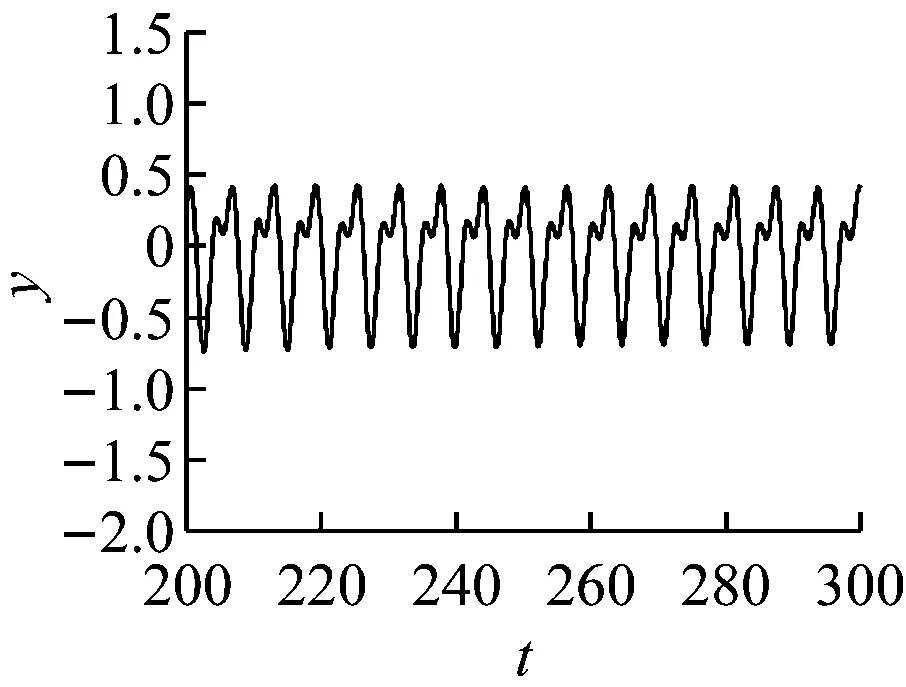
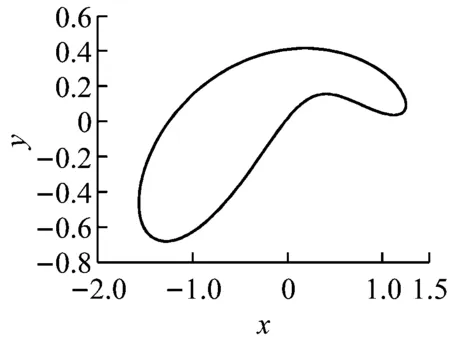
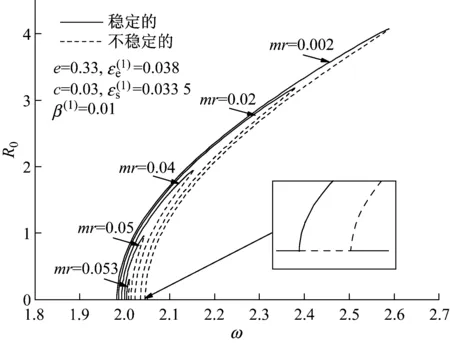
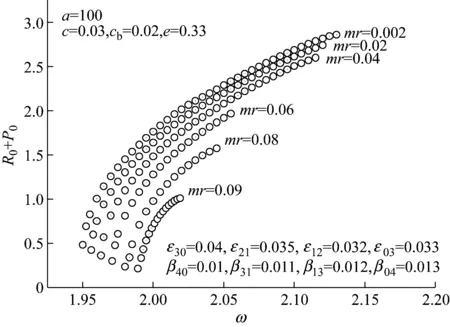
设圆盘的重心在G点、质量为M、静不平衡为e、运动的黏性阻尼系数为c。选择CG与x轴平行的瞬时时间t=0。在圆盘中放入两个平衡滚珠B1和B2,设滚珠的质量均为m(m< (1) 根据Lagrange运动方程式,系统的无量纲运动方程式为[15-16](为简化已省略了所有无量纲量的上标*): (2) 假设式(2)中无量纲的Nx、Ny、c、cb和乘积mr与微小量ε同等程度大小(以下用符号O(ε)表示)。无量纲的非线性项Nx、Ny的一般表达式为[13]: (3) 式中:εij称为非对称非线性项的系数;βij称为对称非线性项的系数;εij和βij的大小均为O(ε)。 考虑式(2)对应的自由振动,且略去阻尼力和其它O(ε)大小的量时,式(2)对应的关于系统固有频率p的频率方程式为1-p2=0,根pf=1和pb=-1分别为正向和反向进动的固有频率,如图2所示。图中在轴回转角速度ω与固有频率pf满足关系式pf=ω的转速ωc1=1.0附近系统发生主共振。如果非线性恢复力主要表现为非对称非线性,则在ω与pf满足式2pf=ω的转速ωc2=2.0附近系统会开始发生1/2次分数谐波振动。同理,如果非线性恢复力表现为对称非线性,则在ωc3=3.0附近会开始发生1/3次分数谐波振动。本文仅研究当式(3)中的非对称非线性项的系数相对较大时,系统发生的1/2次分数谐波振动及其控制问题。 图2 固有角频率线图 根据文献[16]关于转子系统主共振响应的研究结果,在转子转速大于主共振转速ωc1的高速区域,当2mr 为了方便振动解析,利用Matlab软件先对式(2)进行数值模拟,在2mr (a) 滚珠角位移θb1 (b) 滚珠角位移θb2 (c) 转子位移x (d) 转子位移y (e) 转子运动轨迹 (f) 转子振动FFT解析 而当2mr>e时,同样是ω=2.025点,数值模拟结果如图4所示。可以看出,此时两个滚珠分离,对称停留在圆盘重心相反方向的两侧,转子的振动响应收敛为零,转子系统完全得到平衡。 2.12mr (a) 滚珠角位移θb1 当2mr (b) 滚珠角位移θb2 (c) 转子位移x (d) 转子位移y (4) 式中,θf=ωt/2+δ。关于式中振动角频率为ω的主振动成分,此时作为已知量,其振幅P和相位角β为[16]: (5) 式中,β(0)=(3β40+β22+3β04)/8。 为了求解1/2次分数谐波振动响应,设式(4)中振幅R,a,b及δ是随时间缓慢变化的量,其大小为量级O(ε0)。将式(4)代入式(2)的前两式,使方程式两边cosθf和sinθf的系数按照O(ε)的精度相等,得以下4个表达式: 对以上四式进行加减运算,得: (6) 将式(4)代入式(2)的第三式,按照O(ε)精度使两边频率为零的项相等,得: (7) (8) 为了判别上述定常解的稳定性,对于振幅不等于零的定常解R0,δ0,θbi0(i=1,2),考虑O(ε)量级的微小扰动ξ,η,ζi(i=1,2),可按照文献[15]步骤并根据Routh-Hurwitz定理进行判别。对于振幅等于零的解,相位角δ0不确定,所以不能利用式(6)和(7)进行稳定性判别,这时对式(6)和(7)进行变换,令u=Rcosδ,v=Rsinδ,将式(6)和(7)的变量变换成u,v,同样可进行稳定性判别。定常解的幅频曲线及其稳定性如图5所示。可以看出,在R0≠0的定常解曲线与ω轴的两个交点之间的区间,解R0=0不稳定。而且随着平衡滚珠mr值或滚珠质量m的增加,R0≠0的曲线逐渐减小,当2mr大于e值时,R0=0的不稳定区间将消失,使定常解R0全部稳定为零。 2.22mr>e时的定常解及其稳定性 由于滚珠的自动平衡作用,当2mr>e时,根据文献[15],在ωc2转速附近仅存在P=0的稳定主振动响应,所以不论主振动响应还是1/2次分数谐波振动响应均为零。为了判定该1/2次分数谐波振动的稳定性,设O(ε)精度的解为: (9) 将式(9)代入运动方程式(2),根据谐波平衡法使方程式两边的系数相等,得到关于1/2次分数谐波振动的下述方程式: (10) 根据Routh-Hurwitz定理,稳定性判定的结果是振幅为零的1/2次分数谐波振动总是稳定的。 图5 1/2次分数谐波振动幅频曲线 Fig.5 Amplitude frequency curve of the 1/2 subharmonic vibration 利用Matlab软件数值模拟得到转子系统同时发生1/2次分数谐波振动和主振动时,mr值对转子径向响应最大值的影响规律如图6所示,mr值对转子振动轨迹的影响见图7所示。尽管数值模拟结果中同时包含1/2次分数谐波振动响应和主振动响应,但由于ωc2远大于ωc1,所以在ωc2转速附近的主振动响应较小,且响应的幅频特性曲线较平坦(参见式(5)),所以图6与图5定性基本一致。由图6、7可以看出,随着滚珠mr值的增大,转子发生1/2次分数谐波振动的区间和响应大小逐渐减小。在转子响应不为零时,两个滚珠总是接触在一起,同时处于回转体偏心的反方向一侧(参见图3)。当mr值增大到使2mr>e时,1/2次分数谐波振动和主振动都完全消失,两个滚珠的角位置准确地收敛于参考文献[16]的式(11),即θb10=cos-1(-e/(2mr))、θb20=-θb10,使转子系统达到完全平衡(参见图4)。如在图4(a)和(b)中,mr=0.17,e=0.33,由该式得到的理论值为θb10=166.069 4°,即θb10=2.898 46 rad,该理论值与图4的数值模拟结果相同。 图6 转子的最大径向位移 图7 转子的振动轨迹 对于具有非线性弹性的Jeffcott转子系统的分数谐波振动,本文通过理论解析和数值模拟,研究了加入自动平衡滚珠对振动的影响,主要结论如下: (1) 清楚了加入两个平衡滚珠的非线性Jeffcott转子系统的分数谐波振动响应的特性和规律。 (2) 在转子的高速回转区域,较大的两个平衡滚珠可以完全自动平衡转子系统,并控制转子系统的分数谐波振动,平衡滚珠可以用作自动平衡装置。 [1] THEARLE E L. A new type of dynamic balancing machine[J]. Transactions of the ASME, 1932, 54(12):131-141. [2] CHAN T C, SUNG C K, CHAO C P. Friction effect on ball positioning of an automatic balancer in optical disk drives [J]. Microsyst Technol, 2012, 18:1343-1351. [3] CHEN H W, ZHANG Q J, WU X Q. Stability and dynamic analyses of a horizontal axis washing machine with a ball balancer[J]. Mechanism and Machine Theory, 2015, 87:131-149. [4] MAJEWSKI T. The properties of a dynamic eliminator for vehicle vibrations[J]. Mechanism and Machine Theory, 2010, 45(10):1449-1461. [5] 井上順吉,末岡淳男.機械力学Ⅱ:非線形振動論[M].理工学社,2002. [6] 太田博,石田幸男,前田博雅,横井勝彦.自動バランサに関する基礎的研究[C]//日本機械学会全国大会論文集, 910-62(1991-10):29-32. [7] INOUE T, NIIMI H, ISHIDA Y. Vibration analysis of the self-excited vibration in the rotor system due to ball balancer[C].IDETC/CIE 2009. [8] INOUE T, ISHIDA Y, NIIMI H. Vibration analysis of a self-excited vibration in a rotor system caused by a ball balancer[J]. Journal of Vibration and Acoustics, 2012,134(2):021006. [9] ISHIDA Y, MATSUURA T, ZHANG X L. Efficiency Improvement of an Automatic Ball Balancer[J]. Journal of Vibration and Acoustics, 2012,134(2):021012. [10] ISHIDA Y. Recent development of the passive vibration control method[J]. Mechanical Systems and Signal Processing, 2012,29:2-18. [11] YOSHIDA S. Reduction Method of Residual Balancing Error in Auto-Balancer and its Motion Analysis[D]. Kyoto: Kyoto Institute of Technology, 2014. [12] SUNG C K, CHAN T C, CHAO C P, et al. Influence of external excitations on ball positioning of an automatic balancer[J]. Mechanism and Machine Theory,2013,68:115-126. [13] ISHIDA Y, YAMAMOTO T. Linear and nonlinear rotordynamics: A modern treatment with applications (2nd enlarged and improved edition)[M]. Wiley,2012. [14] CHAN T C, SUNG C K, CHAO C P. Non-linear suspension of an automatic ball balancer[J]. International Journal of Non-Linear Mechanics, 2011,46(2):415-424. [15] ISHIDA Y, ZHANG X L, LIU J, et al. Sup-pression of nonlinear resonances by an automatic ball balancer[C]. The Japan Society of Mechanical Engineers, Dynamics & Design Conference, 2008. [16] 张小龙,东亚斌,何育民.滚珠自动控制转子系统强迫振动研究(非线性主共振)[J].振动与冲击,2013,32(17):90-94. ZHANG Xiaolong, DONG Yabin, HE Yumin. Forced vibration of a rotor controlled by a automatic ball balancer[J]. Journal of Vibration and Shock, 2013, 32(17):90-94. Forcedvibrationoftherotorcontrolledbyanautomaticballbalancer(1/2ordersubharmonicvibration) ZHANGXiaolong,WEIJingfu,DONGYabin,HEYumin (School of Mechanical and Electrical Engineering of Xian University of Architecture and Technology, Shaanxi Xian, 710055, China) A rotor can be on-line balanced by using a balancer with two balls and its forced vibration can be suppressed well. Although, the rotor, especially supported by rolling elements bearings, often shows nonlinear character practically because of weakly elastic restoring forces caused by the assembly error, etc., the relevant researches are mainly focused on its linear ones. For the rotor acted by weakly nonlinear elastic restoring forces and balanced by two balls, based on the research results about the control of principal vibration, the 1/2 order subharmonic vibration response characters and the effect of the mass of balls on the vibration amplitude were studied theoretically and numerically. It is concluded that the balls can balance the nonlinear rotor completely and suppress the amplitude of 1/2 order subharmonic vibration response well in the high speed region. nonlinear rotor system; ball balancer; 1/2 subharmonic vibration; vibration control O347.6 A 10.13465/j.cnki.jvs.2017.21.004 国家自然科学基金(51175399);陕西省自然科学基础研究计划(2014JM7267) 2016-05-03 修改稿收到日期:2016-07-09 张小龙 男,博士,教授,博士生导师,1963年生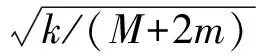
2 理论解析

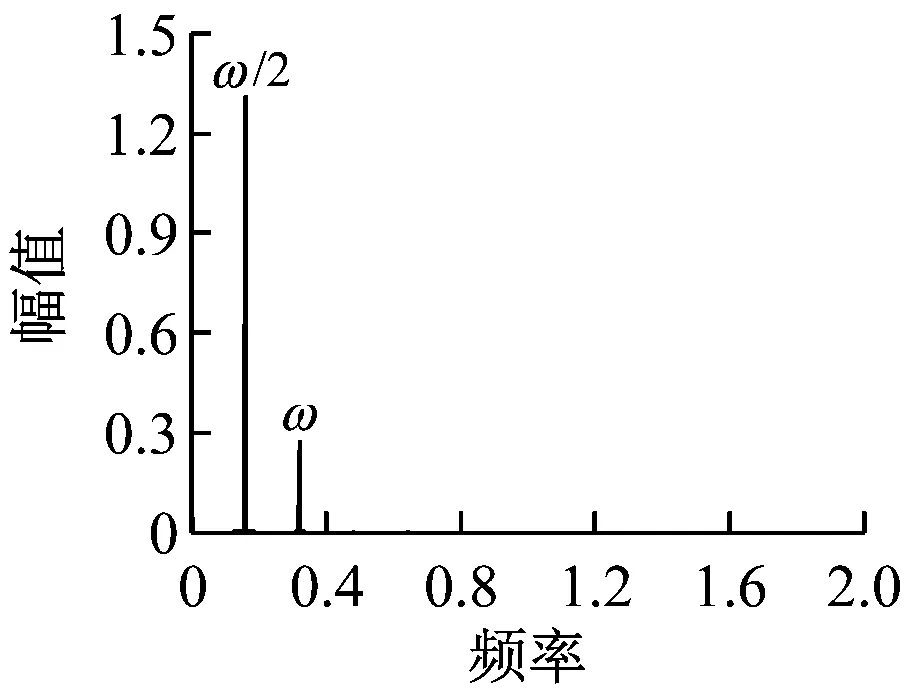
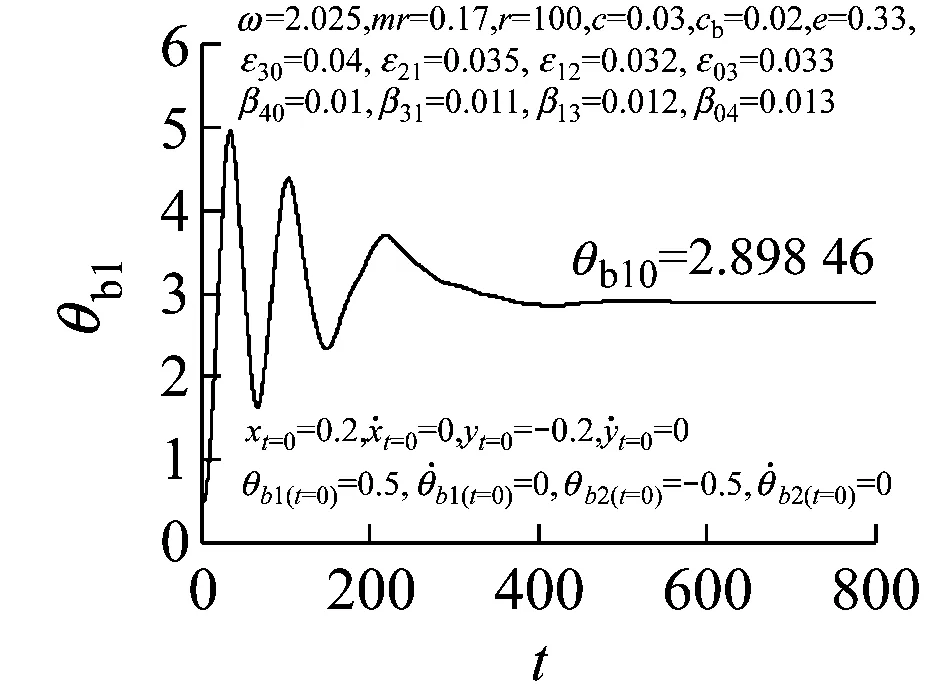
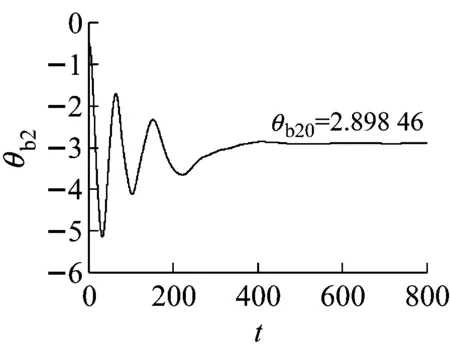


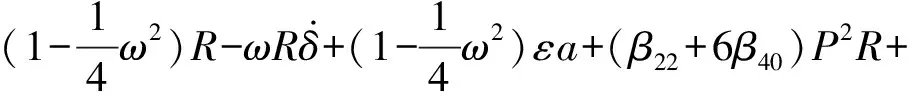
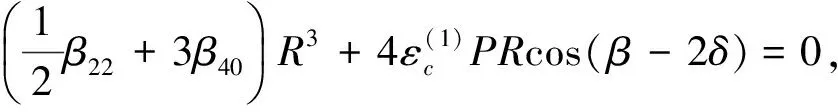
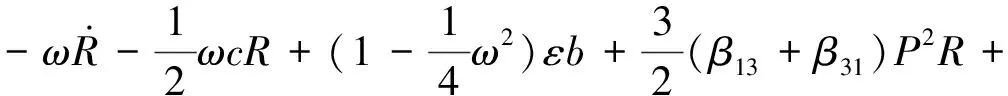
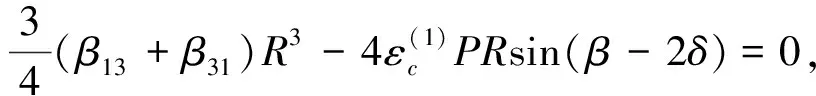
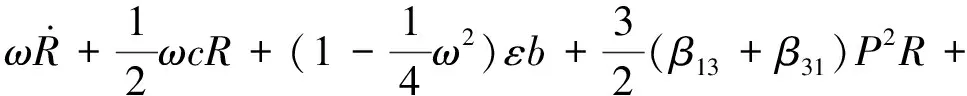
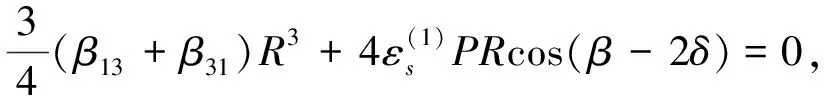
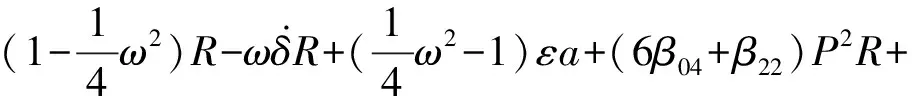

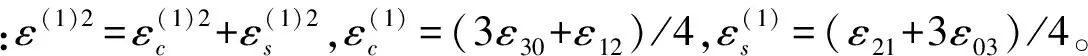
3 数值模拟

4 结 论
