基于自激励人体模型的人-结构竖向相互作用研究

谢伟平， 冯金鹏， 何 卫

(1.武汉理工大学 土木工程与建筑学院，武汉 430070; 2.武汉理工大学 理学院，武汉 430070)

基于自激励人体模型的人-结构竖向相互作用研究

谢伟平1， 冯金鹏1， 何 卫2

(1.武汉理工大学 土木工程与建筑学院，武汉 430070; 2.武汉理工大学 理学院，武汉 430070)

基于自激励人体模型，建立了考虑人-结构竖向相互作用下行人过桥运动方程，提出了考虑步频主谐和亚谐分量的单人步行力模型，并通过单人过桥试验对该模型进行了验证；分析了人-桥竖向相互作用的变化规律及影响因素。结果表明，人体步频亚谐可能与结构的基频相近，从而引起较大的结构响应；结构固有频率和人/结构质量比对人-结构相互作用影响较大，当结构频率与步频及其主谐波分量频率接近时，耦合效应最显著，其对人体足底力影响最大。随着人/结构质量比的增加，人-结构相互作用逐渐增强。

人致振动；竖向人体动力学模型；人-结构相互作用；足底力

随着经济的快速发展及高性能建筑材料的出现，造型独特、结构新颖的大跨度公用建筑大量涌现，如大跨人行天桥、大型车站、体育场馆等。这些大跨度结构大都具有自振频率低，人群密度大等特点，所以其人致振动响应问题引起了工程界和学术界的极大关注。这类结构的人致振动问题并不是简单意义上的强迫振动，而是由强迫振动引发的、包含人-结构动力相互作用的一种复杂的结构振动形式。然而，由于缺乏对人-结构相互作用效应深层次的认识，近年来学者们在分析此类结构的人致振动响应时多采用基于刚性测力平台实测的足底反力提出的傅里叶级数模型[1-3]进行求解，而该模型并未考虑人与结构间的相互作用对人体行走时足底反力的影响[4]，从而导致计算结果与实测值相偏离。因此，研究人-结构相互作用对分析结构的人致振动问题显得尤为重要，这一问题的解决将有助于提高人致振动计算理论的准确性和可靠性。

有研究表明当行人在刚度较小、基频较低的结构上行走时，产生的足底反力与在刚性测力平台上产生的足底反力相比有所变化[5]。Ohlsson[6]测得大跨轻型楼板上的竖向步行力不同于在刚性地面；Pimentel[7]研究发现实际人行桥测得的人行荷载动载因子不同于刚性地面的测试结果；Yao等[8]在研究人体跑步、跳跃荷载时发现在柔性结构上测得的人行荷载小于在刚性地面的数据。在国内，秦敬伟等[9]基于双足模型对考虑人-桥竖向耦合作用下的过桥过程进行了模拟，发现人体于柔性结构上行走时，产生的足底反力小于刚性地面时的结果。谢伟平等[10]就人-结构相互作用对人体行走时足底反力的影响做了初步的探索。综上所述，目前学界对于人-结构相互作用会影响人体行走时的足底反力这一结论已形成共识，但对于考虑耦合作用下足底反力的影响因素及变化规律的研究还有待开展。

本文采用单自由度人体模型，将人体简化为带有生物自激励的弹簧-质量-阻尼系统，建立考虑人-结构竖向耦合作用下行人过桥时的运动方程，提出了考虑步频主谐和亚谐分量的单人步行力模型，并通过在人行钢桥上进行试验实测，与模拟结果进行对比，从而验证模型的合理性与有效性。同时还进一步分析人/结构质量比和结构固有频率等因素对行人足底反力的影响，揭示人-桥相互作用的影响因素及变化规律。

1 人-结构竖向相互作用模型

1.1运动方程的建立

假设结构为等截面，即抗弯刚度EI为常数，线密度为mb，阻尼系数为c，梁上的外加激励是由人体行走而引起的，如图1所示。

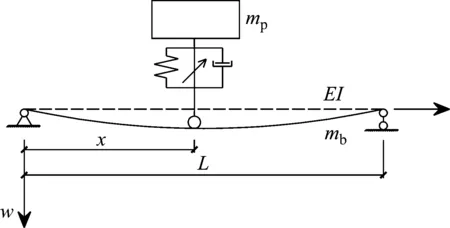
图1 人-结构相互作用模型

行人激励下，梁的运动方程表达式为[11]

(1)

式中：w为梁的挠度;Fp(x,t)为人对梁的作用力，表达式为

Fp(x,t)=fp(t)·δ(x-xp(t))

(2)

fp(t)为足底作用力时程，利用人体质心加速度表示如下

fp(t)=-mpg-mpac(t)

(3)

式中：mp为人体质量;ac(t)为人体质心加速度。梁振动时，人体的质心加速度分为两个部分：相对于结构运动产生的相对加速度acr(t)和随结构共同运动产生的牵连加速度ace(t)，即

ac(t)=acr(t)+ace(t)

(4)

ace(t)指人所处位置梁的振动加速度，可表示为

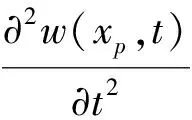
(5)

不考虑结构振动对人体行走步态的影响，则有

(6)

(7)

可见式(7)实质上将行人过桥时的作用力等效为刚性地面足底力与桥面振动引起的惯性力之和。利用振型叠加法求解式(7)，简支欧拉-伯努利梁振型函数为

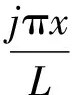
(8)

则有

φi(x)

(9)

将式(9)代入式(7)则有

(10)

将式(10)中的每一项乘以第j个振型函数φj(x)，并沿梁的全长进行积分，右端的结果为

(11)

则广义力为

(12)

将式(12)代入式(10)整理可得

(13)

则有

(14)

这是一个无穷多自由度的联立方程组。如果位移级数取N项，则结构的广义自由度为N，系统的N阶矩阵表达式为

(15)

式中,广义位移向量U=[q1,q2,…,qN]T，广义的质量矩阵、阻尼矩阵、刚度矩阵以及力向量分别如式(16)～(19)所示。

(16)

(17)

(18)

F=[ρFφ1,ρFφ2,…ρFφN]T

(19)

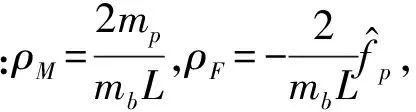
人体在结构上移动时，方程中的系数会不断变化，因此式(15)为时变系统的多阶微分方程组，应采用非线性的动力分析方法。本文基于Newmark-β法对上述方程进行求解。

1.2单人步行力模型的建立

(20)

2 荷载模型的验证

本文通过在一轻柔单跨人行钢桥上进行单人行走实验来验证模型的有效性。该人行桥全长10.5 m，有效长度10.3 m，两边简支，线密度为73.7 kg/m，经实测，该桥一阶竖弯频率为2.734 Hz。如图2所示。

图2 人行钢桥

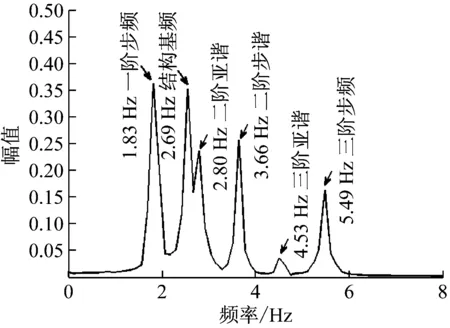
开展单人过桥试验时令体重为85 kg的行人在节拍器的提示下以不同步频通过人行桥，图3为步频为1.83 Hz时实测跨中加速度时程曲线和文中模拟结果对比，图4为两者的频谱对比。

(a) 实测结果

(b) 本文模拟结果

由图3可以看出，模拟结果与实测响应波形走势基本吻合。从频域上来说，两者的频率成分基本吻合，都可以明显的看出结构的一阶频率和人体的前三阶步频。实测频率成分相对更为丰富，包含了结构的高阶模态和人体的高阶步频成分。实测频谱在结构一阶频率处达到最大峰值，原因是人体行走步频的二阶亚谐(1.5fs)与该阶频率相近，从而导致此处响应较大。模拟频谱中步频二阶亚谐处也出现了一个峰值，原因同上。此外，实测结果的幅值略小于模拟结果，这是由于实测的频率成分更加丰富，能量分布更加分散。

(a) 实测结果

(b) 本文模拟结果

表1则给出了不同步频下跨中均方根加速度、峰值加速度的实测结果与模拟结果对比，从表中可以看出，模拟结果最大误差不超过10%，基本满足精度要求。

表1 不同步频下模拟与实测结果对比

通过上述分析可知，文中的人-桥竖向耦合系统的动力分析和求解程序基本正确，可用于研究人-桥竖向耦合系统的人致振动相关问题。

3 足底反力影响因素分析

目前在对人行桥进行振动分析时，选用的人体步行荷载多为傅里叶级数模型荷载或单步落足荷载，然而这些模型几乎都是基于固定地面或刚性结构上的测试结果提出来的，与实际存在差异。近年来随着柔性结构的逐渐增多，人们越来越认识到人与结构之间存在相互作用影响。有学者研究发现当人体在柔性结构上行走时的足底力与刚性地面所测得足底力有所不同，并且两者的差异与相互作用的大小有关。

为分析人-结构竖向相互作用对足底力的影响，将人体于柔性结构上行走时的足底力与刚性测力平台上所测足底力的差值进行无量纲化处理，定义相互作用力影响函数[13]

(21)

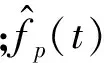
由式(10)可知，式(21)可表示为

(22)

即DI(t)为行人所在位置处结构加速度和重力加速度的比值。

3.1人/结构质量比对足底反力的影响

算例梁长9 m，宽0.8 m，高0.12 m，阻尼比0.003，基频为2 Hz，为研究人/结构质量比对足底反力的影响，令人/结构质量比为u，保持结构基频不变，令人体步频与结构基频相同，并通过对梁体的材料参数(密度和弹性模量)进行改变以实现不同的人/结构质量比。

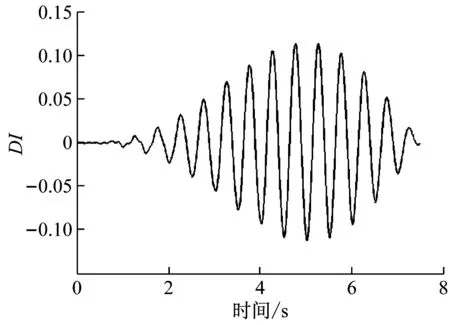
图5所示为不同人/结构质量比下无量纲相互作用力影响函数曲线。

相互作用力影响函数DI曲线反映了人运动位置处结构的加速度状况，由图5可以看出，当行人由梁端部向跨中行走时，DI逐渐增大，随着行人逐渐远离，DI逐渐减小直到行人离开结构。DI达到最大值的位置并不在结构的跨中，而是在其附近的某一位置，具体位置与人/结构质量比有关，原因是人体行走时人-桥耦合系统为一时变体系，结构的振型迹线在不断发生变化；当人/结构质量比较小时，人/结构相互作用随着质量比的增加逐渐增强，相互作用力影响系数逐渐增大，但是当质量比增大到一定程度时，人-结构相互作用力反而减小，原因是较大的质量比使此时结构的自振频率发生了改变，导致激振频率远离了结构的自振频率。

(a) u=0.01

(b) u=0.05

(c) u=0.1

Fig.5 The interaction force time-history curve of different human/structure mass ratio

3.2结构频率对足底反力的影响

算例保持3.1节算例中梁的截面参数及阻尼特性不变，线密度为230.4 kg/m，梁1杨氏模量E=30 GPa，基频f=2.375 Hz；梁2杨氏模量E=14.5 GPa，基频f=1.65 Hz。人体质量80 kg，步频取2 Hz。

图6所示为人体分别在梁1和梁2上行走时的归一化足底反力(足底力/人体体重)时程图，通过图中可以看出，人体在柔性结构上行走时的足底反力与刚性地面的有所不同，随着人体向跨中移动，足底反力增大或减小，具体变化规律与结构频率有关。考虑到人/结构质量比很小，为3.7%，因此可以认为：当结构刚度较小，基频较低时，人与结构件的相互作用较为显著，结构振动对人行荷载产生的影响也较为明显。

为进一步研究结构频率对足底反力的影响，定义DI的幅值为相互作用力影响系数，记为DF

DF=DI(t)max

(a) 梁1(f=2.375 Hz)

(b) 梁2(f=1.65 Hz)

(23)

图7为不同人/结构质量比时相互作用力影响系数DF与结构频率的关系曲线。

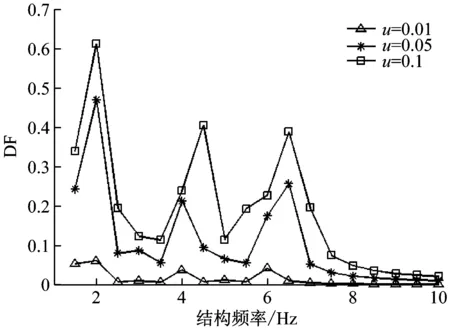
图7 相互作用力影响系数与结构频率的关系

Fig.7 The relationship between the influence coefficient of the interaction force and the frequency of the structure

由图7可知，当结构频率与激振频率(2 Hz)及其某阶主谐波频率相近时，人-结构耦合效应十分显著，此时行人足底反力与刚性地面相比有显著变化，而随着结构频率的增大，相互作用力影响系数下降较快且趋于平缓。当结构频率大于8 Hz时，人-结构相互作用已经很弱，表明行人足底力与在刚性地面行走时差别很小，此时在人/结构质量比较小的情况下可以不考虑人-结构相互作用的影响，而将行人动荷载作为外激励；随着人/结构质量比的增加，相互作用力影响系数逐渐增大，这主要是由于人体参振质量增大从而使人-结构相互作用逐渐增强。因此对于大跨度轻质、柔性结构(如大跨人行桥等)，当结构上人员密度较大时，需考虑人-结构相互作用的影响。

4 结 论

本文基于自激励弹簧-质量-阻尼模型，建立了人-结构相互作用系统的运动方程，与实测对比验证了模型有效性后，进行了数值分析，结果表明：

(1)人体于结构上行走时，步频亚谐(0.5fs，1.5fs，2.5fs)可能与结构的基频相近，从而引起较大的结构响应。

(2)结构固有频率和人/结构质量比对人-结构相互作用有较大影响。当结构频率与步频及其主谐波分量频率接近时，耦合效应最显著，其对人体足底反力影响最大。结构频率越大，人-结构相互作用就越弱，此时对于人/结构质量比较小的情况，可将结构上的人行荷载视为外激励。随着人/结构质量比的增加，相互作用力系数逐渐增大，人-结构相互作用逐渐增强。因此对于大跨度轻质柔性结构在人员密度较大时，需考虑人-结构相互作用的影响。

[1] 陈隽, 王浩祺, 彭怡欣. 行走激励的傅里叶级数模型及其参数的实验研究[J]. 振动与冲击, 2014, 33(8):11-15.

CHEN Jun, WANG Haoqi, PENG Yixin. Experimental investigation on fourier-series model of walking load and its coefficients [J]. Journal of Vibration and Shock, 2014, 33(8): 11-15.

[2] 李爱群, 陈鑫, 张志强. 大跨楼盖结构减振设计与分析[J]. 建筑结构学报, 2010, 31(6):160-170.

LI Aiqun, CHEN Xin, ZHANG Zhiqiang. Design and analysis on vibration control of long-span floor structures [J]. Journal of Building Structures, 2010, 31(6):160-170.

[3] 聂建国, 陈宇, 樊健生. 步行荷载作用下单跨人行桥振动的均方根加速度反应谱法[J]. 土木工程学报, 2010, 43(9): 109-116.

NIE Jianguo, CHEN Yu, FAN Jiansheng. RMS acceleration response spectrum method for single-span footbridges under pedestrian load [J]. China Civil Engineering Journal, 2010, 43(9):109-116.

[4] 袁旭斌. 人行桥人致振动特性研究[D]. 上海: 同济大学, 2006.

[5] 李红利, 陈政清. 人-桥竖向动力相互作用响应理论与试验研究[J]. 土木工程学报, 2014, 47(6):78-87.

LI Hongli, CHEN Zhengqing. Analytical and experimental study on vertically dynamic interaction between human and bridge [J]. China Civil Engineering Journal, 2014, 47(6):78-87.

[6] OHISSON S. Floor vibration and human discomfort [D]. Gortborg: Chalmers University of Technology, 1982.

[7] PIMENTEL R L. Vibrational performance of pedestrian bridges due to human-induced loads [D]. Sheffield: University of Sheffield, 1997.

[8] YAO S, WRIGHT J R, PAVIC A, et al. Forces generated when bouncing or jumping on a flexible structure [C].Proceedings of the International Conference on Noise and Vibration, 2002, 2: 563-572.

[9] 秦敬伟, 杨庆山. 基于双足步行模型和反馈机制的人体-结构相互作用[J]. 建筑结构学报, 2014, 35(增刊1):18-24.

QIN Jingwei, YANG Qingshan. Human-structure interaction based on bipedal walking model and feedback mechanism [J]. Journal of Building Structures, 2014, 35(Sup1):18-24.

[10] 谢伟平, 鲁伟, 何卫. 人-板耦合系统动力响及相互作用研究[J]. 武汉理工大学学报, 2013, 37(1):56-62.

XIE Weiping, LU Wei, HE Wei. Research on dynamic response and interaction of human-floor coupled system [J]. Journal of Wuhan University of Technology, 2013, 37(1):56-62.

[11] 刘隆. 人群与梁的竖向相互作用及人行桥侧向振动机理研究[D]. 武汉: 武汉理工大学, 2013.

[13] 何卫. 大跨度高铁车站振动舒适度理论与试验研究[D]. 武汉: 武汉理工大学, 2014.

Verticalhuman-structureinteractionbasedonaself-excitinghumanmodel

XIEWeiping1,FENGJinpeng1,HEWei2

(1. School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan 430070, China; 2. School of Science, Wuhan University of Technology, Wuhan 430070, China)

Based on a self-exciting human model, the motion equation of a footbridge was established in considering the vertical human-structure interaction and a walk force model was proposed in considering the main harmonic and subharmonic frequencies of walking. The model was verified by measuring the footbridge vibration responses caused by single person walking. The variation of vertical human-structure interaction and its influencing factors were analyzed. The results indicate that the walking subharmonic frequency may be close to the fundamental frequency of the structure, resulting in large structural responses. The natural frequency of the structure and the human/structure mass ratio have a great influence on the human-structure interaction. When the structural frequency is closer to the walking frequency or its main harmonic components, the coupling effect is significant and has the greatest impact on footfall forces. Moreover, with the increasing of human/structure mass ratio, the interaction will strengthen gradually.

human-induced vibration; vertical human dynamic model; human-structure interaction; footfall force

TU311.3

A

10.13465/j.cnki.jvs.2017.21.005

国家自然科学基金(51508431);中国博士后科学基金(2015M582288)

2016-02-02 修改稿收到日期：2016-06-15

谢伟平 男，博士，教授，1965年6月