基于易损性的高墩多塔斜拉桥纵向减震控制研究

胡思聪 ， 李立峰,2， 王连华,2

(1. 湖南大学 土木工程学院， 长沙 410082； 2. 湖南大学 风工程与桥梁工程湖南省重点实验室， 长沙 410082)

基于易损性的高墩多塔斜拉桥纵向减震控制研究

胡思聪1， 李立峰1,2， 王连华1,2

(1. 湖南大学 土木工程学院， 长沙 410082； 2. 湖南大学 风工程与桥梁工程湖南省重点实验室， 长沙 410082)

为研究常用的减震控制方式在高墩多塔斜拉桥这种新型结构中的减震效果，以一座墩高178 m的斜拉桥为例，建立了非线性有限元动力分析模型。从PEER强震数据库中选取80 条实测地震波进行非线性时程分析；结合结构的特点，定义各关键构件的损伤指标；基于易损性分析理论，建立了关键构件及桥梁系统的易损性曲线；以铅芯橡胶支座和黏滞阻尼器为代表，通过易损性曲线对比研究了不同控制参数和布置形式下，位移型及速度型两类减震控制方式的减震效果；结合桥梁实际情况确定最优的减震方案。分析结果表明：由于高墩的影响，斜拉桥的支座系统、主梁和拉索的损伤概率显著增加，而索塔损伤相对轻微；由于传力机理的差异，不同布置形式下控制参数对减震效果的影响规律不同；无论是位移型还是速度型控制方式，梁端布置形式的减震效果均优于塔梁布置形式；对于相同的布置形式，速度型控制方式较位移型控制方式效果更加显著。

桥梁工程；多塔斜拉桥；高墩；减震控制；易损性评估；铅芯橡胶支座；黏滞阻尼器

斜拉桥作为一种造型美观的桥型，在已建桥梁中占有很大比重。由于斜拉桥阻尼低、刚度小，在地震作用下往往容易产生较大的变形，引起构件或结构的损伤。因而，减震控制成为了斜拉桥设计中一个重要环节。一般来说，减震控制装置一方面能改变斜拉桥的刚度，调整地震能量的输入，改善结构惯性力的分布；另一方面能增大结构阻尼，增强结构的耗能能力。目前，许多学者纷纷开展了斜拉桥减震控制研究，并针对各类斜拉桥提出了不同的减震控制方案。总的来说，斜拉桥减震控制方式主要包括位移相关型控制、速度相关型控制两大类。李建中等[1]以铅芯橡胶支座为例，研究了位移型控制装置对斜拉桥纵向地震响应的控制效果；张锴等[2]采用正交设计法对斜拉桥中位移型控制装置进行参数优化设计；焦驰宇等[3]以弹性索为例，研究了位移型控制装置对斜拉桥的控制效果；叶爱君等[4]以黏滞阻尼器为例，研究了各控制参数对大跨斜拉桥减震效果的影响；刘彦辉等[5]研究了全漂浮大跨斜拉桥中速度型减震控制装置的布置原则；赵国栋等[6-7]对比研究了位移型控制和速度型控制对斜拉桥的减震控制效果，认为两种控制方式对不同的结构响应存在不同的减震效果，两类控制方式组合使用能获得最好的减震效果。

以上研究表明桥梁结构形式的差异，对减震控制装置的选择和参数的选取有重要影响，而过去研究大多针对于常规的低墩双塔斜拉桥。实际上，随着我国西部交通的快速发展，斜拉桥逐渐在山区公路中采用。为克服山区中的峡谷地形，斜拉桥可能会采用多塔、高墩的结构形式，如赤石特大桥[8]、神农溪大桥、铁罗坪特大桥、武陵山大桥等。国外的情况也是如此，如法国的Millau高架桥、墨西哥的Mezcala大桥等。高墩斜拉桥的纵向刚度较小，使得其动力特性与常规斜拉桥有所不同，高阶振型可能存在较大影响；高墩引起结构重心上升，可能加剧P-Delta效应的影响，自重等荷载对结构的地震响应存在较大影响；同时，塔梁质量比显著增大，改变了全桥惯性力分布，增加减震控制的难度；另外，桥墩与上塔柱高度比增加，改变了惯性力沿塔梁约束和锚固区传力的力臂长度比，可能导致其在抗震结构体系的选择上和常规斜拉桥不同。以上各种差异共同导致高墩斜拉桥与常规斜拉桥抗震性能可能存在较大不同，过去常用的减震控制方式，在这类新桥型中的适用性和有效性还有待进一步研究。

另一方面，过去的减震控制研究往往基于特定几条地震波的确定性分析，其结果非常依赖所选地震波的频谱特性，不能充分考虑地震运动的不确定性。同时，在减震效果评估时，往往面临着需要权衡多重指标(如主梁位移、桥墩弯矩、拉索索力等)的问题，难以准确选择真正意义上的合理减震措施。相比之下，采用基于概率的易损性评估方法[9-11]研究斜拉桥抗震性能，从基于性能的角度评估减震控制效果的优劣，能较好解决传统方法的局限。

基于此，本文以国内一座典型的高墩多塔斜拉桥为工程背景，结合易损性分析理论，对两类控制方式，在不同布置形式和设计参数下的减震效果进行研究，最终确定最优的减震控制方案。

1 工程背景

本文算例为一座四塔预应力混凝土双索面斜拉桥。斜拉桥跨径布置165 m+3×380 m+165 m，桥梁全长1 470 m。桥梁总体布置如图1(a)所示。主梁采用C55混凝土，截面为单箱四室截面(见图1(b))，梁高3.2 m，梁顶宽27.5 m，梁底宽16.14 m；索塔结合了A型塔和双肢薄壁墩的特点，采用了“纤腰”且“镂空”的双曲线外形，如图1(c)所示。索塔采用C50混凝土，根据不同截面形式可划分为上塔柱、中塔柱、下塔柱三个部分(见图1(d))，桥面以上的部分为上塔柱，高度为103.9 m，采用空心八边形截面(SecA, SecB)；中塔柱及下塔柱总高度为150.07～177.7 m，采用带凹槽的收腰形薄壁截面(SecC, SecD)；每个索塔布置46对斜拉索；5#索塔采用扩大基础，6#～8#索塔采用群桩基础；斜拉桥采用混合约束体系，其中6#索塔和7#索塔与主梁固结，5#索塔和8#索塔与主梁之间采用半漂浮形式；梁端伸缩缝采用960型RB多向伸缩装置。

图1 桥梁总体布置及构造形式(单位：cm)Fig.1 Elevation view and structural forms of bridge (unit: cm)

2 模型建立及地震波选择

2.1 模型建立

采用OpenSees建立斜拉桥有限元分析模型，如图2所示。其中主梁及索塔均采用非线性梁单元模拟。拉索采用桁架单元模拟；为反映拉索松弛和屈服行为，拉索采用理想弹塑性材料；拉索弹性模量按照Ernst公式折减以考虑拉索垂度效应。拉索与主梁、索塔之间均采用刚性连接。采用带有间隙的弹性单元模拟梁端碰撞；过渡墩采用弹性梁单元模拟。索塔塔底通过6个弹簧单元模拟桩-土相互作用。6#和7#索塔与主梁设置刚性连接，5#和8#索塔与主梁耦合竖向位移。我国桥梁抗震设计规范建议，斜拉桥的阻尼比应≤0.03，考虑到本文斜拉桥为混凝土结构，故本文将阻尼比取为建议值的上限0.03。为考虑恒载对结构地震响应的影响，时程分析前进行非线性静力分析，分析过程中考虑梁柱效应的几何非线性。

动力分析表明：结构一阶振型为纵向振动，周期为6.66 s。

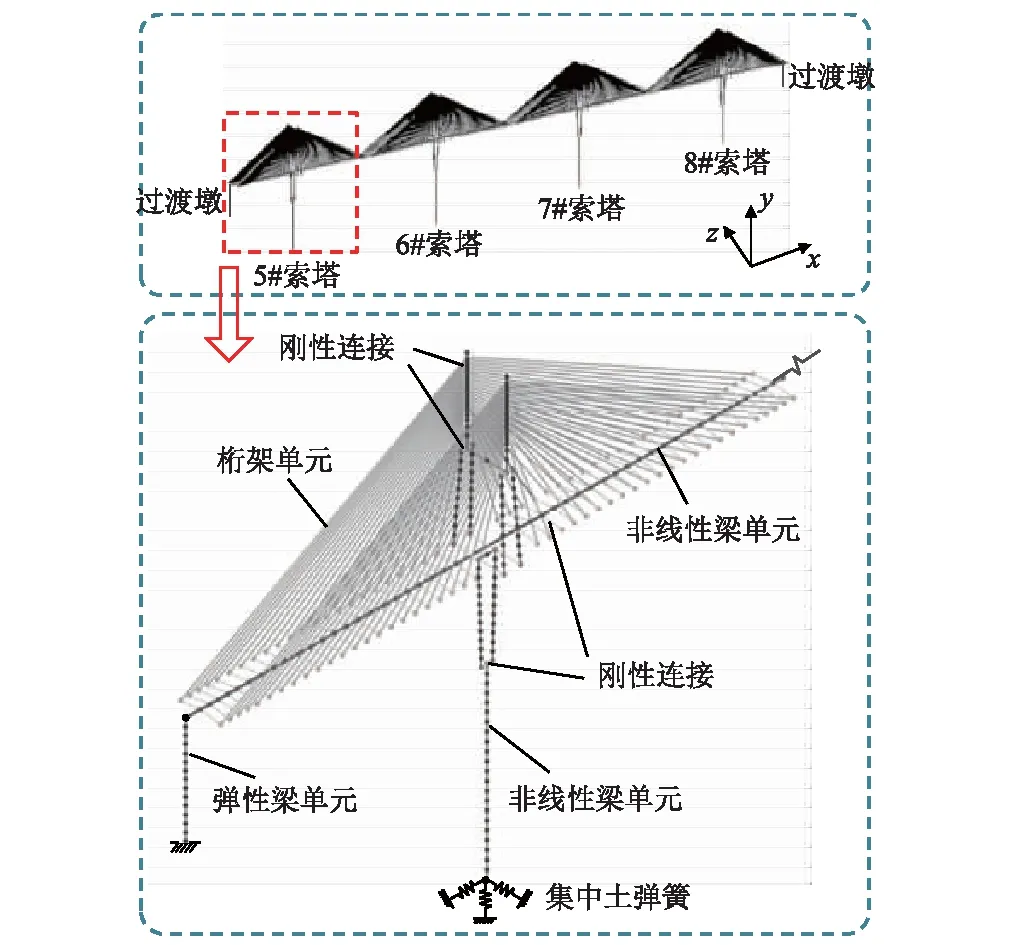
图2 有限元模型示意图Fig.2 The finite element model of structure

2.2 地震波选择

本文从美国太平洋地震工程研究中心强震数据库中选择了80 条实测地震波进行非线性时程分析。为充分考虑地震波的随机性，所选地震波特性参数涵盖较广的范围。其中震级为5.9～7.6，PGA为0.06～1.23g，PGV为16～187 cm/s，PGD为7～324 cm。由于本文主要研究的是斜拉桥纵向地震响应，因而地震波采用纵向单一方向输入。桥梁位于较为均匀的基岩层，行波效应的影响有限，因此本文分析时暂不考虑行波效应影响，地震波采用各点一致输入方式。所选地震波的加速度谱和位移谱，如图3所示。

图3 所选地震波的加速度谱及位移谱Fig.3 The acceleration spectrum and displacement spectrum of selected ground motions

3 斜拉桥减震控制措施

为避免强震作用下，斜拉桥产生过大的损伤，往往需要设置减震控制装置来改善结构抗震性能。目前，实际运用到斜拉桥的减震控制措施多为被动控制措施。FEMA274[12]将被动控制划分为位移相关型装置、速度相关型装置。以下针对这两类控制方式分别进行介绍。

3.1 位移型控制方式

位移型控制装置的耗能大小取决于控制装置自身的变形或相对滑动位移。当相对位移达到预定值时，控制装置发挥耗能作用。桥梁中常用的位移型控制方式有铅芯橡胶支座、摩擦摆支座、金属阻尼器等。本文以常见的铅芯橡胶支座为代表进行研究。

铅芯橡胶支座由传统的橡胶支座和内置的铅芯组成，通过铅芯屈服后的滞回特性起到耗能的效果。铅芯橡胶支座的滞回关系可近似采用双折线模拟，如图4(a)所示。在铅芯屈服之前，支座整体刚度K1由橡胶支座和铅芯共同提供；当支座水平力超过铅芯屈服荷载Fy后，铅芯发生屈服，支座整体刚度主要K2由橡胶支座提供。

3.2 速度型控制方式

速度型控制装置的耗能取决于加载频率或加载速度。黏滞阻尼器是最常见的速度型控制。黏滞阻尼器目前多采用Maxwell阻尼模型模拟，它由一个弹簧和非线性阻尼器串联而成。阻尼力与速度的关系可表达为

(1)

图4 两类减震控制方式的滞回模型示意图Fig.4 The hysteretic model of seismic control devices

3.3 布置形式及控制参数

一般来说，减震控制装置的减震效果取决于装置的布置形式及控制参数。根据上述控制方式的描述可知，屈服荷载和阻尼系数分别是决定铅芯橡胶支座和黏滞阻尼器耗能能力的最重要因素，因而本文重点研究这两个参数对减震效果的影响。在分析过程中，铅芯橡胶支座的屈服位移结合实际支座高度和铅芯屈服应变取为0.03 m，支座刚度比K1/K2参照文献[13]取为6.5；黏滞阻尼器的速度指数α=0.3。另一方面，对于多塔斜拉桥而言，为提高结构刚度，同时避免较大的温度次内力，可能会采用中塔固结边塔漂浮的结构体系。因而，控制装置可以选择布置在边塔塔梁之间或主梁端部。本文针对铅芯橡胶支座和黏滞阻尼器两类控制方式，分别考虑以上两种布置形式。其中梁端布置形式，在主梁两端各设置2个大直径铅芯橡胶支座或2个黏滞阻尼器；塔梁布置形式，在两个边塔塔梁连接处各布置4个大直径铅芯橡胶支座或4个黏滞阻尼器。综上所述，各控制参数取值如表1所示。

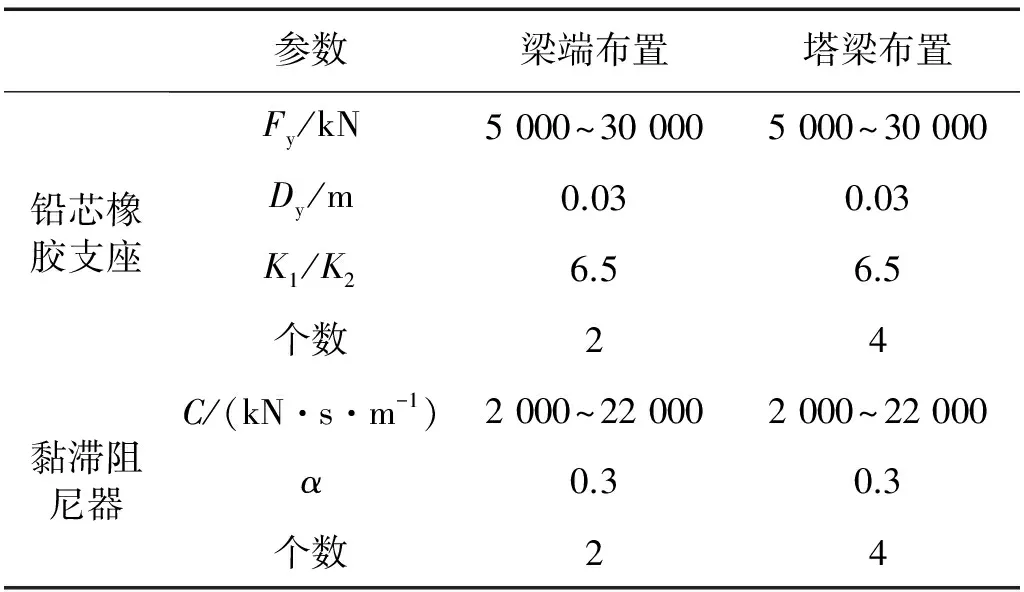
表1 控制参数取值

4 易损性分析理论

4.1 易损性理论概述

易损性曲线描述了地震作用下,构件的地震需求达到或超过规定损伤极限状态的概率。目前，常用两参数对数正态累积分布函数来表示地震易损性曲线

(2)

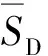
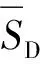
(3)

式中，a,b分别为相应的估计参数，可以通过最小二乘回归分析得到。为了计算的方便，常对上式进行对数转换得到如下的线性回归函数

(4)

此时，式(2)中的对数标准差βD可以按照式(5)进行计算

(5)

式中：SDi为第i条地震波下构件的工程需求参数；N为地震波的数量。结合概率需求模型及损伤模型，根据式(2)可以计算特定IM下的失效概率。将不同IM下的失效概率连线，便可以最终建立易损性曲线。

4.2 损伤模型

如上所述，定义各构件的损伤模型是建立易损性曲线的关键环节。目前，桥梁可根据其健康状态划分为无损伤、轻微损伤、中等损伤、严重损伤和完全损伤5个不同的等级[16]。考虑到大型斜拉桥发生完全损伤的概率非常低，而实际工程也不能接受此类结构完全损伤。因此，本文仅研究轻微损伤、中等损伤、严重损伤三种状态。借鉴过去梁桥损伤指标选取原则[17-18]，结合斜拉桥自身特点，本文定义了索塔、主梁、斜拉索、支座系统四类关键构件的损伤指标，下面针对损伤指标的定义进行说明。

斜拉桥的索塔与梁桥桥墩一样主要承担轴力和弯矩，因而可以采用相同的损伤指标。在既往的研究中，用来量化钢筋混凝土墩柱地震损伤的指标有很多。为考虑高阶阵型的影响，同时兼顾指标的简便性，本文选用曲率延性比μθ=φ/φy作为索塔的损伤指标。根据截面的弯矩-曲率关系，将钢筋首次屈服、截面出现塑性铰，截面达到最大弯矩能力对应的曲率延性比作为索塔的3个损伤状态(见图5(a))。

主梁和索塔一样均为压弯构件。因此，本文采用与索塔相同的定义方法，将曲率延性比作为主梁的损伤指标，并同样定义3个损伤状态，如图5(a)所示。

拉索作为斜拉桥重要的传力构件，在强震作用下也可能发生损伤。本文定义应变比αC=ε/εg来描述拉索的损伤状态，如图5(b)所示。其中ε和εg分别为地震荷载作用下和恒载作用下拉索轴向应变。通常来说，拉索张拉力大约控制在极限承载力的40%左右[19]，当αC=2.50时拉索达到极限承载力，对应为严重损伤状态；当αC=2.00时地震荷载下索力增加一倍，将其定义为轻微损伤状态；另将αC=2.25定义中等损伤状态。

支座系统的损伤主要考虑主梁位移是否超过其设计限值，从而导致结构损伤或产生落梁。本文采用主梁梁端纵向位移dG作为损伤指标，如图5(c)所示。并根据结构实际尺寸，确定了三种损伤状态：①轻微损伤，梁端位移达到伸缩缝设计容许位移，可能引起主梁碰撞。②中等损伤，主梁位移尺寸超过支座尺寸，造成主梁滑落支座。③严重损伤，梁端位移超过盖梁尺寸，可能引起落梁破坏。

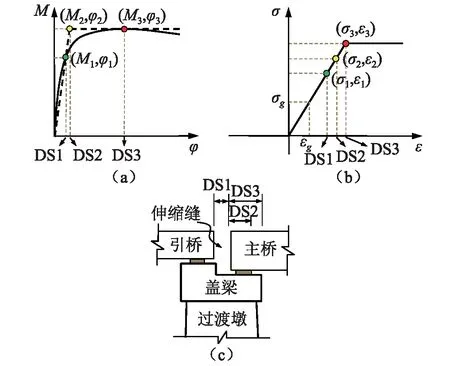
图5 构件损伤状态示意Fig.5 Component damage limit states

根据以上的确定方法，结合结构的实际尺寸，可以计算得到各构件不同损伤状态下的损伤指标，如表2所示。其中根据最不利原则，斜拉索选择92#拉索；主梁选择701 m处截面；索塔选择收腰处截面(SecD)。

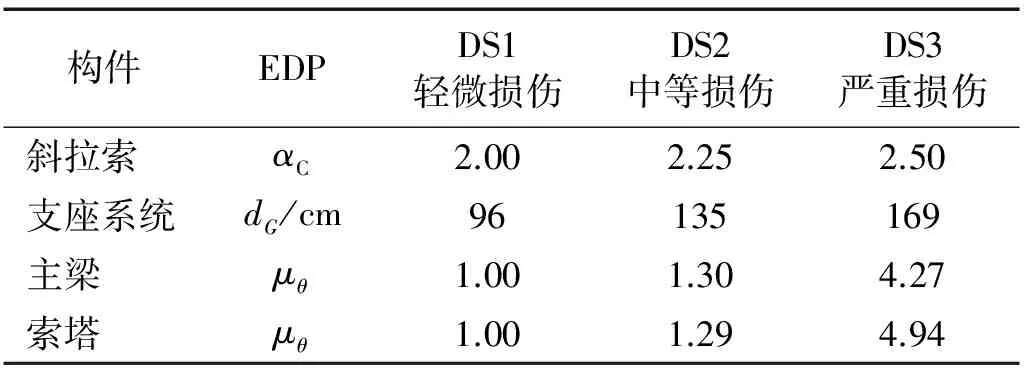
表2 构件损伤状态及损伤指标

4.3 地震动强度指标

选择合理的地震动强度指标是建立概率地震需求模型的一个重要环节。合理的地震动强度指标能够减小地震响应预测的离散性。在梁式桥易损性分析中，往往采用地震波峰值加速度PGA或谱加速度SA。研究表明，长周期结构选择位移型地震动强度更加合理[20-21]。因此，本文采用峰值谱位移PSD作为地震动强度指标。图6所示为基于PSD得到的概率需求模型。从图6可知，PSD和各类响应的拟合效果均十分理想。因此，采用PSD作为地震动强度指标能够满足要求。

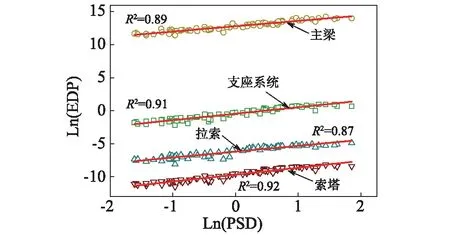
图6 基于PSD的概率需求模型Fig.6 Probability seismic demand model base on the PSD

5 非减震结构地震易损性评估

在研究减震控制效果前，首先对非减震结构的抗震性能进行评估。根据前述的易损性理论，结合结构概率需求模型及损伤模型，可以建立各构件易损性曲线。为了更好的反映结构整体的损伤特性，本文同时采用Monte-Carlo抽样方法[22]建立桥梁结构的系统易损性曲线。其中，桥梁系统的损伤状态基于串联假定，依据构件损伤模型确定。

图7所示为非减震桥梁在不同损伤状态下，构件及桥梁易损性曲线。从图7可知，三种损伤状态下，各构件之间的损伤关系基本一致。其中，支座系统是最易损伤的构件，这和常规桥梁的损伤特征相似。值得注意的是，主梁是仅次于支座系统的第二易损构件。但对于梁式桥，甚至常规低墩斜拉桥，主梁在纵向地震作用下并不会引起显著损伤，出现这种差异是因为索塔纵向刚度随着桥墩高度的增加而显著降低，墩顶在强震作用下将出现较大的转角，进而通过塔梁刚性连接传递给纤细的主梁，导致主梁产生显著损伤。由此可以看出，在进行此类桥梁的易损性评估时，有必要考虑主梁的损伤。此外，由于索塔和主梁的较大变形，加剧了拉索的轴向变形。因而，斜拉索也呈现出较高的损伤概率。除了以上三类较易受损的构件，索塔也表现出一定的损伤概率，但由于高墩具有良好的延性水平，索塔损伤程度远低于前三类构件，并且随着损伤程度的增加，这种差异更加显著。另一方面，对比边塔(5#索塔)和中塔(6#索塔)的损伤可以看出，中塔损伤概率明显高于边塔，这是由于中塔与主梁之间采用了固结连接形式，而边塔和主梁纵向并无连接。非一致的塔梁连接形式使得中塔的组合抗推刚度明显大于边塔。在地震作用下，抗推刚度大的索塔会吸收更多的地震能量，因而中塔比边塔更加容易损伤。

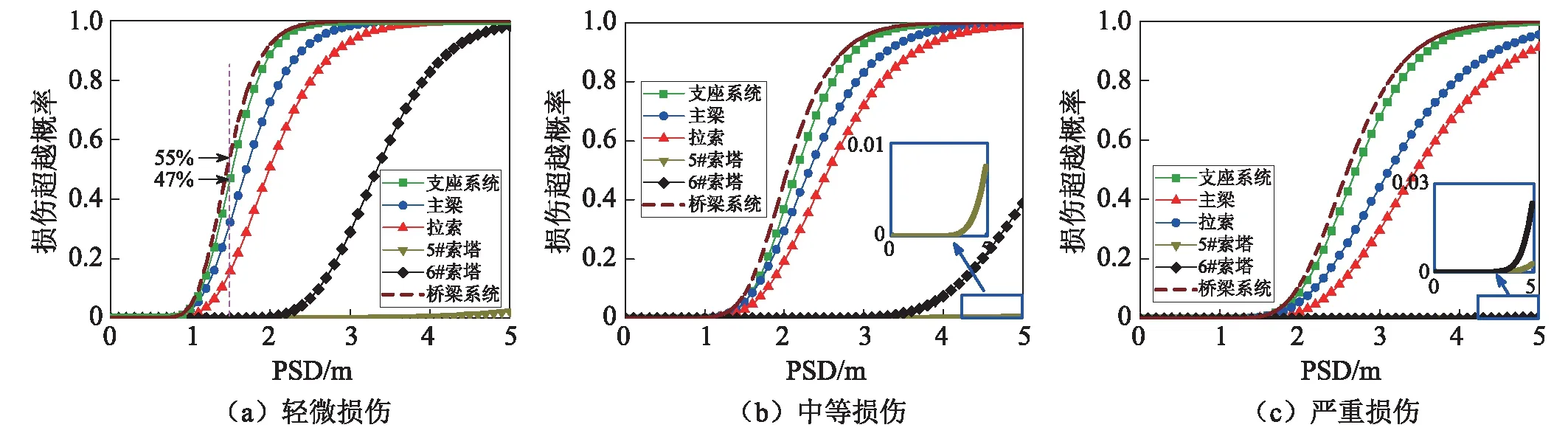
图7 构件及系统易损性曲线Fig.7 Components and bridge system fragility curves

对比桥梁系统和各构件易损性曲线可以看出，桥梁系统和支座系统的损伤概率非常接近，例如在PSD=1.5 m时，支座系统和桥梁系统的轻微损伤概率分别为47%和55%。这是由于桥梁系统的损伤取决于各构件的损伤，而支座是各类构件中最易受损的，支座的损伤很大程度上控制了整个桥梁系统的损伤，因而两者易损性曲线最为接近。同时可以看出，桥梁系统的损伤概率高于任何一个构件，这意味着地震作用下，桥梁系统较单个构件更易发生损伤。

6 减震效果研究

由前述分析可知，桥墩高度的增加降低了结构整体的刚度，导致支座系统、拉索、主梁呈现出较高的损伤，而控制结构的位移和变形对减轻结构损伤有关键作用。本节首先研究两类控制方式在不同控制参数及布置形式下减震效果的变化规律，最后结合实际情况确定本桥最优的减震控制方案。

6.1 黏滞阻尼器减震效果

图8所示为不同阻尼系数下，桥梁系统中等损伤易损性曲线的包络图。为衡量抗震性能的优劣，定义MPSD (Median PSD)为失效概率为50%时的PSD大小。MPSD越大，表明达到相同失效概率的地震动强度更高，结构抗震性能更好。由图8可知，当采用塔梁布置形式时，MPSD从原结构2.04 m增大到2.14～2.61 m，增幅为5%～57%；当采用梁端布置形式时，MPSD从2.04 m增大到2.34～3.75 m，增幅为18%～84%，两者的差异表明黏滞阻尼器的布置形式对减震效果有明显影响，阻尼器布置在梁端的效果明显优于布置在塔梁之间。

另一方面，对于塔梁布置形式，桥梁系统的MPSD最高出现在C=10 000 kN·s/m时，而并非在阻尼系数最大的时候，这表明阻尼系数对减震效果的影响并非单调变化，而是存在最优的阻尼系数使得阻尼器减震效果最理想；而对于梁端布置形式，桥梁系统的MPSD最高出现在C=22 000 kN·s/m，即阻尼系数最大的时候，这表明阻尼系数对结构减震效果的影响可能呈现出单调变化的趋势，较大的阻尼系数能获得更好的控制效果。

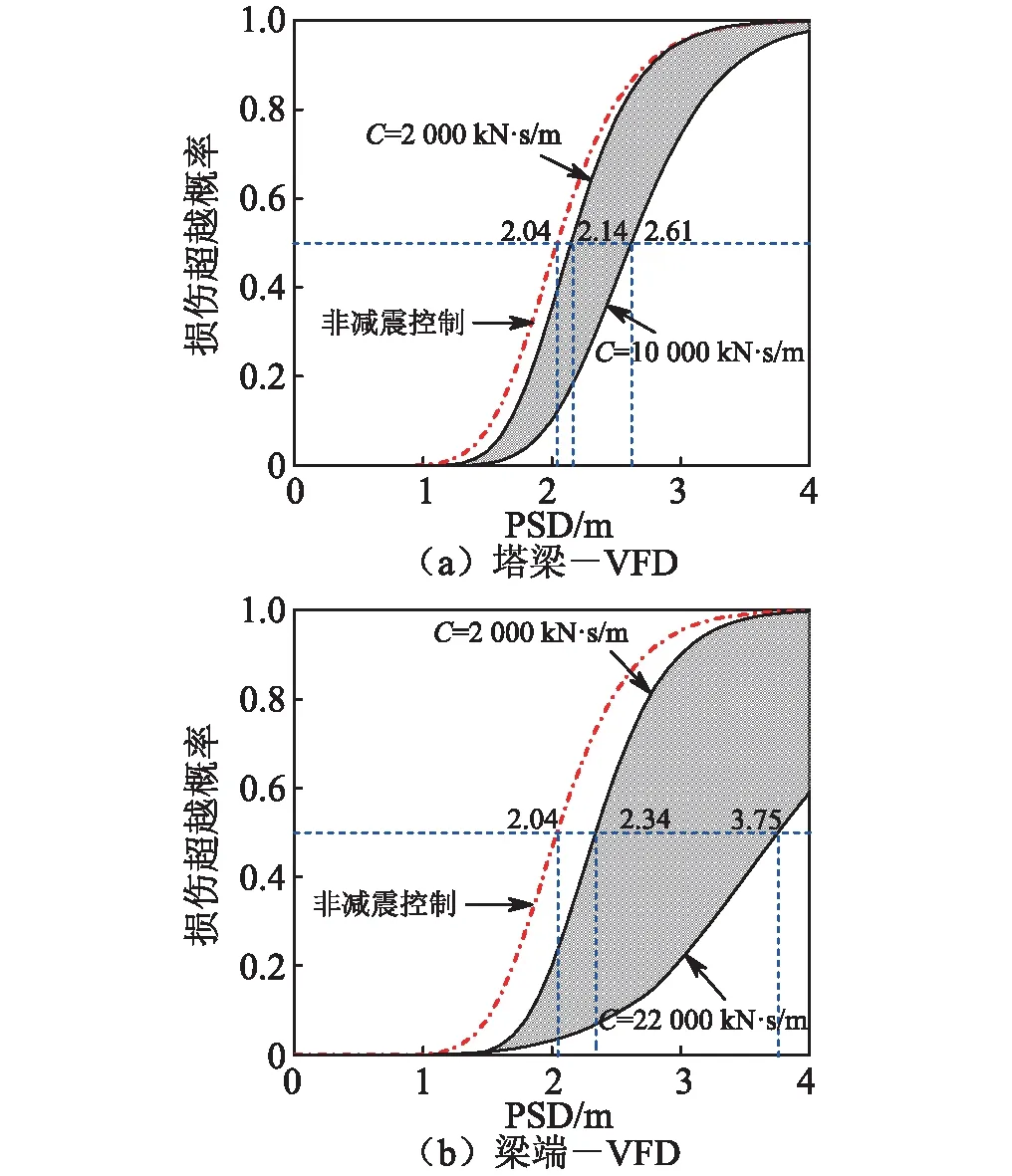
图8 不同阻尼系数下中等损伤系统易损性包络Fig.8 System fragility curve envelope at moderate damage under different damping coefficient

为了更加深入地研究阻尼系数对各构件损伤程度的影响，各构件中等损伤MPSD随阻尼系数的变化规律，如图9所示。总体而言，不同布置形式下，各构件的变化规律呈现显著差异；对于相同的布置形式，不同构件也存在不完全相同的变化，呈现这种差异的主要原因在于两种布置形式下主梁惯性力的传递方式发生了改变。当阻尼器采用塔梁布置形式时，主梁的部分惯性力通过阻尼器传递至边塔，在一定程度上增加索塔的地震需求。由于主梁和中塔采用固结形式，因此索塔的变形和支座系统、拉索、主梁的损伤相互耦合。当阻尼系数较小时，阻尼器产生的阻尼力较小，索塔的地震需求并未显著增加，而阻尼器耗散了结构部分能量，因而支座系统、主梁和拉索和索塔的MPSD呈现上升的趋势；当阻尼系数达到一定程度后，随着阻尼系数不断增加，阻尼器产生的阻尼力显著增大，加剧了索塔的变形，促使其他构件产生更大的损伤，因而 MPSD随后呈现降低的趋势。相反，当阻尼器布置在梁端，主梁的惯性力并不会传递至边塔。随着阻尼系数的增加，阻尼器的耗能能力不断增强，因而，各构件的MPSD呈现单调上升的特点。

值得注意的一点是，在塔梁布置形式下，四种构件均呈现出先增后减的趋势，这就意味对于不同构件可能存在多个最优阻尼系数，但观察桥梁系统的MPSD可知，最优阻尼系数出现在C=10 000 kN·s/m时，与支座系统的最优阻尼系数一致。这表明，桥梁系统的最优阻尼系数取决于最易受损的构件。

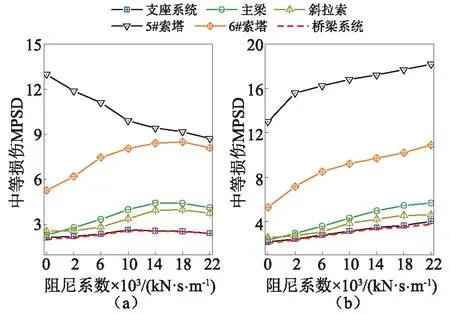
图9 不同阻尼系数下中等损伤MPSDFig.9 Median PSD of moderate damage under different damper coefficient

6.2 铅芯橡胶支座减震效果

不同屈服荷载下，桥梁系统中等损伤易损性曲线的包络图，如图10所示。首先对比两种布置形式的减震效果。对于塔梁布置形式， 最大MPSD为2.34 m，较非隔震桥梁增加15%，对于梁端布置形式， 最大MPSD为2.83 m，较非隔震桥梁增加39%。从图10可知，对于铅芯橡胶支座而言，在梁端布置的减震效果同样优于在塔梁之间布置，这与黏滞阻尼器的情况相似。另一方面，对于塔梁布置形式，减震效果最好的情况出现在屈服荷载F=15 000 kN时，并非在屈服荷载最大的时候，这表明屈服荷载对减震效果的影响同样呈现出非单调的规律。需要值得注意的是，当屈服荷载F=30 000 kN时，结构的MPSD为1.97 m，较非隔震结构2.04 m有所降低，说明此时的结构失效概率高于非减震结构，表明采用屈服荷载过大的铅芯橡胶支座，不仅不能减轻结构损伤，反而会加剧结构的破坏。而对于梁端控制形式，桥梁系统的失效概率最低出现在F=30 000 kN，这表明屈服荷载对结构减震效果的影响可能呈现出单调变化的趋势，随着屈服荷载的增加，铅芯橡胶支座的减震效果逐渐增强。

图10 不同屈服荷载下中等损伤系统易损性包络Fig.10 System fragility curve envelope at moderate damage under different yield force

不同屈服荷载下，各构件中等损伤MPSD的变化规律，如图11所示。当铅芯橡胶支座布置在塔梁之间，5#索塔MPSD呈现下降的趋势，6#索塔MPSD先增加后降低，最后两种构件MPSD趋于一致，这和布置黏滞阻尼器一致，说明塔梁设置减震控制装置能改善各塔损伤的不均匀性；然而，相比采用黏滞阻尼器的情况，采用铅芯橡胶支座的5#索塔MPSD降低程度明显高于6#索塔增加程度。这意味着铅芯橡胶支座在增加边塔损伤的同时，并未显著降低中塔损伤，这间接的说明了铅芯橡胶支座耗能能力相对较弱。对于主梁、拉索两类构件，随着屈服荷载的增加，MPSD呈现出单调增加的趋势，这和黏滞阻尼器的情况有所不同，这可能是由于支座刚度在屈服荷载增加的同时也在增加所导致的。

对于在梁端布置铅芯橡胶支座而言，各构件的MPSD均随着屈服荷载的增加单调上升，这和梁端黏滞阻尼器的变化规律一致。但相比而言，各构件MPSD的变化幅度均小于黏滞阻尼器，这同样也说明了铅芯橡胶支座耗能能力相对较弱。

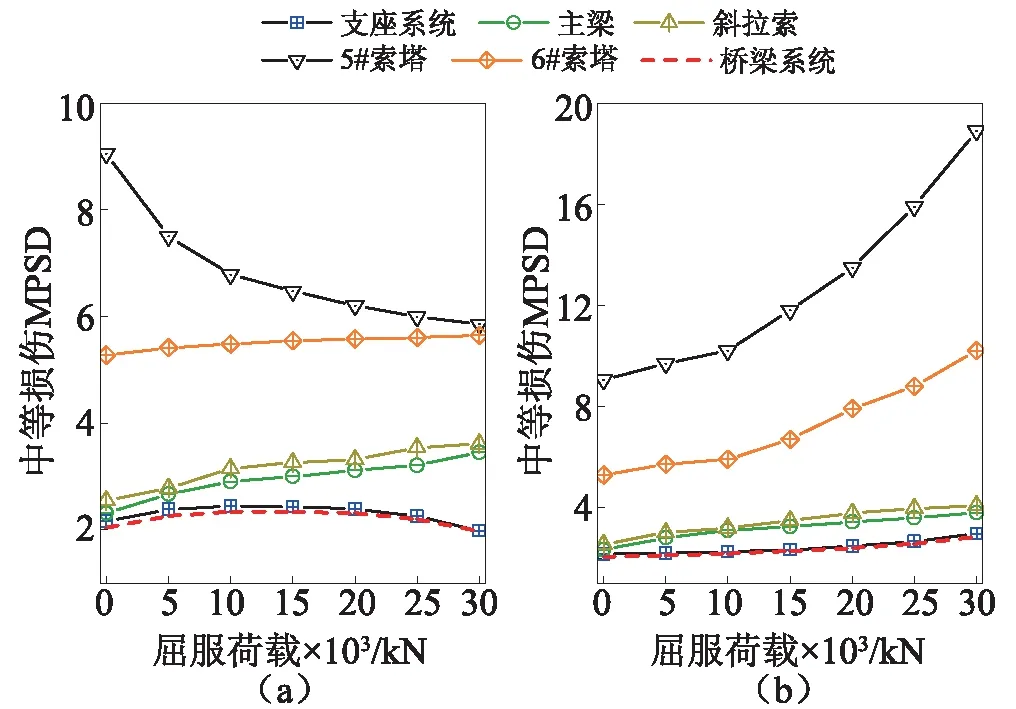
图11 不同屈服荷载下中等损伤MPSDFig.11 Median PSD of moderate damage under different yield load

6.3 最优减震方案比选

由以上分析可知，无论是铅芯橡胶支座还是黏滞阻尼器，当采用塔梁布置形式，存在最优的控制参数使得结构抗震性能最优；当采用梁端布置形式，则应尽量选择较强的控制参数。然而，在实际工程中，梁端控制装置往往需要固定在过渡墩或者桥台。控制装置过大会增加这些构件的损伤，为了避免墩台出现损伤，梁端控制装置的参数也存在一个上限值。对于本桥而言，为避免过渡墩进入塑性阶段，墩顶水平力需要控制在11 000 kN内。考虑这个因素，结合前述的规律，分别确定两种减震控制方式在不同布置形式下，共计四种控制方案的最优控制参数：方案1——在主梁端部设置两个5 500 kN的铅芯橡胶支座。方案2——在两个边塔各设置4个15 000 kN的铅芯橡胶支座。方案3——在主梁端部设置两个5 500 kN·s/m的黏滞阻尼器。方案4——在两个边塔各设置4个10 000 kN·s/m的黏滞阻尼器。四种控制方案在不同损伤状态下的构件和结构MPSD，如表3所示。

由表3可知，对于黏滞阻尼控制方式，在考虑过渡墩的损伤后，依然是梁端布置形式(方案3)获得最好的效果；而对于铅芯橡胶支座，由于过渡墩抗震能力的限制，梁端布置形式(方案1)的效果并不如塔梁布置形式(方案2)。另一方面，对于三种损伤状态，各方案的优劣基本一致。这表明在实际方案选择过程中，可以采用任意一种损伤状态进行方案比选。结合以上的分析评估，对于本例桥梁，采用方案3，即在梁端各采用两个阻尼系数为5 500 kN·m的黏滞阻尼器能获得最佳的减震控制效果。

表3 不同减震方案MPSD

7 结 论

本文以一座高墩多塔斜拉桥为研究背景，根据结构受力特点，定义各构件的损伤指标，采用非线性时程分析方法，结合易损性分析理论，建立了支座系统、主梁、斜拉索及索塔的易损性曲线，通过参数分析，对比研究了位移型和速度型两类减震控制装置的减震效果。根据分析得到以下结论：

(1)索塔墩高的增加，在一定程度上增加支座系统、主梁和拉索的损伤，导致此三类构件均出现较高风险；相反，由于高墩延性能力的提高，索塔损伤明显低于其他构件。

(2)由于主梁位移和索塔变形的耦合关系，无论是位移型控制还是速度型控制方式，采用塔梁布置形式都存在最优设计参数，并且最优设计参数往往取决于支座系统；相反，采用梁端布置形式则呈现出单调变化的趋势，随着控制参数的增大，减震效果逐渐增强。

(3)对于同一类型的控制方式，布置在梁端的效果优于布置在塔梁连接处，并且速度型控制装置更加显著；对于相同的布置形式，采用速度型控制方式减震效果更为明显。

[ 1 ] 李建中,袁万城. 斜拉桥减震、耗能体系非线性纵向地震反应分析[J]. 中国公路学报, 1998(1): 73-78.

LI Jianzhong, YUAN Wancheng. Nonlinear longitudinal seismic response analysis of cable-stayed bridge systems with energy dissipation [J]. China Journal of Highway and Transport， 1998(1): 73-78.

[ 2 ] 张锴,郭文华. 大跨度斜拉桥铅芯橡胶支座的参数优化[J]. 重庆交通大学学报(自然科学版),2011,30(2): 200-203.

ZHANG Kai, GUO Wenhua. Parameter optimum of leadrubber bearings (LRB) in the long-span cable-stayed bridges [J]. Journal of Chongqing Jiaotong University (Natural Science) ,2011,30(2): 200-203.

[ 3 ] 焦驰宇,李建中,彭天波. 塔梁连接方式对大跨斜拉桥地震反应的影响[J]. 振动与冲击,2009,28(10):179-184.

JIAO Chiyu, LI Jianzhong, PENG Tianbo. The influence of deck-tower connection on the seismic response of long-span cable-stayed bridges[J]. Journal of Vibration and Shock, 2009, 28(10): 179-184.

[ 4 ] 叶爱君,胡世德,范立础. 超大跨度斜拉桥的地震位移控制[J]. 土木工程学报,2004,37(12): 38-43.

YE Aijun, HU Shide, FAN Lichu. Seismic displacement control for super-long-span cable-stayed bridges[J]. China Civil Engineering Journal,2004,37(12): 38-43.

[ 5 ] 刘彦辉,谭平,金建敏,等. 地震作用下全浮漂大跨斜拉桥耗能减震控制研究[J]. 振动与冲击,2015,34(8): 1-6.

LIU Yanhui, TAN Ping, JIN Jianmin, et al. Energy dissipation control for long span cable-stayed bridges as a full-floating system under earthquake [J]. Journal of Vibration and Shock, 2015, 34(8): 1-6.

[ 6 ] 赵国栋. 斜拉桥地震反应分析与减震设计[D]. 北京：北京交通大学,2008.

[ 7 ] 徐凯燕. 大跨度斜拉桥非线性地震反应时程分析及减、隔震研究[D].广州：华南理工大学,2009.

[ 8 ] HU S C, LI L F, WU W P. Seismic analysis for a novel super high-pier and multi-span cable-stayed bridge in china [C]// International Association for Bridge and Structural Engineering. Nara:IABSE, 2015:1-8.

[ 9 ] CHOI E, DESROCHES R, NIELSON B. Seismic fragility of typical bridges in moderate seismic zones [J]. Engineering Structures, 2004, 26(2): 187-199.

[10] PAN Y, AGRAWAL A K, GHOSN M. Seismic fragility of continuous steel highway bridges in New York state [J]. Journal of Bridge Engineering, 2007, 12(6): 689-699.

[11] 李立峰,吴文朋,黄佳梅,等. 地震作用下中等跨径RC连续梁桥系统易损性研究[J]. 土木工程学报,2012,45(10): 152-160.

LI Lifeng, WU Wenpeng, HUANG Jiamei, et al. Study on system vulnerability of medium span reinforced concrete continuous girder bridge under earthquake excitation [J]. Civil Engineering Journal, 2012, 45(10): 152-160.

[12] Federal Emergency Management Agency-ASCE. NEHRP commentary on the NEHRP guidelines for the seismic rehabilitation of buildings：FEMA 274[R]. Washington, D.C.: Federal Emergency Management Agency-ASCE,1997.

[13] Manual for menshin design of highway bridges: ministry of construction, Japan[M]. Oakland：Earthquake Engineering Research Center, University of California, 1994.

[14] SHOME N, CORNELL C, BAZZURRO P, et al. Earthquakes, records, and nonlinear responses[J]. Earthquake Spectra, 1998, 14(3): 469-500.

[15] CORNELL C, JALAYER F, HAMBURGER R, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526-533.

[16] HAZUS-MH MR4 Earthquake model technical manual [M]. Washington, D.C.: Federal Emergency Management Agency, 2003.

[17] PARK Y J, ANG A H S. Mechanistic seismic damage model for reinforced concrete [J]. Journal of Structural Engineering, 1985,111(4): 722-739.

[18] 陆本燕,刘伯权,刘鸣,等. 钢筋混凝土桥墩性能指标量化研究[J]. 中国公路学报,2010,23(6): 49-57.

LU Benyan, LIU Boquan, LIU Ming, et al. Quantitative research on reinforced concrete performance index of reinforced concrete bridge column [J]. China Journal of Highway and Transport, 2010, 32(6): 49-57.

[19] 公路斜拉桥设计细则: JTG/TD 65-01—2007. [S]. 北京：人民交通出版社,2007.

[20] 李雪红,李晔暄,吴迪,等. 地震动强度指标与结构地震响应的相关性研究[J]. 振动与冲击,2014,33(23): 184-189.

LI Xuehong，LI Yexuan，WU Di，et al. Correlation between ground motion intensity and structural seismic response [J]. Journal of Vibration and Shock,2014,33(23): 184-189.

[21] 叶列平,马千里,缪志伟. 结构抗震分析用地震动强度指标的研究[J]. 地震工程与工程振动,2009,29(4): 9-22.

YE Lieping, MA Qianli, MIAO Zhiwei. Study on eart-hquake intensities for seismic analysis of structures [J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(4): 9-22.

[22] ALFREDO H S, TANG W H. Probability concepts in engineering [J]. Planning, 2007, 1(4): 1-3.

Seismiccontrolformulti-spancable-stayedbridgewithhigh-piersusingseismicfragilitymethod

HUSicong1,LILifeng1,2,WANGLianhua1,2

(1.CollegeofCivilEngineering,HunanUniversity,Changsha410082,China；2.KeyLaboratoryforWindandBridgeEngineeringofHunanProvince,HunanUniversity,Changsha410082,China)

In order to investigate the effect of seismic control devices on multi-span cable-stayed bridges with high piers, a cable-stayed bridge with 178-meter piers was taken as an example and the nonlinear finite element model was built. A series of 80 ground motions were selected from the Pacific Earthquake Engineering Research Center database and the nonlinear history analysis was conducted. The damage indexes of various components were defined according to the structure characteristics. Based on the fragility method, components and bridge system fragility curves were established, respectively. The seismic control effect of Displacement-type and Velocity-type control devices, represented by the lead rubber bearing (LRB) and the viscous fluid damper (VFD), with different parameters and arrangement forms was compared and investigated through fragility curves. At last, the optimal seismic control of the bridge was determined. The results show that the damage probability of bearings, the deck and cables increase significantly and one of towers becomes slighter with the height of piers. Due to different transmission mechanism of inertial force, the influence of seismic control parameter presents discrepancy for different arrangement forms. The device installed at the end of deck is superior to those installed between the deck and towers. For the same arrangement form, Velocity-type control device is more effective than the Displacement-type control device.

bridge engineering; multi-span cable-stayed bridge; high piers; seismic control; seismic fragility assessment; lead rubber bearing; fluid viscous damper

国家自然科学基金(51278183)

2016-05-04 修改稿收到日期： 2016-07-06

胡思聪 男，博士生，1990年生

李立峰 男，博士，教授，1971年生

U442.5+5

A

10.13465/j.cnki.jvs.2017.22.024