遗传计算题中的范围确定

2017-11-28陈永生安徽省桐城中学安徽安庆231403

中学生物学 2017年10期

关键词：表现型易错定律

陈永生（安徽省桐城中学安徽安庆 231403）

遗传计算题中的范围确定

陈永生（安徽省桐城中学安徽安庆 231403）

在遗传题的概率计算中因为对考查对象的范围确定不清，会导致计算方法或者结果错误，下面就在教学中发现的常见的学生易错点进行总结分析。

1 发生特定条件情况的计算对象范围确定

1.1 患病条件是否发生的计算范围确定

1.1.1 例题分析

【例1】若某常染色体单基因隐性遗传病，致病基因分别由A、a表示（图1），一对表现型均正常的夫妇生下了一个正常的女儿和一个患病的儿子，问该正常女儿是杂合子的概率为____________？

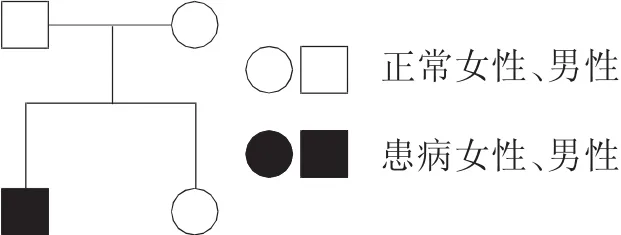
图1 某遗传病的系谱图

因为子代中儿子已被确定患病，则可反推该对表现型正常夫妇的基因型为Aa、Aa，由此可知后代表现型正常个体的基因型及比例分别为1/3AA、2/3Aa，故为杂合子概率为2/3。

1.1.2 易错归纳

实际计算中学生易忽略“表现型正常”个体这个范围，把计算范围等同于“正常与患病都可发生”的情况。这样就将计算范围扩大，自然无法得出正确答案。1.1.3 总结运用

这样的问题在很多场合都会出现，例如经常求子代某特定表现型中的纯合子与杂合子的比例，就不能用所有子代作为对象范围来考虑。在做题过程中一定要理清思路，把握题意，严格限定对象的条件范围。

1.2 性别条件是否确定的计算范围确定

1.2.1 例题分析

【例2】若一红绿色盲携带者女性与一正常男性婚配，则他们生下一患病儿子的概率是多少？若他们生下一儿子，其患病概率是多少？

根据夫妻表现型可推知其基因型依次为XBY、XBXb，则其后代若生一患病孩子，其基因型为XbY,为男性患者，概率为1/4；若已经生下一男孩，则其基因型有两种且概率皆为1/2,即XBY、XbY。

1.2.2 易错归纳

学生在计算这个问题时容易将“孩子还未出生时的预测”混同为“已经生下一男孩的预测”。这两个事件所包含的范围明显不同，前者还包含生下女孩的情况，而后者已经确定是男孩，则计算范围明显不同。

1.2.3 总结运用

由此可以得知，在计算这类问题时一定要区分“事件还未发生时的情况”与“已经发生某一事件的情况”的对象范围，即前者一般是总体范围而后者则是限定范围。在计算时一定要根据题意的表述，详细界定考查对象的范围。

2 事件之间是否有关联性的计算范围确定

2.1 无关联性事件的计算范围确定

2.1.1 例题分析

【例3】若一植物高茎（A）对矮茎（a）为显性，红花（B）对白花（b）为显性，这两对性状独立遗传，则基因型为AaBb的该植物个体自交一次后去除所有白花植株，问再自交一次后子代中高茎植株的比例？

因为这两对基因独立遗传，某一性状的去除对另一性状的比例无影响（实质是另一性状中的各基因型按比例同等减少），又或者可以运用进化论的观点，即人工选择对花色有影响，而对茎的高度无影响。则此时，只需计算Aa一对基因自交两次后代中显性个体的比例即可，高茎个体为3/8+1/4=5/8。2.1.2 易错归纳

对此题，学生最易犯的问题是不加思考，直接按照题目设计的过程进行计算。虽然学生也可得出正确的答案，但是因为步骤繁琐，容易出错。而且由于某些类型的题目可能会自交更多的代数，则实际上这种方法的意义就不大了。选择正确的性状计算范围，能够减少计算量，是提高正确率的的重要手段。

2.1.3 总结运用

对于这种类型的题目，在纵览全题后，应该思考最后要求涉及的对象与选择操作的对象之间是否具有关联性，若无关联性（例如独立遗传），则可将两对等位基因的问题简化为一对等位基因的问题，将考虑对象的范围大大缩小，解题计算更加快速、准确。

2.2 关联事件的计算规律范围确定

2.2.1 例题分析

【例4】某植物基因型为AaBb，两对基因的位置关系如图2所示，则该植物自交后代中AABB个体的比例是多少（不考虑交叉互换）？

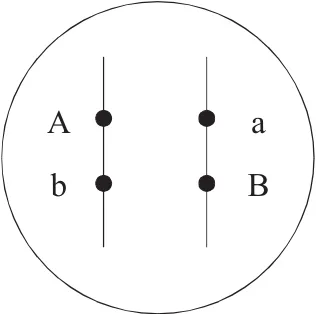
图2 两对基因的位置

根据图示可知，两对基因位于一对同源染色体，则不遵循自由组合定律，A与b连锁，a与B连锁，故只有两种等量配子Ab、aB产生，随机组合产生1/4AAbb、1/4aaBB、1/2AaBb,后代中的AABB个体的比例为0。

2.2.2 易错归纳

学生在做此题时易忽略两对基因位于同一对染色体上这一点，仍然当作是自由组合的题目，而实际上因为基因连锁而使配子只有两种，配子组合形式、自交结果当然与自由组合不同。

2.2.3 总结运用

在针对两对基因的计算问题中，一定要从题目中提取出是否遵循自由组合定律的条件，以确定计算规律的适用范围。一般题目会有较明确的提示，如“两对基因位于不同的染色体上”“两对基因不位于同一对染色体上”等。若无以上一般条件则要考虑是否有符合基因连锁的情况。

3 针对特定遗传计算规律的模型范围选择

3.1 哈温定律的条件范围确定

3.1.1 例题分析

【例5】某单基因隐形遗传病（以B、b表示相应基因）在人群中的患病率是1/100，则一对无血缘关系的表现型正常的夫妻生下一个患病孩子的概率是多少？

由题可知，应当将人群在一段时间内看作是一个遗传平衡的群体，即符合哈温定律的要求，则有Pbb=Pb2=1/100,即 Pb=1/10。又因（PB+Pb）=1,则 PB=9/10。而表现型正常的夫妻后代若有患病个体，则此夫妻两人基因型为 Bb、Bb，表现型正常的人为 P=（1-1/100=99/100），杂合个体为 PBb=2×PB×Pb=18/100,故在表现型正常的人中杂合子出现的可能为PBb/P=2/11。那么该对夫妻生下患病孩子的概率为2/11×2/11×1/4=1/121。

3.1.2 易错归纳

对于这种题型，学生易犯两个错误：① 不知道应该适用哈温定律，在这种情况下做此题则根本没有入手之处；② 在使用哈温定律后，将表现型正常的群体混同于整个人群（含患病个体），则最后的结果会偏大。3.1.3 总结运用

哈温定律的适用范围通常要满足以下几个条件：群体较大、自由交配、没有基因突变与自然选择、没有迁入迁出，即不产生进化的能够自由交配的种群。在题型考查中一般要注意是否已发生进化，或者是否满足以上几个条件，尤其经常以自由交配作为考查点，作为是否能使用哈温定律的限制条件。