面向缺失像素图像集的修正拉普拉斯特征映射算法
2017-11-28孙晓龙王靖杜吉祥
孙晓龙, 王靖, 杜吉祥
(华侨大学 计算机科学与技术学院, 福建 厦门 361021)

面向缺失像素图像集的修正拉普拉斯特征映射算法
孙晓龙, 王靖, 杜吉祥
(华侨大学 计算机科学与技术学院, 福建 厦门 361021)
针对缺失像素图像集,提出修正的拉普拉斯特征映射算法.该算法将缺失像素图像集看成向量集,利用向量之间的余弦相似度衡量缺失像素图像之间的距离,提出一种新的权值构造函数,并在多组标准测试数据集上进行实验.结果表明:修正的拉普拉斯特征映射算法可以很好地挖掘缺失像素图像数据集的内在流形结构,减弱缺失像素带来的不良影响.
流形学习; 缺失像素; 拉普拉斯特征映射; 余弦相似度
在信息化时代,如何对产生的大量高维数据进行有效的分析,并从中挖掘出所需要的本质信息显得尤为重要,而数据降维技术正是一种有效的处理方法.常见的传统数据降维方法有主分量分析(PCA)[1]、线性判别分析(LDA)和多维尺度变换(MDS)[2]等,这些方法可对线性结构的数据进行学习,但它存在的缺点是不能充分地处理复杂的非线性数据.流形学习方法相对于传统的线性维数约简方法能够较好地挖掘出隐藏在高维数据中的流形结构.代表性的流形学习方法有等距映射(ISOMAP)[3]、局部线性嵌入(LLE)[4]、拉普拉斯特征映射(LE)[5]和局部切空间对齐(LTSA)[6].Schafer等[7]先将缺损整数据中的缺失值按照某种原则和方法进行填充,再挖掘出填充后数据的本质信息.通常的填充方法主要有人工填补法、单值填补法(singular imputation,SI)[8]、EM(expectation maximization)算法[9-10]等;而针对缺损数据进行主成分分析,也有一些改进算法[11-14],但是这些都无法很好地挖掘缺损数据之间的非线性关系,而且还会带来累计误差[15].因此,迫切需要在缺损数据挖掘中引入非线性降维方法即流形学习.詹宇斌等[16]基于EM算法的主成分分析法[17],提出一种改进的LTSA算法(EM-LTSA).但是由于EM-PCAM作用于每个局部邻域,所以当缺失像素较多时,只用局部邻域的特征难以准确地提取主成成分,影响算法的有效性.目前,流形学习关于缺损数据的相关研究还比较少.一方面,对缺损数据难以准确构造局部邻域;另一方面,对数据的局部几何结构难以准确挖掘缺损.因此,本文提出一种修正的拉普拉斯特征映射算法.
1 修正的拉普拉斯特征映射
LE是经典的流形学算法,其基本思想是在高维空间中离得很近的点投影到低维空间中的点也应该离得很近.LE算法首先通过计算任意两个样本点之间的欧氏距离,寻找样本点最近的k个样本点构成局部邻域.然后,用图的方式构造局部邻域关系.通过选用指数衰减函数的方式构造样本点之间的权值,并在高维空间上构造反映样本点之间局部关系的权值矩阵W.最后,通过极小化带有约束条件的价值函数计算样本点的低维嵌入坐标.当图像出现缺失像素时,使用传统的欧氏距离无法准确地估计图像之间的距离,进而不能正确地构造局部邻域和权值矩阵,所以传统的LE算法无法从具有缺失像素的图像集中挖掘出其内在的流形结构.
对于每副ppx×qpx的图像将其变成一个m(m=p×q)维的图像向量xi(i=1,2,…,n),考虑图像集中包含具有缺失像素的图像,对于图像向量xi(i=1,2,…,n)定义一个缺失像素标记向量fi=(fi,1,fi,2,…,fi,m)T.该标记向量初始值为全1向量,fi,j=0表示当且仅当图像向量xi(i=1,2,…,n)中的第j个像素缺失,则整个图像集的缺失标记矩阵Fi(i=f1,f2,…,fn).
为了能够在缺失像素图像集上正确地构造局部邻域和权值矩阵W,对LE算法进行如下2点改进.
1) 基于缺失像素图像集,构造近邻图G(V,E).基于余弦相似度的基本思想,两个具有缺失像素的图像xi和xj之间的距离可以表示为

式(1)中:I表示图像xi和xj已知像素的指标集.两幅图像向量的余弦相似度sim(xi,xj)的范围为[0,1],相似度越大,距离越小.在具有缺失像素的图像集上使用文中提出的距离估计方法,得出任意两个图像之间的距离.以每个样本点为图的顶点,当点xi与xj互为近邻点时,G图有边,构造出合适的近邻图G(V,E).
欧氏距离是最常见的距离衡量方式,传统的拉普拉斯特征映射算法就是由样本点之间的欧氏距离来确定样本点的近邻点,从而构造近邻域.欧氏距离衡量的是空间中各点间的绝对距离,由各个样本点所在的位置坐标(即个体特征维度的数值)直接决定,即

式(2)中:欧氏距离体现了样本点数值特征的绝对差异,更多地从维度的数值大小体现差异,对绝对的数值敏感.余弦相似度则是最常见的相似度度量,余弦相似度衡量的是空间向量之间的夹角,体现的是样本点向量方向上的差异,而非距离或长度上,对绝对的数值不敏感.
假设图像数据集在没有缺失像素的情况下,样本点xi的一个近邻样本点为xj,一个非近邻样本点为xl.显然,dist(xi,xj)≤dist(xi,xl)或者sim(xi,xj)≥sim(xi,xl).当样本点xj,xl出现缺失像素时,因为欧氏距离由个体特征维度的数值直接决定,对绝对数值敏感,其大小极易受到像素值缺失的影响,则dist(xi,xj)≥dist(xi,xl),改变了原有正确的大小关系.而余弦相似度衡量的是样本向量方向上的差异,对绝对数值不敏感,其大小不易受到像素值缺失的影响,则sim(xi,xj)≥sim(xi,xl),仍然保持了其原有正确的大小关系.因此,余弦相似度衡量缺失像素图像之间的距离,可以正确地构造近邻图G(V,E),极大地减弱因缺失像素所带来的不良影响.文中提出的距离衡量方法不仅实现了正确地构造局部邻域,同时也为提出新的权值构造函数提供了基础.
2) 基于缺失像素图像集,提出新的权值构造函数.在已知像素上求解其图像向量的余弦相似度衡量两幅图像之间的距离,显然,当图像已知像素的个数越少时,这种方式得出的距离的可靠性应该越低,其权值应该越小.基于上述分析,新的权值构造函数为
式(3)中:|I|为已知像素指标集I中像素的个数;m是图像的维数.余弦相似度越大,图像之间的相关性越大,权值应该越大.同时,在已知像素构成的向量上求解余弦相似度,并将其作为两幅图像之间距离的可靠程度.通过加入系数(exp(1-m/|I|)来衡量,其中,参数σ为固定值.当|I|接近为0或者余弦相似度接近为0时,其权值接近为0;当|I|接近为m并且余弦相似度接近为1时,其权值接近为1.
基于上述方法,对LE算法构造局部邻域和权值矩阵的步骤进行了改进,使其能够在具有缺失像素的图像集上正确地构造局部邻域和权值矩阵W.同时,通过对LE算法的分析也可以看出:仅构造局部邻域和权值矩阵的算法步骤与原始数据有关,最终计算低维嵌入坐标的步骤是对前面抽取的信息进行进一步的加工处理,与原始数据无关.所以,低维嵌入坐标的计算方法同LE算法一致,都是通过极小化带有约束条件的价值函数来实现,即
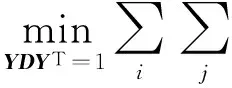

最终求解极小化问题归结为图拉普拉斯算子的广义特征值的问题.修正的拉普拉斯特征映射算法步骤为
输入:样本图像集矩阵X,邻域参数k,低维嵌入维数d,缺失标记矩阵F.
输出:样本图像集矩阵X对应的低维嵌入Y.
1) 利用式(1)计算图像集矩阵X中任意两幅图像之间的距离.当xj是xi的k个近邻中的一个点时,则认为它们是近邻的,即图G(V,E)有边(xi,xj).
2) 利用式(2)给构造的近邻图G(V,E)赋权值,获得权值矩阵W.
3) 计算低维嵌入结果.为了保持数据的局部特性,通过求解目标模型的极小化.求解问题转化为求解方程LY=λDY的广义特征值问题.低维嵌入坐标Y可由矩阵D1/2LD1/2的最小的第2个到第d+1个特征向量构成,即
Y=[u2,u3,…,ud+1]T.
2 数值实验
为了获得具有缺失像素的图像,每次实验中,随机从图像集选取部分图像,然后,构造缺失像素.构造缺失像素的方式有两种:一种是构造离散像素点的缺失,就是对每个选中的图像随机选取一定个数的像素点,将其像素值置为0,作为缺失像素;另一种是构造矩形区域像素的缺失,就是对每个选中的图像随机选取一个dx×dy大小的矩形块,将其像素置为0,作为缺失像素.同时,构建其对应的缺失标记矩阵F.在实验中,应用4种不同的对比算法对图像数据进行降维.
1) LE(original).将无缺失像素的图像集直接用LE[7]算法降维到低维特征空间.
2) LE(missing).将具有缺失像素的图像集直接用LE算法降维到低维特征空间.
3) LE(EM-PCAM)和LE(SI).先用EM-PCAM[13]或SI算法对具有缺失像素的图像数据集中的缺失像素值进行填充,然后,将填充后得到的图像集用LE算法降维到低维特征空间.
4) EM-LTSA.将具有缺失像素的图像集直接用EM-LTSA[13]算法降维到低维特征空间.
对低维嵌入后的结果采用K-NN(K-nearest neighbor)分类器进行分类,得到不同对比算法的分类效果.
2.1实验数据集
1) ORL(olivetti research laboratory)人脸图像集.该数据集共有40个人不同角度的人脸图像,每人10副图像,共包含了200个112 px×92 px的灰度样本点.
2) TEXTURE图像集.从USC-SIPI图像数据库中选取4张1 024 px×1 024 px的纹理图像,然后,将其分别裁剪成32 px×32 px像素子图,每张原图像裁剪得到4 356张子图.从每张原图得到的子图集中随机选取1 000张子图,构成一个包含4 000个32 px×32 px的样本点.
3) COIL-20-PROC图像集.该数据集包含20种不同的物品,每个物品在不同角度下的72张图像,构成一个包含1 440个128 px×128 px的样本点.
2.2实验结果与分析
对于所有流形学习算法都涉及到邻域参数k和目标维度d,参数k的选取范围设置在[4,17],其目标维度d的取值范围设置在[3,85],参数σ取值范围在[0.4,1.0].通过个重复3实验,选取最优参数,并列出其中最好的实验结果.
实验1.为验证面对不同缺失像素图像集时文中算法效果的通用性,将文中算法和上述的各对比算法在3种图像集上进行实验.ORL人脸图像、TEXTURE和COIL-20-PROC3种图像集构造矩形区域像素缺失的缺失区域大小(dx×dy)分别为60 px×60 px,16 px×16 px和60 px×60 px;3种图像集构造离散像素点缺失的缺失程度为50%(每副图片中缺失像素点的个数占总像素点个数的百分比).随机选取每个图像集中50%样本点作为训练集,剩下的样本点形成测试集.实验结果如表1所示.

表1 各算法在3种图像数据集上的分类正确率Tab.1 Classification correct rates on three different images data sets
由表1可知:当图像集有缺失像素存在时,LE算法在K-NN分类器下的分类的正确率都远远低于其他算法.这说明LE算法不能很好地学习缺损数据的内在流形结构.究其原因,LE算法在选择近邻域的步骤中,采用传统的欧氏距离衡量缺失像素图像之间的距离.欧氏距离的值极易受到像素值缺失的影响,从而无法准确地选择近邻域,最终影响算法效果.
由表1还可知:基于EM-PCAM填充算法虽然能够缓解缺失像素带来的不良影响,但这种效果是有限的.这是由于EM-PCAM算法作用于每个局部邻域,所以当缺失像素较多时,只用局部邻域的特征难以准确地提取主成成分,影响算法的有效性.基于同样的原因,EM-LTSA的改进效果也比较有限.基于SI[21]填充算法虽然比EM-PCAM算法有效,但是在TEXTURE数据集上改进效果也并不明显.这是因为单值填充算法忽略了缺失特征的不确定性,同时,还会带来累计误差.在这3个缺损数据集上,文中算法的分类准确率明显高于其他算法.在COIL-20-PROC数据集上,文中算法同LE算法在无缺损数据集上的识别率接近.这说明了文中算法面对具有缺失像素的图像集时,由于采用新的距离衡量方式和权值构造函数,极大地减弱了缺失像素值带来的影响,从而构造合适的近邻图和权值矩阵,所以可以很好地挖掘出图像集内在的流形结构.
实验2.为了进一步测试文中算法在不同缺失程度图像集上的鲁棒性,将上述各对比算法和文中算法在不同缺失程度的ORL人脸图像数据集上进行对比实验.ORL构造离散像素点缺失的缺失程度分别为20%,30%,40%,50%,60%,70%,80%,90%和95%.ORL构造矩形区域像素缺失的大小(dx×dy)分别为20 px×30 px,30 px×40 px,40 px×40 px,40 px×50 px,50 px×50 px,50 px×60 px,60 px×60 px,60 px×70 px和80 px×70 px.随机选取每个图像集中50%的样本点作为训练集,剩下的样本点形成测试集.实验结果,如图1所示.图1中:R为正确率;P为离散像素点缺失程度;S为矩形区域像素缺失的区域大小.

(a) 离散像素点缺失程度 (b) 矩形区域像素缺失的区域大小图1 不同算法在不同缺失程度ORL图像集上其分类正确率的变化Fig.1 Classification correct rates of ORL images set with different degree of missing for different algorithms
由图1可知:即使面对较少程度的像素缺失,如20%的离散像素点缺失和30 px×20 px的矩形区域像素缺失,LE算法的分类正确率也远低于其在未缺失像素图像集时的分类准确率(由实验1可知为90%).这表明LE对数据缺失程度具有很强的敏感性,主要是因为LE算法采用的欧氏距离衡量方法对缺失的像素值具有很强的敏感性.在离散像素缺失的情形下,LE (EM-PCAM)和EM-LTSA的准确率虽然高于LE算法的结果,但也对数据缺失程度具有很大的敏感性.这是因为EM-PCAM算法只作用于每个局部邻域,所以当缺失像素较多时,只用局部邻域的特征难以准确地提取主成成分,影响算法的有效性.面对较小程度的缺失,单值填充SI具有很好的效果,但也无法解决数据大规模缺失的问题.
因为单一的填充值忽略了缺失特征的不确定性,同时,随着缺失程度的增加还会带来累计误差,将会严重影响填充大规模缺失数据的效果.在此数据集上,文中算法体现了对数据缺损程度具有非常好的鲁棒性.即使离散像素缺失的程度达到95%,文中算法仍能保持很高的准确率,因为文中算法在选择近邻域的步骤中采用余弦相似度的度量方法.由上文的理论分析可知:余弦相似度的度量方法对像素缺失值不敏感,所以无论图像缺失程度变化如何,文中算法的分类正确率都可以保持在较高且稳定的区间值内,具有非常好的鲁棒性.
实验3.为了检测文中算法在不同训练点个数下的分类效果,在COIL-20-PROC图像集上做了进一步的测试实验.将规模为1 420的图像集按照不同的训练测试比(training∶testing)分为5组进行实验,其中,缺失像素的处理方式是构造离散像素点的缺失,缺失程度为50%.不同算法在每种训练测试比下的分类正确率,如表2所示.

表2 不同算法在COIL-20-PROC图像集上不同训练测试比下的分类正确率Tab.2 Classification correct rates of COIL-20-PROC images set for different training test
由表2可知:面对完整图像集,训练测试比越大,LE算法分类的准确率越高.当面对缺失像素图像集时,LE(missing),LE(EM-PCAM),LE(SI)和EM-LTSA的分类准确率则不具有这个规律,即更少的训练点,可能得到更好的分类效果.这主要是因为面对训练集中的缺损数据,这些方法无法准确挖掘出它们和测试数据之间的本质关系,即更多的缺损训练数据反而降低这些方法的分类效果.面对具有缺失像素的图像集,文中算法在所有的训练测试比上都体现出了最好的分类效果.值得注意的是,随着训练数据的增加,文中算法的分类效果也随着增加.这表明文中算法能很好地挖掘训练集和测试集中缺损数据的本质关系.
3 结束语
针对流形学习算法面对缺失像素图像集的这一特例,受余弦相似度度量方法的启发,提出了适用于缺失像素图像集的距离衡量方式和基于这种距离衡量方式的权值构造函数.对经典的拉普拉斯特征映射算法进行改进,提出一种修正的拉普拉斯特征映射算法.实验表明了文中算法的有效性.
[1] JOLLIFFE I T.Principal component analysis[J].Springer Berlin,2010,87(100):41-64.DOI:10.2307/3172953.
[2] COX T,COX M.Multidimensional scaling[J].Journal of the Royal Statistical Society Series A,1994,5(2):875-878.DOI:10.2307/2983485.
[3] TENENBAUM J B DE S V,LANGGORD J C.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(5500):2319-2323.DOI:10.1126/science.290.5500.2319.
[4] ROWEIS S T,SAUL L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290:2323-2326.DOI:10.1126/science.290.5500.2323.
[5] BELKIN M,NIYOGI P.Laplacian eigenmaps for dimension reduction and data representation[J].Neural Computation,2003,15(6):1373-1396.DOI:10.1162/089976603321780317.
[6] ZHANG Zhengyue,ZHA Hongyuan.Principal manifolds and nonlinear dimensionality reduction via tangent space alignment[J].Journal of Shanghai University,2005,26(1):313-338.DOI:10.1137/S1064827502419154.
[7] SCHAFER J L,GRAHAM J W.Missing data: Our view of the state of the art[J].Psychological Methods,2002,7(2):147-177.DOI:10.1037/1082-989X.7.2.147.
[8] 金连.不完全数据中缺失值填充关键技术研究[D].哈尔滨:哈尔滨工业大学,2013:1-55.
[9] LITTLE R J A,RUBIN D B.Statistical analysis with missing data[M].New York:John Wiley and Sons,2002:364-365.DOI:10.2307/3172915.
[10] DEMPSTER A P,RUBIN D B.Maximum likehood estimation from incomplete data via the EM algorithm[J].Journal of the Royal Statistical Society,1977,39(1):1-38.
[11] STANIMIROVA I,DASZYKOWSKI M,WALCZAK B.Dealing with missing values and outliers in principal component analysis[J].Talanta,2007,72(1):172-178.DOI:10.1016/j.talanta.2006.10.011.
[12] SERNEELS S,VERDONCK T.Principal component analysis for data containing outliers and missing elements[J].Comput Stat Data Anal,2008,52(3):1712-1727.DOI:10.1016/j.csda.2009.04.008.
[13] LI Yongming.On incremental and robust subspace learning[J].Pattern Recongnition,2004,37(7):1509-1518.DOI:10.1016/j.patcog.2003.11.010.
[14] DANIJEL S,LEONARDIS A.Incremental and robust learning of subspace representations[J].Image and Vision Computing,2008,26(1):27-38.DOI:10.1016/j.patcog.2006.09.019.
[15] WILLIAMS D,LIAO Xuejun,XUE Ya,etal.On classification with incomplete data[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(3):427-436.DOI:10.1109/TPAMI.2007.52.
[16] 詹宇斌,殷建平,李宽.缺失像素图像集的流形学习算法[J].吉林大学学报(工学版),2011,41(3):728-733.DOI:10.13229/j.cnki.jdxbgxb2011.03.014.
[17] ROWEIS S T.EM algorithm for PCA and SPCA[J].Advances in Neural Information Processing Systems,1999,10:626-632.DOI:10.1021/ja100409b.
(责任编辑: 陈志贤英文审校: 吴逢铁)
ModifiedLaplacianEigenmapAlgorithmforMissingPixelsImageSet
SUN Xiaolong, WANG Jing, DU Jixiang
(College of Computer Science and Technology, Huaqiao University, Xiamen 361021, China)
In this paper, we propose a modified laplacian eigenmaps algorithm for the missing pixel images. The algorithm takes the missing pixel image set as a vector set, then using the cosine similarity between vectors to measure the distance between missing pixel images. Further, a new weight constructor function is proposed. Experiments on several sets of standard test data sets show that the modified laplacian eigenmaps algorithm can well excavate the intrinsic manifold structure of the missing pixel images and weaken the negative effects of missing pixels.
manifold learning; missing pixels; laplacian eigenmaps; cosine similarity
10.11830/ISSN.1000-5013.201512067
TP 181
A
1000-5013(2017)06-0862-06
2015-12-28
王靖(1981-),男,教授,博士,主要从事模式识别、推荐系统的研究.E-mail:wroaring@hqu.edu.cn.
国家自然科学基金资助项目(61370006); 福建省自然科学基金资助项目(2014J01237); 福建省教育厅科技项目(JA12006); 福建省高等学校新世纪优秀人才支持计划(2012FJ-NCET-ZR01); 华侨大学中青年教师科技创新资助计划(ZQN-PY116)
