非对称区间上调和函数的Schwarz引理

李孟华, 陈行堤

(华侨大学 数学科学学院, 福建 泉州 362021)

非对称区间上调和函数的Schwarz引理

李孟华, 陈行堤

(华侨大学 数学科学学院, 福建 泉州 362021)

研究单位球到给定一般区间上的实调和函数的Schwarz型引理.运用调和函数的平均值定理，将像域在对称区间[-1,1]上的调和函数的Schwarz引理推广到在一般区间[a,b]上.作为一个应用，改进了Partyka和Sakan的一个结果，得到实调和函数的下界估计.

调和函数; Schwarz引理; Poisson核; 平均值定理

1 预备知识

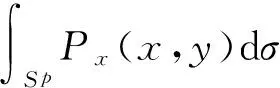
由于在单位球Bp上的调和函数满足平均值定理和Fatou定理[1]，因此,对于0lt;clt;1，可记

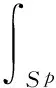
为了方便,记

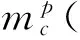
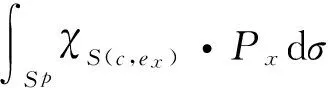
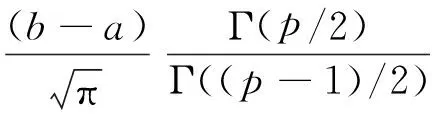
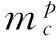
式(6)，(7)中：v=1；μ=p/2.

Heinz运用Schwarz引理得出单位圆盘到自身上的调和函数的Heinz不等式[2].基于此理论，Partyka等[3]用拟从属技巧，将Schwarz引理从条件|ReF(z)|lt;1推广为带形区域a≤ReF(z)≤b的情形[4]，有

并对其加以应用[5-6].许多学者对Schwarz引理进行深入研究[7-9].Kalaj等[9]研究单位球上实调和函数的模，并给出了相应的Schwarz引理.Burgeth[10]给出了单位球Bp上实调和函数满足条件-1≤h(x)≤1下的偏差估计.

2 主要结果及证明

命题1设h为单位球Bp上的实调和函数，且a,b∈R,alt;b.若a≤h(x)≤b，h(0)=d,则对于c=(d-a)/(b-a)和任意的x∈Bp，有

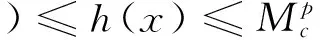
证明 首先，对于任意的t∈R+，x∈Bp测度函数σ(Pxgt;t)在R+上连续且是关于t的严格单调递减函数.因此，对任意的c∈[0,1]，都存在唯一的tc∈R+，使得σ(Pxgt;tc)=c·σ(Sp).从而有

).

由式(5)知：χ{Pxgt;tc}∈Kc.令x∈Bp,y∈Sp,|x|=r，则单位球Bp上的Poisson核为

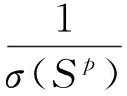
由于x·y=rcos(x,y)，因此，对固定的x,Px(y)的单调性由cos(x,y)确定，其中，(x,y)表示y到x的转角，从而当Px(y)gt;tc时,y的取值范围是以ex为中心的球S(c,ex)，即

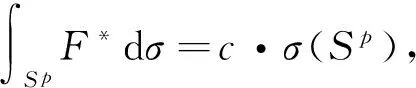
由上式及χSp-χS(1-c,ex)=χS(c,ex)，可得

定理1假设h为单位圆盘D上满足h(0)=0的调和映照，令a,b∈R且alt;b.若a≤h(x)≤b，则

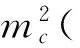
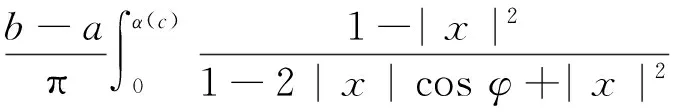
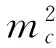
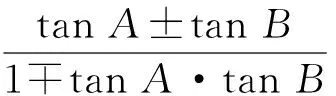
同理计算可得

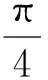
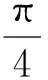
而文献[2]中所得结论为

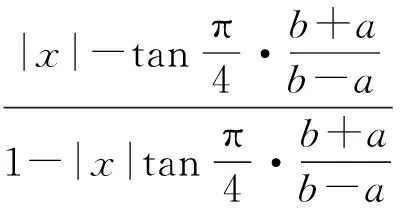
[1] AXLER S,BOURDON P,RAMEY W.Harmonic function theory[M].New York:Springer Verlag，2000.

[2] HEINZ E.On one-to-one harmonic mappings[J].Pac J Math,1959,9(1):101-105.

[3] PARTYKA D,SAKAN K.On a variant of Heinz′s inequality for harmonic mappings of the unit disk onto bounded convex domains[J].Bull Soc Sci Lett,2009,52(2):25-36.

[4] DUREN P.Harmonic mappings in the plane[M].Cambridge:Cambridge University Press,2004：75-77.

[5] PARTYKA D,SAKAN K.Three variants of Schwarz lemma for harmonic mappings[J].Bull Soc Lett,2006,51(2):27-34.

[6] PARTYKA D,SAKAN K.Quasiconformal and Lipschitz harmonic mappings of the unit disk onto bounded convex domains[J].Anna Acad Scie Fenn Math,2014,39(2):811-830.

[7] KALAJ D.Schwarz lemma for harmonic mappings in the unit ball[J].Proc Amer Math Soc,2010,140(1):161-166.

[8] PAVLOVIC M.A Schwarz lemma for the modulus of a vector-valued analytic function[J].Proc Amer Math Soc,2011,139(3):969-973.

[9] KALAJ D,VUORINEN M.On harmonic functions and the Schwarz lemma[J].Proc Amer Math Soc,2010,140(1):161-166.

[10] BURGETH B.A Schwarz Lemma for harmonic and hyperbolic-harmonic functions in higher dimensions[J].Manu Math,1992,77(1):283-291.

[11] DUREN P.Theory of-space[M].New York:Dover Publications,2000.

(责任编辑： 陈志贤英文审校： 黄心中)

SchwarzLemmaforHarmonicFunctionsinAsymmetricInterval

LI Menghua, CHEN Xingdi

(School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China)

In this paper, we investigate the Schwarz lemma for real harmonic functions of the unit ball into a general interval. By appealing to the method of mean-value theorem of harmonic functions, we obtain the Schwarz lemma of harmonic functions with their image domains generalized from the symmetric interval [-1,1] to a general interval [a,b]. As an application of this result, we improve the upper bound estimate given by Partyka and Sakan. Moreover, a lower bound for this class of harmonic functions is also given.

harmonic mapping; Schwarz lemma; Poisson kernel; mean-value theorem

10.11830/ISSN.1000-5013.201612009

O 174.55

A

1000-5013(2017)06-0898-05

2016-12-04

陈行堤(1976-)，男，教授，博士，主要从事函数论的研究.E-mail:chxtt@hqu.edu.cn.

国家自然科学基金资助项目(11471128); 福建省自然科学基金计划资助项目(2014J01013); 华侨大学青年教师科研提升计划资助项目(ZQN-YX110)； 华侨大学研究生科研创新能力培育计划资助项目(1511313002)