采用模糊层次分析法的PFMEA方法改进及应用

夏蓓鑫， 陈鑫， 李龙， 陶宁蓉， 张佳栋

( 1. 上海大学 机电工程与自动化学院， 上海 200072;2. 上海海洋大学 工程学院， 上海 201306)

采用模糊层次分析法的PFMEA方法改进及应用

夏蓓鑫1， 陈鑫1， 李龙1， 陶宁蓉2， 张佳栋1

( 1. 上海大学 机电工程与自动化学院， 上海 200072;2. 上海海洋大学 工程学院， 上海 201306)

为解决因各专家判断矩阵过于均一化而导致的风险排序与实际发生偏差的问题，在传统的基于模糊层次分析法的过程失效模式与分析(PFMEA)方法基础上做进一步的改进.从专家的个体区别和职业类别两方面考虑，分析专家判断矩阵变化程度对专家分组及评估各组别对专家权重的影响，进而合理设定专家权重.通过该改进方法在汽车空调冷凝器制造过程中的实际应用，验证方法的有效性.研究结果表明：改进的基于模糊层次分析法的PFMEA方法能更准确地对产品失效风险进行排序.

汽车空调冷凝器； 产品失效； 过程失效模式与分析法； 模糊层次分析法； 专家权重

作为可靠性工程领域的基本工具，过程失效模式与分析(process failure mode and effect analysis,PFMEA)主要应用于产品的生产制造过程[1-2].传统的PFMEA方法一般使用风险顺序数(RPN)来确定风险顺序[3]，但存在RPN分辨度不高和主观性与模糊性等两大主要缺陷[4-6].针对传统PFMEA方法存在的缺陷，国内外学者们通过引入模糊理论取得了大量的研究成果.门峰等[1]将模糊理论与灰色关联理论相结合改进了FMEA方法.盛精等[6]使用模糊理论与层次分析法构建了零部件制造工艺的风险评估模型，进而确定相关风险等级，从而提升了RPN的风险值分辨率.Bowles等[7]使用模糊逻辑规则来确定失效的优先级.杜晗恒等[8]提出模糊层次分析法(F-AHP)和模糊TOPSIS(technique for order preference by similarity to ideal solution)集成的方法，通过模糊层次分析评价法分配参数的权重，再应用TOPSIS方法获得各失效因素的分值并进行排序.王浩伦等[9]将三角模糊软集引入到FMEA方法中，利用三角模糊软集方法中AND运算对各评价专家的评价信息进行融合，进一步改进方法的效率.安相华等[10]将混合多属性决策和关联传播分析有机集合，解决了产品FMEA在不确定环境下的应用问题.耿秀丽等[11]考虑了故障模式之间的相互影响关系，通过决策与实验评价实验室方法对风险模式的净影响度进行了研究分析，从而对初始评估的严重度做了修正.然而，现有的基于模糊层析分析法的PFMEA方法在某些实际应用中仍存在一定的问题，如在引入专家组时将所有专家的判断平整化，没有考虑不同专家之间的区别.面对这类问题，现有的方法并不完善，其结果并不能完全反映样本的信息，统计结果往往会偏离实际.因此，本文在现有研究工作基础上，通过设定专家权重进一步改进PFMEA方法，并将所提方法应用在汽车冷凝器制造过程中.

1 基于模糊层次分析法的PFMEA方法

1.1判断矩阵构造

邀请K′位专家，成立专家小组， 对风险顺序数RNP的3个评价指标发生频度(O)、严重度(S)、探测度(D)进行比较分析并建立判断矩阵. 矩阵中的行、列分别按照 O，S，D顺序排列.对于第k个专家的

表1 评价指标数值的比较Tab.1 Comparison of evaluation index values

判断矩阵，有

判断矩阵中的数值为对应O，S，D之间的比较数值，其取值可以通过表1确定.表1中：整数表示前者和后者比的重要程度；倒数表示后者和前者比的重要程度；比较数值选取 2，4，6，8则表示介于相应比较程度之间.

1.2一致性检验

对判断矩阵Zk进行一致性检验，以确定专家的判断矩阵是否可以接受.相对一致性比例CR=CI/RI.其中，RI是平均随机的一致性指标，当矩阵阶数为3时，取RI=0.52；CI为一致性指标，CI=λmax-n/(n-1)，λmax为判断矩阵Zi的最大特征值，n为矩阵阶数，此处取3.通常情况下，CR越小，判断矩阵的一致性越好，文中将0.1作为判断矩阵一致性的阈值.当CR小于这个阈值时，说明判断矩阵的一致性是满意的；否则，将该专家剔除.经过一致性检验后，最终保留的专家数量设为K.

1.3评价指标的权重计算

1.3.1 判断矩阵的评价指标权重 对于第k个专家，可以根据其给出的判断矩阵Zk计算相应的3个评价指标的权重.设wki为由判断矩阵Zk计算得到的第i个指标的权重，将判断矩阵中的各元素按列进行归一化处理，再按行求均值.即有

1.3.2 专家权重的计算 区别于以往将专家无差别对待的研究方法，在计算得到每位专家的3个评价指标权重后，根据专家的个体区别和职业类别进行专家权重设定.设定专家权重主要基于以下两方面的考虑.一方面，为了能够反映个体的区别和意愿，采用通过个体样本的特征值λmax变化来反映其在整个样本中的影响程度.当n取3时，λmax取值范围为[3，3.104).为了和另一个指标相符，将该指标转变为极大型指标，得到调整公式为

式(3)中:Fk是第k个专家的判断矩阵的变化程度.

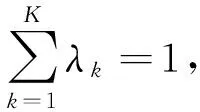
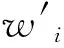
1.4模糊评价矩阵建立

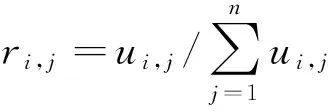
1.5模糊综合评价

结合客观评价和主观评价因素，即综合考虑评价指标权重集对指标的模糊评价矩阵影响，为专家组的模糊评价矩阵赋予不同的权重.设模糊综合评价矩阵为

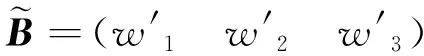
2 应用实例分析

以某汽车空调制造商按照客户和TS16949型制造冷凝器产品为例.制造工序包含为6道工序，依次为喷涂主片和封盖→插入隔片→压接集管→芯子装配→钎焊→最终装配，则分别将工序按先手顺序标记为A1，A2，A3，A4，A5，A6.潜在失效模式包括钎焊不良、隔片倾斜、主片封盖偏移、主片插坏、散热带掉落、螺栓松脱.潜在失效后果包括冷凝器泄露、内漏、影响性能、装配困难、冷凝器泄露、散热性能降低和震动试验不能通过.

使用未改进前的基于F-AHP的PFMEA方法可以得到各工序风险顺序,如表2所示.

表2 基于F-AHP的PFMEA方法的冷凝器各工序风险顺序Tab.2 PFMEA for automobile air conditioning condenser manufacture

将改进后的PFMEA方法应用到冷凝器制造中.首先，分别从质量、工艺、设计、生产、技术管理层各选出3名专家成立专家组，并建立评价指标判断矩阵，如表3所示.

表3 专家评价指标的判断矩阵Tab.3 Judgment index of expert evaluation index

对专家评价指标进行一致性检验结果，如表4所示.

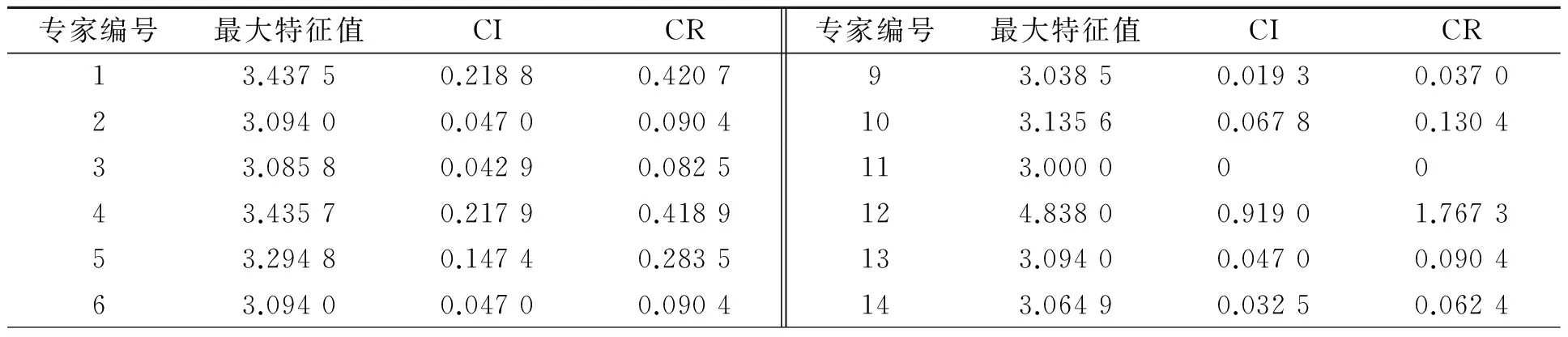
表4 专家评价指标的一致性检验Tab.4 Consistency test of expert evaluation index

续表Continue table

选择相对一致性比例CR小于0.1的10位专家进入最终的专家组，并根据判断矩阵确定指标权重，如表5所示.

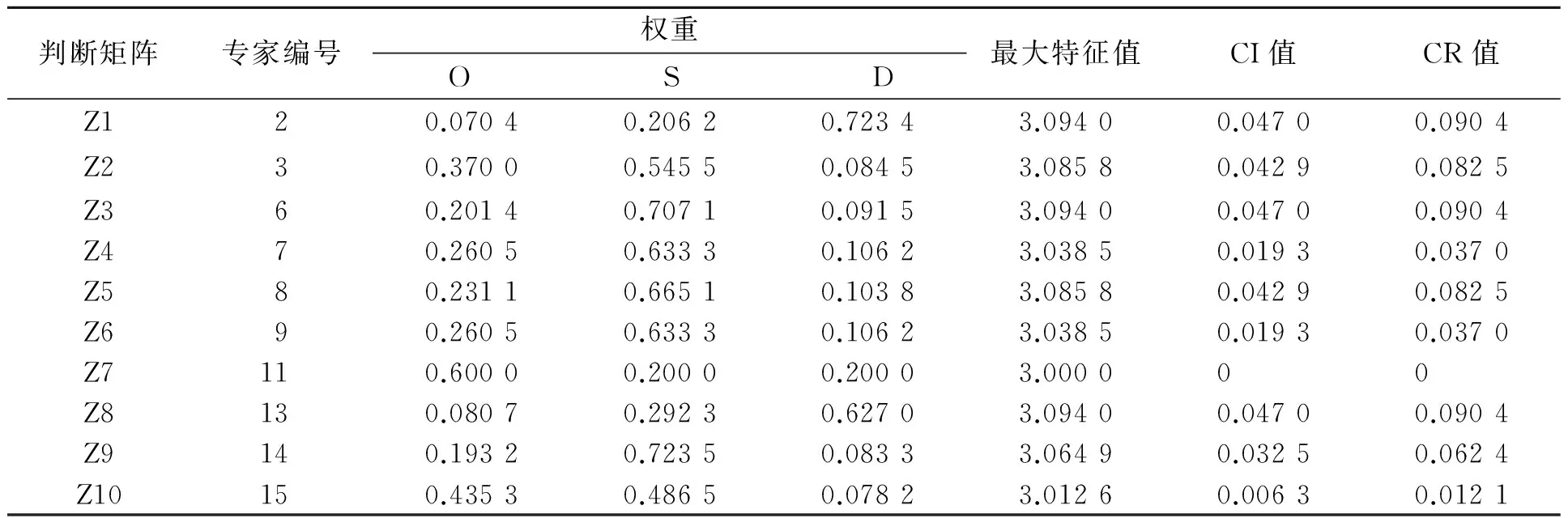
表5 专家评价指标的权重Tab.5 Weights of expert evaluation index

对专家进行分组：第1组是质量组，专家编号为2，3，共2人；第2组是工艺组，专家编号为6，共1人；第3组是生产组，专家编号为7，8，9，共3人；第4组是设计组，专家编号为11，共1人；第5组是技术管理组，专家编号为13，14，15，共3人.根据公式可以计算专家权重及相关参数，如表6所示.

表6 专家权重及相关参数Tab.6 Expert weights and related parameters

由表6最终可计算得到评价指标OSD的权重向量W=(0.2544 0.53 0.2156)T.

专家对各工序的失效模式进行模糊评价，可得到的等级评价矩阵，如表7所示.

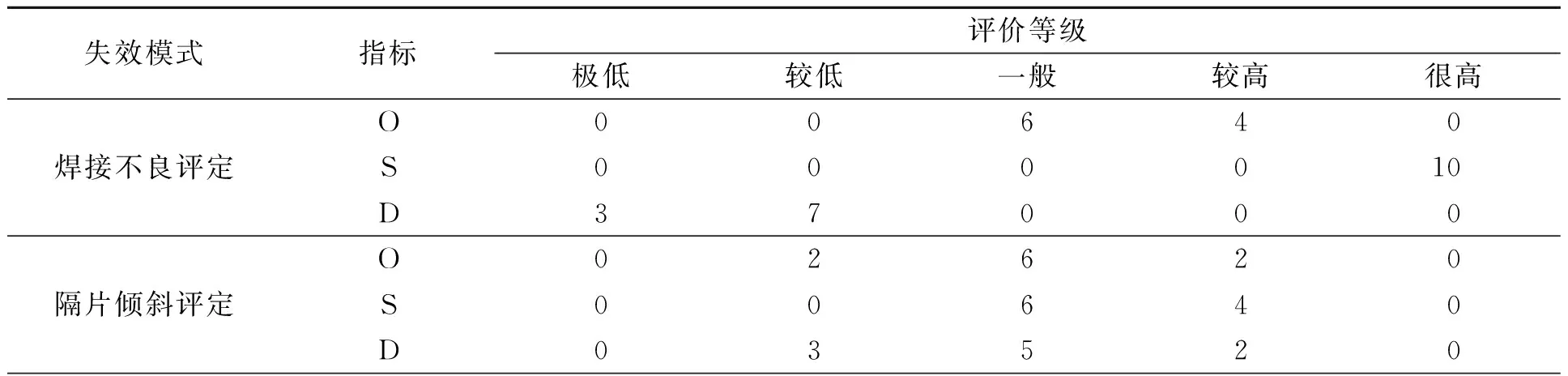
表7 等级评价矩阵Tab.7 Rating matrix

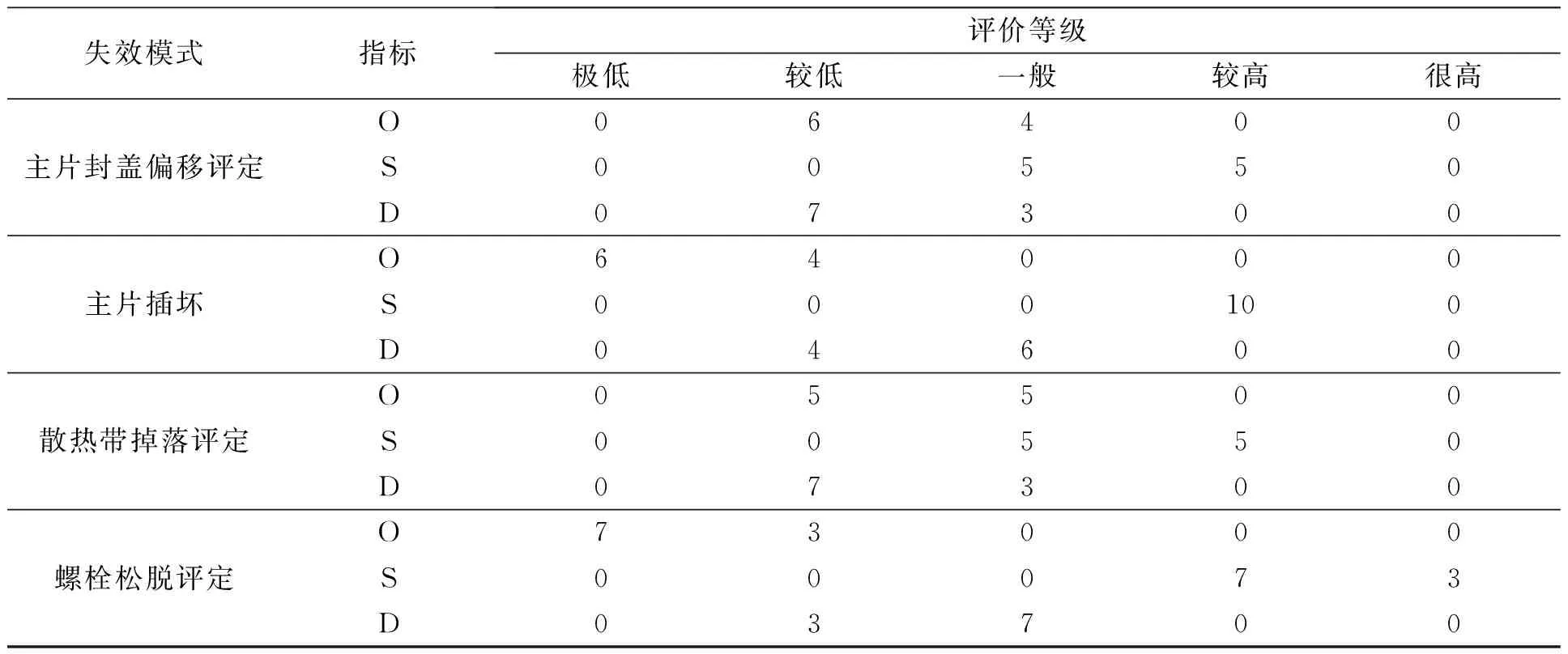
续表Continue table

统计各等级评分数量在评分总量上所占的比例，建立如下模糊评价矩阵为

根据公式可计算得到如下归一化后的模糊综合评价矩阵为

利用等级矩阵对以上模糊综合评价赋值，可计算得到最终的结论等级值，如表8所示.基于F-AHP的PFMEA方法和改进后的PFMEA方法分别得到的各工序风险顺序，如图1所示.

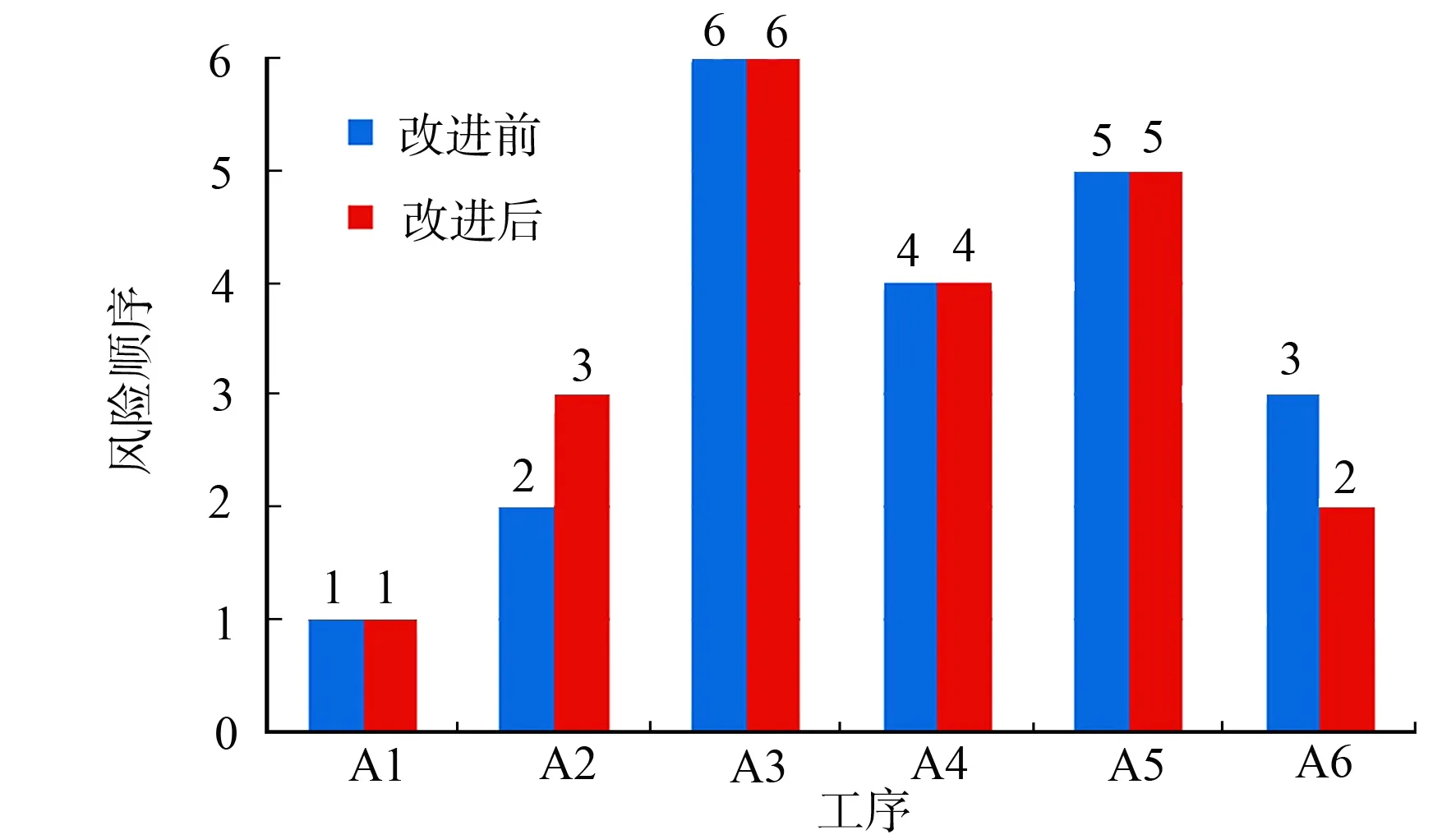
图1 改进前后PFMEA方法的结果比较Fig.1 Comparison of results before and after improvement of PFMEA method

表8 改进后的PFMEA结果Tab.8 Result of improved PFMEA

比较改进前后的PFMEA方法结果可知：风险顺序最靠前的都为A1(喷涂主片和封盖工序)，从钎焊式冷凝器的工艺来说，喷涂主片和封盖的工艺失效模式风险是极其重要的，符合实际情况；A2(插入隔片工序)和A6(最终装配工序)的风险等级发生了变化，经专家组的再次讨论分析确定A6工序装配的螺栓作为连接部件如果松脱后果更为严重的，所以相对于A2工序而言风险顺序应该更为靠前.因此，改进后的基于F-AHP的PFMEA方法更符合实际的产品要求.将改进PFMEA方法得到的结果按结论等级值从大到小进行排序，如表9所示.

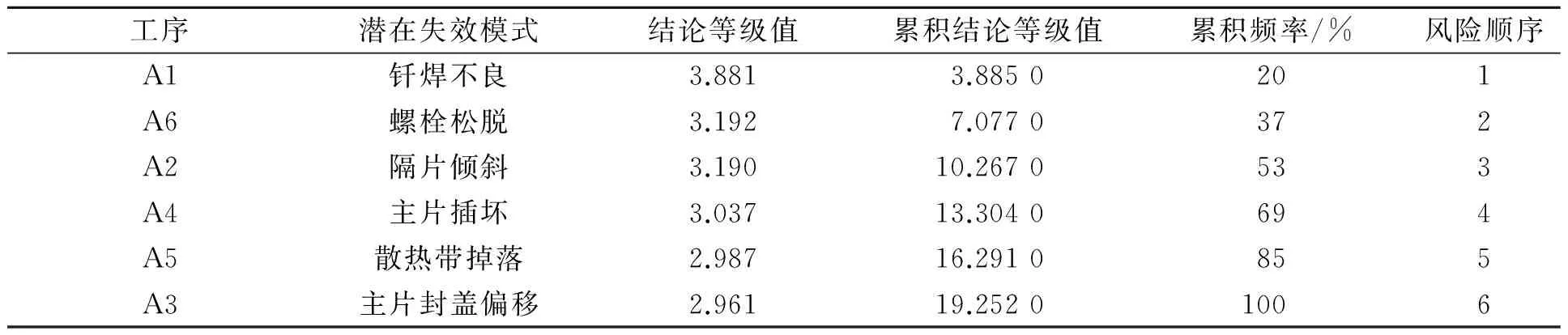
表9 改进后的PFMEA结果分析Tab.9 Result analysis of improved PFMEA

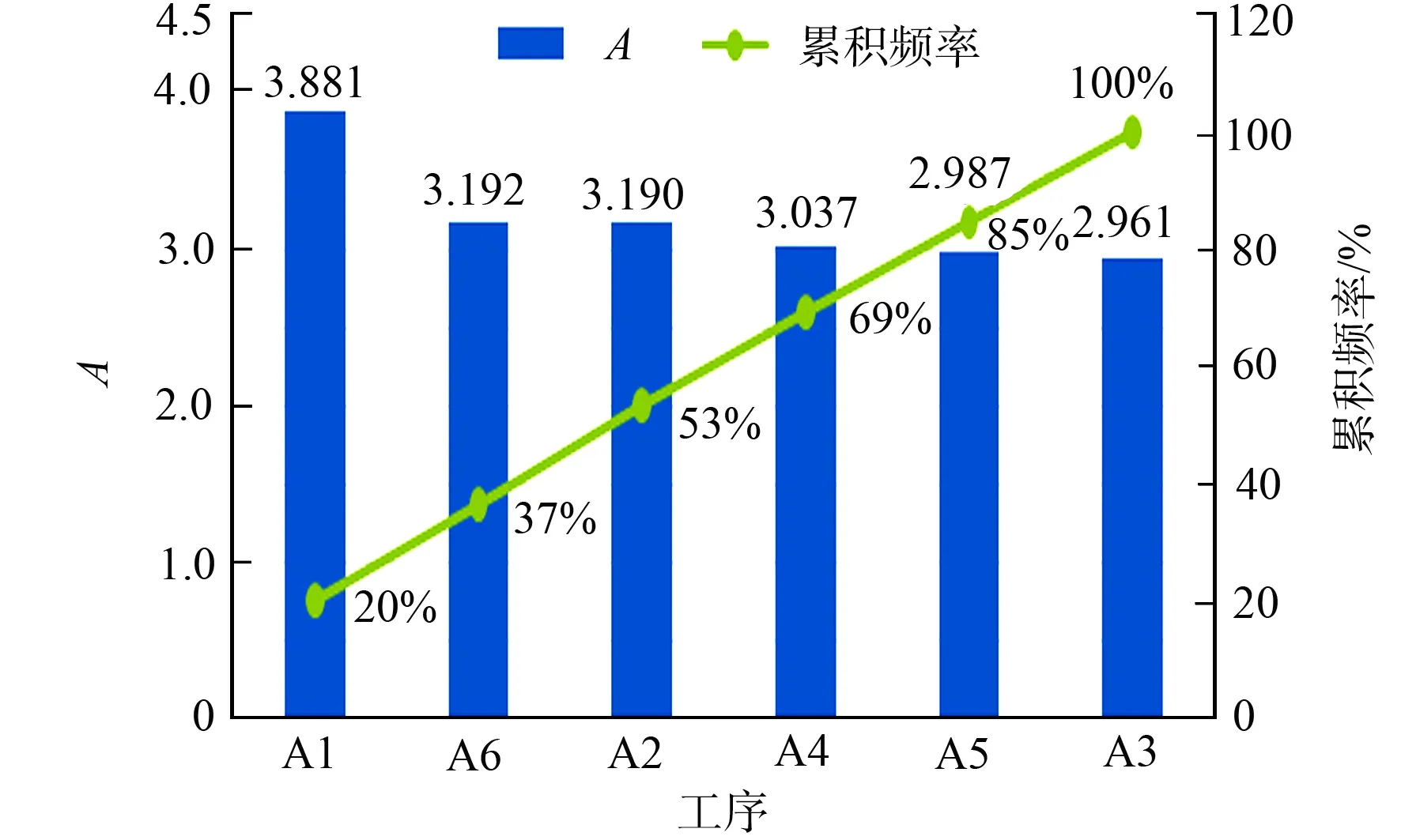
图2 产品失效的主要原因分析Fig.2 Analysis on main causes of product failure

进一步将表9结果绘制成帕累托图，如图2所示.由图2可知：A1，A6，A2和A4工序的失效占总失效频率的69%，是产品失效的主要原因，应当优先采取措施预防风险.

3 结束语

在传统基于模糊层次分析法的PFMEA方法基础上，通过实际应用分析，进一步考虑专家的个人区别和所属职业或岗位对失效风险排序的影响，构建专家判断矩阵变化程度和专家分组后组别容量对权重的影响程度两大参数;科学合理地设定专家权重，避免将专家均一化处理所造成的问题.所提方法在汽车空调冷凝器制造中开展实例应用研究，取得很好的效果.PFMEA法作为一个动态的改进工具，需要根据过程的评审、预计和改进不断地循环使用，持续改进.

[1] 门峰，姬升启.基于模糊集与灰色关联的改进FMEA方法[J].工业工程与管理，2008，13(2):55-59.

[2] 张得平.SHB公司PFMEA的应用及改进研究[D].上海:华东理工大学，2013.

[3] 孙璐璐，周晓军，奚立峰.基于FMEA的污水排放设备维护策略[J].工业工程与管理，2007，12(6):50-54.

[4] DINMOHAMMADI F，SHAFIEE M.A fuzzy-FMEA assessment approach for offshore wind turbines[J].International Journal of Prognostics and Health Management，2013，4(S2):59-68.

[5] SELLAPPAN N，PALANIKUMAR K.Modified prioritization methodology for risk priority number in failure mode and effect analysis[J].International Journal of Applied Science and Technology，2013，3(4):27-36.

[6] 盛精，王君，罗善明.采用模糊理论的零部件工艺PFMEA评估[J].华侨大学学报(自然科学版)，2015，36(6):609-614.

[7] BOWLES J B，PELAEZ C E.Fuzzy logic prioritization of failures in a system failure modes， effects and criticality analysis[J].Reliability Engineering and System Safety，1995，50(2):203-213.

[8] 杜晗恒，彭翀.基于模糊TOPSIS的FMEA方法[J].北京航空航天大学学报，2016，42(2):368-374.

[9] 王浩伦，徐翔斌，甘卫华.基于三角模糊软集的FMEA风险评估方法[J].计算机集成制造系统，2015，21(11):3054-3062.

[10] 安相华，于靖博，蔡卫国.基于混合多属性决策和关联分析的模糊粗糙FMEA评估方法[J].计算机集成制造系统，2016，22(11):2613-2621.

[11] 耿秀丽，张永政.基于犹豫模糊集的改进FMEA风险评估方法[J].计算机集成制造系统，2017，23(2):340-348.

(责任编辑： 陈志贤英文审校： 吴逢铁)

ImprovementandApplicationofPFMEAUsingFuzzyAnalyticHierarchyProcess

XIA Beixin1， CHEN Xin1， LI Long1， TAO Ningrong2， ZHANG Jiadong1

( 1. School of Mechatronics Engineering and Automation， Shanghai University， Shanghai 200072， China;2. College of Engineering， Shanghai Ocean University， Shanghai 201306， China)

In order to solve the problem that the risk ranking and the actual deviation of the expert judgment matrix are too homogeneous, an improved process failure mode and effect analysis (PFMEA) method based on fuzzy analytic hierarchy process is proposed in which expert weights are set taking into account individual differences and professions of experts. The extent of variation of expert judgment matrix is analyzed， and then experts are grouped and adjustments are made according to group sizes. The proposed method is validated through application examples of automobile air conditioning condenser manufacture. Research results show that compared with the existing method， the improved method can provide more accurate results when sorting the risks of failure modes.

automobile air conditioning condenser; product failure; process failure mode and effect analysis method； fuzzy analytic hierarchy process； expert weight

10.11830/ISSN.1000-5013.201611059

TH 162.1

A

1000-5013(2017)06-0868-07

2016-11-17

夏蓓鑫(1984-)，男，讲师， 博士，主要从事可靠性工程的研究.E-mail:3bxxia@shu.edu.cn.

国家自然科学基金资助项目(71401098)； 上海市高校青年教师培养资助计划(ZZSD15047)