基于编码Hash同态性的数据持有性证明方案

徐碧晗 郑 东 任 方

1.西安邮电大学 通信与信息工程学院，西安 710121 2.西安邮电大学 无线网络安全技术国家工程实验室，西安 710121

◎网络、通信与安全◎

基于编码Hash同态性的数据持有性证明方案

徐碧晗1，2，郑 东1，2，任 方1，2

1.西安邮电大学 通信与信息工程学院，西安 710121 2.西安邮电大学 无线网络安全技术国家工程实验室，西安 710121

为了保证用户在云存储服务器中数据的完整性，在分析已有数据持有性证明方案的基础上，提出了一种基于编码Hash同态性的数据持有性证明方案。通过将伪随机数与数据块进行“捆绑”作为标签来固定数据块位置，同时引进一种基于编码的Hash，并利用同态性来完成数据持有性验证。该方案的安全性依赖于译码的NP完全问题，可抵抗量子攻击，较传统的基于Hash同态性的数据持有性证明方案更难被攻破，同时通过理论分析，算法时间开销比以往方案更快，更有效。

数据完整性；数据持有性；编码Hash；同态性；标签；量子攻击

1 引言

近几年，随着IT设备计算量的增加，许多用户由于存储资源有限而选择将数据存储在远程云服务器中。远程服务器存储数据有很多好处，例如可以提供诸多服务：（1）消除了客户端存储开销和管理方面的压力；（2）相比客户端存储，可以提供高效性和可扩展性；（3）用户可以在任何时候、任何地方访问其数据。然而，无法确定远程云服务器在有敌手攻击的情况下或者服务器自身蓄意攻击的情况下（例如：服务器会删除用户不常用的数据来减少存储空间，从而把这些存储空间卖给其他用户），云服务器仍能正确存储用户数据。所以，为了使用户放心使用云存储服务，通过某种途径来验证数据是否完好地保存在服务器中是非常有必要的[1-2]，而且这种保证是必须的。然而，通常存储在云服务器中的外源数据文件是非常大的，所以用户为了检查所存储数据的完整性[3]而下载整个文件是不现实的，因为这样做所付出的开销和带宽与原来的目的背道而驰。

为了解决这一问题，一些学者们引入了远程数据完整性检测 RIC（Remote Integrity Checking）的概念[4-5]，即检测一些不可信的存储服务端是否能够避免数据的删除或篡改而正确的保存数据。RIC可以分为可证明数据持有 PDP（Provable Data Possession）方案[6-7]和可恢复证明POR（Proof Of Retrievability）方案[8]两种。远程数据完整性检验[9]最初由文献[4]提出，即应用基于RSA的Hash函数来计算整个数据的Hash值。如果用户将数据保存到一个不可信的云服务器中，PDP方案能够验证保存在服务器中数据的完整性，但是当数据被删除或者篡改时，PDP方案并不能够将数据恢复，而POR方案不仅能确保外源数据的私有性和完整性，还能够利用纠错码来恢复被改变过的数据。POR方案的概念在文献[8]中由Juels和Kaliski首次提出，在之后的研究中，学者们对POR方案进行了诸多改善，但其进展缓慢，相比PDP方案，研究力度较弱。自Ateniese等在文献[6]中对PDP方案进行了正式的定义以来，其研究团队首次提出多副本PDP方案即MR-PDP（Multiple-Replica）方案[10-11]。肖达等人[12]提出的有关数据完整性验证的文章，指出用户要求验证的数据块的位置以及个数，并发往服务器，服务器计算这些指定数据的Hash值发送给用户，用户将Hash值与校验块比较是否相等。Ateniese等人[13]提出了可扩展数据持有性证明SPDP（Scalable Provable Data Possession）方案，相比PDP方案增加了动态数据验证。之后由Erway等人[14]提出的动态数据持有性证明DPDP（Dynamic Provable Data Possession）方案允许动态数据的持有性验证。陈等人[15]利用同态Hash[16]给出了一种新的数据持有性证明方法HH-PDP（Homomorphic Hashing based Provable Data Possession）。随后李等人[17-18]提出了基于同态Hash的MR-PDP方案和一种动态数据的MR-PDP方案。现有的数据持有性证明方案都具备一定的安全性能，尽管如此，基于Shor算法[19]和Grover算法[20]等量子攻击仍对目前的数据持有性证明方案构成一定威胁，因此，能够有效抵抗量子攻击的数据持有性证明方案是很需要的。

黄等人[21]针对文献[15]中HH-PDP方案存在的问题进行了改善，然而该文章仍存在诸多不足。本文在文献[21]的基础上，结合文献[22-23]中的编码Hash和文献[15]中的Hash同态性引入了一种基于编码Hash同态性的数据持有性证明方法CHH-PDP（Coding Homomorphic Hashing based Provable Data Possession），该方案的安全性依赖于校验子译码SD（Syndrome Decoding）问题，该问题已被证明是NP完全问题，可以有效地抵抗目前已知的量子攻击，具有更高的安全性，同时运行效率良好，是一种更安全有效的数据持有性证明方案。

2 基础知识

2.1 数据持有性证明

数据持有性证明就是验证不可信的云存储服务器是否能够正确地保存数据，避免云存储服务器提供者非法删除或篡改数据。

用户将数据存储在云服务器中，如果没有相应的检测机制，当所存储的数据丢失或被伪造后，不能确保服务器能否及时将情况反映给用户，所以，用户需要随时知道存储在云服务器的数据是否完整并且随时可用。针对这一问题，学者们提出数据持有性证明，如果这一问题得到有效解决，云服务器将会广泛地被人所接受。用户将需要存储的数据进行一定预处理之后发送给云服务器进行存储，在任何时候用户都可以向云服务器提出挑战，云服务器向用户发送相关证据进行应答，用户利用证据来验证数据的完整性。数据持有性证明模型图如图1所示。

图1 数据持有性证明模型图

2.2 纠错码

纠错码的基本思想是在消息通过一个有噪信道传输前以多余符号的形式在消息中增加冗余度，这种冗余度是在一定的规则下添加的。编码后的消息在传输时可能还会遭受到信道中噪声的损害。在接收端，如果错误数在该码的设计限度内，则原始消息可以从受损的消息中恢复。对于纠错码的一些基本信息，下面给出如下几点定义：

定义1有限域Fq上的一个( )n,k线性分组码C是n维线性空间Fnq的一个k维子空间，Fnq中的向量称为字，而C中的向量称为码字，n称为码长，k称为码的维数。

定义2一个( )n,k线性分组码C的校验矩阵是一个( )

n-k×n的矩阵H。长为n的向量c是C的一个码字的充分必要条件是HcT=0。对于任意的字c，将HcT称为c的校验子。

定义3线性分组码的码字u=(u1,u2,…,un)的Hamming重量ω(u)定义为u与全0码字0的距离，即ω(u)=d(u ,0)，即非0位的个数。

2.3 Hash函数

典型的Hash函数是一个公开的函数，其作用是将任意长的消息映射成一个固定长度的摘要。具体构造过程是利用一个压缩函数F对给定的任意长消息进行多轮循环运算，最终得到的值为该任意长消息的Hash值。

如下给出循环迭代过程。假设该压缩函数的F输入为e位，输出为r位，且r＜e。

（1）首轮需要选择一个初始向量v0，长度为r，还需从源数据中选(e -r)位，与v0相连，形成长度为e的向量作为函数F的输入，输出r位。

（2）从第二轮开始，将前一轮输出的r位作为这一轮压缩函数F的输入，其余(e -r)位从源数据中选，计算出新的输出。

（3）重复循环第（2）步，直到源数据中所有数据都被取完为止。如果在最后一轮中，数据剩余位数少于(e -r)位，则任选若干比特将输入位填充到(e -r )位，函数最终的输出作为消息的Hash值。

具体迭代过程如图2所示。

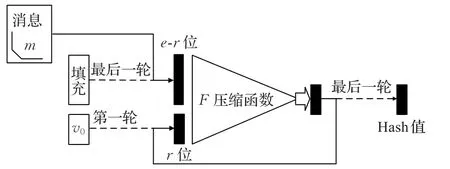
图2 Hash函数迭代过程

2.4 同态性

定义4群同态指的是群中一种保持结构不变的映射，两个群之间的映射 f：(A ;∗ )→(B ;⊙ )，如果满足B，则映射 f为群同态映射。

若定义4中A与B中的运算是加法，该式描述的是群之间的加法同态性；若A与B中的运算是乘法，则该式描述的是群之间的乘法同态性。两个群之间的同态映射原理如图3所示，A与B代表两个集合，g1,g2∈A，‘∗’代表 A中的运算，在集合 A中存在 g1∗g2=g′；而g1与g2的函数 f(g1),f(g2)∈B，‘⊙’代表B中的运算，即在集合B中存在 f(g1)⊙f(g2)=f(g ′)，而 f(g′)是g′的函数，满足 f(g1∗g2)=f(g1)⊙f(g2)，这便是集合A与B之间的同态性映射原理。

图3 同态性原理图

定义5对于具有两种运算的集合之间的映射 f：(A ;∗,·)→ (B ;⊙,⊗ )，若满足以下两个等式：

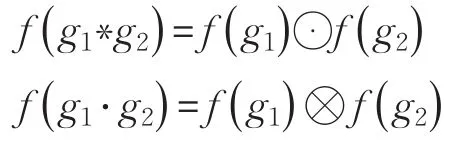
其中g1,g2∈A，f(g1),f(g2)∈B。则这两个集合在这两种运算下具有全同态性。

定义6群上的Hash函数h:{0 ,1}∗→{0 ,1}r，对于∀x1,x2∈{0 ,1}∗，都 有 h(x1∗x2)=h(x1)⊙h(x2)，其 中“∗”是定义在{0 ,1}∗上的群运算，“⊙”是定义在{0 ,1}r上的群运算，则该Hash函数具有群同态性，称为同态Hash。

2.5 校验子

定义7校验子译码SD（Syndrome Decoding）问题：输入有限域 Fq上的一个(n-k)×n的矩阵 H，向量s∈Fn-kq，整数k＞0，是否存在一个字 x∈Fnq，其重量w(x)≤k，使得 HxT=s。

3 基于编码的Hash函数

3.1 编码Hash的压缩函数

编码Hash函数的核心部分为压缩函数的构造，传统的编码Hash是基于传统压缩函数构造而成的。而利用校验子译码问题构造出的编码Hash具有特殊的内部结构，DanielAugot等在文献[22]中提出了编码Hash，且对该种编码Hash的内部结构进行了详细的讲解，本节将进行介绍，先引入正则字的定义。

定义8一个长度为n，重量为ω的字，把它平分为ω个等间距区间，如果这个字在每一个区间都仅有一个非0位，那么称这个字为( )n,ω正则字。

选择一个( )n,k纠错码，同时选择正整数ω，使得ω可以整除n，将所有长度为n的码字等分为ω个块，每块有该码的校验矩阵H是一个()n-k×n矩阵，同样将H等分为ω个子矩阵，H=(H1,H2,…,Hω)，子矩阵表示为Hi。压缩函数F定义为：，其中，则F的输入数据x∈Fe2。如下给出压缩函数的运算过程：

（1）将ebit输入数据x等分为ω个子块，即x1,x2,…,

xω，每个子块 xi包含

（2）将每个 xi转换为0到之间的整数xi。

（3）选择相应的子矩阵 Hi的第 xi+1列，表示为

（4）将选好的ω个列累加，获得一个长为r的比特串，就是F的输出，即计算

文献[23]中指出，以上得出的压缩函数F的输出相当于计算一个长为n，重为ω的正则字的校验子。利用压缩函数F可以构造出一个Hash函数，此时定义一个基于编码的Hash函数FH：{0 ,1}*→F2r，即对于任意长度的数据m，FH(m )都是一个长为n，重为ω的正则字c的校验子。即：

3.2 编码Hash的同态性

上述基于编码的Hash函数FH是具有同态性的，为此，假设所有(n ,ω )正则字构成的集合为G(n,ω)，在这个集合中定义一种循环右移函数RS(c)以及循环右移运算，用“⊕”来表示。其中RS(c)表示字符串c循环右移s位，如 R4(0 1000000)=(0 0000100)。以下将正则字中非0位默认为“1”。

（1）对于重量为w(a)=w(b)=1的正则字a,b，长为n，定义a⊕b=RSa(b)=RSb(a )。Sa 表示 a 中“1”左端“0”个数，同理 Sb表示b中“1”左端“0”的个数，c=a⊕b，则正则字 c中“1”左端“0”的个数为 (S a+Sb) modn。

（2）对于重量为w(a)=w(b)=ω的(n ,ω )正则字a,b。分别将a,b平分为 ω 块，a=(a1,a2,…,aω)，b=( )b1,b2,…,bω，每块 ai和 bi中含有位，且仅有一个“1”。按（1）中的方式将ai与对应位置的bi进行“⊕”运算，则 ai⊕bi=RSai(bi)=RSbi(ai)，其结果仍是只有一个“1”的位字符串，且“1”左端有()Sai+Sbimod个“0”。因此有：

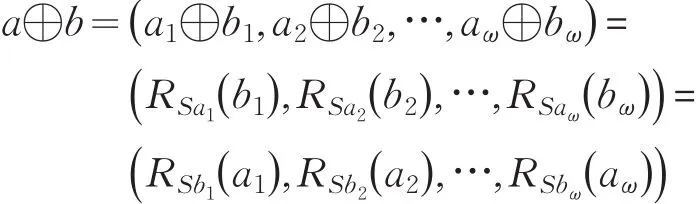
定理1基于编码的Hash函数FH是具有同态性的，假设所有(n ,ω )正则字构成的集合为G(n,ω)，如果该集合G(n,ω)在循环右移“⊕”运算下构成一个群，那么该称为一个正则字群。

证明 分别从正则字群所满足的四个条件入手。

①封闭性。假设正则字a,b∈G(n,ω)，分别将 a,b平分为ω块，每一个ai与bi分别仅有一个“1”，ai⊕bi的结果同样仅有一个“1”，故正则字a,b在“⊕”运算后仍属于正则字，满足封闭性。

②结合律。先将每一个(n ,ω )正则字a,b,d分为ω块，每一块分别进行验证。验证过程如下：

可得(ai⊕bi) ⊕di=ai⊕(bi⊕di) ，所以 (a⊕b)⊕d=a⊕(b⊕d)，满足结合律。

③存在单位元。假设码字a,e为G(n,ω)中的正则字，每一块为ai,ei。仅当Sei=0时，ai⊕ei=RSei(ai)=ai，此时的 ei中“1”左边没有“0”，即第一位是“1”，因此，码字e可以使得a⊕e=e⊕a=a。显然码字e是G(n,ω)中的单位元，故存在单位元。

④存在逆元。假设a是G(n,ω)中的正则字，e是G(n,ω)中的单位元。若想要等式ai⊕bi=ei成立，则必须满足，总能找到()n,ω 正则字b满足因此，正则字b可以使得a⊕b=e，则称b为a的逆元，即b=a-1，故存在逆元。

以上证明说明该(n,ω)正则字集合在“⊕”运算下确实可构成一个正则字群。由于上文中提到该编码Hash满足FH(m)=HcT，c为正则字，对于不同的输入数据 m1与 m2，FH(m1)=Hc1T，FH(m2)=Hc2T，则下式成立：

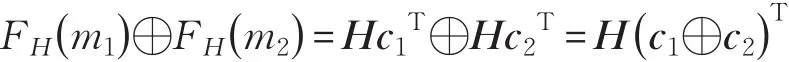
云服务器中存储数据时需要将数据M分为若干块进行存储，即M=(m1,m2,…,mB)，再将每一个二进制字符串mi作为Hash函数的输入来产生标签，最后需要利用同态性进行验证。定义mi之间的一种转换加法运算，用“∘”来表示，即将mi转换成十进制形式相加后取模，最后将其结果转换为二进制形式。如长为k的m1与 m2，转换加法表示为 m′=m1∘m2=Bin{(Dec(m1)+Dec(m2))mod2k}，其中 Dec(mi)代表将mi由二进制形式转换为十进制形式，Bin(mi)代表将mi由十进制形式转换为二进制形式。类似的很容易证明，mi在“∘”算法下构成一个群。

定理2基于编码的Hash函数FH：({ 0 ,1}∗;∘)→({ 0 ,1}r;⊕ )是群之间的一个同态Hash。

证明 由于上文推理出FH(m)=HcT，那么对于不同的数据块m1,m2有FH(m1)=Hc1T，FH(m2)=Hc2T。

令 m′=m∘m，则 F(m ∘m)=F(m ′ )=Hc′T，由

12H12H编码 Hash 的结构可得 出 c′=c1⊕c2，又 FH(m1)⊕F(m )=HcT⊕HcT=H(c ⊕c)T=Hc′T，则 F(m∘

H21212H1m2)=FH(m1)⊕FH(m2)。则该Hash函数具有群同态性，满足定义6中的公式，因此基于编码的Hash函数FH是同态Hash。

4 基于编码Hash的数据持有性证明

4.1 参数描述

方案中用到的参数说明如表1所示。

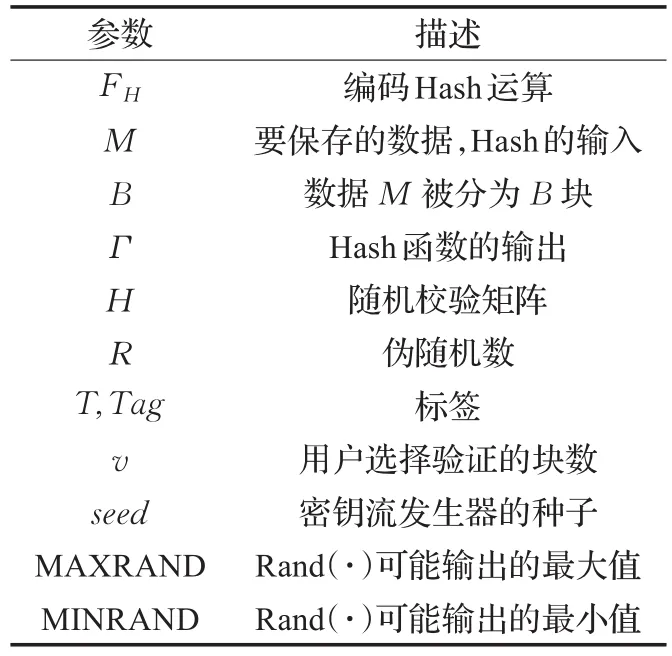
表1 参数描述

4.2 方案描述

基于编码Hash同态性的数据完整性证明分为五个阶段，即初始化（Setup）阶段，生成标签（TagBlock）阶段，挑战（Challenge）阶段，生成证据（ProofGen）阶段和验证证据（ProofVerify）阶段。CL与SR之间的数据传输图如图4所示。在进行Hash运算之前，先将数据M分为B块存储，之后若干阶段都以这些数据块为最小单位进行。

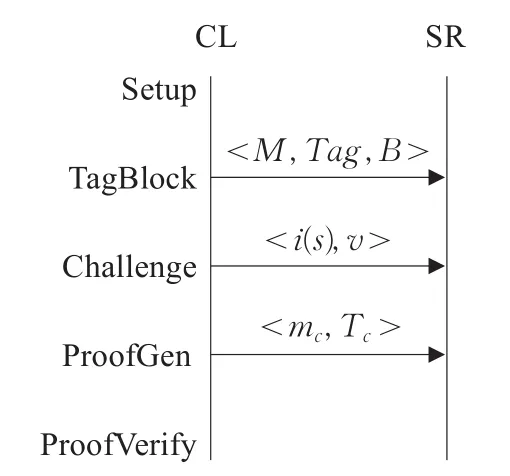
图4 数据传输流图

（1）Setup阶段：( )n,k,ω→FH

在该Setup阶段，生成一系列初始化参数，生成该纠错码的校验矩阵，生成编码Hash的运算结构FH（包括H），方便后面阶段的继续进行。

输入 n表示字的长度，k表示消息位的长度，ω为字的重量；

输出 编码Hash函数FH。

（2）TagBlock阶段

M=(m1,m2,…,mB)→ Tag=(T1,T2,…,TB)

客户端（CL）利用伪随机数生成器随机生成一系列(n ,ω ) 正则字 ci，计算 HcTi，从而得到伪随机数Ri=HcTi，将这些伪随机数与数据块的Hash值一对一的进行循环右移“⊕”运算，运算后的结果Ti作为标签。CL将消息M ，标签Tag，块数B，发送给云服务器（SR），自己保留Hash函数运算结构FH以及生成伪随机数时使用的种子seed。

输入 消息M=(m1,m2,…,mB)；

步骤 对于i∈(1,2,…,B)，有 Γi=FH(mi)；ci=rand(seed)；Ri=HcTi，则Ti=Γi⊕Ri；

输出Tag=(T1,T2,…,TB)。

（3）Challenge阶段

CL使用伪随机数生成器生成v个随机的挑战块，将其位置标号i(s)发送给SR，s∈{1 ,2,…,v}。

步骤 对于s∈(1,2,…,v)，计算：

（4）ProofGen阶段：(M,Tag,i(s),v)→(mc,Tc)

SR将v个随机挑战的数据块进行转换加法“∘”累加运算，结果记为mc；将v个随机挑战块的标签进行循环右移“⊕”累加运算，结果记为Tc；将mc和Tc的值返回给CL。

输入 消息M=(m1,m2,…,mB)，标签Tag等；

步骤 对于输入的消息M=(m1,m2,…,mB)，标签Tag ，计算

（5）ProofVerify阶段

CL利用自己保留的伪随机数生成器种子seed，重新生成伪随机数Ri(1)→Ri(v)，利用Hash函数的同态性，计算出 T′c值：

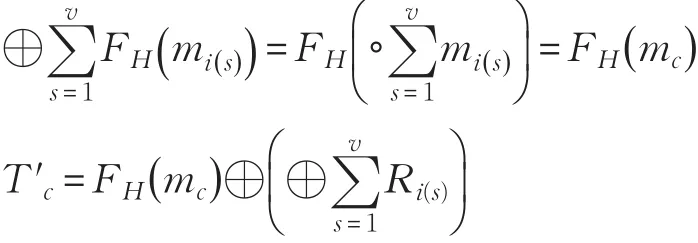
验证T′c=?Tc是否相同。若相同，则SR的数据持有正确。同时还可验证这个Tc是否对应正确的mc。

5 算法分析

下面主要对改进后的数据持有性证明算法，即基于编码Hash同态性的数据持有性证明CHH-PDP方案进行正确性、效率性和安全性分析，并与之前研究者们的HH-PDP方案进行对比。

5.1 正确性分析

下面来证明该方案的正确性，假设用户需委托云服务器保存的数据为M，将M 分为B块，M=(m1,m2,…,mB)，分别将每一个mi作为Hash函数FH的输入。输出相当于一个(n ,ω )正则字c的校验子，对于任意长度的输入数据mi，有FH(mi)=HcTi，FH(mi)有(n -k)bit。用户利用伪随机数生成器生成一系列(n ,ω )正则字ci，计算HcTi，得到伪随机数 Ri=HcTi，计算出标签Ti=FH(mi)⊕Ri，Tag=(T1,T2,…,TB)，然后用户将M，Tag，B发送给云服务器，自己保留FH算法（包括H）和伪随机数生成器种子seed。当用户想要验证任意v个数据块是否完整保存时，用户随机生成任意v个下标位置i(s)，将i(s)与检验块数v发送给云服务器。云服务器收到用户的挑战，计算出将证据(mc,Tc)返回给用户。用户利用seed重新生成要检验的v个伪随机数Ri(1)∼Ri(v)，同时利用云服务器发过来的mc，计算FH( )mc。由于编码Hash具有的同态性，所以，用户自己计算：

足以证明该算法的正确性。

5.2 效率分析

用户与服务器之间的“通话”存在于以下几个阶段：TagBlock阶段，用户将数据 M ，标签Tag，块数B，发送给服务器；当用户想要向服务器发出挑战时，即Challenge阶段，用户将想要检验的v个数据块下标发送给服务器；在ProofGen阶段，服务器将计算出的证据mc和Tc发送给用户进行回应。

方案中用户与服务器之间的每次“通话”，只需传输少量bit即可达到验证目的。经计算，假设用户选择使用( )

n,k纠错码的校验矩阵H来构造编码Hash，则每个标签块Ti仅占用( )n-kbit存储空间。在TagBlock阶段，用户发送给服务器的Tag仅占( )n-k×n个bit位；在ProofGen阶段，服务器返回给用户的Tc仅占( )n-k个bit位。

在文献[15]与文献[21]所用的由Krohn等[16]提出的Hash算法中，其Hash值长度取决于所选大素数 p的长度λp，例如，λp取典型值1 024 bit，则输入任意长数据块，Hash输出为1 024 bit。但是存在一个问题，算法安全性与λp的值成正比，与时间开销成反比，所以λp不宜太小。而本文算法中任意大小的输入数据块，编码Hash的输出都为(n -k)bit。所以该方案中编码Hash的输出大小取决于所选纠错码的校验子H的大小。取McElience经典参数，即 n=1 024，k=524，则编码Hash的输出大小为500 bit。通过对比，该方案中用户与服务器之间的“通话”所需的传输带宽更少，时间开销也更少，整个验证过程的效率有一定的提高。效率对比如表2所示。

表2 方案使用不同Hash的效率对比

为了更好地验证本方案的效率问题，在配置为Intel Core i7-5600U CPU 2.60 GHz，12 GB RAM的机器上基于由悉尼大学数学与统计学系计算代数学小组开发的功能强大的代数计算程序包Magma，版本Magma2_12-Windows，实现编码Hash函数算法。取n=8，k=5，ω=4，编码Hash的输入为一个任意长字符串（例如：100101011），输出为长度为3的字符串（001），显而易见该输出为一个正则字的校验子。并且构造出循环右移“⊕”算法，将两个正则字（001）与（010）进行“⊕”运算，输出结果为（100）。同时构造出转换加法“∘”，将长度为3的两个二进制字符串（110）与（100）进行“ ∘”运算，输出结果为（010）。通过实际测试，对一个20 kB的字符串计算其编码Hash的时间开销为0.17 s。

6 安全性分析

（1）算法安全性分析

服务器只知道标签Tag与块数B，不知道编码Hash函数FH的算法。服务器若想要欺骗用户，需知道Hash函数FH的算法，从而计算出每个数据块的Hash值Γi，利用Ti=Γi⊕Ri来得出伪随机数Ri，通过改变Ri来破坏数据持有性。由于在TagBlock阶段，用户并没有告知云服务器编码Hash函数FH的算法，所以服务器在知道标签Tag与块数B的条件下也无法求得伪随机数Ri，从而无法伪造标签来欺骗用户，增强了方案的安全性。

（2）编码Hash安全性分析

安全性方面，该方案最大的优点在于其核心部分使用的编码Hash的安全性依赖于这样一个NP完全问题，输入有限域 Fq上的一个(n-k)×n矩阵 H，向量s∈Fn-kq，整数k＞0，是否存在一个字 x∈Fnq，其重量w(x)≤k，使得 HxT=s。

文中得出结论，Hash函数FH的输出相当于计算一个( )

n,ω正则字的校验子。该校验子译码问题已经被证实属于NP完全问题，可有效抵抗目前的量子攻击，所以相比同类方案，该方案具有更高的安全。

7 结束语

本文提出的基于编码Hash的数据持有性证明CHH-PDP方案，是将纠错码的校验矩阵构造成Hash函数的形式，实现Hash的功能，并且利用编码Hash的同态性来验证云存储中数据的持有性。将编码Hash与前人方案相结合，使得数据持有性证明方案的运行效率与安全性得到提高。在将来的研究中，方案的冗余存储空间和时间开销与带宽消耗仍需进一步改进，从而实现更高效率的数据持有性证明。

[1]Wang H.Proxy provable data possession in public clouds[J].IEEE Transactions on Services Computing，2013，6（4）：551-559.

[2]Wang H.Identity-based distributed provable data possession in multicloud storage[J].IEEE Transactions on Services Computing，2015，8（2）：328-340.

[3]Liu C，Yang C，Zhang X，et al.External integrity verification for outsourced big data in cloud and IoT：A big picture[J].Future Generation Computer Systems，2015，49：58-67.

[4]Deswarte Y，Quisquater J J，Saïdane A.Remote integrity checking[M]//Integrity and Internal Control in Information Systems VI.Boston，MA：Springer，2003，140：1-11.

[5]Yu Y，Au M H，Mu Y，et al.Enhanced privacy of a remote data integrity-checking protocol for secure cloud storage[J].International Journal of Information Security，2015，14（4）：307-318.

[6]Ateniese G，Burns R，Curtmola R，et al.Provable data possession at untrusted stores[C]//Proceedings of the 14th ACM Conference on Computer and Communications Security，2007：598-609.

[7]Ren Y J，Shen J，Wang J，et al.Mutual verifiable provable data auditing in public cloud storage[J].网际网路技术学刊，2015，16（2）：317-323.

[8]Juels A，Kaliski Jr B S.PORs：Proofs of retrievability for large files[C]//Proceedings of the 14th ACM Conference on Computer and Communications Security，2007：584-597.

[9]Nguyen T C，Shen W，Luo Z，et al.Novel data integrity verification schemes in cloud storage[M]//Computer and information science.[S.l.]：Springer International Publishing，2015：115-125.

[10]Curtmola R，Khan O，Burns R，et al.MR-PDP：Multiplereplica provable data possession[C]//The 28th International Conference on Distributed Computing Systems，2008，ICDCS’08，2008：411-420.

[11]Balamurugan B，Mandadi A R，Mohan S，et al.Multiple replica based remote data possession checking scheme based on matrix representation of data[C]//International Confernce on Innovation Information in Computing Technologies，2015：1-5.

[12]肖达，舒继武，陈康，等.一个网络归档存储中实用的数据持有性检查方案[J].计算机研究与发展，2009，46（10）：1660-1668.

[13]Ateniese G，Di Pietro R，Mancini L V，et al.Scalable and efficientprovable data possession[C]//Proceedings of the 4th International Conference on Security and Privacy in Communication Networks，2008：1-10.

[14]Erway C C，Küpçü A，Papamanthou C，et al.Dynamic provable data possession[J].ACM Transactions on Information and System Security（TISSEC），2015，17（4）：15.

[15]陈兰香.一种基于同态 Hash的数据持有性证明方法[J].电子与信息学报，2011，33（9）：2199-2204.

[16]Krohn M N，Freedman M J，Mazieres D.On-the-fly verification of rateless erasure codes for efficient content distribution[C]//IEEE Symposium on Security and Privacy，2004：226-240.

[17]李超零，陈越，谭鹏许，等.基于同态hash的数据多副本持有性证明方案[J].计算机应用研究，2013，30（1）：265-269.

[18]李超零，陈越，余洋，等.一种动态数据多副本持有性证明方案[J].信息工程大学学报，2014，15（4）：385-392.

[19]Shor P W.Algorithms for quantum computation：Discrete logarithms and factoring[C]//Proceedings of the 35th Annual Symposium on Foundations of Computer Science，1994：124-134.

[20]Grover L K.A fast quantum mechanical algorithm for database search[C]//Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing，1996：212-219.

[21]黄石，刘文卓，曹天杰.改进的基于同态哈希的云存储数据完整性验证方案[J].河海大学学报：自然科学版，2015，43（3）.

[22]Augot D，Finiasz M，Sendrier N.A family of fast syndrome based cryptographic hash functions[C]//Dawson E，Vaudenay S.Progress in Cryptology-Mycrypt 2005.Berlin Heidelberg：Springer，2005：64-83.

[23]任方，郑东.一种基于编码的数字签名算法的改进[J].西安邮电大学学报，2015，20（4）：38-43.

XU Bihan1，2,ZHENG Dong1，2,REN Fang1，2

1.School of Communication and Information Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710121,China 2.National Engineering Laboratory for Wireless Security,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

Coding homomorphic hashing based provable data possession.Computer Engineering and Applications,2017,53（21）：91-97.

In order to verify the integrity of the data that users have stored in the storage server,based on analysis of existing Provable Data Possession（PDP）scheme and a homomorphic encoding hash function,this scheme puts forward a PDP solution.By pseudo-random number with the data block“bundling”as a tag to fix the position of the block,while the introduction of Hash function based on an encoding,this scheme also uses the homomorphic to complete data possession verification.The security of this scheme is dependent on NP-complete decoding against quantum attacks.It is more difficult to be broken than the traditional homomorphic hashing based PDP method.In theory,the algorithm scheme is more faster and effective.

data integrity;data possession;encoding Hash;the homomorphism;tag;quantum attack

A

TP309.2

10.3778/j.issn.1002-8331.1605-0092

国家自然科学基金（No.61272037，No.61472472）；陕西省自然科学基金（No.2015JQ6262）；陕西省教育厅专项科研项目（No.15JK1669）；西安邮电大学研究生创新基金（No.CXL2015-28）。

徐碧晗（1991—），女，硕士研究生，研究领域为信息安全，E-mail：xbh378698@163.com；郑东（1964—），男，博士，教授，研究领域为密码学，云存储安全；任方（1981—），男，博士，副教授，研究领域为密码学与信息安全。

2016-05-10

2016-09-19

1002-8331（2017）21-0091-07

CNKI网络优先出版：2016-12-02,http://www.cnki.net/kcms/detail/11.2127.TP.20161202.1503.026.html