广义犹豫模糊软集的相似度量及其应用
2017-11-28王艳平
黄 鹤,王艳平
辽宁工业大学 理学院,辽宁 锦州 121001
◎理论与研发◎
广义犹豫模糊软集的相似度量及其应用
黄 鹤,王艳平
辽宁工业大学 理学院,辽宁 锦州 121001
在广义模糊软集和犹豫模糊软集的基础上给出广义犹豫模糊软集的概念,并研究广义犹豫模糊软集的相似度量。首先利用三种犹豫模糊集合的包含度,构造犹豫模糊集间的相似度量公式。然后在犹豫模糊集相似度基础上给出广义犹豫模糊软集相似度量的公理化定义,并构造广义犹豫模糊软集的相似度量公式,这些公式可以计算参数集不同时两个广义犹豫模糊软集间的相似度。最后利用广义犹豫模糊软集相似度量方法构造了一种决策方法,并将这个决策方法应用于环境治理问题中。通过实例验证了所提出方法的可行性和有效性。
广义模糊软集;犹豫模糊软集;广义犹豫模糊软集;相似度量;包含度
1 引言
在现实世界中,事物之间的关系及其复杂,由于客观存在的随机性、模糊性及信息的不充分性,导致人们对事物的认识往往是不精确、不完全的,并具有一定的不确定性。1999年俄罗斯学者Molodtsov提出了软集[1-2]理论,该理论从参数化角度解决了不确定性问题,相较于概率论、模糊分析法、粗糙集等传统用于解决不确定性问题的数学工具,软集合理论具有自身独特的优势。目前,软集理论已经成功应用到运筹学、测度论、数据挖掘、洪水预测及文本分类等众多领域。近年来,学者们将软集的概念不断扩展,又相继提出了模糊软集[3]、直觉模糊软集[4]、犹豫模糊软集[5]、区间值模糊软集[6]、广义模糊软集[7]等理论。但到目前为止,还没有看到关于广义犹豫模糊软集的相关讨论,因此本文结合广义模糊软集和犹豫模糊软集给出广义犹豫模糊软集的概念。在软集理论中,如何合理地定义两个对象的相似程度,特别是模糊软集的相似性度量、距离度量以及这些不确定度量方法之间的关系得到了广泛关注。Majumdar与Samanta在文献[8-9]中对软集与模糊软集的不确定性度量进行了研究,并提出了一些不确定度量的方法,文献[7]给出了一种广义模糊软集的贴近度计算方法,改进了已知贴近度计算中的某些缺陷,文献[10]基于广义模糊软集在处理不确定性问题中的应用,对已有的贴近度进行了修正,并应用于医疗诊断中,取得了很好的效果。文献[11]基于模糊蕴含算子提出了一种新的模糊软集包含度与相似度量方法。文献[12]讨论了软直觉模糊集的相似测度、距离测度。这些成果开创了软集及其扩展模型的不确定性度量的研究,但仍有一些问题尚需进一步研究。因为无论模糊软集、广义模糊软集还是扩展的模糊软集,他们都是论域上参数化的子集族,不同的软集可能有不同的参数集。现有文献中大多数是针对参数集合相同的情况提出了各种扩展软集的相似度量,对参数集不相同时的相似度量讨论较少。因此,本文参考文献[13]对广义犹豫模糊软集的相似度量做了研究,给出了参数集不同时的广义犹豫模糊软集的相似度量公式,并给出了该公式在环境治理中的应用。
2 预备知识
本章首先在广义模糊软集和犹豫模糊软集的基础上给出广义犹豫模糊软集的定义,并定义空广义犹豫模糊软集和满广义犹豫模糊软集。
设初始论域为 U={x1,x2,…,xn},参数集为E={e1,e2,…,em}。
定义2.1设论域为U,集合A⊆E。F:A→HF(U)是一个映射,α是 A的一个犹豫模糊子集,即 Hα:A→{<e,Hα(e)>|e∈A},其中 Hα(e)为参数 e对应的犹豫模糊元。定义函数Fα:A→HF(U)×Hα(A),使∀e∈E ,Fα(e)=(F(e),Hα(e))。称 (Fα,A)为论域U 上的广义犹豫模糊软集(GHFS)。
定义2.2[14]设U为初始论域,定义空犹豫模糊集和满犹豫模糊集如下:
(1)空犹豫模糊集 Hφ:对∀x∈U ,Hφ(x)={0}。
(2)满犹豫模糊集HU:对∀x∈U ,HU(x)={1}。
由此给出两种特殊形式的广义犹豫模糊软集:
定义2.3(1)广义空犹豫模糊软集:对∀e∈E,Fα(e)=(Hφ,Hφ)。记为 Fφ。
(2)广义满犹豫模糊软集:对 ∀e∈E ,Fα(e)=(HU,HU)。记为FU。
为了解决参数集不同的情况,本文定义了广义犹豫模糊软集的扩充,这种方法可以使参数集不同的广义犹豫模糊软集扩充到相同的参数集下,使计算更简单更具一般性,后文会作出具体说明。
定义2.4初始论域U 上,集合 A⊆E,(Fα,A)为一个广义犹豫模糊软集,将 (Fα,A)扩充到 (,E),令:E→HF(U)×Hα(E),即对 ∀e∈E ,当 e∈A 时(e)=Fα(e),当 e∉ A 时,=(Hφ,Hφ)。则称,E)为(Fα,A)的扩充。
类似文献[7]中广义模糊软集的子集定义,不难得到广义犹豫模糊软集的子集定义。
定义2.5 设 A,B⊆E,(Fα,A)和(Gβ,B)是U 上的广义犹豫模糊软集。如果A⊆B,α是β的犹豫模糊子集,且∀e∈A,F(e)是G(e)的犹豫模糊子集,则称(Fα,A)是 (Gβ,B)的 广 义 犹 豫 模 糊 软 子 集 ,记 作(Fα,A)⊆(Gβ,B)。
特别的,当 (Fα,A)⊆(Gβ,B)且 (Gβ,B)⊆(Fα,A)时,称二者相等,记为:(Fα,A)=(Gβ,B)。
下面先回顾犹豫模糊集的包含度定义,然后给出犹豫模糊集合的几种包含度公式。
定义2.6[15]对任意的M ,N,Q∈HF(U),若映射D:HF(U)×HF(U)→[0,1]满足:
(1)0≤D(M/N)≤1
(2)M⊆N⇒D(M/N)=1
(3)M⊆N⊆Q⇒D(M/Q)≤D(M/N),D(M/Q)≤D(N/Q)
则称D为HF(U)上的包含度。
为了构造广义犹豫模糊软集的相似度量公式,这里先给出几个犹豫模糊集合间的包含度公式。设U为论域,M,N为U上的两个犹豫模糊集合,hM(xi)和hN(xi)(i=1,2,…,n)分别表示两个集合的犹豫模糊元,则有:



均为犹豫模糊集的包含度。其中包含度D1是将犹豫模糊集合退化成一般模糊集合来计算包含度,D2,D3
[16]是将犹豫模糊集合退化成区间值模糊集合来计算包含度。
3 犹豫模糊集合间的相似度量
相似度描述了集合之间的接近程度,模糊集和软集的相似度量已经广泛应用于各个领域。为方便下一章讨论广义犹豫模糊软集的相似度量,本章先给出犹豫模糊集合间相似度的公理化定义,然后基于犹豫模糊集的包含度构造相似度公式并给出证明。
定义3.1设U为论域,HF(U)表示论域上所有的犹豫模糊集合,映射

对论域上任意的犹豫模糊集合M,N,K满足:
(3)若M⊆N⊆K,则有

则称映射Sˉ为犹豫模糊集合的相似度。
(2)对论域上任意的犹豫模糊集合M,N,K有:

因为 Di(N/K)≤1,Di(K/N)≤1,所以min{Di(N/K),Di(K/N)}≤ 1 ,因此得证。
(3)若M⊆N⊆K,则有
Di(K/M)≤Di(K/N)
Di(K/M)≤Di(N/M)
所以

4 广义犹豫模糊软集的相似度量
根据上一章犹豫模糊集合间相似度,本章定义广义犹豫模糊软集的相似度如下:
定义4.1设U为论域,E为参数集,GHFS(U,E)为论域(U,E)上所有的广义犹豫模糊软集,对论域(U,E)上任意的广义犹豫模糊软集 (Fα,A),(Gβ,B),(Pγ,C),映射 SG:GHFS(U,E)×GHFS(U,E)→[0,1],满足:
(1)SG((Fα,A),(Gβ,B))=SG((Gβ,B),(Fα,A))
(2)SG((Fα,A),(Fα,A))≥maxSG((Gβ,B),(Pγ,C))
(3)若 (Fα,A)⊆(Gβ,B)⊆(Pγ,C),则有
SG((Fα,A),(Pγ,C))≤ min(SG((Fα,A),(Gβ,B)),SG((Gβ,B),(Pγ,C)))
则称映射SG为广义犹豫模糊软集的相似度量。
设U为论域,E为参数集。令A⋃B=E′,E′⊆E,(Fα,A)和(Gβ,B)为参数集不同的广义犹豫模糊软集。为了便于计算,利用定义2.4将(Fα,A)和(Gβ,B)扩充成
定理4.1广义犹豫模糊软集的相似度量公式为:

其中,F(ej)={hF(x1j),hF(x2j),…,hF(xnj)},G(ej)={hG(x1j),hG(x2j),…,hG(xnj)},(ej∈A⋃B)。
证明(1)显然成立;
(2)对于广义犹豫模糊软集 (Fα,A),(Gβ,B)和(Pγ,C),有

对于 (Gβ,B)和(Pγ,C),有

所以,maxSGi((Gβ,B),(Pγ,C))≤1。
(3) 对于 (Fα,A),(Gβ,B)和 (Pγ,C),若 (Fα,A)⊆(Gβ,B)⊆(Pγ,C),根据定义2.4,有 F(ej)⊆G(ej)⊆P(ej),Hα(ej)⊆ Hβ(ej)⊆ Hγ(ej)。
显然有:

所以必然有:
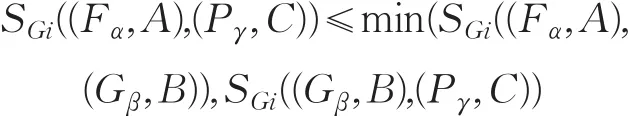
得证。
5 广义犹豫模糊软集的相似度量在环境治理中的应用
在本章,给出一个应用实例[17],说明如何应用广义犹豫模糊软集的相似度量解决环境治理中的决策问题。
某省需要治理几个城市环境污染,需要对每个城市污染严重程度进行比较,从而合理地分配所需事宜。设论域U={x1,x2,x3}分别代表市区、乡村和野外。将国家环境调查报告指出的几大污染看做参数集E={e1,e2,e3,e4},其中ei(i=1,2,3,4)分别代表:“大气污染”,“水体污染”,“土壤污染”,“生态污染”。该省有 A、B、C三个城市需要治理。
该如何决定治理环境的先后可通过以下步骤进行决策:
步骤1考虑施工难度、资金调度等实际情况,专家给出理想方案所对应的标准广义犹豫模糊软集。
步骤2通过调查问卷、实地考察等手段对A、B、C三个城市各种污染程度进行量化评估得到相应的广义犹豫模糊软集。
步骤3分别计算各城市所对应的广义犹豫模糊软集与标准广义犹豫模糊软集的相似度。
步骤4相似度越大,说明治理这个城市的环境可以达到最佳治理效果,以此作出决策。
专家给出理想方案及三个城市的调查结果如表1~4。

表1 理想方案

表2 A城市污染程度

表3 B城市污染程度

表4 C城市污染程度
根据表1~4,可得到相应的广义犹豫模糊软集:


计算广义犹豫模糊软集相似度:

因为 SG1((Pγ,C),(Zδ,E))>SG1((Gβ,B),(Zδ,E))>SG1((Fα,A),(Zδ,E)),所以该省治理C城市的污染回答道最佳治理效果。
通过定义2.4将上述四个广义犹豫模糊软集扩充为参数集为{e1,e2,e3,e4}的广义犹豫模糊软集,然后首先采用犹豫模糊集包含度公式:
同理,当采用D2(N/M)和D3(N/M)为犹豫模糊集合包含度计算广义犹豫模糊软集相似度量时,也可得出相应的相似度如下:

同样可以通过 SGi((Pγ,C),(Zδ,E))> SGi((Gβ,B),(Zδ,E))> SGi((Fα,A),(Zδ,E))(i=2,3)得到最佳决策结果为C城市。
6 总结
本文首先结合广义模糊软集与犹豫模糊软集理论,定义了广义犹豫模糊软集。然后利用犹豫模糊集合的包含度公式,讨论了犹豫模糊集合的相似度量,进而给出了广义犹豫模糊软集相似度量的公理化定义及公式。由于包含度和相似度的公理化定义及公式可以有多种不同形式,因此本文只是提供了一种一般的构造方法,基于此种方法还可以得到其他不同形式的相似度公式。此外,文中给出了一种应用广义犹豫模糊软集相似度解决实际问题的决策方法,这只是广义犹豫模糊软集相似度的一种最简单的应用。当然还可以将其应用到广义犹豫模糊软集的聚类分析、综合评判等实际问题中。
[1]Molodtsov D.Soft set theory-first results[J].Computers Mathematics with Applications,1999,37(4/5):19-31.
[2]Molodtsov D.The theory of soft sets[J].Moscow(in Russian):URSS Publishers,2004.
[3]Maji P K,Biswas R,Roy A R.Fuzzy soft sets[J].The Jurnal of Fuzzy Mathematics,2001,9(3):589-602.
[4]Maji P K,Biswas R,Roy A R.Intuitionistic fuzzy soft sets[J].Journal of Fuzzy Mathematics,2001,9:677-691.
[5]Wen Xi.Hesitant fuzzy soft sets[J].Computer Engineering and Applications,2015,51(24):56-60.
[6]Guo Zhilian,Yang Hailong.Lattice structures of intervalvalued fuzzy soft sets[J].Computer Engineering and Applications,2011,47(33):7-9.
[7]Majumdar P,Samanta S K.Generalised fuzzy soft sets[J].Computers and Mathematics with Applications,2010,59(4):1425-1432.
[8]Majumdar P,Samanta S K.Similarity measure of softsets[J].New Mathematics and Natural Computation,2008,4(1):1-12.
[9]Majumdar P,Samanta S K.On similarity measures of fuzzy soft sets[J].International Journal of Advance in Soft Computing and Its Application,2011,3(2):1-8.
[10]李红霞.改进的广义模糊软集的贴近度[J].佳木斯大学学报,2014,32(6):944-947.
[11]洪智勇.模糊软集之间的相似性度量及应用[J].计算机工程与应用,2015,51(12):16-20.
[12]刘雅雅,秦克云,陈明奎.软直觉模糊集的相似、距离和熵测度[J].济南大学学报,2015,29(6):414-419.
[13]Wang Chang,Qu Anjing.The applications of vague soft sets and generalized vague soft sets[J].Acta Mathematicae Applicatae Sinica English,2015,31(4):977-990.
[14]Torra V.Hesitant fuzzy sets[J].International Journal of Intelligent Systems,2010,25(6):529-539.
[15]王昌.Vague软集的相似度量及其应用[J].统计与决策,2012(2):77-79.
[16]王金英,王艳平,韩晓冰.基于包含度的犹豫模糊属性约简[J].井冈山大学学报:自然科学版,2016,37(2):9-13.
[17]周小强.软集与犹豫模糊集理论及其在决策中的应用[D].长沙:湖南大学,2014.
HUANG He,WANG Yanping
College of Science,Liaoning University of Technology,Jinzhou,Liaoning 121001,China
Similarity measures of generalized hesitant fuzzy soft sets and its application.Computer Engineering and Applications,2017,53(21):37-41.
The concept of generalized hesitant fuzzy soft set is proposed based on the generalized fuzzy soft set and hesitant fuzzy soft set in this paper,and the similarity measure of the generalized hesitant fuzzy soft sets is discussed.At first,the similarity measure formula of hesitant fuzzy set is constructed by using three kinds of inclusion degree of hesitant fuzzy sets.Then the axiomatic definition of similarity measures of the generalized hesitant fuzzy soft set is provided based on hesitant fuzzy set similarity measure,and similarity measure formula of the generalized hesitant fuzzy soft set is constructed.The similarity measure of generalized hesitant fuzzy soft sets with different parameter sets can be calculated by using these formulas.Finally,a decision method is constructed by using the similarity measurement of generalized hesitant fuzzy soft set,and the decision-making method is applied to the problems of environmental governance.It can be verified the feasibility and effectiveness of the proposed method.
generalized fuzzy soft set;hesitant fuzzy soft set;generalized hesitant fuzzy soft set;similarity measures;inclusion degrees
A
TP311
10.3778/j.issn.1002-8331.1606-0164
国家自然科学基金(No.61473139)。
黄鹤(1991—),男,硕士研究生,研究领域为粗糙集理论及其应用;王艳平(1965—),女,教授,研究领域为模糊集与粗糙集,E-mail:lxywyp@lnut.edu.cn。
2016-06-12
2016-08-15
1002-8331(2017)21-0037-05
CNKI网络优先出版:2016-11-21,http://www.cnki.net/kcms/detail/11.2127.TP.20161121.2049.084.html
