电力网络的谐振稳定性分析方法研究

徐政，王世佳，邢法财，肖晃庆

(浙江大学电气工程学院，杭州市 310027)

电力网络的谐振稳定性分析方法研究

徐政，王世佳，邢法财，肖晃庆

(浙江大学电气工程学院，杭州市 310027)

随着电力系统电力电子化程度的不断加深，近年来出现了多起机理不明的新的振荡现象。提出了电力网络谐振稳定性的概念，试图将上述机理不明的振荡现象纳入到电力网络的谐振不稳定范畴，从而基于线性网络理论对众多复杂振荡现象进行分析，为借助数学上完全成熟的线性系统理论解决电力系统实际问题提供一条途径。围绕判断谐振稳定性的分析方法展开，通过引入电力网络的s域节点导纳矩阵，将电力网络的谐振稳定性问题归结为判断s域节点导纳矩阵行列式的零点在复平面上的分布问题。首先，理论证明了s域节点导纳矩阵行列式的零点就是系统的特征值。其次，给出了求解s域节点导纳矩阵行列式零点的实部-虚部交叉迭代法。接着，推导了特定谐振模式下的节点电压振型和参与因子矩阵，这2个指标可用来定位特定谐振模式发生的位置。最后，通过算例展示了所提方法在分析电力网络谐振稳定性方面的有效性。

电力网络；状态空间模型；s域节点导纳矩阵；谐振模式；谐振稳定性；节点电压振型；参与因子矩阵

0 引 言

振荡是电力系统运行过程中的一种常见现象[1-2]。一般来说，电力系统振荡可以分为3种类型：(1)发电机轴系的振荡(扭振)；(2)发电机转子之间的振荡；(3)电力网络内部的固有谐振。随着大量电力电子装置接入电力系统，电力网络的固有谐振问题变得更加严重和复杂。由于某些电力电子装置在一定的频段内存在负电阻效应，使得原先谐振稳定的电力网络有可能变得谐振不稳定，从而造成严重的后果。例如，2011年至今，河北沽源地区的双馈风电场与其电容串补装置相互作用，引发了上百次频率为 3～10 Hz的次同步振荡，造成变压器异常振动和大量风机脱网[3]。福建厦门柔性直流输电工程在直流侧出现过次同步振荡问题，该振荡现象为非衰减和非等幅振荡，振荡频率为25 Hz左右[4]。新疆哈密“7·1”直驱风机引起的火电机组次同步振荡事件[5]，可以认为是由电力网络谐振与发电机轴系扭振相互作用而导致的机网复合共振问题。

当电力网络发生谐振时，很容易引起系统的过电压、过电流，甚至会与发电机轴系扭振相互作用而导致机网复合共振，威胁电力系统的安全稳定运行。因此，亟需对电力网络的固有谐振结构和谐振稳定性进行透彻的研究。

本文深入研究基于s域节点导纳矩阵Y(s)的电力网络谐振稳定性分析方法。首先，在理论上论证s域节点导纳矩阵Y(s)行列式为0的根就是系统的特征值，并用一个简单算例进行了验证。其次，提出一种实部-虚部交叉迭代的方法，用以确定s域节点导纳矩阵Y(s)行列式为0的根的位置；这种求解方法与采用Newton-Raphson法迭代求解det[Y(s)]零点的方法相比，可以大幅度减少计算量。接着，推导特定谐振模式下的节点电压振型和参与因子矩阵，这2个指标可用来定位特定谐振模式发生的位置。最后，通过IEEE次同步谐振第一标准测试系统和IEEE 39节点测试系统，展示对实际电网进行谐振稳定性分析的结果。

1 理论基础

1.1 谐振稳定性的定义

当考虑输电线路等分布参数元件时，因描述分布参数元件特性的方程是偏微分方程，整个电力网络已不能用线性定常系统的标准状态空间模型来描述。另外，若进一步考虑元件参数随频率而变化的特性，那么即使对于由集总参数元件构成的电力网络，也无法用线性定常系统的标准状态空间模型来描述。因此，当电力网络包含分布参数元件和频变参数元件时，所谓的电力网络谐振稳定性该如何定义就成为一个重要问题。

1999年，文献[7]首先提出了采用s域节点导纳矩阵Y(s)来分析复杂电力网络小信号稳定性的概念和方法，这里所谓的“复杂电力网络小信号稳定性”本质上与本文所称的“电力网络谐振稳定性”相一致。因此，对于包含分布参数元件和频变参数元件的复杂电力网络，谐振稳定性的概念将基于s域节点导纳矩阵Y(s)来定义。2001年，文献[8]对采用s域节点导纳矩阵Y(s)进行小信号稳定性分析的方法做了进一步的发展和完善。其要点如下：(1)所谓的“s域节点导纳矩阵Y(s)”，国内也称为“运算导纳矩阵”，是早已存在的概念；例如，电容C的运算导纳是sC，电感L的运算导纳是1/(sL)；简单地说，将交流稳态分析时元件导纳模型中的j用s来替换就构成了对应元件的运算导纳，对于分布参数的输电线路，也有类似的结果[8]；在得到各元件的运算导纳模型后，构建运算导纳矩阵的步骤与交流稳态分析时构建节点导纳矩阵的步骤完全一致。(2)对于包含分布参数元件和频变参数元件的电力网络，构建其s域节点导纳矩阵Y(s)并不存在特殊困难；因而对于一般性的电力网络，基于s域节点导纳矩阵Y(s)分析其谐振稳定性具有普遍的适用性。(3)令Y(s)的行列式为det[Y(s)]，那么det[Y(s)]=0的根(以下统称为det[Y(s)]的零点)就是该电力网络的谐振模式，det[Y(s)]的所有零点就是该电力网络的所有谐振模式，如果det[Y(s)]的所有零点都位于复平面的左半平面，那么该电力网络就是谐振稳定的。容易证明，包含分布参数元件的电力网络，其谐振模式有无限个。

由上面的介绍可知，判断电力网络谐振稳定性与判断det[Y(s)]的所有零点是否都位于复平面的左半平面等价。因此，判断电力网络谐振稳定性的最直接方法就是求出det[Y(s)]的所有零点，或者求出det[Y(s)]在指定频段内的所有零点。更进一步，可以对电力网络的谐振结构进行分析，电力网络的谐振结构包含4方面的信息：(1)电力网络在分析的频段内存在哪些固有谐振模式；(2)各谐振模式的频率；(3)各谐振模式的阻尼；(4)各谐振模式的振型。文献[8]提出了采用Newton-Raphson法迭代求解det[Y(s)]零点的方法。该方法需要同时建立2个s域节点导纳矩阵，一个是Y(s)，一个是Y(s)关于s的导数矩阵dY(s)/ds，计算量比较大。

1.2 系统特征值的定义

电力网络的动态特性可以通过KVL电压方程、KCL电流方程和储能元件动态特性方程进行描述；其中前2类方程为代数方程，后1类方程为一阶微分方程。当电力网络由集总参数元件构成，且元件参数不随频率变化时，根据上述3类方程可以列写出单输入单输出系统如下的状态空间模型[9-10]：

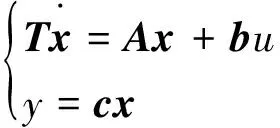
(1)

式中：{A,T}共同构成状态空间的系统矩阵；x为状态变量向量，包括储能元件状态(电容电压、电感电流等)；输出y为第k个节点的电压；输入u为第j个节点的注入电流；b是一维常数列向量；c是一维常数行向量。

对式(1)进行拉氏变换，有

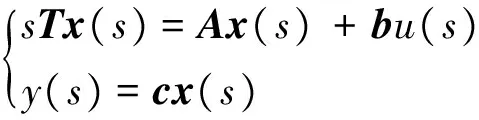
(2)

因此s域下转移阻抗zkj(s)的表达式为

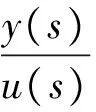
(3)

式中：分母det(sT-A)表示矩阵sT-A的行列式，“*”表示相应矩阵的伴随矩阵。根据线性代数的基本理论可知，det(sT-A)是系统的特征多项式，det(sT-A)=0的根是系统的特征值。系统特征值对应于电力网络的所有谐振模式；当特征值都位于复平面的左半平面时，该电力网络就是谐振稳定的。由于状态空间模型需要在集总参数元件的条件下列写，此时谐振模式为有限个。

1.3 基于s域节点导纳矩阵求取特征值

除状态空间模型外，可以采用s域节点导纳矩阵分析系统特征值[7-8]。s域下系统节点电压方程为

Y(s)Vnode(s)=Inode(s)

(4)

式中：Y(s)为s域下的节点导纳矩阵；Vnode(s)和Inode(s)分别为s域下的节点电压向量和节点注入电流向量。同样考虑单输入单输出系统，设在节点j上的注入电流为ij(s)，在节点k上的输出电压为vk(s)。则方程(4)可以写成如下形式：

(5)

这里b′是一维列向量，其第j个元素为1，其余元素为0；而c′是一维行向量，其第k个元素为1，其余元素为0。因此s域下转移阻抗zkj(s)的表达式为

(6)

式中：det[Y(s)]为Y(s)的行列式；Y(s)*为Y(s)的伴随矩阵。

由于Y(s)的元素不一定都是s的多项式，例如对于电感元件L，其运算导纳的表达式是1/(sL)，因此通过对det[Y(s)]外乘s的幂函数sm(m为正整数)，一定能够将det[Y(s)]化成s的多项式。对比式(3)和式(6)，det(sT-A)与smdet[Y(s)]都是系统的特征多项式。这样，在s≠0的条件下，det(sT-A)=0与det[Y(s)]=0的根是完全一致的。因此，det[Y(s)]=0的非零根一定是系统的特征值，从而论证了采用状态空间法和s域节点导纳矩阵法在求取系统特征值上具有一致性。

值得指出的是，在构建s域节点导纳矩阵Y(s)时，并不要求网络元件使用集总参数模型。因此对于一般性的电力网络(包括分布参数元件和频变参数元件)，相对于状态空间法，基于s域节点导纳矩阵分析谐振稳定性具有更为普遍的适用性。容易证明，包含分布参数元件的电力网络，其谐振模式有无限个。

1.4 实例验证

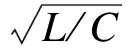
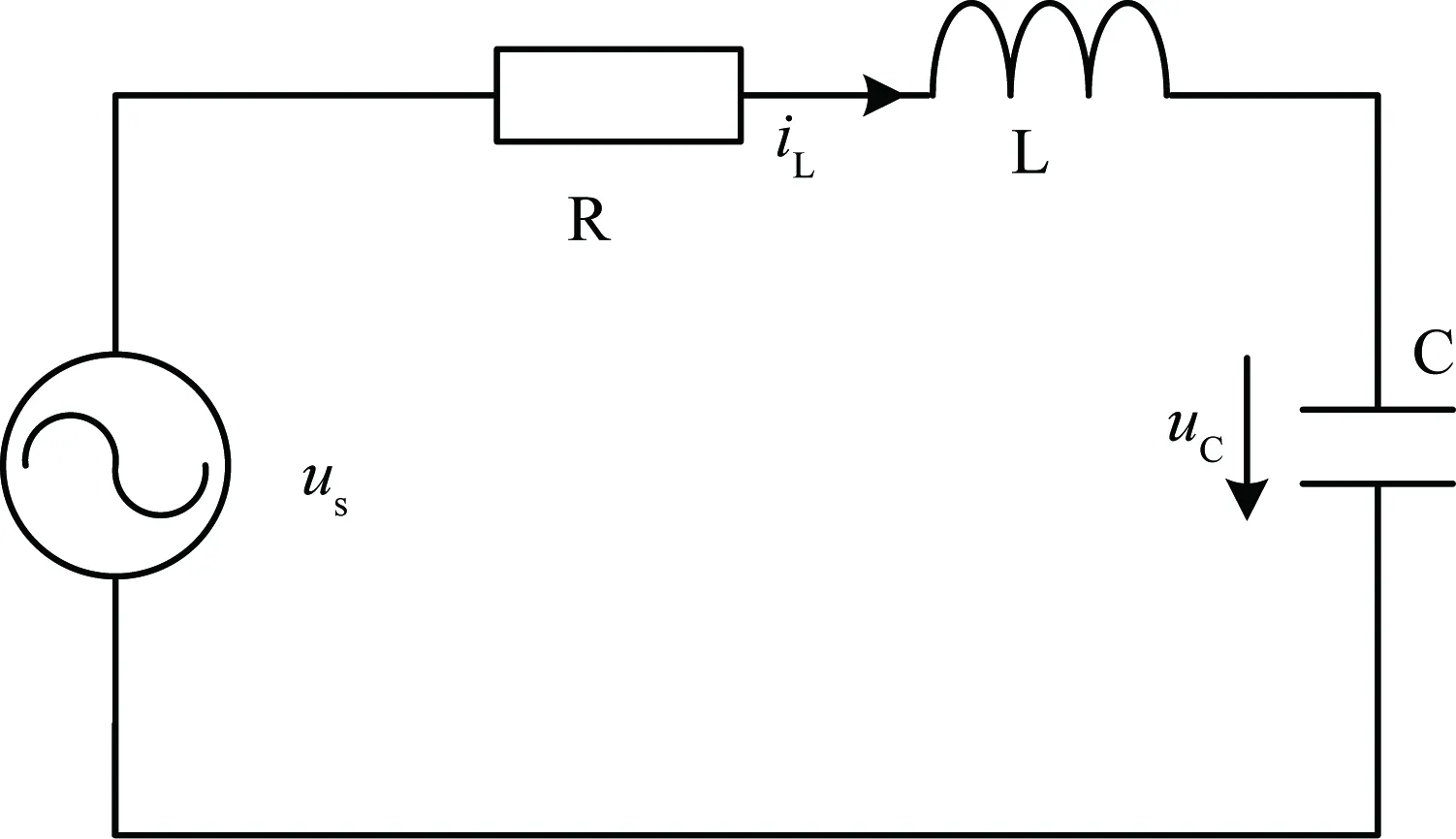
图1 RLC串联电路Fig.1 RLC series circuit

图1所示RLC电路的状态空间方程为

(7)

进而可以求出系统的特征方程为

(8)

若采用s域节点导纳矩阵法，则该电路的s域节点导纳矩阵为：

(9)

而

(10)

显然，在s≠0的条件下，式(8)和式(10)具有相同的零点。这说明采用状态空间法或s域节点导纳矩阵法进行电力网络的谐振稳定性分析，所得结果是完全一致的。

2 基于Y(s)的特征值求解算法

以上分析可知，电力网络特征值求取问题可转化为求解s域节点导纳矩阵行列式等于0的根，即求解如下方程的根：

det[Y(s)]=0

(11)

由于s是复平面上的变量，直接求解上述方程是一件非常困难的事情。现有文献主要采用Newton-Raphson法迭代求解，需要求取Y(s)关于s的导数矩阵[8]。为了能够快速准确地求出det(Y(s))的零点，本文提出实部-虚部交叉迭代的求解方法。

2.1 算法原理

当Y(s)行列式不等于0时，其行列式的倒数为一个有限值；当Y(s)行列式趋近于0时，其行列式的倒数趋向于无穷大。故定义hm(s)为：

(12)

hm(s)在某个特征值附近的示意图如图2所示。需要注意的是，该曲面的顶点在复平面(σ-jω平面)上的投影就是相应的特征值。

当s的实部固定为σi，虚部在一定范围内变化时，如图2所示，相当于平面σ=σi与曲面hm(s)相交的曲线；找出该曲线极大值所对应的虚部坐标，记为jωi。接下来，将s的虚部固定为jωi，而实部在一定范围内变化，如图3所示，相当于平面jω=jωi与曲面hm(s)的交线；找出这条交线的极大值点对应的实部坐标，记为σi+1。

重复上述过程，直到所得的实部和虚部不再改变，或者达到所设定的精度要求为止。最后求出的实部和虚部的组合就是s域下系统的特征值。在电力网络谐振稳定性分析时，系统特征值又称为谐振模式。因此一旦求出系统特征值，则对应此谐振模式的阻尼和频率就是已知的。

图2 平面σ=σi与曲面相交情况Fig.2 Intersection of σ=σi and tapered surface

图3 平面jω=jωi与曲面相交情况Fig.3 Intersection of jω=jωi and tapered surface

2.2 算法流程图

上述的求解思路只是针对1个特征值，对含有多个特征值的系统，其求解过程类似。电力网络特征值的详细求解流程如图4所示。

3 谐振模式的节点电压振型和参与因子矩阵

借鉴文献[11]的做法，可以定义谐振模式sk的节点电压振型和参与因子矩阵。设电力网络的第k个谐振模式为sk，则det[Y(sk)]=0。由矩阵理论知，矩阵行列式的值等于矩阵所有特征值的乘积，因此，复常数矩阵Y(sk)必有一个零特征值=0。设Y(sk)为n阶

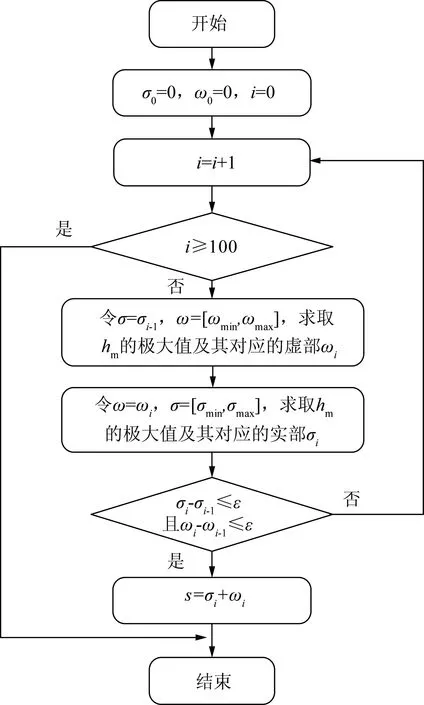
图4 电力网络谐振模式的求解流程图Fig.4 Solving process of electric network resonance modes

Y(sk)=RΛR-1=RΛL

(13)

式中：Λ=diag(λ1,λ2,…,λn)是对角元素为特征值的对角矩阵，不妨设1=0；R=[R1,R2,…,Rn]是Y(sk)的右特征向量矩阵；L=R-1=T是Y(sk)的左特征向量矩阵。且由于Y(sk)为对称矩阵，因此又有R-1=RT。根据s域节点导纳方程式(4)，有

Y(sk)Vnode(sk)=Inode(sk)

(14)

令

Umode=LVnode(sk)

(15)

Jmode=LInode(sk)

(16)

则式(14)可以变换为

(17)

即

(18)

(19)

因此，我们定义R1为对应谐振模式sk的节点电压振型，表示在谐振模式sk下电网中各节点电压的相对大小和相位。而根据式(16)，有

J1=L1Inode(sk)

(20)

因此，根据式(18)～(20)有

(21)

(22)

因此定义矩阵

(23)

为参与因子矩阵，P的元素pij表示在谐振模式sk下电网中节点j的注入电流对节点i电压的相对作用大小。

4 算例及结果分析

4.1 IEEE次同步谐振第一标准测试系统分析

IEEE次同步谐振第一标准测试系统结构如图5所示，发电机参数见文献[12]。发电机的阻抗频率特性采用测试信号法[13]计算得出，如图6所示。

图5 IEEE 次同步振荡第一标准测试系统接线图Fig.5 Single line diagram of IEEE subsynchronousresonance (SSR) first benchmark model

对该测试系统在5～115 Hz频率范围进行固有谐振结构分析，发现存在1个次同步谐振模式，频率fssr=39.3 Hz，衰减因子σssr=-0.454 51/s。由于衰减因子为负，说明该测试系统是谐振不稳定的。该谐振模式的节点电压振型如图7所示，参与因子矩阵如式(24)所示。由节点电压振型图和参与因子列表可见，模式SSR的主要参与节点是3号节点，谐振类型是全局性的。

图6 发电机的阻抗频率特性Fig.6 Impedance-frequency characteristicsof generator

(24)

图7 模式SSR的节点电压振型图Fig.7 Nodal voltage mode shape of mode SSR

4.2 IEEE 39节点测试系统分析

IEEE 39节点测试系统[14]如图8所示。对该测试系统在0～1 500 Hz频率范围进行固有谐振结构分析，结果如表1所示。表1显示该系统在0～1 500 Hz频率范围存在19个谐振模式，所有谐振模式的衰减因子均大于0，说明系统是谐振稳定的。下面对谐振模式1(131.6 Hz)进行详细分析。模式1 (131.6 Hz) 的节点电压振型图如图9所示，数值大于0.1的参与因子矩阵元素只有1个，为p28,28=0.104 1。

由节点电压振型图和参与因子矩阵可见，模式1的主要参与节点是28号和26号、29号节点，谐振类型为局部谐振，主要是28号节点的无功负荷和所连线路的对地电容之间的谐振。

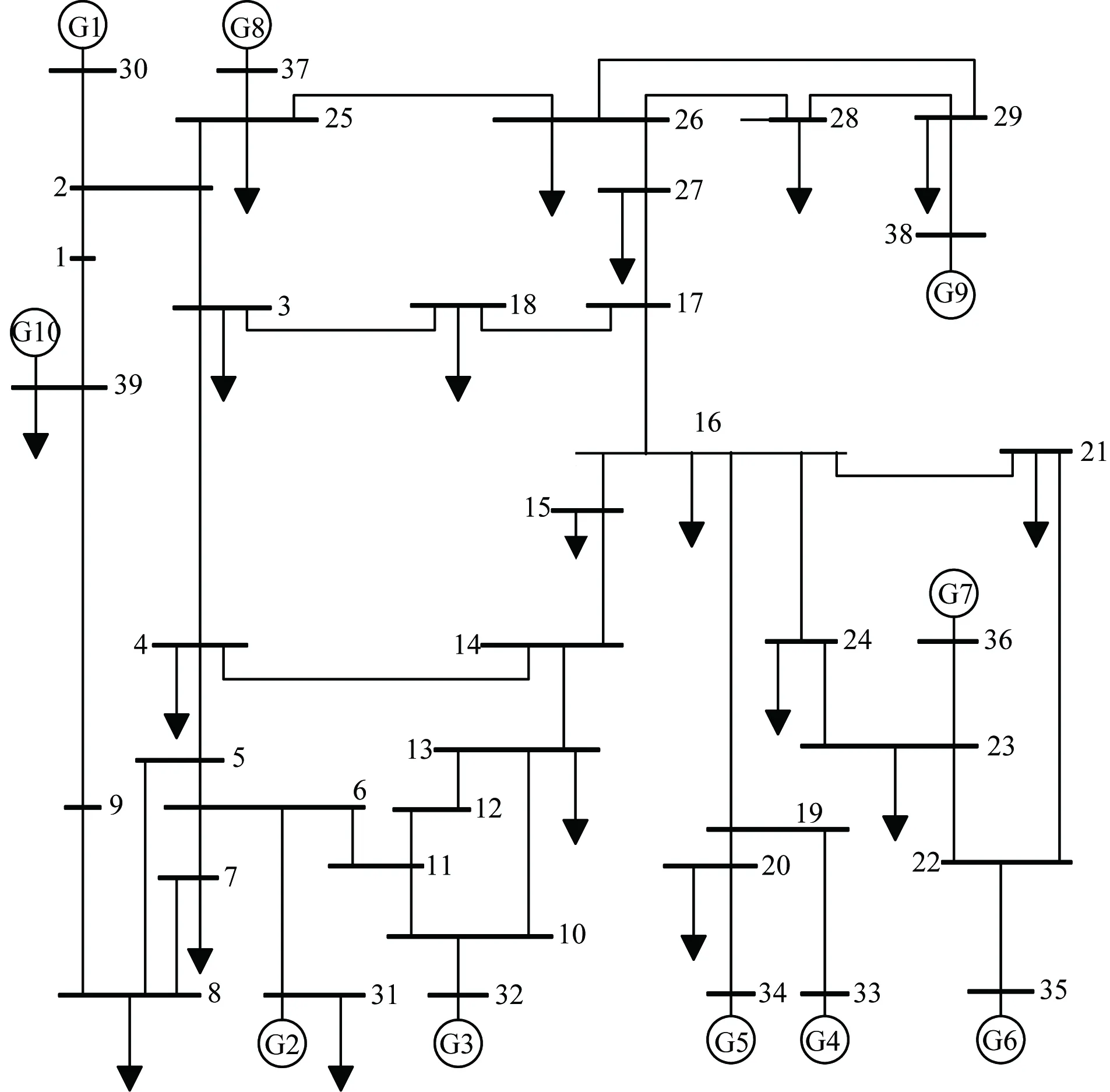
图8 IEEE 39节点测试系统Fig.8 IEEE 39-bus test system

4.3 加入风电场的IEEE 39节点测试系统分析

在IEEE 39节点标准测试系统上增加1个风电场节点，考虑风电场通过远距离输电线路加装50%串补接入到IEEE 39节点标准测试系统的25号节点上，如图10所示。

由双馈风力发电机聚合而成的风电场额定容量 1 500 MW，风机阻抗模型采用文献[15]给出的模型，聚合后风电场在0～100 Hz范围内的阻抗频率特性如图11所示，显示风电场在25～45 Hz频率范围内呈现负电阻-电感特性(相频特性大于90°)。

表1IEEE39节点测试系统的谐振模式
Table1ResonancemodesofIEEE39-bustestsystem

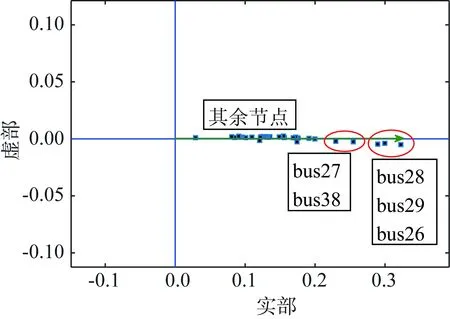
图9 模式1(131.6 Hz)的节点电压振型图Fig.9 Nodal voltage mode shape of mode 1 (131.6 Hz)

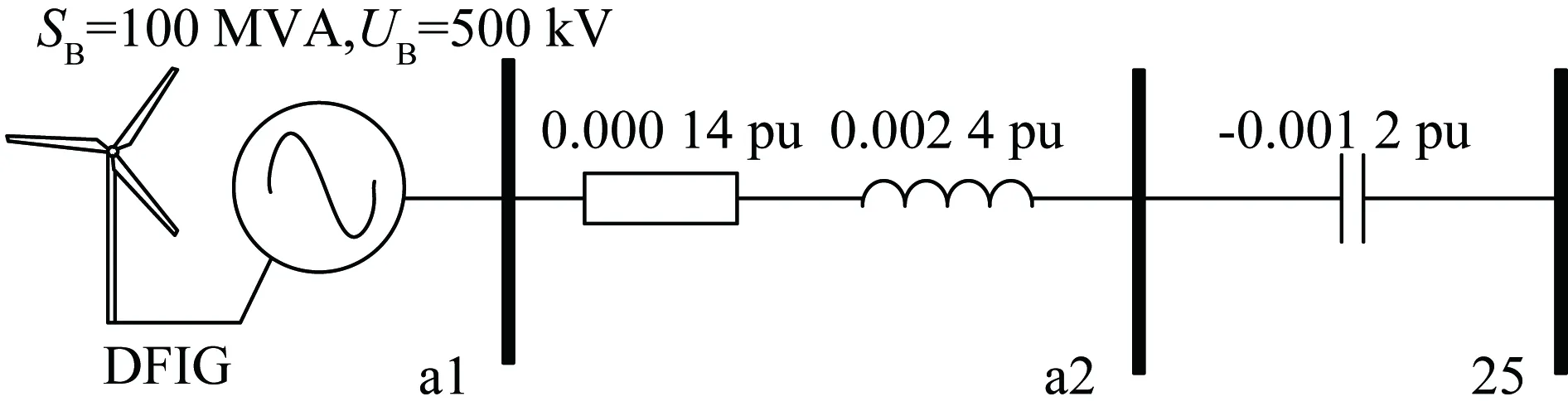
图10 加入到IEEE 39节点标准测试系统上的风电场Fig.10 Wind farm connected to IEEE 39-bus test system

对该系统在0～1 500 Hz频率范围进行固有谐振结构分析，结果如表2所示。表2与表1对比显示，双馈风机通过串补系统接入原系统25号节点后，部分谐振模式发生了变化，如新增了29.8 Hz的谐振模式，而且29.8 Hz的谐振模式衰减因子为负(发散)，说明双馈风机通过串补送出可以引起不稳定的次同步谐振。进一步对不稳定的29.8 Hz谐振模式进行详细分析，得到模式1(29.8 Hz)的节点电压振

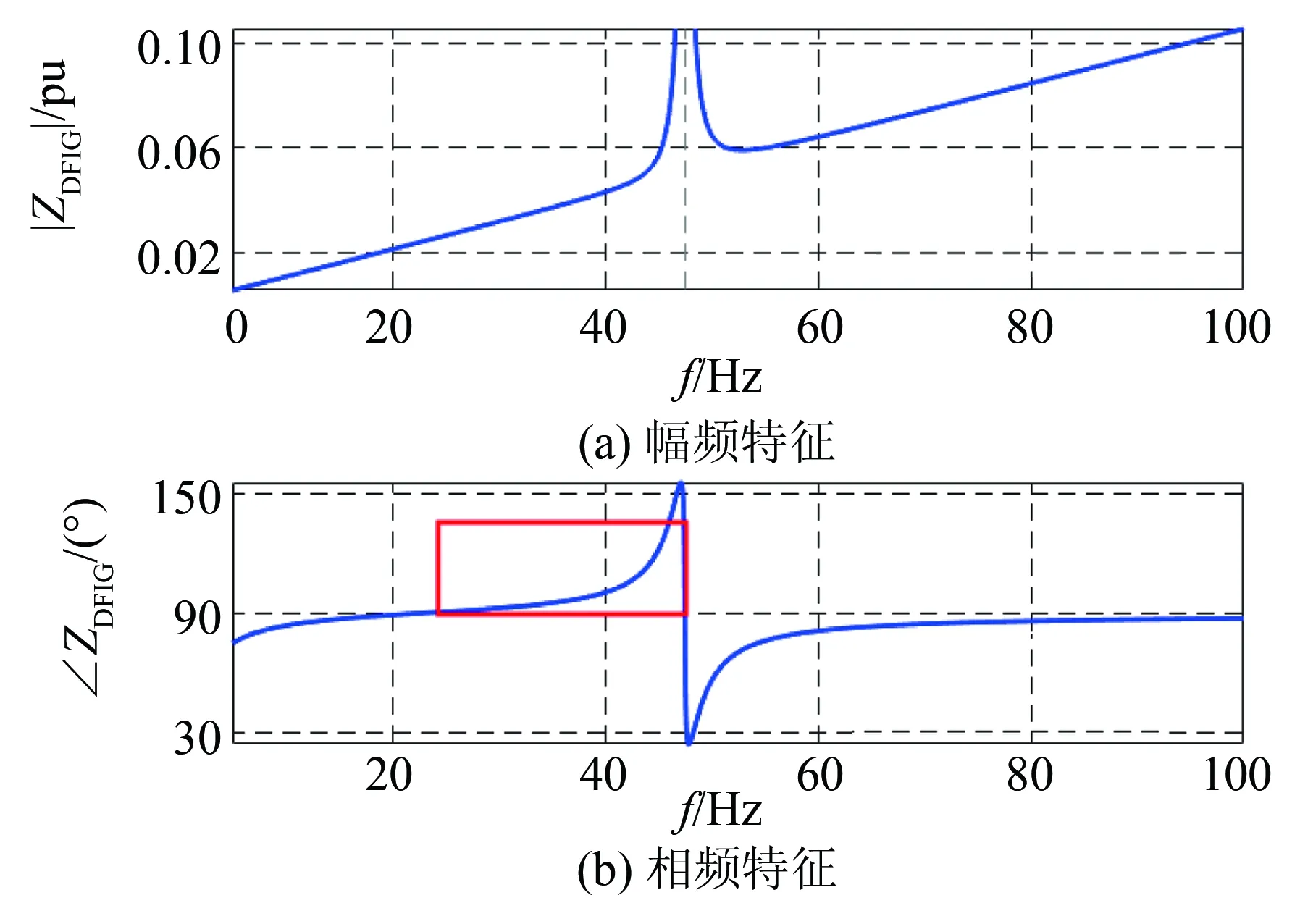
图11 风机阻抗频率特性Fig.10 Impedance-frequency characteristic ofwind generator

图12 模式1(29.8 Hz)的节点电压振型图Fig.12 Nodal voltage mode shape of mode 1 (29.8 Hz)

5 结 论

本文通过构建电力网络的s域节点导纳矩阵，提出了电力网络谐振稳定性的概念，并提出了相应的稳定判据——s域节点导纳矩阵行列式的零点就是系统的特征值，若零点均位于左半平面，则电力网络是稳定的。这一稳定判据对含频变元件和分布参数元件的电力网络具有很好的适用性。在求解零点的过程中，本文提出了一种实部-虚部交叉迭代法，这种求解方法与采用Newton-Raphson迭代求解的方法相比，可以大幅度减少计算量。本文还阐述了在固定谐振模式下电力网络参与因子矩阵和节点电压振型的意义。通过算例分析可以发现：

(1)元件的负电阻效应是导致电力网络谐振不稳定的主要原因，同步发电机在次同步低频段(低于基频)由于异步发电机效应会表现出负电阻；

(2)双馈风机在次同步频段也存在着负电阻效应，它的接入可能会引起电力网络在次同步频段的谐振不稳定；

(3)电力网络的谐振模式通常表现为2种形式：一种是节点对地的谐振模式，主要特征为节点电压的振型接近于同一方向；另一种是节点对节点的谐振模式，主要特征为节点电压的振型会存在2个明显相反的方向。

[1] Kundur Prabha, Balu Neal J, Lauby Mark G. Power system stability and control[M]. McGraw-hill New York, 1994.

[2] 徐政. 交直流电力系统动态行为分析[M]. 北京: 机械工业出版社, 2005.

[3] 吕敬, 董鹏, 施刚，等. 大型双馈风电场经MMC-HVDC并网的次同步振荡及其抑制[J]. 中国电机工程学报, 2015, 35(19): 4852-4860.

LÜ Jing, DONG Peng, SHI Gang,et al. Subsynchronous Oscillation and Its Mitigation of MMC-Based HVDC With Large Doubly-Fed Induction Generator-Based Wind Farm Integration[J]. Proceedings of the CSEE, 2015, 35(19): 4852-4860.

[4] 李云丰, 汤广福, 贺之渊，等. MMC型直流输电系统阻尼控制策略研究[J]. 中国电机工程学报, 2016,36(20): 5492-5503.

LI Yunfeng, TANG Guangfu, HE Zhiyuan,et al. Damping Control Strategy Research for MMC Based HVDC System[J]. Proceedings of the CSEE, 2016, 36(20): 5492-5503.

[5] 李明节, 于钊, 许涛，等. 新能源并网系统引发的复杂振荡问题及其对策研究[J]. 电网技术, 2017, 41(4): 1035-1042.

LI Mingjie, YU Zhao, XU Tao,et al. Study of Complex Oscillation Caused by Renewable Energy Integration and Its Solution[J]. Power System Technology, 2017, 41(4): 1035-1042.

[6] 王锡凡, 方万良, 杜正春. 现代电力系统分析[M]. 北京：科学出版社, 2003.

[7] Semlyen A I. s-domain methodology for assessing the small signal stability of complex systems in nonsinusoidal steady state[J]. IEEE Transactions on Power Systems, 1999, 14(1): 132-137.

[8] Gomes S, Martins N, Portela C. Modal analysis applied to s-domain models of AC networks[C]//IEEE Power and Energy Society.Proceedings of 2001 IEEE Power Engineering Society Winter Meeting,2001.1.28—2001.2.1, Columbus, Ohio, USA: 1305-1310.

[9] Lima L T G, Martins N, Carneiro S. Augmented state-space formulation for the study of electric networks including distributed-parameter transmission line models [C]// IPST commission.Proceedings of 1999 International conference on power systems transients,1999.6.20-24, Budapest, Hungary:87-92.

[10] Varricchio S L, Martins N, Lima L T G. A Newton-Raphson method based on eigenvalue sensitivities to improve harmonic voltage performance[J]. IEEE Transactions on Power Delivery, 2003, 18(1): 334-342.

[11] Xu W, Huang Z, Cui Y, et al. Harmonic resonance mode analysis[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1182-1190.

[12] IEEE subsynchronous resonance task force. First benchmark model for computer simulation of subsynchronous resonance[J]. IEEE Trans on Power Apparatus and Systems, 1977,96(5):1565-1572.

[13] Xu Zheng, Feng Zhouyan. A novel unified approach for analyzing small-signal stability of power systems[C]//IEEE Power and Energy Society.Proceedings of 2000 IEEE Power Engineering Society Winter Meeting,2000.1.23-27, Singapore:963-967.

[14] Ramos R A, Hiskens I, Canizares C, et al. Benchmark systems for small-signal stability analysis and control[R]. IEEE Power and Energy Society Technical Report PES-TR18, 2015.

[15] Miao Z. Impedance-Model-Based SSR Analysis for Type 3 Wind Generator and Series-Compensated Network[J]. IEEE Transactions on Energy Conversion, 2012, 27(4): 984-991.

2017-09-10

徐政(1962)，男，博士，教授，通信作者，主要研究方向：大规模交直流电力系统分析、直流输电与柔性交流输电、风力发电技术与风电场并网技术；

王世佳(1991)，男，博士研究生，主要研究方向：交直流电力系统次同步振荡；

邢法财(1993)，男，博士研究生，主要研究方向：新能源并网的交直流系统稳定性研究；

肖晃庆(1990)，男，博士研究生，主要研究方向：直流输电与柔性交流输电。

(编辑 魏希辉)

QualitativeAnalysisMethodofElectricNetworkResonanceStability

XU Zheng, WANG Shijia, XING Facai, XIAO Huangqing

(College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China)

With the increasing utilization of power electronic equipment in power systems, in recent years,a number of new oscillations with unknown mechanisms have emerged. This paper puts forward the concept of the electric network resonance stability, and tries to classify the unclear reason oscillations mentioned above into the electric network resonance instability category. Thus, many complex power system oscillations can be analyzed by the linear network theory, which provides an approach to solve the actual power system problems by the mathematically mature linear system theory. The objective of this paper is to establish a method for analyzing the electric network resonance stability. By introducing the s-domain nodal admittance matrix of the electric network, this paper transforms the discrimination of the electric network resonance stability into the distribution problem in complex plane of zero point of the determinant of the s-domain nodal admittance matrix. Firstly, it is proved that the zero points of the determinant of the s-domain nodal admittance matrix are actually the eigenvalues of the system. Secondly, we use the cross iteration method of the real part and the imaginary part of the zero point to solve the zero points of the determinant of the s-domain nodal admittance matrix. Thirdly, we derive the nodal voltage mode shape and the participation factor matrix corresponding to a particular resonance mode, which can be used to locate the resonant region of this particular resonance mode in the network. Finally, we illustrate the effectiveness of the proposed method for analyzing the resonance stability of electric networks by several studied cases.

electric network; state space model; s-domain nodal admittance matrix; resonance mode; resonance stability;nodal voltage mode shape; participation factor matrix

国家高技术研究发展计划项目(863计划)(2011AA05A119)；国家电网公司科技项目(柔性输电网规划评估方法及应用关键技术研究)

Project supported by The National High Technology Research and Development of China (863 Program)( 2011AA05A119)

TM711

A

1000-7229(2017)11-0001-08

10.3969/j.issn.1000-7229.2017.11.001