对一道导数取值范围问题的探索

■甘肃省陇南市礼县职业中等专业学校 杨 虎

对一道导数取值范围问题的探索

■甘肃省陇南市礼县职业中等专业学校 杨 虎

编者的话:“经典题突破方法”栏目里例、习题选名校模拟题或三年高考真题,推出本栏目的主要目的是让同学们更好地领悟数学解题思想方法,通过多解多变培养同学们多思多想的好习惯。学会解题反思,无疑是同学们学习的一条捷径,愿同学们不断在反思中进步,在反思中收获!

一、题目呈现及思路分析

(Ⅰ)若函数y=f(x)存在极大值和极小值,求a的取值范围;

(Ⅱ)设m,n分别为f(x)的极大值和极小值,其中m=f(x1),n=f(x2),且x1∈,求m+n的取值范围。分析:(Ⅰ)因为函数f(x)=a x2-2x+al nx(a∈R),所以要求函数y=f(x)的极大值和极小值,就要对函数进行求导,保证导函数对应的方程有两个不相等的正实根,通过判别式大于零和根与系数的关系即可得到结论。(Ⅱ)根据极大值与极小值的含义得到两个相应的方程,由两个极值点的关系可以将其中一个消去,进一步可得关于极大值点的代数式,再通过基本不等式与导数求m+n的取值范围。

二、多解探索

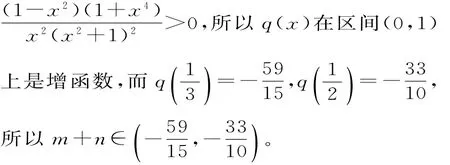
点评:本题考查了利用导数、基本不等式求极值及参数的范围问题,在这类问题的解决中要善于把握函数与不等式的关系,导数为零与函数极值的关系,正确运用消元法解方程,以及对参数进行适当的分类讨论,在本题中合理利用消元思想与基本不等式,以及利用导数求参数的取值范围是顺利求解的前提和关键。

三、变式探索

例2 (2 0 1 7年山西三区八校理科模拟试题)已知函数f x()=l nx+a x2+b x(其中a,b为常数且a≠0)在x=1处取得极值。

(Ⅰ)当a=1时,求f x()的单调区间;

(Ⅱ)若f x()在 0,e( ]上的最大值为1,求a的值。

点评:可以说极值是一个与导数紧密相连的概念,只要提到极值或极值点就会想到导数,本变式的关键是要注意极值与最值的区别,极值是一个局部的概念,而最值是一个整体的概念,在对函数求导得出极值后,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于参数的方程求得结果。

例3 (2 0 1 7年马鞍山理科二模试题)已知函数f (x)=l nx+

(Ⅰ)证明曲线f x()上任意一点处切线的斜率不小于2;

(Ⅱ)设k∈R,若g x()=f x()-2k x有两个极值点x1,x2,且x1＜x2,证明:g x2()＜-2。

点评:本题考查了利用导数研究函数的单调性,亮点是把导数与不等式的证明结合,要想准确解答,首先要观察不等式的特点,结合韦达定理进行化简变形,进一步利用导数及函数的单调性证明结论。

解后感悟:本题是一道考查导数在研究函数性质中的应用的好题,其中渗透着分类讨论、数形结合、转化与化归等思想方法,重在考查同学们结合所学知识分析问题、解决问题的能力。

(责任编辑 王福华)