集合、函数、导数核心考点B卷

■郑州市第十一中学 李小斌

集合、函数、导数核心考点B卷

■郑州市第十一中学 李小斌

编者的话:强化对核心考点的演练、注重对经典题型的归纳,是学好数学的秘诀,基于此,本刊编辑部特开设此栏目,希望同学们能认真对待。从本期开始,如果都能把试卷保存好,对以后的复习大有裨益。

一、选择题

1.已知集合A={x|y=l o g2(x-1)},B={x|x＜2m-1},且A⊆∁RB,那么m的最大值是( )。

A.[-3,0) B.{-3,-2,-1}

C.{-3,-2,-1,0}

D.{-3,-2,-1,1}

3.若集合N至少含有两个元素(实数),且N中任意两个元素之差的绝对值都大于2,则称 N 为 “好集合”,已知集合 M=,则M的子集中共有( )个好集合。

A.7 5 B.7 6 C.4 8 D.4 9

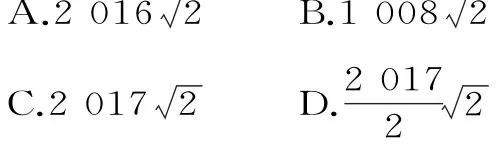
5.设函数f:N*→N*且严格递增,当m、n互质时,f(m·n)=f(m)·f(n),若f(3 2)=3 2,则f(3 2)·f(f(6 3))=( )。

A.20 1 6 B.20 1 7

C.20 1 5 D.20 1 4

A.可导 B.不一定可导

C.一定不可导 D.不一定连续7.函数y=x+2 7+1 3-x+x的最小值为( )。

A.3 3+1 3 B.2 3+1 3

C.1 1 D.1 0

An.π+2n2Bn.π+n2

C.2n2π+n Dn.2π+2n

1 1.若函数y=x2-3x-4的定义域为[0,m],值域为,则m的取值范围是( )。

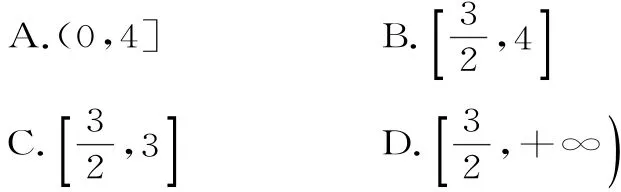
1 2.函数y=esinx(-π≤x≤π)的大致图像为图1中的( )。

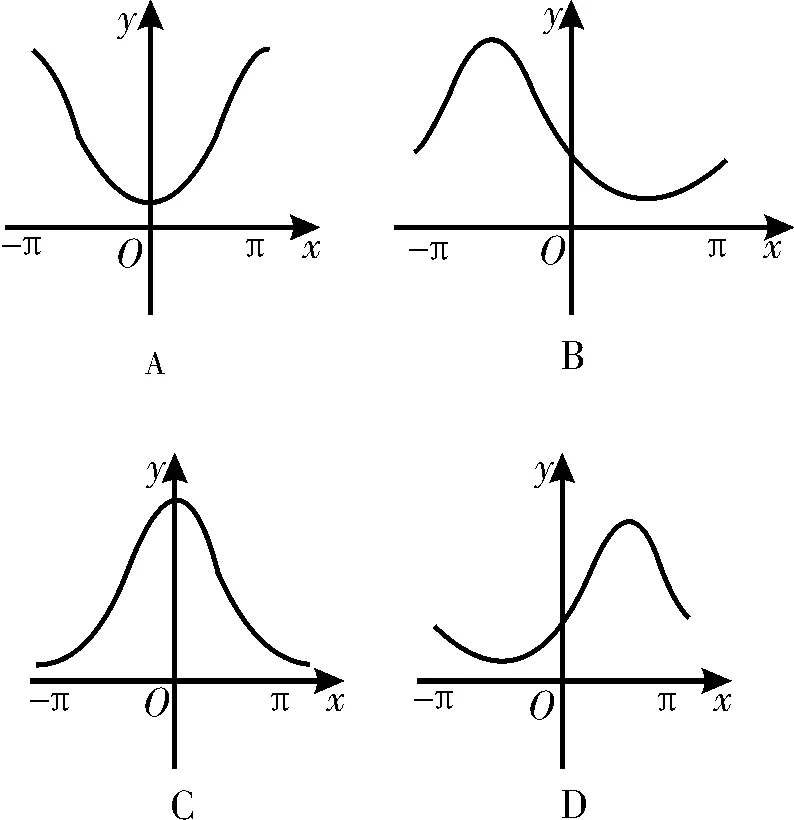
图1

1 3.x为实数,[x]表示不超过x的最大整数,则函数f(x)=x-[x]在 R上为( )。

A.奇函数 B.偶函数

C.增函数 D.周期函数

A.0 B.1 C.2 D.4

1 5.如果把太极图中的“S形线”称作“和谐线”,那么,能够把圆O:x2+y2=1 6的周长和面积同时分为相等的两部分的函数称作圆O的“和谐函数”。下列函数不是圆O的“和谐函数”的是( )。

2 1.已知f(x)=x(20 1 7+l nx),f'(x0)=20 1 8,则x0等于( )。

A.e2B.1 Cl. n2 D.e

2 2.曲线y=al nx(a＞0)在x=1处的切线与两坐标轴所围成的三角形的面积为4,则a的值为( )。

A.4 B.-4 C.8 D.-8

2 3.若函数f(x)=x2+a x+在上是增函数,则a的取值范围是( )。

A.[-1,0] B.[-1,+∞)

C.[0,3] D.[3,+∞)

2 4.一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度v(t)=7―3t+(t的单位:s,v的单位:m/s)行驶至停止。在此期间汽车继续行驶的距离(单位:m)是( )。

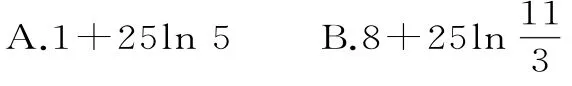
C.4+2 5 l n5 D.4+5 0 l n2

2 5.如图2所示,在边长为1的正方形O A B C中任取一点P,则点P恰好取自阴影部分的概率为( )。

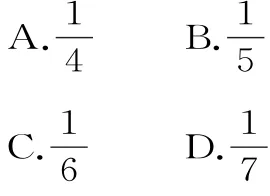
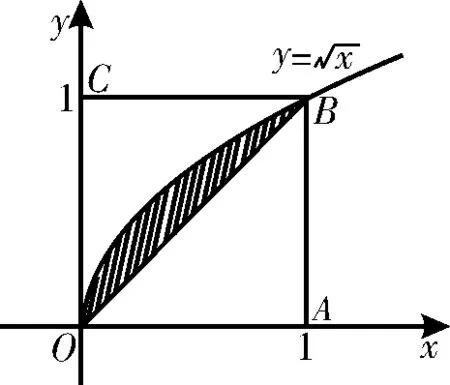
图2

2 6.由曲线y=x,直线y=x-2及y轴所围成的图形的面积为( )。

2 7.设函数f(x)=ex+x-2,g(x)=l nx+x2-3。若实数a,b满足f(a)=0,g(b)=0,则( )。

A.g(a)＜0＜f(b)

B.f(b)＜0＜g(a)

C.0＜g(a)＜f(b)

D.f(b)＜g(a)＜0

2 8.已知函数y=f(x)是定义在R上的偶函数,且当x＞0时,不等式f(x)+x·f'(x)＜0成立,若a=30.2·f(30.2),b=(l o gπ2)·f(l o gπ2),c=则a,b,c间的大小关系为( )。

Ac.＞b＞a Bc.＞a＞b

Cb.＞a＞c Da.＞c＞b

二、填空题

2 9.设集合A={x|x2+2x-3＞0},集合B={x|x2-2a x-1≤0,a＞0}。若A∩B中恰含有一个整数,则实数a的取值范围是____。

3 0.若集合{a,b,c,d}={1,2,3,4}且下列四个关系:①a=1;②b≠1;③c=2;④d≠4有且只有一个是正确的,则符合条件的有序数组(a,b,c,d)的个数是___________。

-m。若∀x1∈[1,2],∃x2∈[-1,1],使f(x1)≥g(x2),则实数m的取值范围是____。

4 2.在平面直角坐标系x O y中,已知点P是函数f(x)=ex(x＞0)的图像上的动点,该图像在点P处的切线l交y轴于点M,过点P作l的垂线交y轴于点N,设线段MN的中点的纵坐标为t,则t的最大值是____。

三、解答题

(1)求实数a的值。

4 3.设二次函数f(x)=a x2+b x+c(a≠0)在区间[-2,2]上的最大值、最小值分别是M、m,集合A={x|f(x)=x}。

(1)若A={1,2},且f(0)=2,求M和m的值。

(2)若A={1},且a≥1,记g(a)=M+m,求g(a)的最小值。

4 4.对正整数n,记In={1,2,3,…,n},

(1)求集合P7中元素的个数。

(2)若Pn的子集A中任意两个元素之和不是整数的平方,则称A为“稀疏集”。求n的最大值,使Pn能分成两个不相交的稀疏集的并。

(1)求f(1)的值。

(2)证明:f(x)为单调递减函数。

(3)若f(3)=-1,求f(x)在[2,9]上的最小值。

4 6.已知函数f(x)在R上满足f(2-x)=f(2+x),f(7-x)=f(7+x),且在闭区间[0,7]上,只有f(1)=f(3)=0。

(1)试判断函数y=f(x)的奇偶性。

(2)试求方程f(x)=0在闭区间[-20 1 4,20 1 4]上根的个数,并证明你的结论。

(2)记集合E={y|y=f(x),x∈{-1,1,2}},λ=l g22+l g2·l g5+l g5-,判断

λ与E的关系。

(1)求f(x)的解析式。

间(0,2]上为减函数,求实数a的取值范围。

4 9.省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数f(x)与时刻x(时)的关系为f,x∈[0,2 4],其中a是与气象有关的参数,且a∈[0,1],若用每天f(x)的最大值作为当天的综合放射性污染指数,并记作M(a)。

(2)省政府规定,每天的综合放射性污染指数不得超过2,试问:目前市中心的综合放射性污染指数是否超标?

(1)求函数f(x)的单调区间。

(2)试问:过点(2,5)可以作多少条直线与曲线y=g(x)相切?请说明理由。

5 1.已知函数f(x)=x2+a x+b,g(x)=ex(c x+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2。

(1)求a,b,c,d的值;

(2)若x≥-2时,f(x)≤k g(x),求k的取值范围。

(责任编辑 刘钟华)