集合、函数、导数核心考点A卷

■郑州市第七中学 王三兴(高级教师)

集合、函数、导数核心考点A卷

■郑州市第七中学 王三兴(高级教师)

A.1 B.2 C.-1 D.-2

8.设集合S={1,2,3,…,5 1}的子集具有性质“S中任意两个不同元素之和不被7整除”,则S中元素个数的最大值为( )。

编者的话:强化对核心考点的演练、注重对经典题型的归纳,是学好数学的秘诀,基于此,本刊编辑部特开设此栏目,希望同学们能认真对待。从本期开始,如果都能把试卷保存好,对以后的复习大有裨益。

一、选择题

1.已 知 集 合 A={x |x2＞1},B={-2,-1,0,2},则A∩B=( )。

A.{0,-1} B.{-2,-1}

C.{-2,2} D.{0,2}

Ab.＜a＜c Bc.＜a＜b

Cc.＜b＜a Db.＜c＜a

3.已知集合A={x|-3＜x＜1},B={x|x2-2x≤0},则A∪B=( )。

A.{x|0＜x＜1}

B.{x|0≤x＜1}

C.{x|-3＜x＜2}

D.{x|-3＜x≤2}

4.已知函数f(x)的定义域为[0,2],则函数g(x)=f(2x)+8-2x的定义域为( )。

A.[0,1] B.[0,2]

C.[1,2] D.[1,3]

5.曲线y=3 l nx+x+2在点P0处的切线方程为4x-y-1=0,则点P0的坐标是( )。

A.(0,1) B.(1,0)

C.(1,-1) D.(1,3)

6.设集合M={x||x|＜1},N={y|y=2x,x∈M},则集合∁R(M∩N)等于( )。

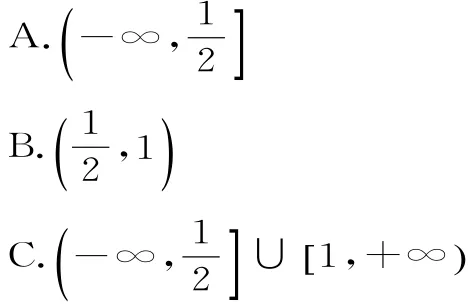
A.2 4 B.2 3 C.2 2 D.2 1

9.已知命题p:方程x2+m x+2=0有两个不等的负实根;命题q:方程4x2+4(m-2)x-1=0无实根。若p或q为真,p且q为假,则实数m的取值范围为( )。

A.(-1,2 2)∪[5,+∞)

B.(-1,2 2]∪[5,+∞)

C.(-1,2)∪[5,+∞)

D.(-1,2]∪[5,+∞)

1 0.设不等式x2-2a x+a+2≤0的解集为S,若S⊆[1,4],则实数a的取值范围是( )。

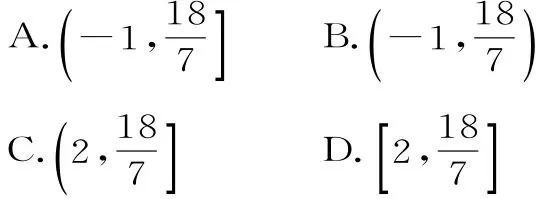
1 1.在一个以A B为弦的弓形中,C为圆弧A B的中点,自A,B分别作圆弧A B的切线,交于D点,设x为弦A B所对的圆心角,则

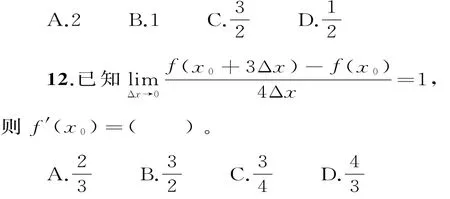
A.2 B.-1 C.1 D.0

1 4.已知函数f(x)=a x4+b x3+c x2+d x+e为偶函数,其图像过点A(0,-1),且在x=1处的切线方程为y=-2x+2,则y=f(x)的表达式为( )。

A.-2x4+3x2-1

B.-3x4+3x2-1

C.-3x4+4x2-1

D.-4x4+3x2-1

A.1 B.-1 C.±1 D.0

1 7.下列四类函数中,具有性质“对任意的x＞0,y＞0,函数f(x)满足f(x y)=f(x)+f(y)”的是( )。

A.幂函数 B.对数函数

C.指数函数 D.一次函数

1 9.函数f(x)=x3+a x2+(a+6)x+1有极大值和极小值,则实数a的取值范围是( )。

A.(-1,2) B.(-3,6)

C.(-∞,-3)∪(6,+∞)

D.(-∞,-1)∪(2,+∞)

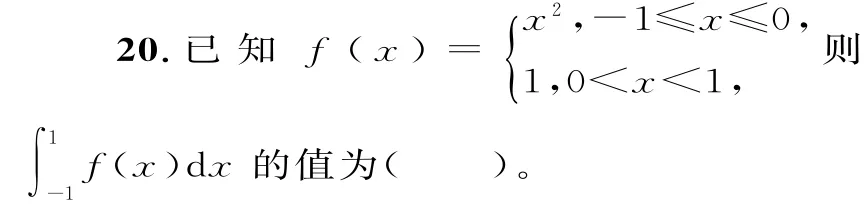
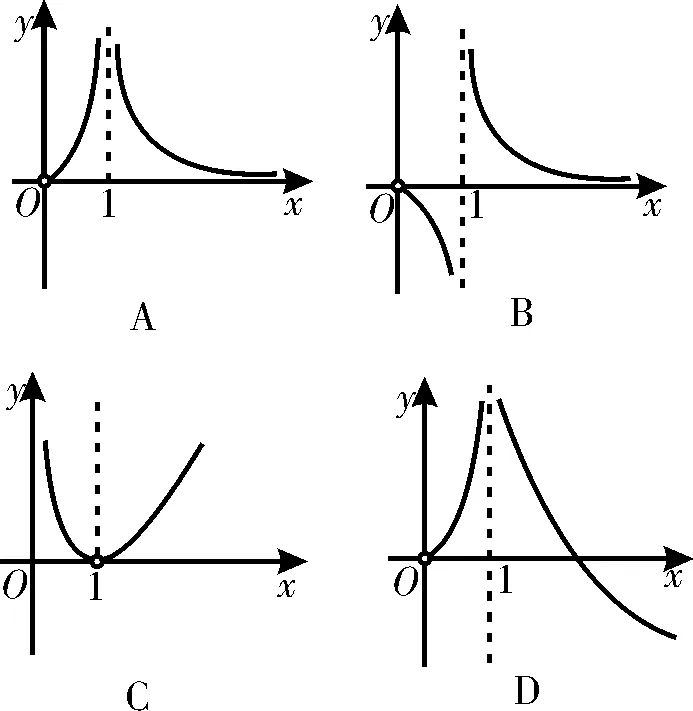
图1

A.[-1,1) B.[-1,2)

C.[-2,2) D.[0,2]

2 3.已知M={(x,y)|x2+2y2=3},N={(x,y)|y=m x+b}。若对于所有的m∈R,均有M∩N≠∅,则b的取值范围是( )。

A.2+|x+1| B.3-|x+1|

C.|x-2| D.|x+4|

A.(-∞,-1) B.(-1,0)

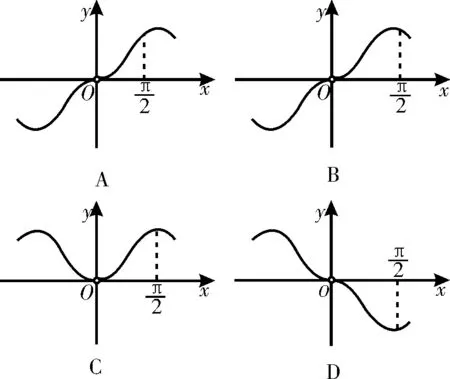
图2

2 7.已知函数f(x)是定义在R上的奇函数,f(1)=0,当 x ＞0 时,有成立,则不等式x·f(x)＞0的解集是( )。

A.(-∞,-1)∪(1,+∞)

B.(-1,0)∪(0,1)

C.(1,+∞)

D.(-1,0)∪(1,+∞)

2 8.已知定义在R上的函数y=f(x)满足条件f(x+4)=-f(x),且函数y=f(x+2)是偶函数,当x∈(0,2]时,f(x)=l nx-a x,当x∈[-2,0)时,f(x)的最小值为3,则a的值等于( )。

A.e2B.e C.2 D.1

2 9.已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,记a=f(l o g0.53),b=f(l o g25),c=f(2m),则a,b,c的大小关系为( )。

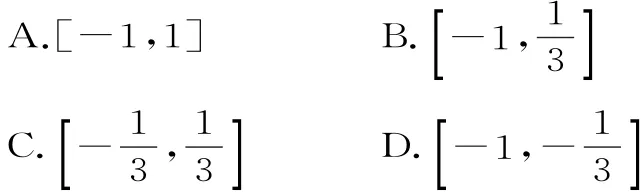
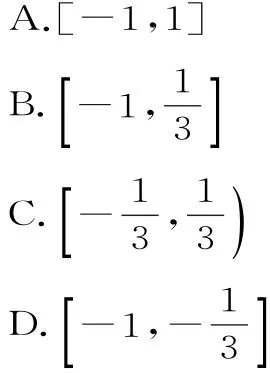
3 1.若函数f(x)=k x-l nx在区间(1,+∞)上单调递增,则k的取值范围是( )。

A.(-∞,-2]

B.(-∞,-1]

C.[2,+∞)

D.[1,+∞)

3 2.如图3,长方形的边A B=2,B C=1,O是A B的中点,点P沿着边B C、C D与DA运动,记∠B O P=x,将动点P到A,B两点距离之和表示为x的函数f(x),则f(x)的图像大致为图4中的( )。

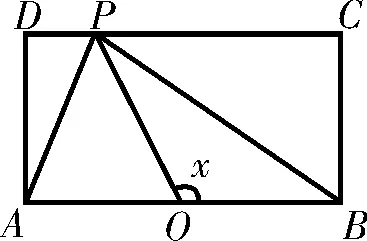
图3

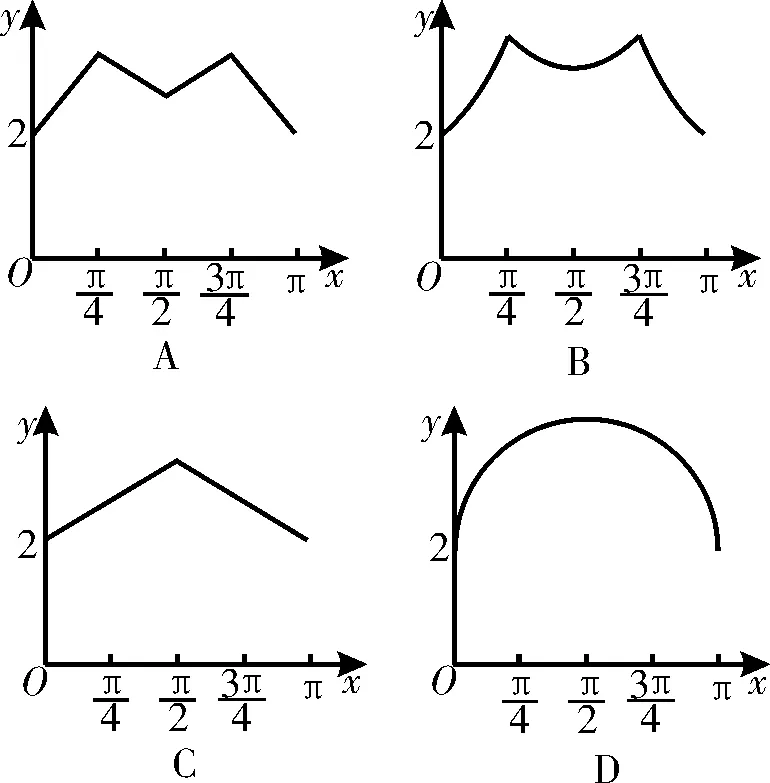
图4

4 3.设函数y=f(x)的定义域为D,如果存在非实数T对任意的x∈D都有f(x+T)=T f(x),则称函数y=f(x)是“似周期函数”,非零常数T为函数y=f(x)的似周期。现有下列四个关于“似周期函数”的命题:

①如果“似周期函数”y=f(x)的“似周期”为-1,那么它是周期为2的周期函数;

②函数f(x)=x是“似周期函数”;

③函数f(x)=2-x是“似周期函数”;

④如果函数f(x)=c o sω x是“似周期函数”,那么ω=kπ,k∈Z。

其中为真命题的序号是____。(请填写所有满足条件的命题序号)

三、解答题

4 4.若二次函数满足f(x+1)-f(x)=2x+3,且f(0)=2。

(1)求f(x)的解析式;

(2)若在区间[-1,1]上不等式f(x)＞-2x+m恒成立,求实数m的取值范围。

4 5.已知f(l o g2x)=a x2-2x+1-a,a∈R。

(1)求f(x)的解析式;

(2)求f(x)的值域;

4 6.已知函数f(x)=a x3+x2(a∈R)在x=-处取得极值。

(1)确定a的值;

(2)若g(x)=f(x)ex,讨论函数g(x)的单调性。

4 7.定义在R上的单调函数f(x)满足f(2)=l n且对任意x,y∈R都有f(x+y)=f(x)+f(y)。

(1)求证:f(x)为奇函数。

(2)若f(k·4x)+f(3x+2x+1)＜0对任意x∈(-∞,1]恒成立,求实数k的取值范围。

4 8.已知函数f(x)=ex-a x2-2a x-1。

(1)当a=1时,求曲线y=f(x)在点(-1,f(-1))处的切线方程;

(2)当x＞0时,f(x)＞0恒成立,求实数a的取值范围。

4 9.已知函数f(x)=x2-(a-2)xal nx(a∈R)。

(1)求函数y=f(x)的单调区间;

(2)当a=1时,证明:对任意的x＞0,f(x)+ex＞x2+x+2。

(责任编辑 刘钟华)