轻质旋转体在水平匀速转动圆盘上的多种运动模式

穆翔栩 关国业 张博文 林 方

(四川大学物理科学与技术学院,成都610064)

轻质旋转体在水平匀速转动圆盘上的多种运动模式

穆翔栩1)关国业 张博文 林 方2)

(四川大学物理科学与技术学院,成都610064)

将一个轻质旋转体(如球、圆环、圆盘等)释放于水平匀速转动的圆盘上，旋转体可能存在多种不同类型的运动轨迹，探究了其中4种运动模式.在纯滚动假设前提下，建立了旋转体动力学方程并数值求解，分别得出不同模式下旋转体的运动轨迹及轨迹特征参数，并进行了定量实验对比.还提出并通过实验验证了一个发现，即不论旋转体处于何种运动模式，其质心运动的相位角周期都将收敛于一个由旋转体形状、大小和质量分布决定的极限值.

旋转体,转动圆盘,滚动摩擦,质心相位角

轻质旋转体(如球、圆环、圆盘等)在匀速定轴转动圆盘上的运动存在多种不同类型的轨迹，该类问题在20世纪70年代末开始被深入研究.1979年，Weltner[1]首先研究了不考虑滚动摩擦的情况，得到了旋转体做匀速圆周运动时运动周期与转盘转动周期成正比的结论.1981年，Burns[2]将匀速转盘上球体的运动与带电粒子在磁场中的运动进行了类比.1985年，Voyenli等[3]研究了冰球在转盘上纯滚动与纯滑动这两种运动状态.1987年，Weltner[4]以旋转圆锥面代替水平转盘，探究了球体在锥面上的运动模式，通过实验发现和证明了球体出现向圆心靠近的螺旋运动模式是滚动摩擦作用的结果，据此设计了一种测量滚动摩擦系数的新方法.1992年，Gersten等[5]针对球体提出了一种滚动摩擦作用的新原理并应用于转盘上球体运动问题的分析中.1994年，Sokirko等[6]进一步针对环状物在匀速转盘上的运动进行了理论推导与数值模拟，得到了不同初始条件下环状物的不同运动模式.1995年，Ehrlich等[7]对匀速转盘上的球体运动进行了数值模拟.1996年，Soodak等[8]从滚动摩擦入手，对该力学系统进行了摄动分析.1997年，Weckesser[9]从能量角度推导得到了球体做匀速圆周运动时的理论轨迹.此后，在2011年，M´unera[10]对匀速转盘上球体的部分运动模式相图进行了数值模拟.2015年，Agha等[11]研究了球体运动始终不离开匀速转盘的初值限制范围.

轻质旋转体在匀速旋转圆盘上存在多种运动模式，通过研究其运动特性，可以设计出精确测量滚动摩擦系数、滑动摩擦系数和转动惯量等物理量的新方法.因此，该问题在工程应用上具有研究价值.匀速转动圆盘上的旋转体运动问题亦出现在2016年第29届国际青年物理学家锦标赛 (29th International Young Physicists’Tournament)上.图1展现了乒乓球在水平转动圆盘上的两种运动模式：圆周运动和螺旋向外运动.

本文主要内容包括：(1)通过纯滚动假设，建立了描述旋转体运动的动力学方程，借助数学软件Mathematica求解得到了旋转体可能存在的4种运动类型;(2)设计实验，采用物体追踪软件Tracker记录旋转体的运动轨迹，并将之与相同参数、相同初始条件下理论计算得到的运动轨迹做对比;(3)本文还发现一个新现象，匀速转动圆盘上的旋转体无论做何种运动，其质心运动的相位角周期都必将收敛于极限值2π/γωD，其中ωD为转盘角速度，无量纲常数γ则取决于旋转体的转动惯量I、质量m和最大半径R.

图1 乒乓球在水平转动的铝制圆盘上滚动

1 理论分析

以水平转盘的圆心为坐标原点O，竖直向上方向为 z轴，建立柱坐标系 (r,θ,z)，如图 2所示.其中，3个方向的单位矢量分别为er,eθ和ez.假设旋转体(球体、圆盘、圆环等)在初始时刻滚动角速度 ω0指向原点 O，且旋转体在转盘上进行的运动始终为纯滚动(无滑滚动)，即满足关系

其中，ω0和r0分别为初始时刻旋转体滚动角速度与质心位矢；ωD为转盘转动角速度，ω为旋转体相对质心的滚动角速度；r为旋转体质心位矢；v为旋转体质心速度，R 为旋转体的半径矢量，方向从质心指向旋转体与转盘的接触点.由纯滚动假设可知，ω不存在z轴分量.

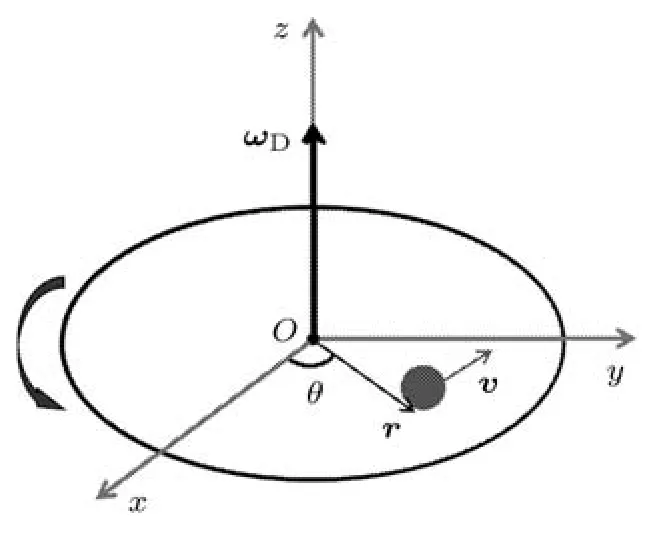
图2 本文所研究系统的坐标系选取及描述其运动的物理量

根据牛顿第二定律和角动量定理，摩擦力作用下的旋转体应满足动力学方程[12-13]

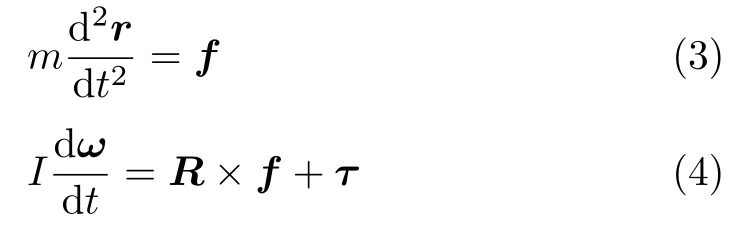
其中，f和τ分别为转盘对旋转体的静摩擦力和滚动摩擦力矩.将式(2)等号两边对时间求导，得

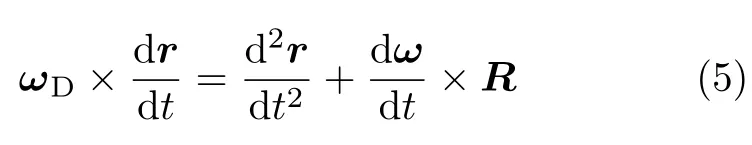
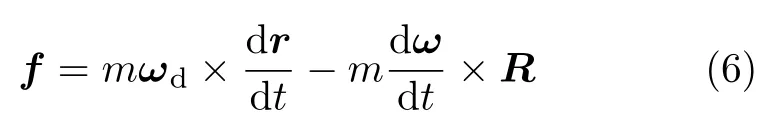
引入无量纲数γ[5]，令

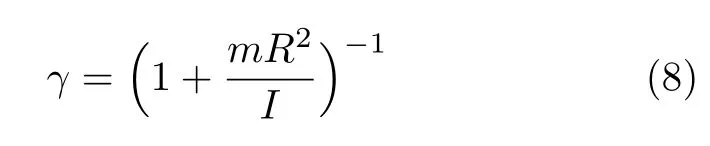
联立式(3)和式(7)，消去f并代入γ可得

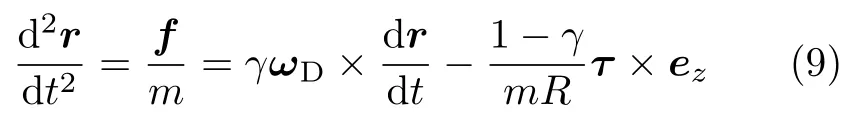
旋转体所受滚动摩擦力矩τ的大小与转盘的压力N成正比[8]，即

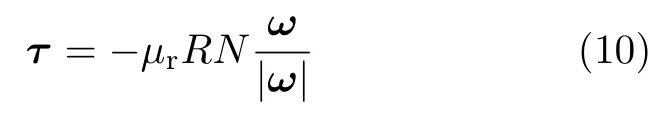
其中µr为描述滚动摩擦的相关系数，由旋转体与转盘表面材质决定；N=mg为转盘对旋转体支持力大小.考虑到柱坐标系下的变换关系[13]

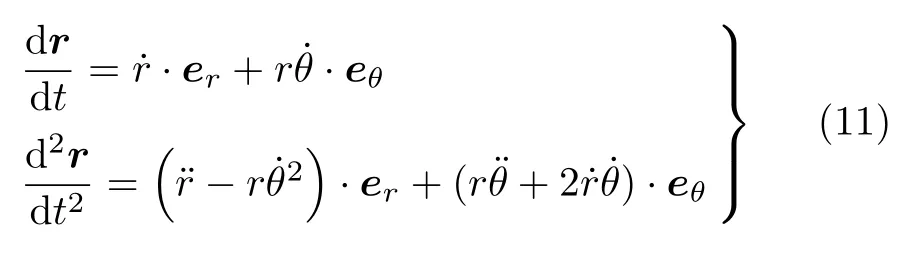
将式 (10)和式 (11)代入式 (9)，由等式两边 er和eθ方向分量分别相等，可得极坐标平面下旋转体满足的微分方程组

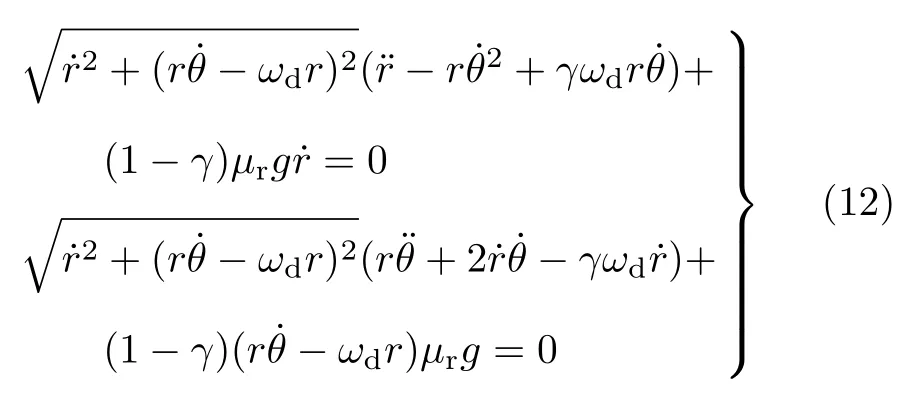
其中r和θ分别为旋转体质心在极坐标系下的极径和极角 (质心相位角).对方程组 (12)进行数值求解，即可得到旋转体在转盘上运动的理论轨迹及其他特征参数.

2 数值模拟与实验

2.1 实验装置

本课题实验选用型号为 2815的航模电机作为驱动转盘转动的动力，供电采用2200mAh直流电池，并用40A电子调速器控制电机速度，以带动直径 40cm 的圆盘水平匀速转动并可实时调节其转速.实验以乒乓球和实心弹性球作为实验对象进行探究.

实验装置如图3(a)所示.实验中，将帧率为30的摄影设备固定在距离转盘中心正上方60cm处拍摄球体的运动.摄影设备已通过网格纸测试以保证所用焦段没有镜头畸变，如图3(b)所示.将所录制视频导入物体追踪软件Tracker进行处理，通过追踪旋转体的运动，即可获得其质心速度等运动参量.

图3

作为本文的一个重要前提假设，当要求球体进入圆盘的质心初速度为0时，初始纯滚动条件可以通过如下方法实现：先使用自制纸槽将球体约束在转盘某一位置随转盘滚动，此时乒乓球在约束点上只存在定点滚动而没有质心初速度.当球体达到稳定滚动后，撤除纸槽，即可达成纯滚动的初始条件.当要求球体进入质心的初速度不为0时，初始纯滚动条件无法达成，小球进入圆盘之后会经历很短一段时间的有滑滚动而后再进入无滑滚动.

球体进入圆盘的质心初速度取值则可通过如下方法获得：利用一个与圆盘正好接触的静止倾斜轨道引导球体滚进转动圆盘；通过改变球体释放高度和滑轨方向，即可大致控制球体质心初始速度大小及方向.精确的初速度大小与方向可通过Tracker读取.

2.2 球体运动模式

通过改变初值条件和参数，借助 Mathematica对方程组(12)进行数值求解，在不考虑空气阻力的情况下，可以从理论上得到4种不同类型的运动模式.

当滚动摩擦不可忽略时，可能存在两种运动模式:

(1)球体做先靠近转盘中心再远离转盘中心的螺旋运动；

(2)球体做远离转盘中心的螺旋运动.

当滚动摩擦可以忽略时，也可能存在两种运动模式:

(1)若球体质心初速度不为0，球体滚动的同时质心做匀速圆周运动；

(2)若球体质心初速度为0，球体做定点滚动，即其质心位置将保持不变.

下面分别对4种运动模式进行实验与理论的对比.使用Tracker测量球体释放时的初始运动参数，将其代入式(12),得到该初始值下的数值解，然后将数值模拟得到的运动轨迹与实验追踪的轨迹进行比较.下面以乒乓球为例进行比较分析，实心球的结果与之类似.实验中用到两种铝盘，一种是表面呈磨砂质感的平整铝盘 (甲型铝盘，滚动摩擦不可忽略)，另一种则是表面经过镜面抛光处理的光滑平整铝盘(乙型铝盘，滚动摩擦系数可视为0).乒乓球与转盘之间的滚动摩擦系数通过拟合乒乓球质心相位角速度曲线得到.实验轨迹与理论轨迹的对比分析如下:轨迹(A) 使用甲型铝盘，滚动摩擦不可忽略.乒乓球可能做先靠近转盘中心再远离转盘中心的螺旋运动，数值模拟和实验对比情况如图4所示.所用参数r0=0.055m,˙r0=−0.139m/s,θ0=4.603rad,˙θ0=0.723rad/s,ωD=15.8rad/s滚动摩擦系数拟合值为µr=0.009，持续时间为5.91s.

轨迹 (B) 使用甲型铝盘，滚动摩擦不可忽略.乒乓球也可能做远离转盘中心的螺旋运动，数值模拟和实验对比情况如图 5所示. 所用参数 r0=0.017m,˙r0=0.079m/s,θ0=−1.959rad,˙θ0=9.058rad/s,ωD=12.0rad/s滚动摩擦系数拟合值为µr=0.009，持续时间为7.98s.

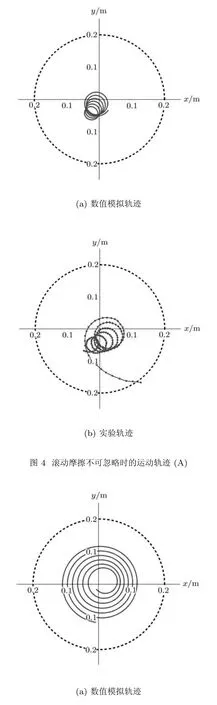
图5 滚动摩擦不可忽略的运动轨迹(B)

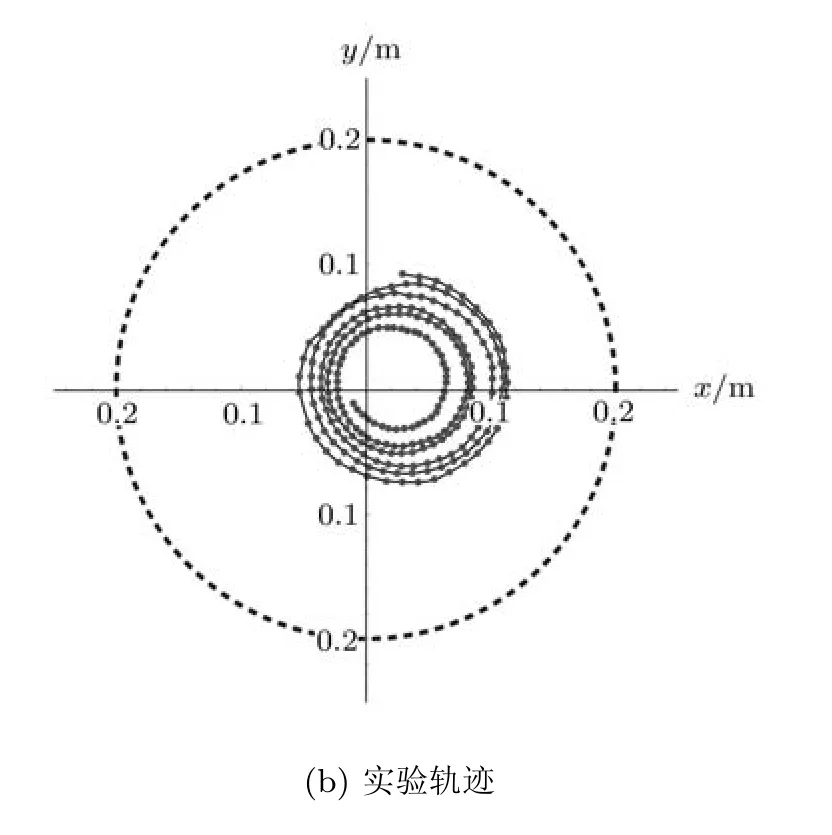
图5 滚动摩擦不可忽略的运动轨迹(B)(续)

轨迹(C) 使用乙型铝盘，滚动摩擦系数视为µr=0.乒乓球进入转盘的质心初速度不为 0，则乒乓球在滚动的同时质心做匀速圆周运动，数值模拟和实验对比情况如图 6所示所用参数 r0=0.080m,˙r0=0.192m/s,θ0=0.476rad,˙θ0=−0.111rad/s,ωD=15.8rad/s,持续时间为2.33s.

轨迹(D)使用乙型铝盘，滚动摩擦系数视为µr=0.乒乓球进入转盘的初始质心速度为0，乒乓球做定点滚动，数值模拟和实验对比情况如图7所示.所用参数r0=0.078m,˙r0=0.001m/s,θ0=0.666rad,˙θ0=−0.000rad/s,ωd=15.8rad/s,持续时间为1.20s.

从图4∼图7可以看出，虽然实验与数值计算结果符合得较好，但仍有3个问题值得讨论：

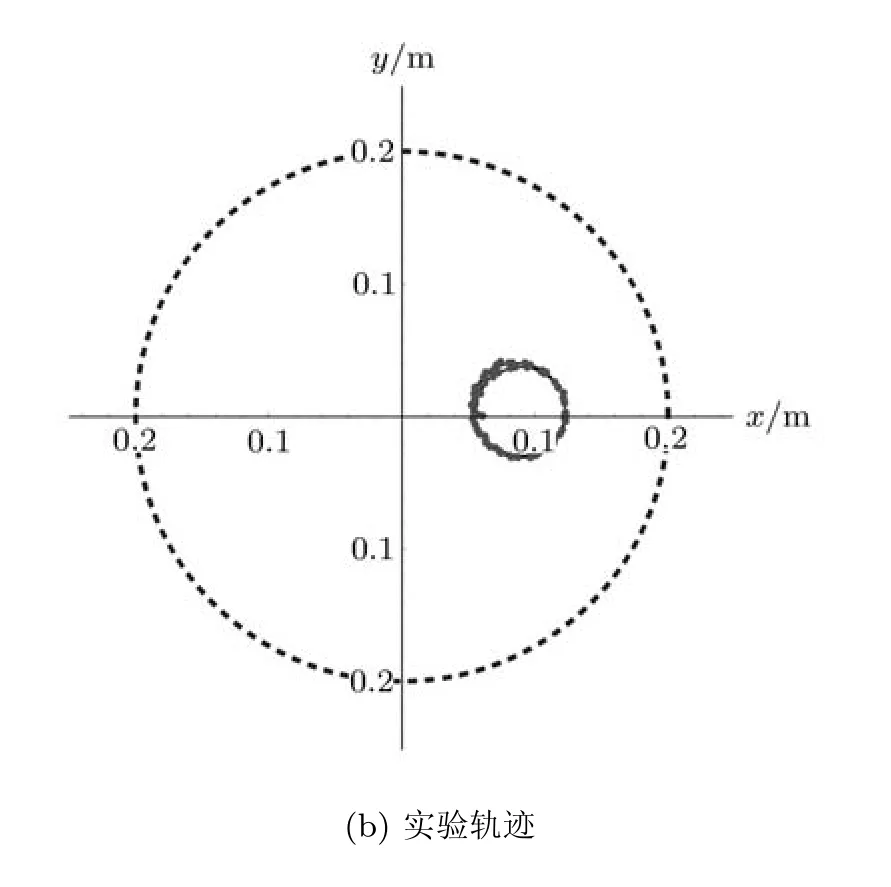
图6 滚动摩擦系数很小时的运动轨迹(C)

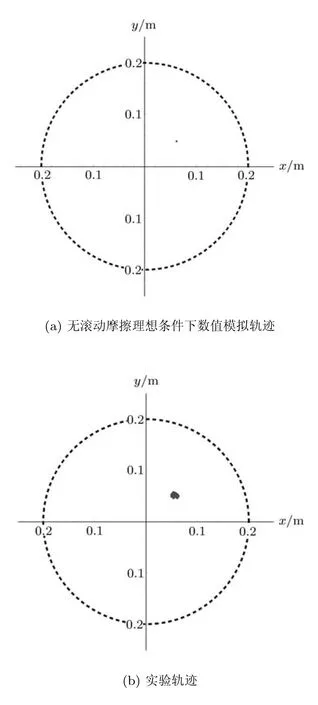
图7 滚动摩擦系数很小时的运动轨迹(D)

(1)从图4可以看出，前期乒乓球的实验轨迹与理论轨迹较为吻合；但在远离转盘中心运动阶段，随着轨迹半径的增大，转盘提供的静摩擦力逐渐不能满足乒乓球做无滑滚动所需的向心力，因此实验中观察到乒乓球出现明显的离心滑动现象，不再满足理论模型中的纯滚动假设，因此乒乓球运动半径逐渐增大并最终被甩出转盘，实验轨迹后段与理论轨迹差别较大.

(2)从图 5可以看出，乒乓球做远离转盘中心的螺旋运动时，实验轨迹的半径小于理论值.这是由于理论计算忽略了空气阻力，而随着螺旋线半径的增大，乒乓球运动线速度增大，空气阻力的影响亦增大.空气阻力使得乒乓球运动线速度小于理论值，离心趋势下降，导致实验轨迹半径比理论预期值偏小.

(3)通过理论计算可知，轨迹(C)和轨迹(D)其实是轨迹 (B)在滚动摩擦系数为 0时的特殊形式.当乒乓球质心初速度不为 0时得到轨迹 (C)，而当乒乓球质心初速度为0时则得到轨迹(D).实验结果与理论预期完全相符.

2.3 质心相位角周期的收敛现象

除了存在多种类型的运动轨迹之外，旋转体质心绕盘运动的角速度，即相位角速度亦存在有趣的现象.Weltner[1]在滚动摩擦可忽略的基础上，从理论上得到了旋转体质心做圆周运动(轨迹(C))时围绕圆心的角速度与转盘旋转角速度的比值恒等于前文所述的无量纲数γ的结论.

本文在理论分析与数值模拟过程中进一步发现：当滚动摩擦不可忽略时，无论旋转体是做先靠近转盘中心再远离转盘中心的螺旋运动(轨迹(A))，还是做远离转盘中心的螺旋运动 (轨迹 (B))，其质心相位角速度 ωθ与转盘旋转角速度 ωD的比值都将收敛于无量纲数γ.

用 Tracker读数并做出实验轨迹 (A)和轨迹(B)的质心相位角速度随时间变化曲线，并与对应的理论曲线相比较，如图8所示.其中，蓝色实线为理论曲线，蓝色虚线为理论预测的角速度收敛极值γωD，红点为实验数据点.从图中可以看到，实验中球体的角速度在γωD附近波动并逐渐收敛，与理论预期符合较好.然而，实验条件无法达到理论模型的理想情况，使得实验曲线和理论曲线存在一定的偏差.图8(a)中，实验曲线相比理论曲线有一个整体的“滞后”，这是由于理论曲线采用的是无滑滚动条件，即从初始时刻起，球体即在转盘上做无滑滚动；而实验中乒乓球在进入转盘的瞬间是不满足无滑滚动的，要经过短时间的弛豫才能达到无滑滚动(该图对应的实验参数条件下，约需0.3s)，由此造成了曲线的整体“滞后”.乒乓球实际还受到一定的空气阻力，并且质心速度越大所受阻力越大，这在理论模型中被忽略了，因此造成了图8(b)中实验曲线的周期比理论值略大且收敛速度低于理论值.最后，由于转盘半径有限，导致乒乓球运动时间较短，未能完全收敛到理论值γωD即被甩出转盘.尽管如此，实验曲线的特征与收敛趋势仍然与理论曲线一致.由此，可以将本文提出的这一新发现与文献[1]的结论统一为：匀速水平转动圆盘上的旋转体无论做何种运动，其相位角周期都必将收敛于极限值2π/γωD.

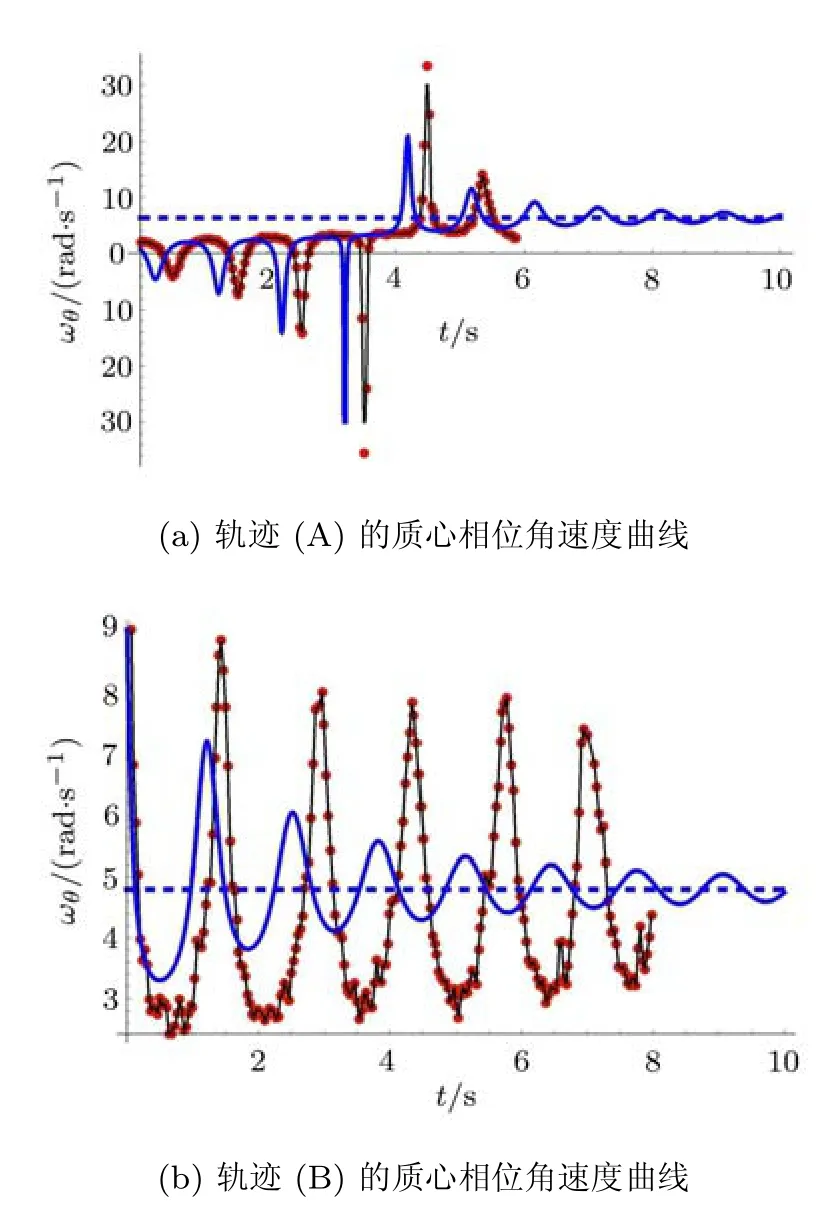
图8

为了进一步验证这一新发现，本文针对旋转体做向外螺旋运动(轨迹(B))的情况，测量并验证转盘以不同角速度 ωD转动时，旋转体稳定运动的相位角速度ωθ符合理论预测公式ωθ=γωD.实验中采用摩擦系数较大的橡胶圆盘作为实验转盘，并选用实心的橡胶球作为旋转体.这是因为实心橡胶球质量远大于乒乓球，受到空气阻力影响较小，而且橡胶球表面摩擦系数更大，更加符合达成轨迹B所需的滚动摩擦系数较大的前提条件.

橡胶球质心相位角速度与转盘转动角速度的实验数据与拟合曲线如图 9所示. 由于实验中橡胶球的角速度时刻发生变化，因此在测量时选取橡胶球到达转盘边缘前最后三个周期内的角速度数据，计算其平均值(图中红色星号)与不确定度(图中误差棒)，并将 (ωD,ωθ)数据以正比例函数为目标函数进行拟合.从图中可以看出，数据拟合度很高 (0.9931)，且拟合得到的 γ值(直线斜率)为0.2848，与实心球体的理论 γ值 =0.2857的相对误差仅为0.32%.可见，实验结果与理论预测符合得很好.

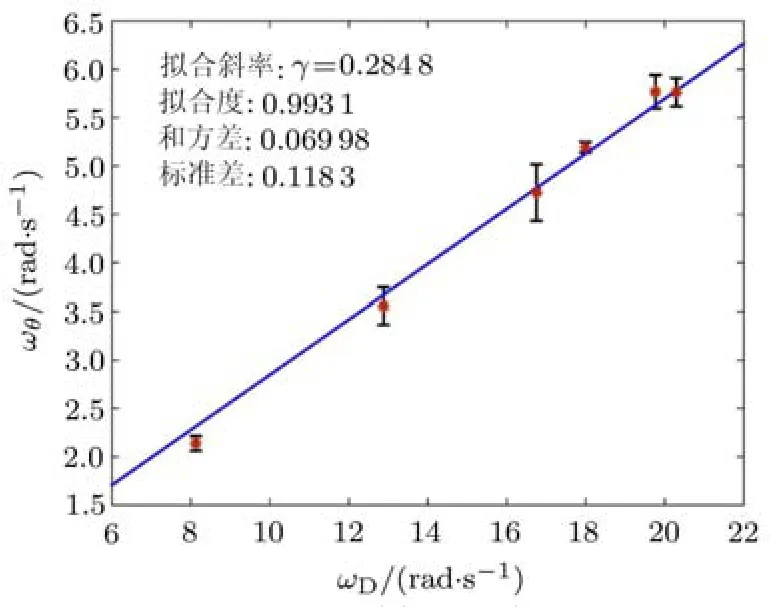
图9 橡胶球质心相位角速度与转盘转动角速度数据拟合图

3 总结与讨论

本文研究了匀速转动圆盘上轻质旋转体的运动轨迹，在纯滚动假设前提下，得到描述旋转体运动的微分方程组，而后利用Mathematica进行数值求解，预测了4种不同的运动轨迹，并在实验中一一再现.课题组还发现，当滚动摩擦不可忽略时，无论旋转体处于何种运动模式，其质心相位角速度与转盘角速度的比值都将收敛于无量纲数γ.此结论对现有文献的理论分析结果进行了扩展，并通过多组实验进行了拟合验证，是本文的一个重要发现.该发现可以为测量球类物体转动惯量提供一种新的思路和方法.

然而，本文的研究仍存在不足：(1)实验发现旋转体的滚动角速度有微小的z轴分量，不能完全满足纯滚动假设，这点本文并未加以考虑；(2)不能准确判断旋转体在何种条件下将出现有滑滚动；(3)轨迹 (A)与轨迹 (B)的出现条件与旋转体运动参量的初值、转盘角速度、旋转体质量、转动惯量皆有关系，本文并未分别探究具体的阈值区间；(4)对于质量较轻的球体(如乒乓球)，空气阻力造成的影响会随着质心速度的增大趋于明显，并不能完全忽略.课题组将在后续工作中加以改进.

1 Weltner K.Stable circular orbits of freely moving balls on rotating discs.Am J Phys,1979,47(11):984-986

2 Burns JA.Ball rolling on a turntable:Analog for charged particle dynamics.Am J Phys,1981,49(1):56-58

3 Voyenli K,Eriksen E.On the motion of an ice hockey puck.Am J Phys,1985,53(12):1149-1153

4 Weltner K.Central drift of freely moving balls on rotating disks:A new method to measure coefficients of rolling friction.Am J Phys,1987,55(10):937-942

5 Gersten J,Soodak H,Tiersten MS.Ball moving on stationary or rotating horizontal surface.Am J Phys,1992,60(1):43-47

6 Sokirko AV,Belopolskii AA,Matytsyn AV,et al.Behavior of a ball on the surface of a rotating disk.Am J Phys,1994,62(2):151-156

7 Ehrlich R,Tuszynski J.Ball on a rotating turntable:Comparison of theory and experiment.Am J Phys,1995,63(4):351-359

8 Soodak H,Tiersten MS.Perturbation analysis of rolling friction on a turntable.Am J Phys,1996,64(9):1130-1139

9 Weckesser W.A ball rolling on a freely spinning turntable.Am J Phys,1997,65(8):736-738

10 M´unear HA.A ball rolling on a freely spinning turntable:Insights from a solution in polar coordinates.Lat Am J Phys,2011,5(1):49-55

11 Agha A,Gupta S,Joseph T.Particle sliding on a turntable in the presence of friction.Am J Phys,2015,83(2):126-132

12 姜芳,赵东.纯滚动圆轮静摩擦力方向的确定. 力学与实践,2011,33(1):86-88

13 蔡积仁.浅谈滚动摩擦.物理通报,2006(2):37-39

14 李书民.经典力学概论.合肥：中国科学技术大学出版社,2007

O313.3,O311.2,O313.5

A

10.6052/1000-0879-16-348

2016-10-24收到第1稿，2017-01-02收到修改稿.

1)穆翔栩，四川大学物理科学与技术学院2015级物理学类本科生.

2)林方,指导教师,通迅作者.E-mail:linfang@scu.edu.cn

穆翔栩,关国业,张博文等.轻质旋转体在水平匀速转动圆盘上的多种运动模式.力学与实践,2017,39(5):523-529

Mu Xiangxu,Guan Guoye,Zhang Bowen,et al.Varied motion modes of light objects rolling on a horizontally rotating disk.Mechanics in Engineering,2017,39(5):523-529

(责任编辑:胡 漫)