变刚度梁挠度曲线的Green函数法求解
2017-11-22刘胜来
刘胜来
(清华大学土木工程系,北京100084)
变刚度梁挠度曲线的Green函数法求解
刘胜来1)
(清华大学土木工程系,北京100084)
在变刚度梁的线弹性问题中,求解梁受静力荷载的挠度曲线常用解法有积分法与单位荷载法.本文从变刚度梁挠度曲线的微分方程出发,给出了变刚度梁挠度曲线的Green函数法解答,并分析了该解法的优点.从推导结果可以看到,本文提出的公式具有统一、精确、简洁、适合电算的特点,在编制杆系结构计算软件中将具有重要应用价值.
变刚度梁,挠度曲线,Green函数法
线弹性小变形下梁的弯曲变形问题是材料力学中一个常见问题,它的挠度曲线用微分方程可以表示为
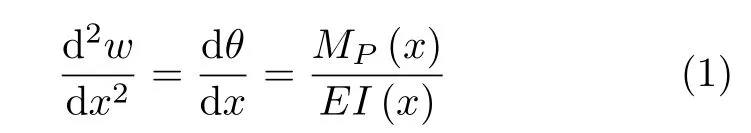
其中 w为横向位移,θ为转角,MP(x)为弯矩,EI(x)为弯曲刚度.
1 积分法和单位荷载法
一般地,梁的挠度曲线方程可以直接从式(1)积分求得
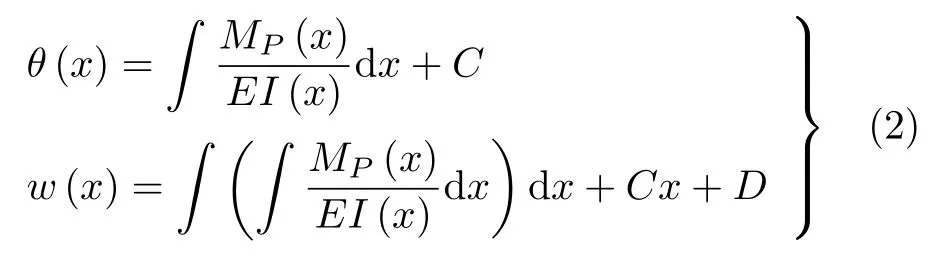
式中C和D是积分常数,需要通过边界几何约束条件予以确定.如果是等刚度梁,式(2)中弯曲刚度EI还可以提到不定积分号外.
值得注意的是,若梁是变刚度的,也即EI(x)不是一个常数,而是用一个复杂解析函数表示,上述不定积分的解不一定能获得初等函数表达式[1],同时不定积分计算一般较为繁琐,并不利于编程计算,通过式(2)积分求解挠度曲线存在不少实际操作上的困难.
一个朴素的思想是对弯矩函数 MP(x)和弯曲刚度EI(x)做多项式插值,使上述被积函数为有理函数,不定积分一定可以用初等函数表示[1].然而这样不仅计算复杂,而且多项式插值在模型中又引入了插值误差,对挠度曲线的求解精度造成了损失,还不容易进行误差估计.
文献[2]通过拉氏变换求解梁的挠度曲线,得到了一种新的计算梁的挠度曲线方式,该方法在梁受分段分布荷载时较为简便,但该方法受限于弯矩函数为多项式和弯曲刚度为常数的假设,其导出的挠度曲线公式与直接积分差别不大.
考虑用无量纲载荷法计算上述梁的挠度曲线,不妨虚设单位载荷作用在梁的xa处,由力的平衡容易得到虚设单位载荷下弯矩函数为
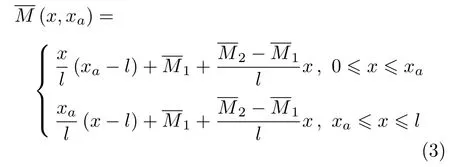
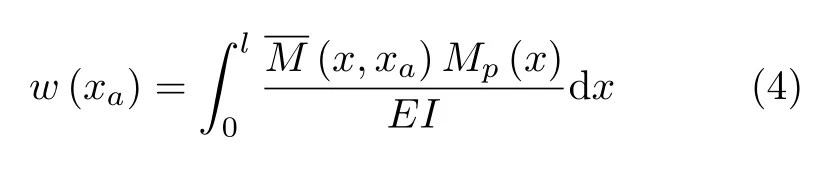
另外,由于积分法和单位载荷法均是基于微分方程(1)的精确求解方法,因此它们的计算结果必然是一致的[3].
2 Green函数法
考虑式(1)表示的变刚度梁的弯曲变形挠度曲线求解问题,不妨令边界条件为
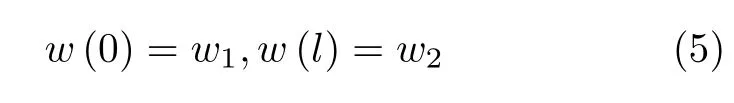
微分方程(1)中的算子可以记作

由文献 [3]结论,上述微分算子对应的 Green函数为
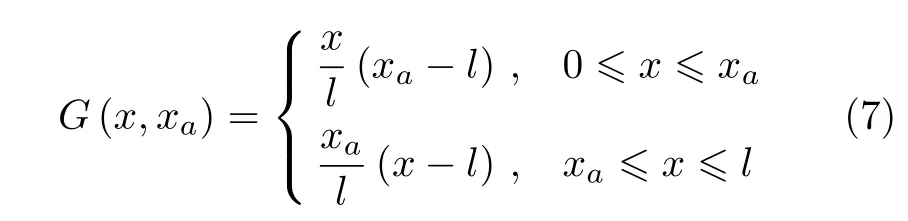
其中xa为梁中任一点坐标.式(7)满足
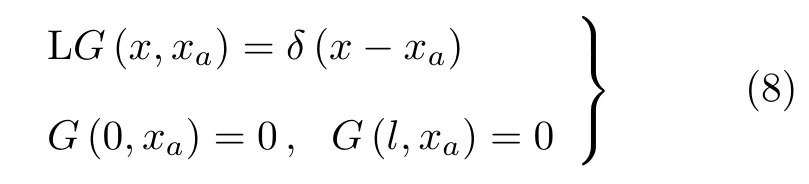
其中δ(x)为狄拉克函数[5].
由Green函数性质,变刚度梁的挠度曲线函数可写为
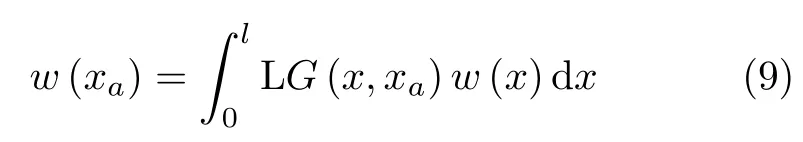
将式(9)分部积分,有
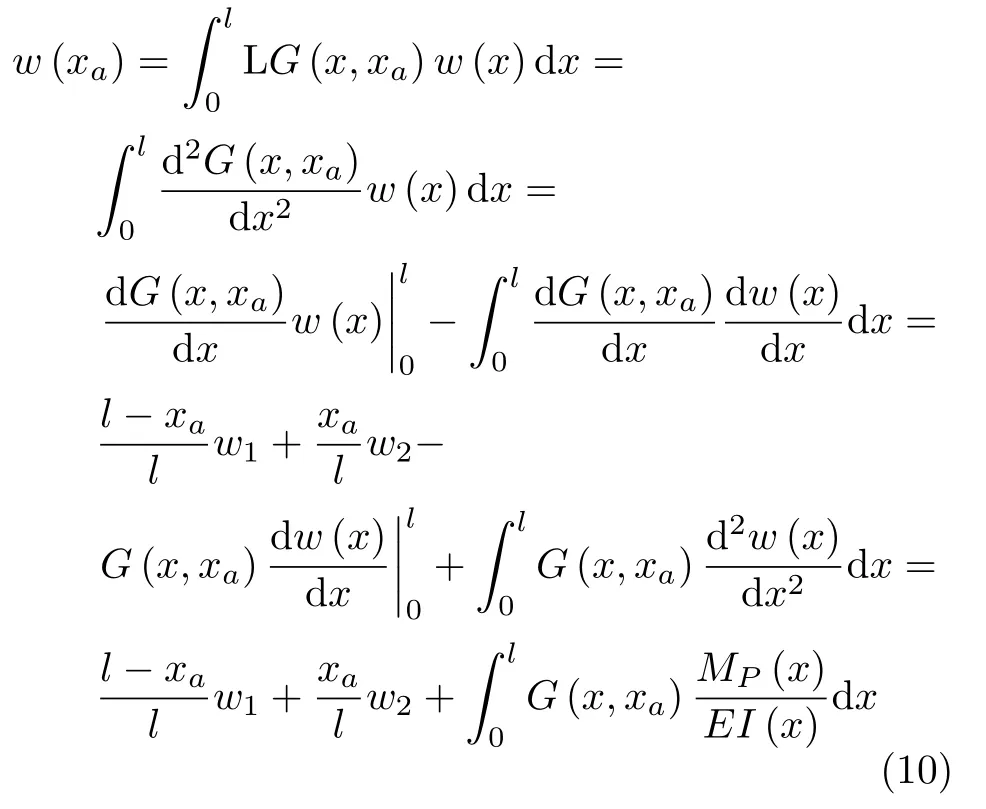
将式 (7)代入式 (10),得变刚度梁挠度曲线的解析式为
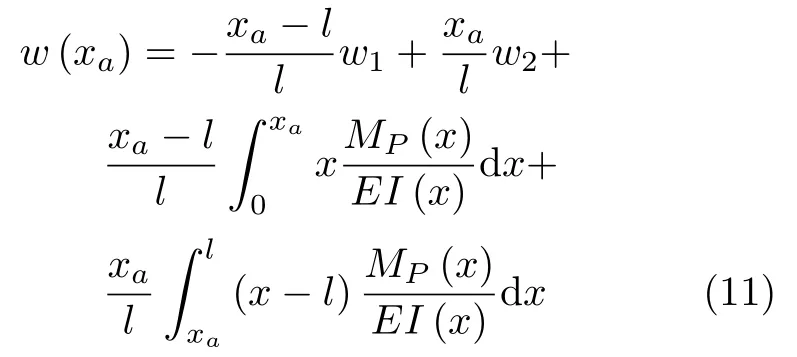
直接对式(11)求导可得
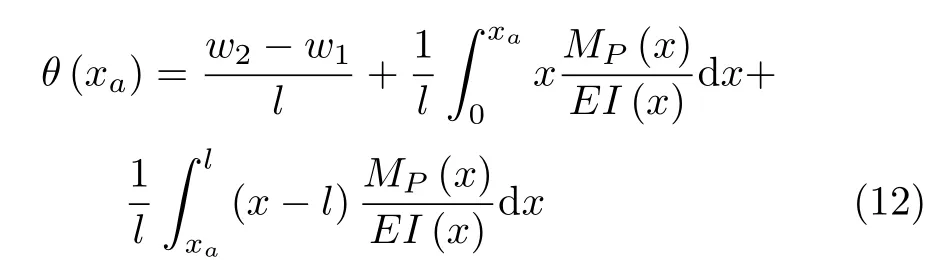
式(11)和式(12)即为Green函数表示的变刚度梁挠曲线和转角的计算公式.
比较式 (2)和式 (11)两种解答的格式可以看到,Green函数法得到的式(11)更具优势.不同于积分法式(2)中挠度曲线需要求不定积分,式(11)挠度曲线的解为定积分形式,在求解任一点位移值时可采用数值积分法求得任意精度的数值解,无需考虑被积函数积分后能否表示成初等函数形式,当MP(x)/(EI(x))形式较复杂或梁上载荷分段分布时,仍能采用统一的式(11)求解.基于这点,式(11)所示的定积分形式解还适合用于统一的工程计算软件的程序编制,最后求解的积分精度取决于数值积分方法选取点数,求解误差可控.当然,式(11)所示定积分形式解也存在一定缺点,如在计算每点挠度均需分别计算数值积分,实际使用时通常可以采用在梁上先求足够数量点的挠度,再做多项式插值来替代.
对比式 (4)和式 (11)可以发现当梁两端简支时,Green函数法导出的式(11)事实上等价于单位载荷法.但单位载荷法计算挠度曲线和转角需要设置两个不同的单位载荷并分别进行分析,Green函数法计算挠度与转角的式(11)和式(12)是形式统一的,对挠度直接求导即得转角的计算公式,这相较单位载荷法显得更为简洁.
3 Green函数法的一个改进
从式 (11)可以看到,利用式 (11)计算梁挠度曲线的一个前提是需要弯矩函数 MP(x)较容易求得,而在分布载荷尤其是分段分布载荷作用时,弯矩函数MP(x)是不易求解的,这使得式(11)在计算复杂类型载荷时存在一定困难,且不易应用于电算的程序编制.
考虑梁的平衡方程
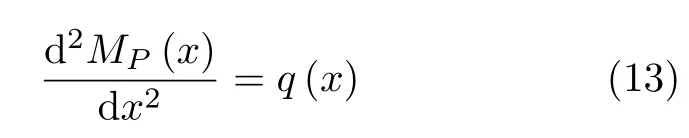
边界条件设为
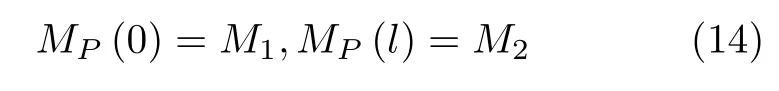
对比式 (13)与式 (1),易知其对应的微分算子是相同的,边界条件也类似,直接类比式(11)推导结果,可得弯矩函数为
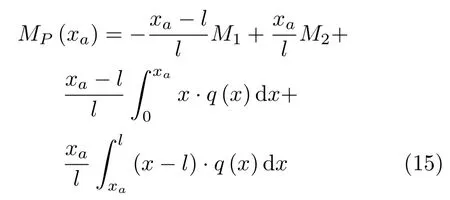
直接求导可得剪力函数为
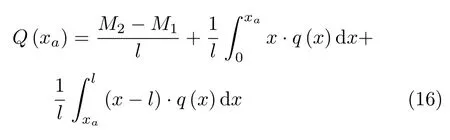
可以看到,上式中对分布载荷q(x)没有特别限制,即使是分段分布载荷、复杂函数形式载荷均可通过数值积分计算.式(15)使得式(11)计算公式的适用范围更加广泛.
通过式(15)先计算弯矩函数MP(x),再通过式(11)计算挠曲线方程,将变刚度梁挠度曲线计算过程划分为两步.如果在用式(15)计算弯矩函数时使用数值积分,将给挠度曲线计算带来中间误差,不过该中间误差仅存在于式(11)被积函数的分子项中,误差控制较为容易.
当梁两端简支时,由边界条件可得

当梁为悬臂梁也即一端固支一端自由时,边界条件为
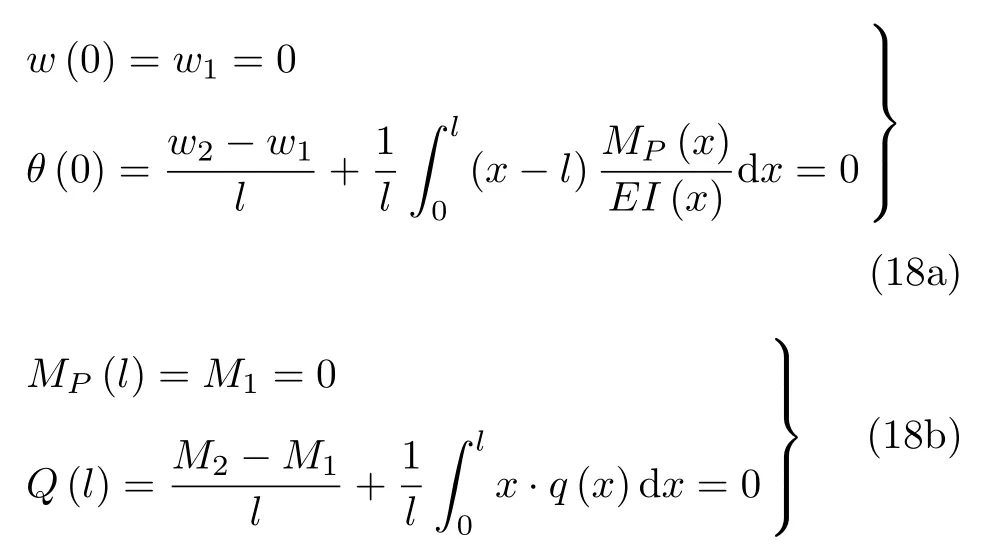
先由式 (18b)解出 M1和 M2,进而由式 (15)求得MP(x)的表达式,代入式(18a)求得w1和w2.
当梁两端固支时,边界条件为
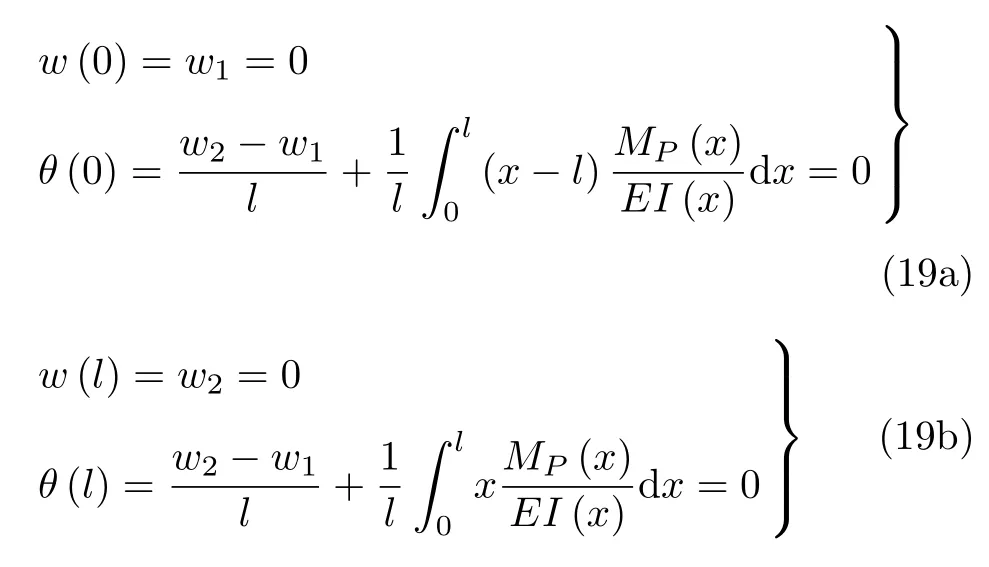
求出w1,w2,M1和M2.
此外,对于支座位移等复杂边界条件,可类似上述方法先求得未知量w1,w2,M1和M2,再代入式(11),式 (12),式 (15)和式 (16)得到对应边界条件下各物理量的计算公式,因此它们对不同边界条件的变刚度梁均是适用的.
4 一个特例——等刚度梁
事实上,当梁的弯曲刚度为常数时,上述梁的挠度曲线公式(11)和式(15)还可以归结为一个公式.结合式(1)与式(13),可得
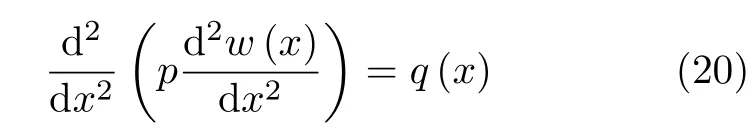
其中p=EI(x),是常量.该微分方程的算子记作
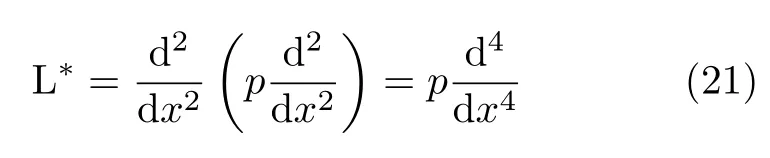
当梁两端简支时,边界条件为
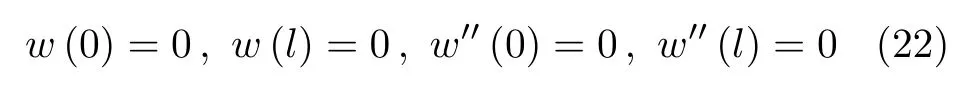
由文献[3]中Green函数定义,微分算子L∗对应的Green函数需满足
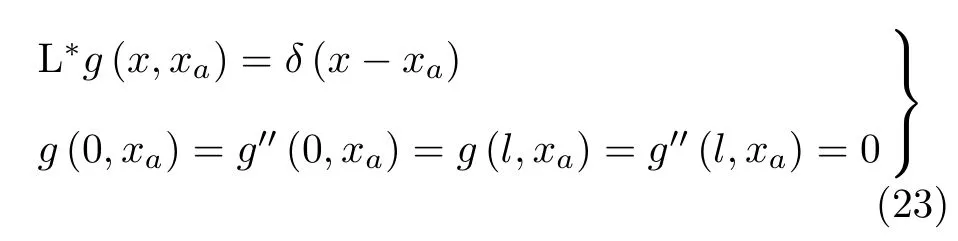
式(23)等价于下面3个条件:
① g(x,xa)连同其一、二、三、四阶导数在x/=xa时,都是 x的连续函数,满足非齐次方程L∗g(x,xa)=0;
②满足边界条件
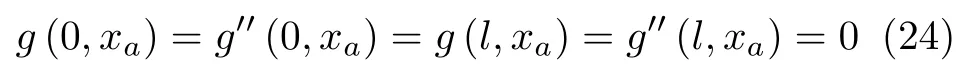
③g(x,xa)在正方形 0≤x≤l,0≤xa≤l上是二阶连续的,且[pg′′(x,xa)]′看作 x的函数时,在x=xa处具有第一类间断,其跃度为1,即
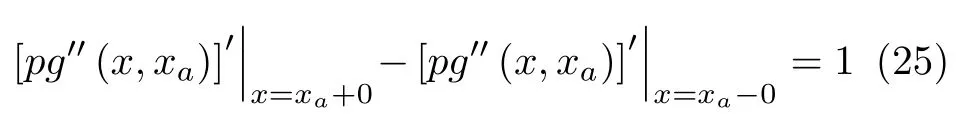
由上述 3个条件可以构造该微分算子对应的Green函数为由Green函数性质,有
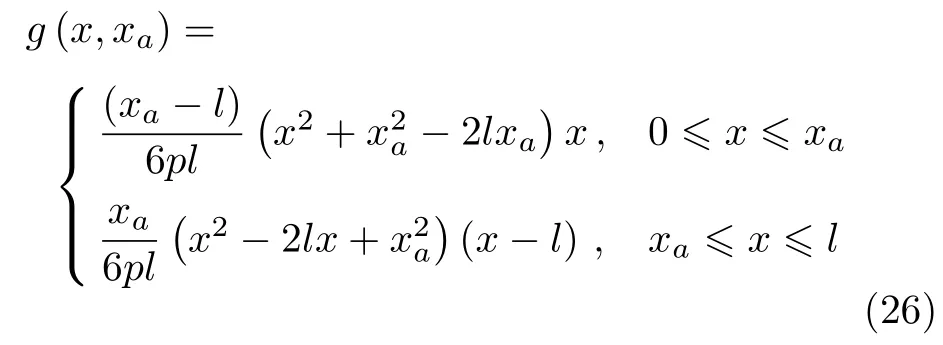

将式(26)代入式(27),即得弯曲刚度为常数时挠度曲线的表达式
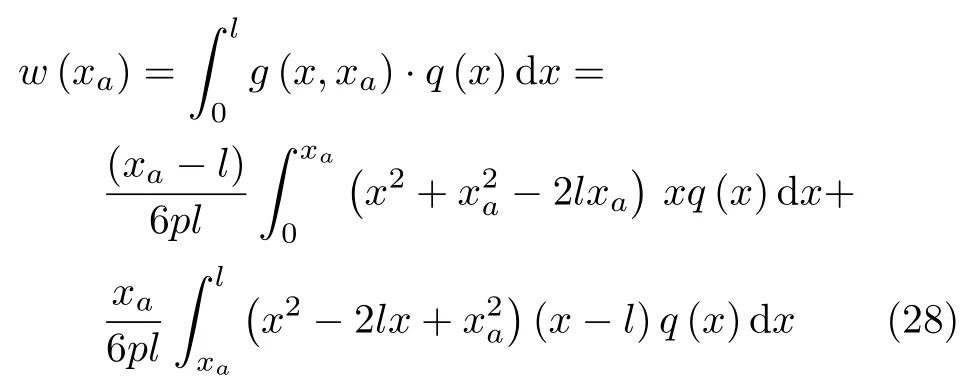
式 (28)等价于式 (11)和式 (15)分两步计算的结果,可以直接将式(15)代入式(11)推导得出.
类似地,当梁一端固支一端自由时,边界条件为
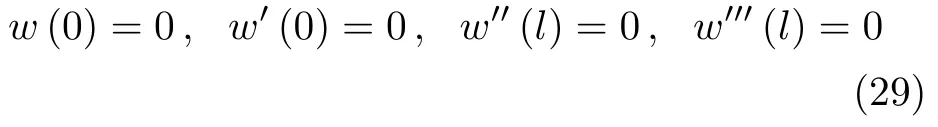
对应的Green函数满足
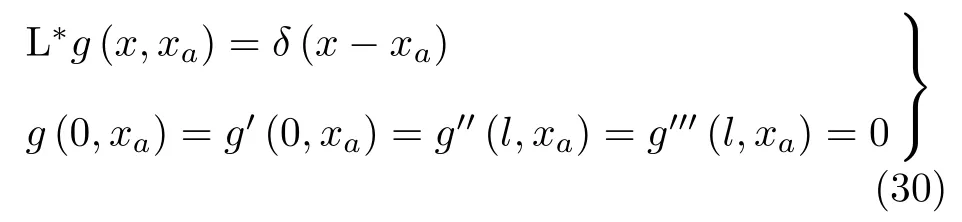
可求得Green函数表达式为
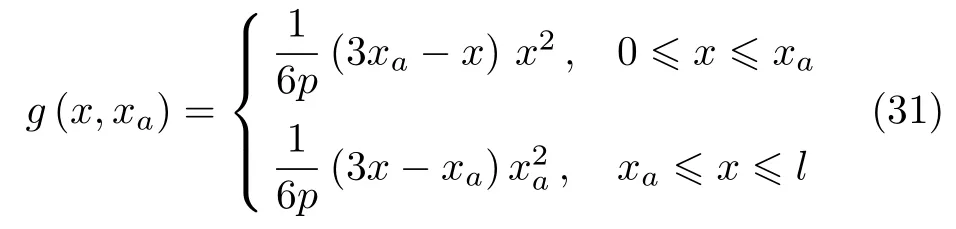
当梁两端固支时,边界条件为
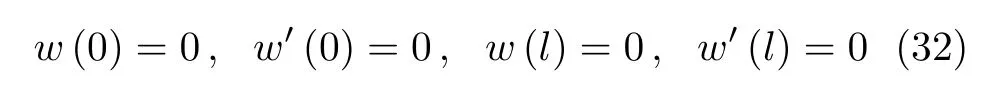
对应的Green函数满足
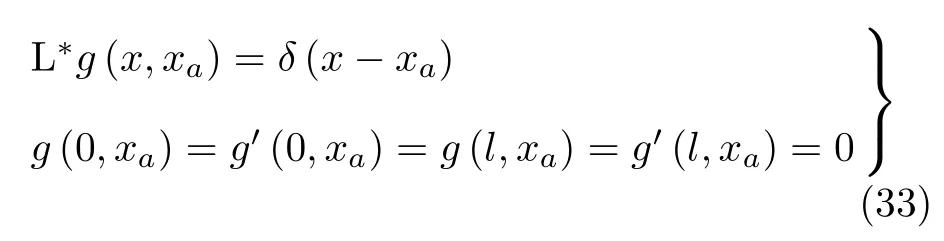
可求得Green函数表达式为
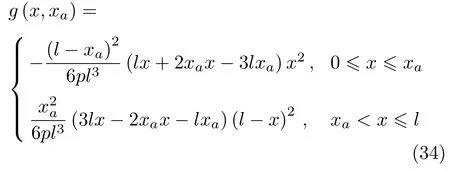
将式(31)和式(34)代入式(27)可分别求得悬臂梁和两端固支梁在弯曲刚度为常数时的挠度曲线.
5 结论
本文基于求解微分方程的Green函数法推导了变刚度梁挠度曲线公式.Green函数法将微分方程的解归结为定积分的形式,对不同边界条件下变刚度、受复杂载荷梁的挠度曲线求解均适用,且直接求导即可得转角计算公式,具有形式统一、简便、精度好等特点,在杆系结构计算软件的编制中有重要应用价值.
1 陈天权.数学分析讲义.第一册.北京:北京大学出版社,2009
2 刘明超,丁晓燕.拉氏变换求解梁的挠曲线方程.力学与实践,2012,34(2):78-80
3 郭孟武.积分法与单位载荷法一致性的数学推证.力学与实践,2013,35(4):70-72
4 彼得罗夫斯基.偏微分方程讲义.段虞荣译.北京:人民教育出版社,1978
5 吴崇试.数学物理方法.北京:北京大学出版社,2003
SOLUTION OF DEFLECTION CURVE OF VARIABLE STIFFNESS BY GREEN FUNCTION METHOD
LIU Shenglai1)
(Department of Civil Engineering,Tsinghua University,Beijing 100084,China)
In the problem of linear elasticity of variable stiffness beam,the solution of the deflection curve of static load is usually obtained by integral method or unit-load method.Based on the differential equation of the problem,this paper gives a new type of solution with Green function method to get the deflection curve of the variable stiffness beam.It can be seen from the derivation results that the formulas proposed in this paper have the characteristics of uniformity,accuracy,simplicity and suitable for computerization,which will have important application value for the analysis of the frame structure.
variable stiffness beam,deflection curve,Green function method
O342
A
10.6052/1000-0879-17-093
2017-03-22收到第1稿,2017-05-19收到修改稿.
1)刘胜来,硕士研究生,主要从事结构工程与计算力学的研究.E-mail:liusl1992@sina.com
刘胜来.变刚度梁挠度曲线的Green函数法求解.力学与实践,2017,39(5):445-448 Liu Shenglai.Solution of de fl ection curve of variable sti ff ness by Green function method.Mechanics in Engineering,2017,39(5):445-448
(责任编辑:胡 漫)
