Trefftz有限元法的研究进展

王克用 李培超

(上海工程技术大学机械工程学院，上海201620)

Trefftz有限元法的研究进展

王克用1)李培超

(上海工程技术大学机械工程学院，上海201620)

Trefftz有限元法(Trefftz finite element method,TFEM)是一种高效的数值计算方法，兼有传统有限元法和边界元法的诸多优点.基于双独立插值模式，结合杂交泛函和高斯散度定理，推得仅含边界积分的有限元格式.简述了过去10年间(2007—2016)Trefftz有限元法在单元域内插值函数、源项处理、特殊功能单元以及非各向同性材料等方面的研究进展，并对未来的发展趋势给出了几点展望.

Trefftz有限元法，域内插值函数，边界积分，特殊功能单元，无源化处理

引言

Trefftz方法是求解偏微分方程的高效数值方法之一，它是以德国数学家Erich Trefftz(1888-1937)的名字命名的，以纪念他在数学领域的开创性贡献，但在当时并未引起广泛重视.在分析网格畸变对薄板单元的影响时，Jirousek等[1]于 1977年首次提出了杂交Trefftz有限元模型.该模型在单元内部和边界上假设两套独立的位移场：单元域内场和网线场.单元域内场可认为是Trefftz有限元法区别于传统有限元法的重要标志，其插值函数(常称为Trefftz函数)精确满足问题的控制方程.相邻单元通过网线场在某种杂交意义上关联成离散的有限元模型.为了推动Trefftz方法在计算力学领域的发展及应用，自1996年开始，每3年召开一次国际会议，报道Trefftz方法的最新进展及研究成果.表1列出了历届Trefftz方法国际会议情况.基于Trefftz方法的数值方法主要包括Trefftz有限元法[23]、Trefftz边界元法[2,4]以及Trefftz无网格法[57]，其详细论述可参见相关著作[2-3,5-6].

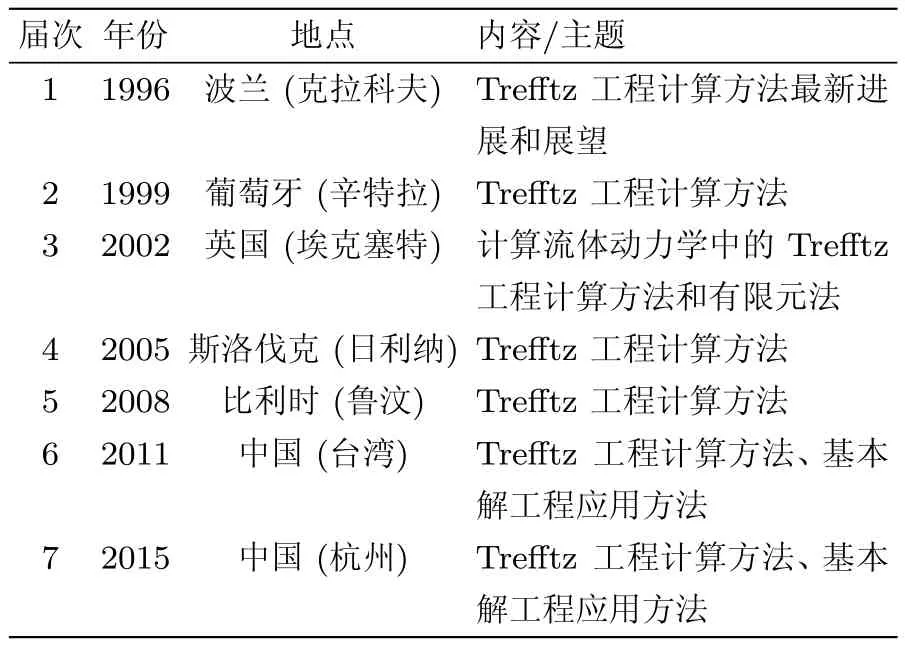
表1 历届Trefftz工程计算方法国际会议

与传统有限元法相比，Trefftz有限元法的显著优势表现在以下几个方面：

(1)单元刚度方程仅涉及边界积分，这样可对曲线或多边形几何边界进行建模[29]，同时也使得Trefftz单元对网格畸变不敏感[1012]，降低了求解维数，从而减小了计算量.

(2)单元域内插值函数无需精确满足单元间的连续性，而是通过变分泛函使之近似满足[1316].

(3)通过寻求局部解函数构造域内插值函数，可捕捉不连续载荷、裂纹、孔洞、夹杂等局部效应问题[2-3,17].

经过40年的发展，Trefftz有限元法已经从平面弹性问题、板弯曲问题、位势问题、压电问题等领域拓展到一些新领域，如牛顿流体的流动问题以及软组织[1819]或水饱和多孔介质问题[2022].本文仅简述过去十年来(2007-2016)Trefftz有限元理论的研究进展.

1 单元域内插值函数的构造原理

Trefftz有限元法在单元域内和单元边界上假定两套独立的场函数插值模式 (图 1).单元域内场可表达为

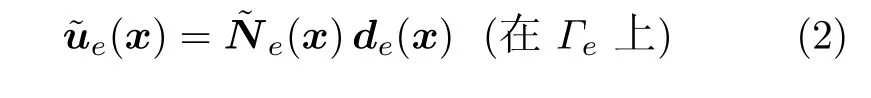
式中，Ωe为Γe围成的单元区域，ˇue为控制方程中源项诱发的特解，ue和˜ue分别为单元域内和边界上的场变量，Ne为 Trefftz插值函数，是控制方程的齐次解，˜Ne为网线插值函数，可按传统有限元方法构建，ce和de分别为待定参数和单元节点自由度列阵.m为截断的完备解或基本解虚源点的个数.

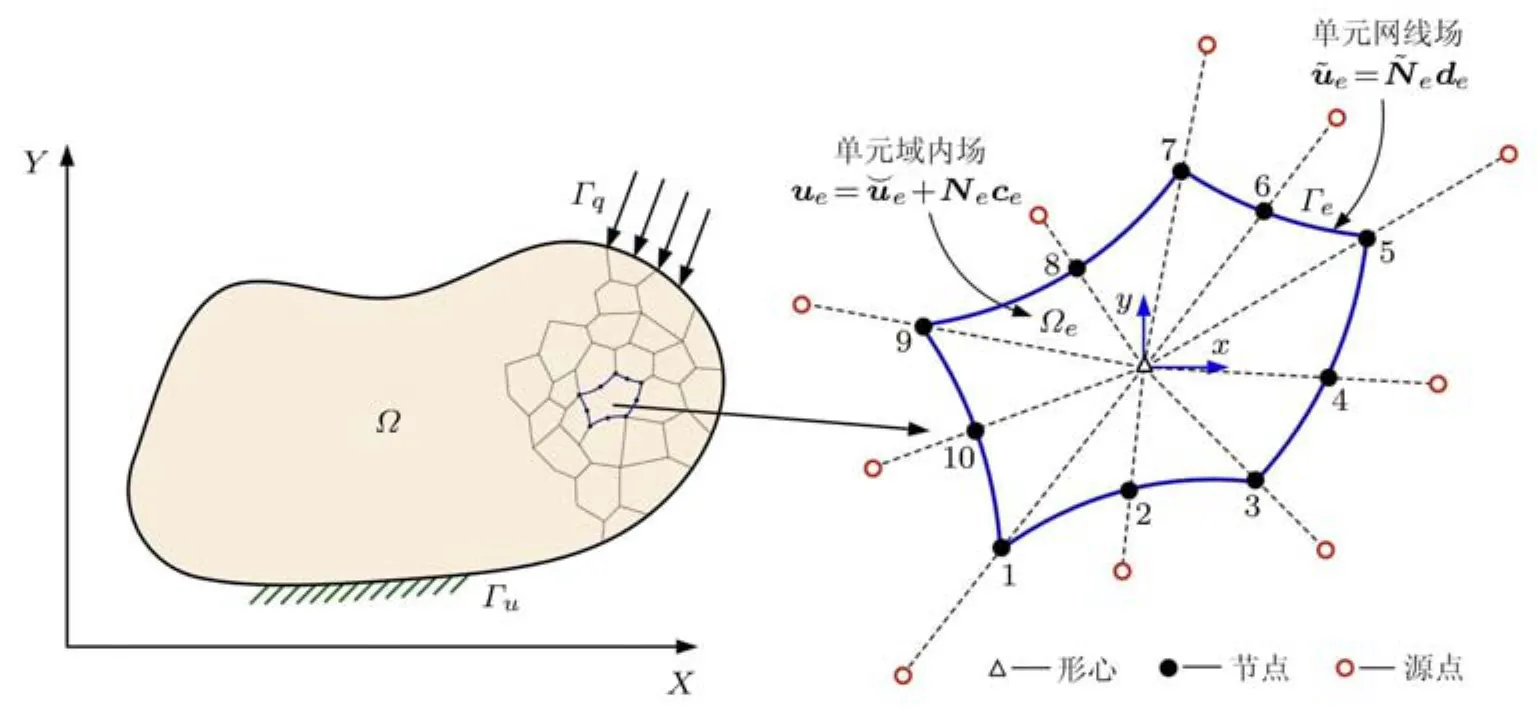
图1 基本解Trefftz单元及其源点

在Trefftz有限元理论中，基本形成了基于完备解和基本解的两种单元构造方法，所构造的单元可分别称为完备解单元和基本解单元.完备解单元出现得较早，其严格的数学理论是由Herrera及其合作者完成的[2326].满足控制方程的完备解系有无穷多项，在构建域内插值函数时，需要适当截断而得到有限项(亦称Trefftz项数)[2].为了避免出现零能模式并使单元性能稳定，用来构建Ne的截断完备解个数必须满足不等式m≥nd−nr，这里nd和nr分别为单元节点自由度和刚体运动模式的数目.值得注意的是，此不等式是一个必要但非充分的条件.一般地，Trefftz项数取最小值并不能保证单元刚度矩阵满秩.在实际应用中，通常需要选取更多的Trefftz项数以确保所构造的单元性能稳定，但另一方面项数过多又会导致数值溢出或者病态系数矩阵.因此，针对不同的工程和物理问题，需要数值验证确定合理的 Trefftz项数.Choo等[11]利用 Mindlin-Reissner厚板问题解构造出 9自由度三角形 (T32-7)和12自由度四边形(Q32-11)板弯曲单元，当这两种单元退化到薄板极限情形下不会出现自锁现象.Moldovan等[20]基于Biot理论，利用Navier控制方程的自由场解构造域内试函数，从而建立了饱和多孔介质的杂交Trefftz应力元和位移元模型.Wang等[12]从准调和多项式出发，推得轴对称位势问题的完备解插值函数，并构造了4节点四边形轴对称环状单元.Rezaiee-Pajand等[27]分析了薄板弯曲问题，并构造了两种高阶杂交Trefftz单元：三角形单元(THT-15)和四边形单元(QHT-23).为了更好地兼容，采用3节点Euler-Bernoulli梁的形函数构造网线函数.

由于很难得到一些工程和物理问题的完备解，且截断Trefftz项数时需要格外小心，才能达到预期精度.为了克服这一缺点，基本解 Trefftz单元应运而生[28].尽管基本解Trefftz单元采用与传统边界元法相同的基本解形式，但二者有本质区别.根据互易定理，传统边界元法涉及边界积分方程，在处理奇异或超奇异积分时会遇到困难，而基本解Trefftz单元因不涉及边界积分方程完全不受其限.基于杂交Trefftz有限元思想，Qin[2]和 Wang等[28]最早提出了基于基本解的Trefftz有限元模型，并成功应用于二维单层和多层材料的热传导分析中.随后，利用基本解Trefftz有限元法，Wang等[29]分析了正交各向异性平面弹性问题.Cao等[30]利用格林函数形式的基本解作为域内插值函数分析了平面压电问题，并且对应力集中现象提出了一些新见解.Wang等[13]分析了 Poisson-Boltzmann方程和扩散反应方程等两类二维Dirichlet问题.首先在通过每个Picard迭代步引入虚拟项，冻结 Poisson方程涉及的非线性项，然后利用仅含边界积分的基本解Trefftz有限元模型进行求解.为建立基本解单元列式，需在单元域外设置若干虚拟的源点[31]，利用源点和单元节点的坐标信息计算基本解，进而构建域内插值函数.与完备解方法类似，虚拟源点的最优数目也需要通过数值算例验证.但Wang和Qin建议，采用与单元节点相同数目的虚源点能够保证求解精度.由于大多数工程和物理问题的基本解已获知，因此基于基本解构建域内插值函数的方法十分便捷.表2列出了基于完备解和基本解构造Trefftz插值函数的相关情况对比.另外，关于基本解Trefftz有限元法的综述文献可参见文献[32].

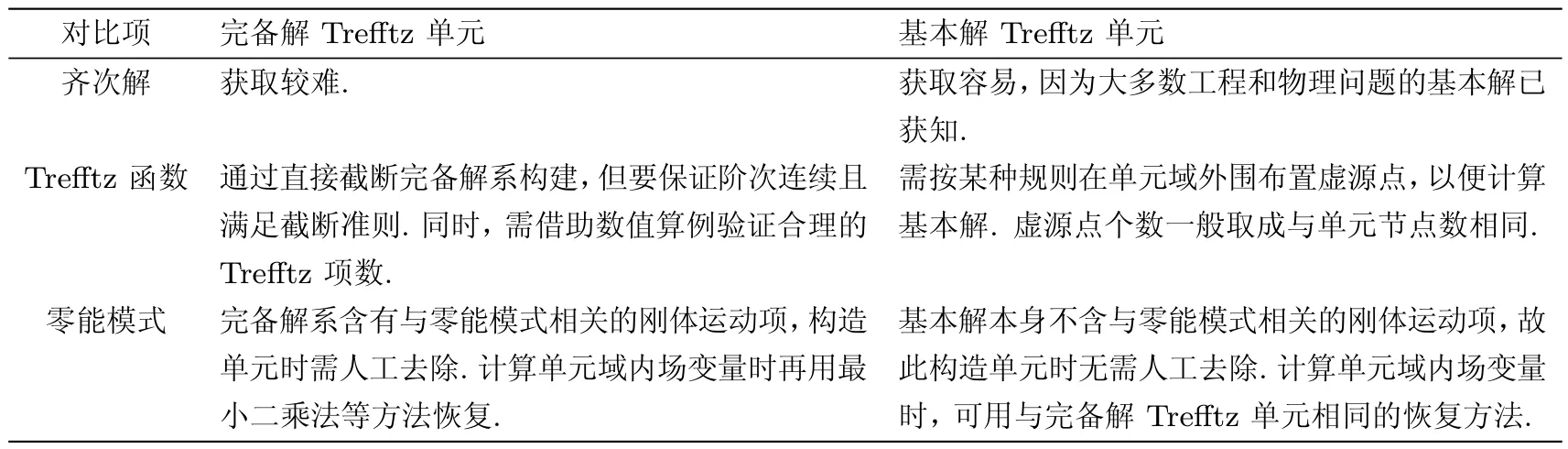
表2 完备解和基本解Trefftz单元情况对比

2 源项的无源化处理

基于前述两个独立的场变量插值模式，结合杂交泛函可推得Trefftz单元刚度方程.对于无源项的工程和物理问题，其控制方程是齐次的，在单元刚度方程推导过程中，采用高斯散度定理可直接消除杂交泛函涉及的域积分[2,12].然而，若源项(如弹性问题中的体力或位势问题中的源汇等)存在，问题的控制方程是非齐次的，高斯散度定理虽仍可消除泛函中的原有域积分，但源项还会衍生另一个新的域积分并出现在单元节点载荷列阵中[2,3335].以各向同性平面位势问题为例，其控制方程为Poisson方程，这里考虑第一类和第二类边界条件，则与该问题等价的杂交泛函Πe为

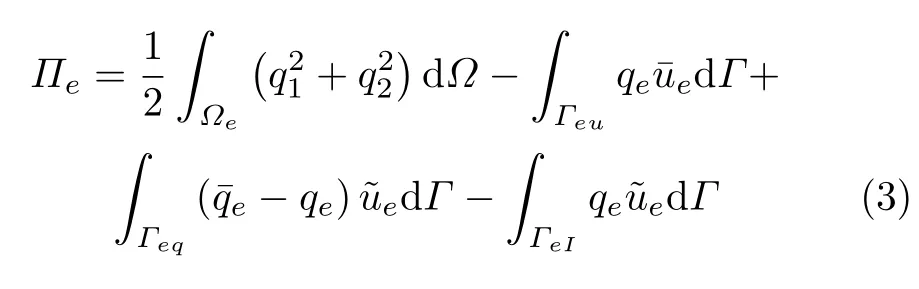
式中，q1和 q2为沿 x,y坐标方向的势流，Γeu和Γeq分别为给定位势e和法向势流e的边界，ΓeI为单元交边界，且有Γe=Γeu∪Γeq∪ΓeI，变量上方的横线表示给定值.应用高斯散度定理，式(3)可改写为

对比式 (4)与式 (3)可以看出，上述操作消去了原泛函右边第一项的域积分 (式 (3)右侧第 1项)，但出现了与源项 b相关的新域积分 (式 (4)右侧第 2项).此时，单元域内插值函数Nej不再满足原问题的控制方程，须增加源项b诱发的特解部分e.众所周知，在传统有限元法中，由于单元列式中含有域积分，因此单元形状受雅可比矩阵控制，相邻单元边内角不能接近或等于180◦，即单元不能过分扭曲，否则会导致计算结果失真甚至无法获得解答.为避免出现传统有限元法面临的尴尬境地，也为保持Trefftz有限元法仅含边界积分的独特优势，研究者们提出了一些处理非齐次方程的方法，但共同作法是将非齐次问题转化为齐次问题求解.目前，主要有格林函数法和径向基函数法. 格林函数法解决了带常体力的平面弹性问题[2].为了处理任意形式的非齐次项情形，Qin[2]和 Wang等[33]基于双重互易边界元法的概念提出了径向基函数法，将径向基函数定义为欧几里得距离的变量，来近似表示源项的函数分布.然后对控制方程求解析积分直接获得相关特解，这样原问题的求解过程就归为寻求特解和齐次解的问题.基于这种求解策略，Weiber等[8,19,28,3637]分析了一系列 Poisson类方程的问题.王克用等[3839]通过坐标变换和径向基函数分析了有源项正交各向异性平面和轴对称位势问题.Moldovan[40]构造了Trefftz应力元并分析了非齐次双曲边值问题.尽管径向基函数在处理非齐次问题时非常便捷，但它可能会造成病态的系数矩阵[41]，不过采取适当的规则化措施[42]避免解答严重失真.

3 特殊功能单元

Trefftz有限元法最大的亮点之一是特殊功能单元.借助这种单元无需局部网格细分，只需在域内插值函数上作调整，就能捕捉各种奇异性或局部效应(如不连续载荷、角点、裂纹、夹杂和孔洞等)，凸显出传统有限元法望尘莫及的效率和优势[2,3132].如前所述，杂交Trefftz单元的域内插值函数精确满足问题的控制方程.若域内插值函数还满足奇异或局部效应区域的边界条件，则可构造相应的特殊功能单元.在现有文献中，研究载荷奇异性的特殊功能单元的文章较少，较早的工作是由Jirousek等[43]完成的，他们推得平面应力状态下的特解构造了集中载荷单元和分布载荷单元.近期，Wang等[44]针对不连续载荷引起的局部效应构造了三种特殊功能单元，分别用于分析弹性体上的点载荷、线载荷和面载荷(图2)，均是基于适当的局部基本解建立的.

在工程实际中，许多结构含有各种各样的孔洞，如螺孔、工艺孔等. 较早研究孔洞单元的是Piltner[45]，他利用复变 Laurent级数推导了椭圆孔单元，该单元能退化为圆孔和内裂纹单元，属于Trefftz型特殊功能单元的范畴，但当时Piltner并没有提出Trefftz有限元的概念.在Piltner[45]工作基础上，王克用[34]引入旋转映射函数构造了可任意调整椭圆孔倾角的特殊功能单元，并应用于接触问题分析中.Leconte等[46]探讨了8节点圆孔单元由线弹性问题推广至非线性问题(冲击)的可能性.Wang等[47]分析了平面弹性问题，以格林函数作为域内插值函数构造了圆孔单元.

学习压力是所有青少年都会面对的压力之一，也是青少年之间最为普遍存在的压力。无论是父母和亲友的期待，还是学生本身对自己学习上的要求，在所有学习阶段对学生产生着极大影响。很多父母都为孩子设计了严格的人生路线，要求孩子必须始终遵从，很多青少年都会面对学习的收获与自身期待不符的问题。这样的情况十分不利于青少年的心理成长，一些年轻人虽然仍然会取得较好的成绩，但无论是生活态度还是学习态度都在学习压力下变得很差。同时，由于社会价值观的功利化，在小学和中学都过于强调分数对学生的影响，无论是在教学上还是在日常生活中。

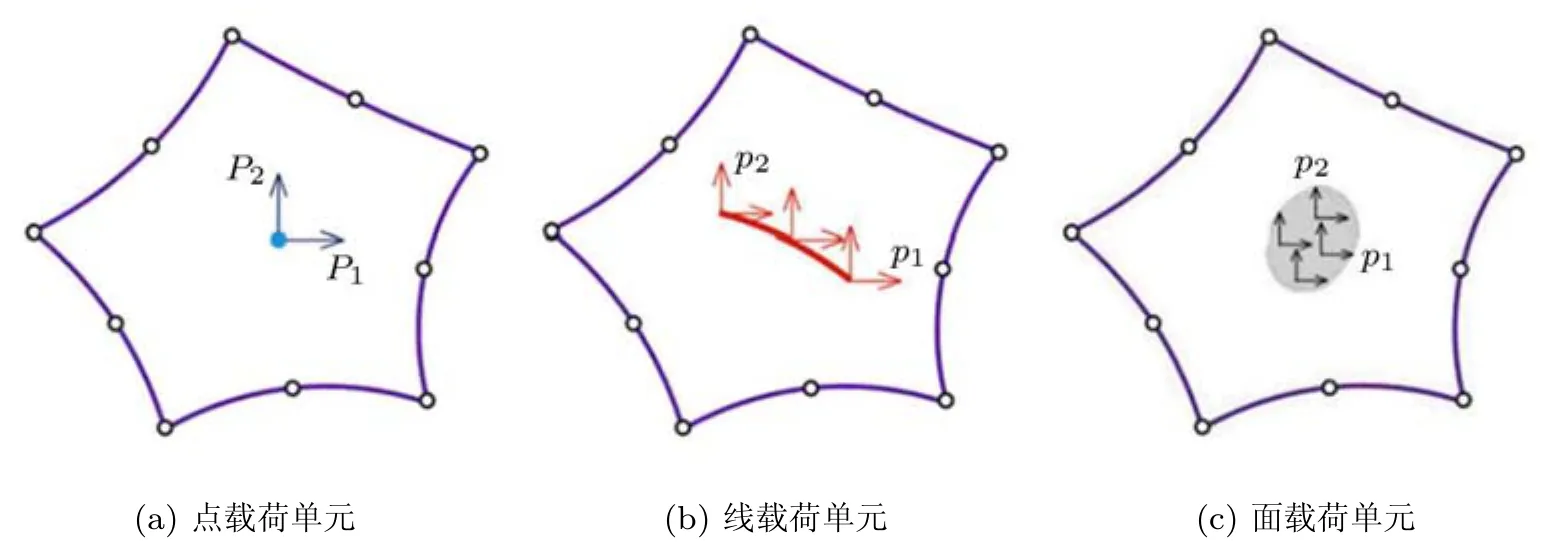
图2 不连续载荷特殊功能单元

若孔洞内填塞有与其形状相同、力学性质不同的材料就形成了夹杂，夹杂与基体之间存在相互作用，如颗粒/纤维增强复合材料等非均质材料.对于这种情形的Trefftz有限元建模与分析，始于Zhang等[4850]的工作.他们先后提出了含图形或椭圆形弹性夹杂/刚性夹杂单元，其构造原理是将原单元分解为两个边值子问题，进而建立单元节点力与位移的关系 (图 3).观察发现，Zhang等[4850]的工作与Voronoi单胞有限元法十分相似，而这种有限元法已经成为模拟非均质材料微观力学特性的强有力工具.张洪武等[51]基于参数变分原理构造了含夹杂Voronoi单元，分析了非均质材料中夹杂对其宏观等效弹塑性力学性能的影响.近期，Dong等[52]在Voronoi单胞有限元理论[53]基础上，提出了Trefftz型Voronoi单胞有限元法，通过引入单元的特征长度，可以有效处理病态方程情形.在单元域内和边界上，借助特征长度这个参数可将Trefftz完备函数限定在[0,1]区间内，这样能确保系统方程组处于良态，无需额外的规则化技术进行处理就能轻松求解.实际上，单元特征长度所起的作用与杂交Trefftz有限元法中通常采用的局部坐标系(o,x,y)[2,12,38-39,43]类同 (图 1).之后，Dong等[14]将其工作推广至含椭圆孔洞以及弹性/刚性夹杂单元.紧接着，Dong等[1516]还构造了三维 Trefftz多边形单元研究球形和椭球形孔洞、夹杂的非均质材料.Wang等[54]则构造了特殊多边形Voronoi纤维/基体单元，用于分析天然大麻纤维复合材料的热效应.从构造原理来看，孔洞单元可视为同形状夹杂单元的特殊情形.此外，Cao等[55]利用适当的局部基本解研究了含缺陷的平面压电问题，Wang等[5657]研究了平面弹性问题的特殊功能单元.关于基于基本解的Trefftz特殊功能单元的综述可参见文献[58].

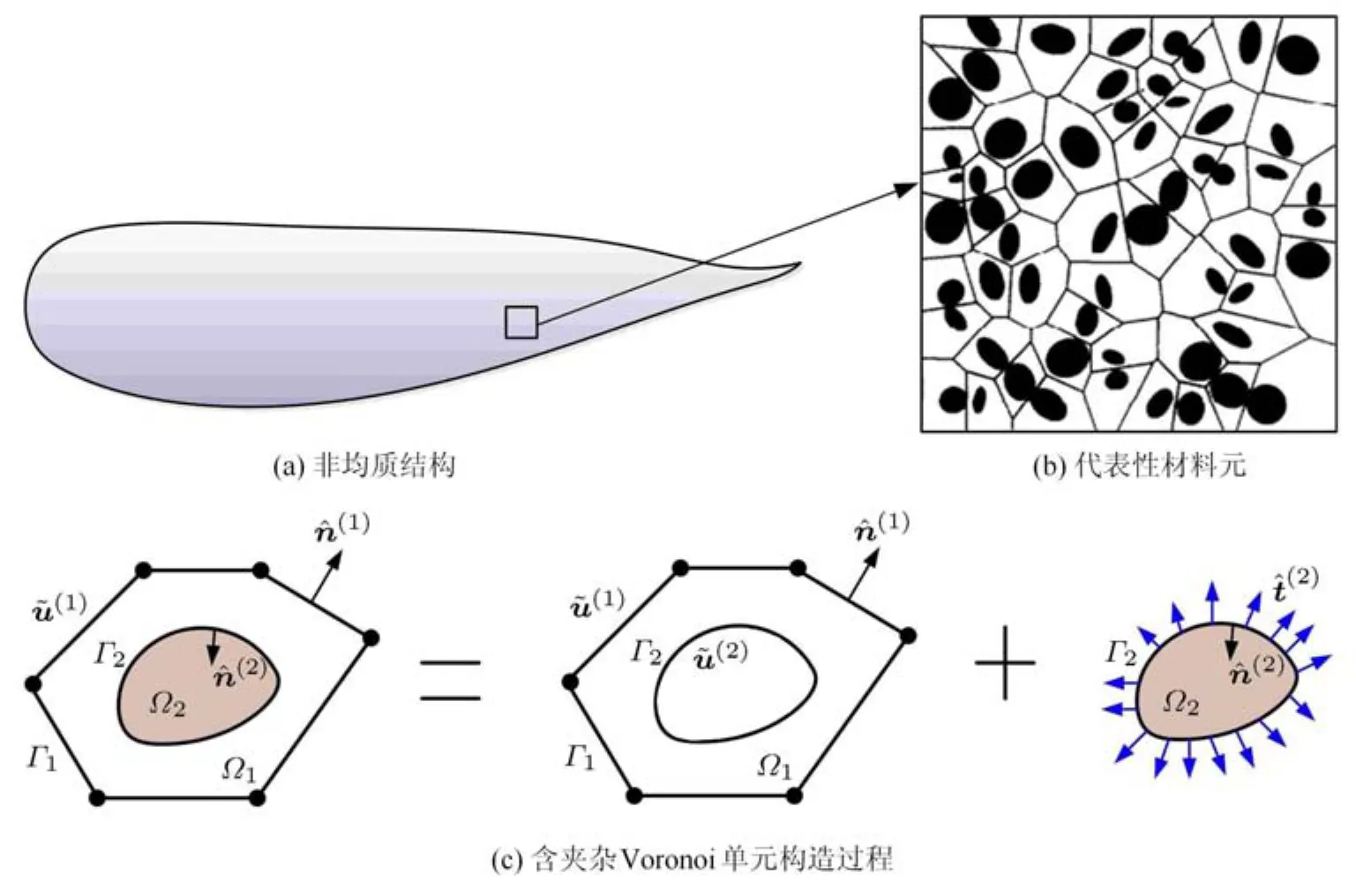
图3 非均质结构与Voronoi单元

此外，Bishay等[59]构造了一系列用于分析带有缺陷、孔洞以及弹性电介质/压电夹杂的压电材料单元.每种单元的外边界条件应用变分原理、配点法或最小二乘法强制满足，而孔洞/夹杂外围应力/电荷自由边界条件则采用配点法/最小二乘法或者特殊解系得到满足.Hennuyer等[60]构造了一种杂交Trefftz超单元，用于模拟航天器结构在碰撞和冲击载荷作用下铆钉装配体的应力集中情况.为了考虑孔边带有初裂纹情形，他们增加了超单元的节点数，尽管改进后的高阶超单元精度有所降低，但仍能对力场进行良好的描绘.Kunter等[61]基于既满足控制方程又满足裂纹边界条件的精确解，构造了Trefftz裂纹单元，且推导了一个含有Dugdale条状屈服区域的二维直裂纹的特解.Chen等[62]基于Hellinger--Reissner变分原理提出了一种多边形角点单元，它虽然可分析含有相互作用的双菱形、双正方形和双矩形孔洞的平面弹性问题，但其只是利用两个角点单元拼接成孔洞而已.这种单元能够较好地捕捉角点奇异性，其精度基本不受角点单元尺寸的影响.

4 非各向同性材料

一些天然或人造材料具有热传导系数等物性参数随方向而改变的特性，包括横观各向同性、正交各向异性和各向异性.鉴于此，研究者们将目光开始转向非各向同性材料的Trefftz有限元法研究，获取非各向同性问题的Trefftz函数成为关键一步.目前主要有直接法和间接法等方法，其中间接法又包括坐标变换法和函数变换法.Wang等[29]利用奇异基本解分析了正交各向异性平面弹性问题.Bussamra等[63]利用 Papkovitch-Neuber位移基构造了三维层合板Trefftz应力元，这种单元非常适合p型自适应性和平行计算.Cao等[64]利用格林函数推得了各向异性弹性介质的基本解，构造了基本解Trefftz层合板单元，并用于分析正交各向异性纤维增强复合材料的力学行为.基于杂交Trefftz泛函，Karkon[65]构造了三角形层合板单元 (THT-7)和四边形层合板单元(QHT-11),分析了各向异性对称的层合板问题.随后，Karkon等[66]又利用 THT-7和 QHT-11单元研究了正交各向异性厚板弯曲问题.赵新娟等[67]利用基本解分析了各向异性平面位势问题.Wang等[68]对位移场变量ui进行函数变换

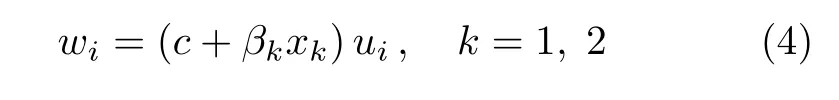
导得平面弹性功能梯度材料的基本解，进而构造出梯度单元.其中，c和βk分别为材料常数和梯度参数.Fu等[9,37]利用Kirchho ff变换

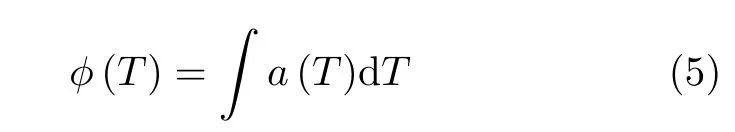
将以温度T为场变量的非线性热传导问题转化为新变量φ的常系数线性问题，进而推得原问题的完备解，分析了材料导热系数随温度按幂律和指数变化的情形.王克用及其合作者[10,12,38]利用简单的坐标变换关系

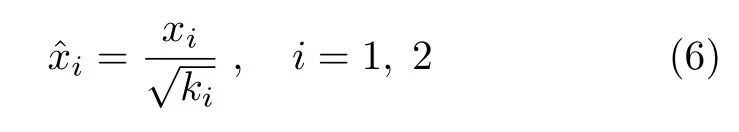
得到正交各向异性平面和轴对称位势问题的完备解，其中ki为沿某一坐标轴的材料特性系数.

此外，Petrolito[69]提出一种杂交Trefftz变分原理[70]，构造了3节点三角形厚板单元，进行了正交各向异性板的振动和稳定性计算.他指出，有限元列式涉及3个刚体模式和1个零能模式，但该零能模式可通过多单元网格划分自动消除.Petrolito还强调，基于杂交Trefftz变分原理[70]构造的单元可自动通过分片试验，进而确保数值解收敛.然而，其有限元列式中含有域积分，本质上并不具备Trefftz单元的优异品质.

5 展望

Trefftz型有限元法发展到今天，在诸多应用领域取得了重要的研究进展，它真正体现了传统有限元法与边界元法思想的完美融合.在下一阶段的研究中，将会在以下几方面受到更多关注：

(1)基本解单元.伴随着传统边界元法的发展，大多数工程和物理问题的基本解已获知，从而可克服寻求完备解系的困难.

(2)特殊功能单元.这类单元不以网格细化为代价即可有效捕捉局部效应，可显著减少建模工作量和机时，将更受工程界的青睐.

(3)源项处理的新方法.源项的无源化处理可消除单元刚度方程涉及的域积分，从而保持Trefftz有限元法对网格畸变不敏感的独特优势.

(4)网格自动划分技术.各种新型(颗粒或纤维增强)复合材料的不断涌现，促进了Trefftz夹杂单元的发展，但相应的多边形网格划分技术尚需完善.

(5)多尺度多物理场耦合分析.Trefftz有限元法在数值计算方面的优异特性使得多物理场模拟成为可能.另外，跨越从米到微米甚至纳米量级的多尺度分析也将是Trefftz有限元法未来的发展趋向.

(6)丰富完善的源程序代码.作为一种高效数值计算方法，Trefftz有限元理论唯经程序化才能真正体现其应用价值.

1 Jirousek J,Leon N.A powerful finite element for plate bending.Computer Methods in Applied Mechanics and Engineering,1977,12(1):77-96

2 Qin QH.The Trefftz Finite and Boundary Element Method.Southampton:WIT Press,2000

3 Qin QH,Wang H.MATLAB and C Programming for Trefftz Finite Element Methods.Boca Raton:CRC Press,2008

4徐鹏,金吾根,万远富.流形 Trefftz直接法.计算力学学报,2008,25(2):260-264

5 Li ZC,Lu TT,Hu HY,et al.Trefftz and Collocation Methods.Southampton:WIT Press,2008

6 Kolodziej JA,Zielinski AP.Boundary Collocation Techniques and Their Application in Engineering.Southampton:WIT Press,2009

7司马玉洲,朱宏平,苗雨.双重互易杂交边界点方法在势问题中的应用.力学与实践,2007,29(6):37-40

8 Weißer S.Arbitrary order Trefftz-like basis functions on polygonal meshes and realization in BEM-based FEM.Computersamp;Mathematics with Applications,2014,67(7):1390-1406

9 Wang H,Han MY,Yuan F,et al.Fundamental-solutionbased hybrid element model for nonlinear heat conduction problems with temperature-dependent material properties.Mathematical Problems in Engineering,2013,2013(3):831-842

10 王克用，李培超，张敏良.正交各向异性位势问题的Trefftz有限元法.力学季刊,2012,33(3):499-506

11 Choo YS,Choi N,Lee BC.A new hybrid-Trefftz triangular and quadrilateral plate elements.Applied Mathematical Modelling,2010,1(1):14-23

12 Wang KY,Zhang LQ,Li PC.A four-node hybrid-Trefftz annular element for analysis of axisymmetric potential problems.Finite Elements in Analysisamp;Design,2012,60:49-56

13 Wang H,Qin QH,Liang XP.Solving the nonlinear Poisson-type problems with F-Trefftz hybrid finite element model. Engineering Analysis with Boundary Elements,2012,36(1):39-46

14 Dong L,Atluri SN.T-Trefftz Voronoi cell finite elements with elastic/rigid inclusions or voids for micromechanical analysis of composite and porous materials. Computer Modeling in Engineeringamp;Sciences,2012,83:183-219

15 Dong L,Atluri SN.Development of 3D T-Trefftz Voronoi cell finite elements with/without spherical voids and/or elastic/rigid inclusions for micromechanical modeling of heterogeneous materials.CMC-Computers Materials and Continua,2012,29:169-211

16 Dong L,Atluri SN.Development of 3D Trefftz Voronoi cells with ellipsoidal voids and/or elastic/rigid inclusions for micromechanical modeling of heterogeneous materials.CMC-Computers Materials and Continua,2012,30:39-81

17 秦庆华.Hybrid-Trefftz有限元简介和展望.力学与实践,1993,15(3):22-24

18 Silva CM,Castro LMSS.Hybrid-displacement(Trefftz)formulation for softening materials.Computersamp;Structures,2007,85(17-18):1331-1342

19 Zhang ZW,Wang H,Qin QH.Method of fundamental solutions for nonlinear skin bioheat model.Journal of Mechanics in Medicineamp;Biology,2014,14(4):1450060

20 Moldovan ID,Cao TD,Teixeira DFJA.Hybrid-Trefftz finite elements for biphasic elastostatics.Finite Elements in Analysisamp;Design,2013,66(66):68-82

21 Freitas JATD,Toma M.Hybrid-Trefftz stress and displacement elements for axisymmetric incompressible biphasic media.Computer Methods in Applied Mechanicsamp;Engineering,2009,198(30-32):2368-2390

22 Moldovan ID,Freitas JATD.Hybrid-Trefftz displacement and stress elements for bounded poroelasticity problems.Computersamp;Geotechnics,2012,42(3):129-144

23 Herrera I.General variational principles applicable to the hybrid element method.National Academy of Sciences,USA,1977

24 Herrera I.Boundary methods:a criterion for completeness.National Academy of Sciences,USA,1980

25 Herrera I,Ewing RE,Celia MA,et al.Eulerian-Lagrangian localized adjoint method:the theoretical framework.Numerical Methods for Partial Differential Equations,1993,9(4):431-457

26 Herrera I,Sabina FJ.Connectivity as an alternative to boundary integral equations:construction of bases.National Academy of Sciences,USA,1978

27 Rezaiee-Pajand M,Karkon M.Two higher order hybrid-Trefftz elements for thin plate bending analysis.Finite Elements in Analysisamp;Design,2014,85(8):73-86

28 Wang H,Qin QH.Hybrid FEM with fundamental solutions as trial functions for heat conduction simulation.Acta Mechanica Solida Sinica,2009,22(5):487-498

29 Wang H,Qin QH.Fundamental-solution-based finite element model for plane orthotropic elastic bodies.European Journal of Mechanics-A/Solids,2010,29(5):801-809

30 Cao C,Qin QH,Yu A.Hybrid fundamental-solution-based FEM for piezoelectric materials.Computational Mechanics,2012,50(4):3 97-412

31 Wang H,Qin QH.Some problems with the method of fundamental solution using radial basis functions.Acta Mechanica Solida Sinica,2007,20(1):21-29

32 Wang H,Qin QH.Hybrid fundamental solution based finite element method:theory and applications.Advances in Mathematical Physics,2015,2015:1-38

33 Wang H,Qin QH,Arounsavat D.Application of hybrid Trefftz finite element method to nonlinear problems of minimal surface.International Journal for Numerical Methods in Engineering,2007,69(6):1262-1277

34 王克用.一种Trefftz孔洞单元及其在接触问题中的应用.力学季刊,2011,32(3):460-465

35 Wang H,Qin QH.FE approach with Green’s function as internal trial function for simulating bioheat transfer in the human eye.Archives of Mechanics,2010,62(6):493-510

36 Cao LL,Wang H,Qin QH.Fundamental solution based graded element model for steady-state heat transfer in FGM.Acta Mechanica Solida Sinica,2012,25(4):377-392

37 Fu ZJ,Qin QH,Chen W.Hybrid-Trefftz finite element method for heat conduction in nonlinear functionally graded materials. Engineering Computations:International Journal for Computer-Aided Engineering and Software,2011,28(5):578-599

38 Wang KY,Li PC,Wang DZ.Trefftz-type FEM for solving orthotropic potential problems.Latin American Journal of Solidsamp;Structures,2014,11(14):2537-2554

39 刘博,王克用,王明红.轴对称Poisson方程的Trefftz有限元解法.应用数学和力学,2015,36(2):140-148

40 Moldovan ID.A new approach to non-homogeneous hyperbolic boundary value problems using hybrid-Trefftz stress finite elements.Engineering Analysis with Boundary Elements,2016,69:57-71

41 Liu RF,Yeih WC,Kuo SR,et al.Indirect T-Trefftz and F-Trefftz methods for solving boundary value problem of Poisson equation.Journal of the Chinese Institute of Engineers,2006,29(6):989-1006

42 Liu CS.Optimally scaled vector regularization method to solve ill-posed linear problems.Applied Mathematics and Computation,2012,218(21):10602-10616

43 Jirousek J,Venkatesh A．Hybrid Trefftz plane elasticity elements with p-method capabilities.International Journal for Numerical Methods in Engineering,1992,35(7):1443-1472

44 Wang H,Qin QH.Numerical implementation of local effects due to two-dimensional discontinuous loads using special elements based on boundary integrals.Engineering Analysis with Boundary Elements,2012,36(12):1733-1745

45 Piltner P.Special finite elements with holes and internal cracks.International Journal for Numerical Methods in Engineering,1985,21(8):1471-1485

46 Leconte N,Langrand B,Markiewicz E.On some features of a plate hybrid-Trefftz displacement element containing a hole.Finite Elements in Analysisamp;Design,2010,46(10):819-828

47 Wang H,Qin QH.Fundamental-solution-based hybrid FEM for plane elasticity with special elements.Computational Mechanics,2011,48(5):515-528

48 Zhang J.A hybrid finite element method for heterogeneous materials with randomly dispersed rigid inclusions.International Journal for Numerical Methods in Engineering,1995,38(10):1635-1653

49 Zhang J,Katsube N.A hybrid finite element method for heterogeneous materials with randomly dispersed elastic inclusions.Finite Elements in Analysisamp;Design,1995,19(1):45-55

50 Zhang J,Katsube N.A polygonal element approach to random heterogeneous media with rigid ellipses or elliptical voids.Computer Methods in Applied Mechanicsamp;Engineering,1997,148(3-4):225-234

51 张洪武,王辉.基于参数变分原理的含夹杂 Voronoi单元法及非均质材料弹塑性计算.复合材料学报,2007,24(4):145-153

52 Dong L,Atluri SN.Development of T-Trefftz four-node quadrilateral and Voronoi cell finite elements for macro-amp;micromechanical modeling of solids.CMES:Computer Modeling in Engineeringamp;Sciences,2011,81(1):69-118

53 Ghosh S,Mallett RL.Voronoi cell finite element.Computersamp;Structures,1994,50(1):33-46

54 Wang H,Qin QH,Xiao Y.Special n-sided Voronoi fiber/matrix elements for clustering thermal effect in natural-hemp- fi ber- fi lled cement composites.International Journal of Heatamp;Mass Transfer,2016,92:228-235

55 Cao C,Yu A,Qin QH.A new hybrid finite element approach for plane piezoelectricity with defects.Acta Mechanica,2013,224(1):41-61

56 Wang H,Qin QH.Fundamental-solution-based hybrid FEM for plane elasticity with special elements.Computational Mechanics,2011,48(5):515-528

57 Qin QH,Wang H.Special circular hole elements for thermal analysis in cellular solids with multiple circular holes.International Journal of Computational Methods,2013,10(4):683-728

58 王辉,赵新娟,白杨等.基于基本解的杂交有限元法及特殊孔洞单元的构造理论.第十四届北方七省市区力学学会学术会议,中国威海,2012

59 Bishay PL,Atluri SN.Trefftz-Lekhnitskii Grains(TLGs)for efficient direct numerical simulation(DNS)of the micro/meso mechanics of porous piezoelectric materials.Computational Materials Science,2014,83(2):235-249

60 Hennuyer C,Leconte N,Langrand B,et al.Interpolation functions of a hybrid-Trefftz perforated super-element featuring nodes on the hole boundary.Finite Elements in Analysisamp;Design,2014,91(91):40-47

61 Kunter K,Heubrandtner T,Suhr B,et al. A hybrid crack tip element containing a strip-yield crack-tip plasticity model.Engineering Fracture Mechanics,2014,129:3-13

62 Chen MC,Ping XC,Liu WH,et al.A novel hybrid finite element analysis of two polygonal holes in an in finite elastic plate.Engineering Fracture Mechanics,2012,83:26-39

63 Bussamra FLS,Neto EL,Jr DSR.Hybrid quasi-Trefftz 3D finite elements for laminated composite plates.Computersamp;Structures,2012,s92-93(3):185-192

64 Cao C,Yu A,Qin QH.A novel hybrid finite element model for modeling anisotropic composites.Finite Elements in Analysisamp;Design,2013,64(2):36-47

65 Karkon M.Hybrid-Trefftz formulation for analysis of anisotropic and symmetric laminated plates.Composite Structures,2015,134:460-474

66 Karkon M,Rezaiee-Pajand M.Hybrid-Trefftz formulation for analysis of thick orthotropic plates.Aerospace Scienceamp;Technology,2016,50:234-244

67 赵新娟,赵吉义.位势问题的杂交有限元算法研究.中原工学院学报,2011,22(1):59-61

68 Wang H,Qin QH.Boundary integral based graded element for elastic analysis of 2D functionally graded plates.European Journal of Mechanics-A/Solids,2012,33(3):12-23

69 Petrolito J.Vibration and stability analysis of thick orthotropic plates using hybrid-Trefftz elements. Applied Mathematical Modelling,2014,38(24):5858-5869

70 Petrolito J.Vibration and stability of plates using hybrid-Trefftz elements.International Journal of Structural Stabilityamp;Dynamics,2011,4(4):559-578

RESEARCH ADVANCES IN THE TREFFTZ FINITE ELEMENT METHOD

WANG Keyong1)LI Peichao
(School of Mechanical Engineering,Shanghai University of Engineering Science,Shanghai 201620,China)

The Trefftz finite element method(TFEM)is an efficient numerical approach with many joint advantages of the conventinal finite and boundary element methods.Based on the mutual independent interpolation modes,the finite element formulation involving the boundary integrations only is derived by incorporating the hybrid functional and the Gaussian divergence theorem.The research advances in the internal interpolation function,the treatment of the source term,the special-purpose element and the nonisotropic material during the past decade(2007-2016)are reviewed and several directions are pointed out for the future development.

Trefftz finite element method,internal interpolation function,boundary integration,specialpurpose element,non-source treatment

O343.1

A

10.6052/1000-0879-17-115

2017-04-05收到第1稿，2017-05-03收到修改稿.

1)王克用，博士，副教授，主要研究方向为Trefftz有限元法和多孔介质传热.E-mail:k.y.wang@126.com

王克用,李培超.Trefftz有限元法的研究进展.力学与实践,2017,39(5):433-440

Wang Keyong,Li Peichao.Research advances in the Trefftz finite element method.Mechanics in Engineering,2017,39(5):433-440

(责任编辑:胡 漫)