小天体平衡点之谜1)

姜 宇 李俊峰 (西安卫星测控中心宇航动力学国家重点实验室，西安710043)(清华大学航天航空学院，北京100084)

小天体平衡点之谜1)

姜 宇∗,2)李俊峰†,3)∗(西安卫星测控中心宇航动力学国家重点实验室，西安710043)†(清华大学航天航空学院，北京100084)

为了解释小天体平衡点个数的内在规律，介绍了小天体引力场中平衡点的一个守恒量，解释了小天体非退化平衡点个数是奇数的原因.通过若干个有代表性的小天体的形状和相对旋转坐标系的有效势能在赤道面内投影,形象生动地介绍了具体的小天体平衡点的个数情况.给出了观测到的小天体基本都有奇数个平衡点的数学解释.

小天体，平衡点，引力势

平衡点[12]是力学中的一个基本的概念，对于一个物体的运动来说，当它处在平衡点位置的时候，所受的合外力是零，但未必是稳定的.例如一个小球处在光滑碗的碗底和碗沿上，合外力都为零，碗底和碗沿都是这个小球运动的平衡点.对于这个小球来说，碗沿上的每一个点都是它的平衡点，碗底也是它的一个平衡点，因而光滑碗中的小球运动有无穷多个平衡点.

1 大行星的平衡点

在太空中，也存在着类似的平衡点[1]，比如地球静止轨道上的卫星，相对于地球表面来说是静止不动的，这样的卫星就处在地球引力场中的相对平衡点上，虽然在惯性空间来看，地球和地球静止轨道上的卫星都是运动的，但它们之间却是相对静止的.火星等其他大行星也有静止轨道.不失一般性，以火星为例，火星静止轨道上的卫星相对于火星表面来说是静止不动的，火星静止轨道上的点就是火星的相对平衡点.大行星由于质量较大，引力足以克服固体应力，使大行星达到流体静力学平衡，因此大行星都近似为球形.大行星的平衡点包括其静止轨道上所有点，以及大行星的质心.

地球上有山脉和河流，地球赤道半径和两极半径有所不同.其他大行星如火星表面有峡谷、火山与陨石坑，木星等气态行星的外形为两极扁而赤道鼓.如果考虑大行星的精确的引力场，严格地来说，大行星静止轨道上只有4个点是平衡点.因此，大行星的平衡点实际上共有5个.

此外，太阳--木星系统中存在特洛伊小行星，这些小行星所处的位置是日--木系统的平衡点，这样的平衡点相对于太阳和木星连线是静止不动的.

2 小天体的平衡点

太阳系中，目前已经发现并获得永久编号的小天体有几十万个，这些小天体质量较小，自身引力不足以克服固体应力，不能达到流体静力学平衡，具有不规则的几何外形.通常来说，绝大多数小天体都是匀速自旋的.在这些匀速自旋的小天体的引力场中，也存在着相对平衡点[35].本文所述的小天体都是指匀速自旋的.一个天体的平衡点是其有效势的临界点，也就是有效势的导数等于零的点.有效势在数值上等于引力势能和旋转势能之和.以小行星6489 Golevka为例，我们来看引力势能和旋转势能是如何组合成有效势的，取小天体固连坐标系，原点为小天体质心.图1给出了小行星6489 Golevka赤道面的引力势能的影像图和立体图，图2给出了该小行星的旋转势能的相应图像.从图1和图2的立体图可见，引力势能和旋转势能的开口方向相反.引力势能的立体图像一座山，且越远的地方海拔越接近零.而旋转势能的立体图则像一个边缘无穷延伸的一只大碗一样，越远的地方数值越大，中心位置处的数值最小.图3给出了小行星6489 Golevka赤道面的有效势的影像图和立体图.有效势作为引力势能和旋转势能之和，从图1∼图3可见，有效势大致的开口方向和旋转势能的开口方向相同，但引力势能和旋转势能相加后使得中心附近有一定凸起，就像一个盆地中央有一座小山一样.

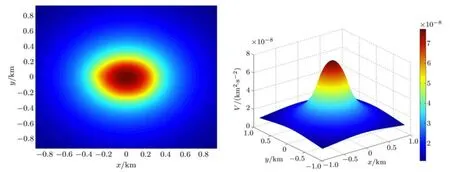
图1 小行星6489 Golevka赤道面的引力势能的影像图和立体图

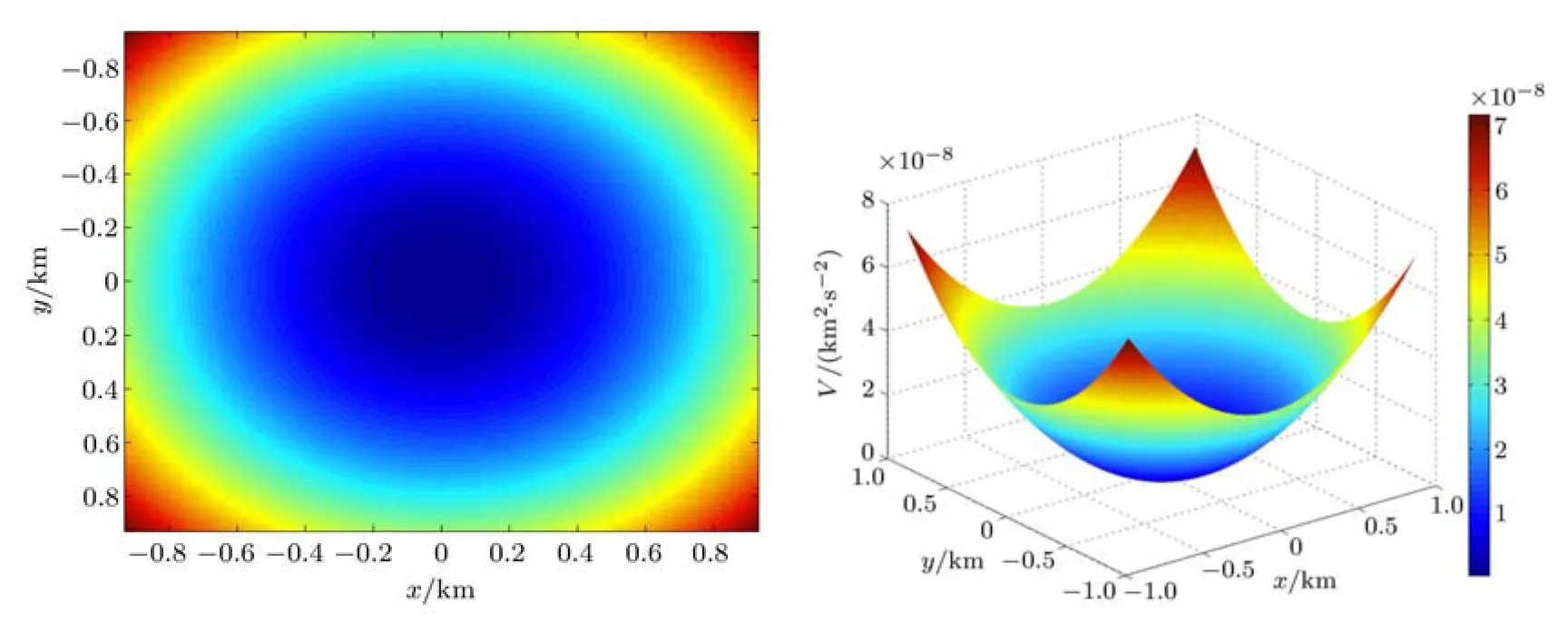
图2 小行星6489 Golevka赤道面的旋转势能的影像图和立体图

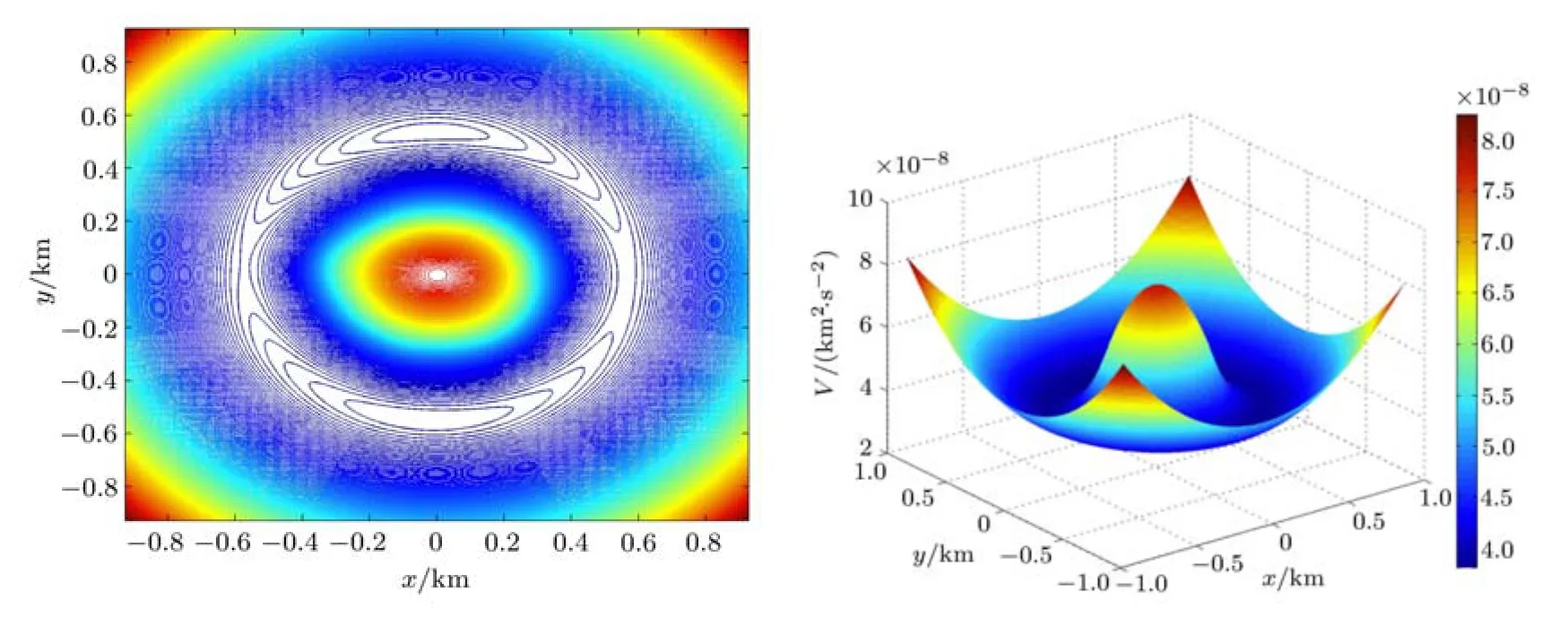
图3 小行星6489 Golevka赤道面的有效势的影像图和立体图

我们可以换个角度来理解引力势能和旋转势能的相加成为有效势.做一个“填坑游戏”.已经画出了旋转势能的立体图，旋转势能的立体图像一个无限延伸的碗一样，在旋转势能上加引力势能就相当于在碗的中心填一铲子土.原来的大碗只有一个平衡点，就在碗底的中央，是碗的最低点.而加上一铲子土以后，原来的唯一的平衡点依然是平衡点，只不过从最低点(最小值点)变成了局部极大值点，同时在局部极大点周围产生了若干个其他平衡点.

也可以从旋转势能和引力势能的梯度来理解平衡点.如果记V(r)=W(r)+U(r)为有效势，其中W(r)为旋转势能，U(r)为引力势能，为小天体引力场中的位置矢量.平衡点就是满足▽V(r)=0的点，也就是 ▽W(r)=−▽U(r)的点.因此平衡点就是满足旋转势能的梯度和引力势能的梯度大小相等、方向相反的点，换句话说，平衡点就是旋转势能的梯度和引力势能的梯度势均力敌的点.事实上，旋转势能的梯度大小就等于离心力，引力势能的梯度的大小就等于万有引力.平衡点就是引力与离心力相等的点.

3 平衡点有几个

由于不同的小天体的自旋速度、形状等各异，所以不同的小天体的平衡点的位置和稳定性不同，就连平衡点的个数也可能不同[2].那么这几十万个小天体的平衡点到底有多少个？有没有什么规律呢？我们可以通过画出小天体旋转坐标系来看的有效势能来了解平衡点的个数.图 4是一些小行星的平衡点和相对旋转坐标系的有效势能在赤道面内投影图，体内的平衡点可以从有效势在赤道面内的投影图中看出.我们可以看到这几个小行星的平衡点个数为9,7,5和1.目前已知的小天体中，有5个平衡点的包括 4 Vesta,243 Ida,433 Eros,951 Gaspra,1620 Geographos,1996 HW1,2063 Bacchus,2867 Steins,4769 Castalia,6489 Golevka,25143 Itokawa,52760，彗核 1P/Halley,9P/Tempel1,103P/Hartley2以及大行星的卫星 J5 Amalthea,M1 Phobos,N8 Proteus,S9 Phoebe,S16 Prometheus.有7个平衡点的包括216 Kleopatra和1580 Betulia.有1个平衡点的包括 1998 KY26和 54509 YORP.有 9个平衡点的包括101955 Bennu[36].

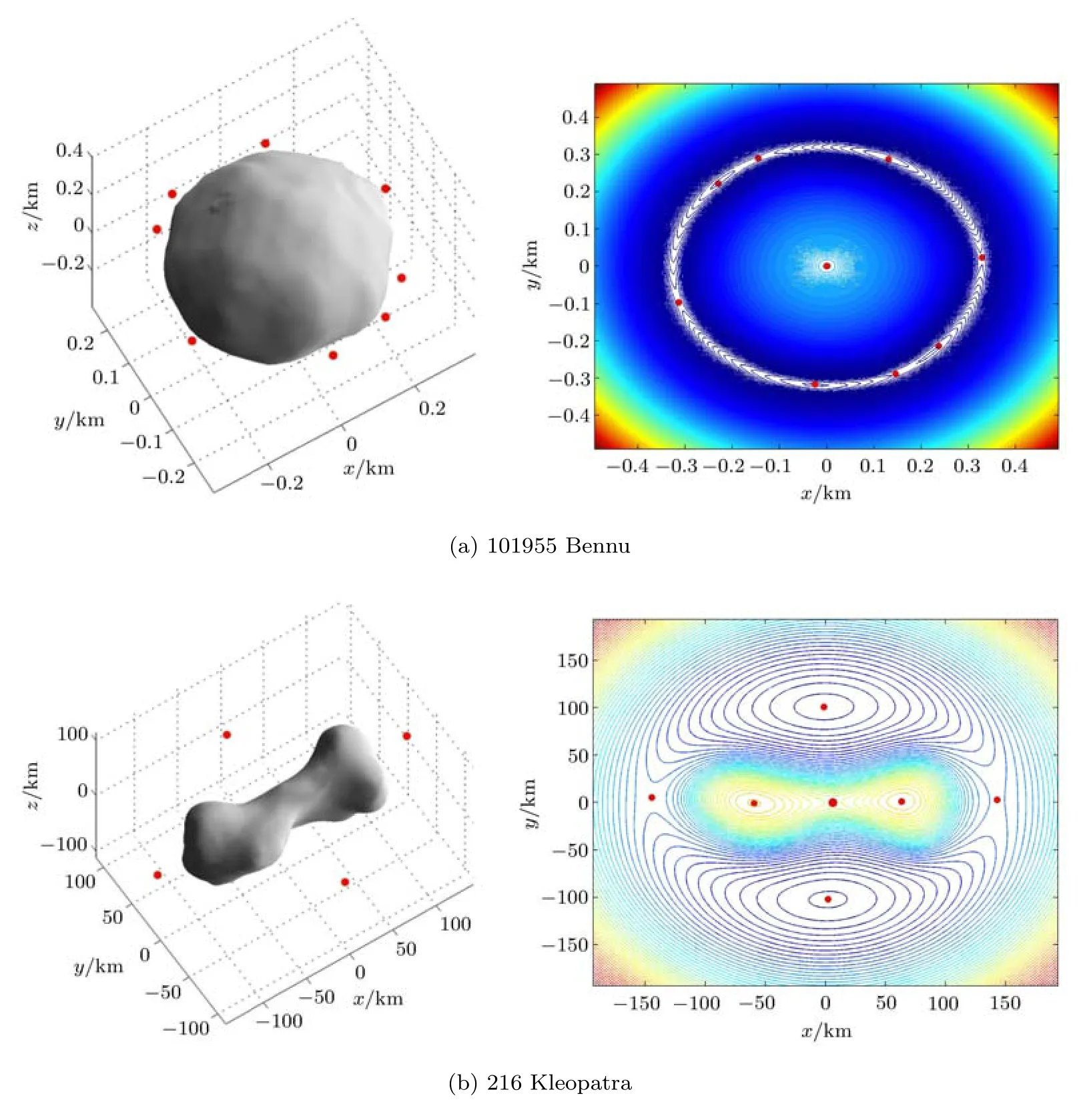
图4 若干小行星的平衡点和相对旋转坐标系的有效势能在赤道面内投影

图4 若干小行星的平衡点和相对旋转坐标系的有效势能在赤道面内投影(续)

图4 若干小行星的平衡点和相对旋转坐标系的有效势能在赤道面内投影(续)

可见，小天体平衡点与大行星平衡点有很大不同.如果认为大行星是球形，那么每个大行星有无穷多个平衡点，包括大行星静止轨道上的所有点和大行星的质心；而小天体平衡点是有限多个，可能是1,5,7,9等.如果考虑大行星的精确引力场，那么每个大行星有5个平衡点，其中1个在大行星的体内质心处；而小天体的平衡点可能是5个，也可能是1个、7个、9个或其他数字，小天体的体内平衡点可能是1个，也可能多于1个.

下面我们首先不想那些高深的数学和浩如烟海的天体力学知识，不受已有的思维方式限制，避免在前人的思维框架下受到束缚.我们心中只是一张白纸，像小孩一样，面对这些问题，好奇心促使我们想象和猜测其中的奥秘.我们发现这些数字都是奇数，那么小天体的平衡点都是奇数个吗？对于平面圆形限制性三体问题来说，有5个平衡点；在平面圆形限制性三体问题的两个大天体之间用一个无质量细直棒来连接，那么这两个大天体就像一个匀速自旋的不规则体一样，在它的引力场中有包括两个大天体质心在内的7个相对平衡点，是奇数.

我们做一个思想实验，想象一个不规则天体的外形、大小和转速等参数发生改变.例如从 101955 Bennu变为1580 Betulia，再变为1620 Geographos，再变为1998 KY26.那么平衡点的个数从9变为7，再变为5，然后再变为1.图5给出了在转速变化下小行星 216 Kleopatra的会发生撞在一起相互 “融合”的平衡点.初始参数下，小行星216 Kleopatra有7个相对平衡点.在小行星转速增大时，平衡点E3和E6首先发生融合，此时总的平衡点的个数变为6，融合后E3和E6这两个平衡点消失，只剩下5个平衡点[5].转速进一步增大，平衡点E1和E5发生融合湮灭，平衡点个数从5变为4再变为3.转速继续增大，平衡点E2和E7发生融合湮灭，最后只剩下1个平衡点E4.

我们分析参数变化下平衡点的个数从一个奇数变为另一个奇数的过程中，首先是两个平衡点接近并瞬间融合为1个平衡点，这融合后的1个平衡点只存在于一瞬间，此后由于参数的继续变化而消失.正如地表的高度有山峰、山谷和马鞍状的山脊，它们都属于平衡点，当我们铲平一个山峰的时候，一定会出现山峰和马鞍状的山脊合二为一的情况；当我们填满一个山谷的时候，一定会出现山谷和马鞍状的山脊合二为一的情况.这种由两个不同的平衡点瞬间融合产生的1个平衡点的特性应当同一般的平衡点不同.

因此我们猜测在参数变化下，小天体引力场中的平衡点个数出现偶数的时候，往往会有1个平衡点是融合产生的，它的特性与其他平衡点不同.那么到底哪方面的特性不同呢？我们知道一个力学系统的平衡点存在若干个特征值，这些特征值决定了平衡点附近局部运动的特性.这里我们回顾特征值的一点知识，继续想象.当两个平衡点逐渐接近时，沿着两个平衡点连线方向的无质量质点的局部运动就会逐渐变为 “动也不是，不动也不是”的神奇状况.倘若质点运动，则运动范围受限，两个平衡点越来越近；倘若质点不运动，也不可能，毕竟两个平衡点的特性有所不同，局部的结构决定了沿着两个平衡点连线方向的质点必须运动.随着两个平衡点越来越接近，这种矛盾会越来越剧烈，最终当两个平衡点无限接近的时候，沿着两个平衡点方向的运动静止了，这就对应着零特征值的出现.因此我们猜测两个没有零特征值的平衡点融合产生了一个有零特征值的平衡点.在数学上，有零特征值的平衡叫做退化平衡点，没有零特征值的平衡叫做非退化平衡点.

图5 在转速变化下会发生相互融合的小行星平衡点，以小行星216 Kleopatra为例

通过上述思想实验，我们猜测：小天体引力场中的非退化平衡点的个数必是奇数.我们尝试寻找合适的数学工具来论证上述猜测是否正确，此时，我们把扔掉的所有的数学知识和天体力学知识一股脑地都捡回来，然后在其中搜索那些可能对于证明我们的猜测是有用的，文献[5]给出了上述猜测的数学证明，证明过程使用了拓扑度理论，对证明过程有兴趣的读者可以进一步阅读.

下面我们给出文献 [5]的核心结论.小天体的每个平衡点都有 6个特征值，如果一个小天体引力场中的平衡点个数为 N，我们把第 i个平衡点记为 Ei，Ei的第 j个特征值记为 λj(Ei)，记指标文献 [5]提出并证明了下面的恒等式

从这个恒等式可以知道每一个平衡点都有一个指标，这个指标的值只能是 −1,0或1.当平衡点有零特征值时，指标为0.有零特征值的平衡点称为退化平衡点.所以对于非退化平衡点来说，它的指标不为0.而且指标为1的平衡点的个数永远比指标为−1的平衡点的个数多1个.如果指标为−1的平衡点的个数为k，那么指标为1的平衡点的个数为k+1个，非退化平衡点的个数则为2k+1.这就说明一个小天体引力场中至少有1个平衡点.所以小天体引力场中非退化平衡点的个数是奇数.对于均质球状的匀速自旋体来说，退化平衡点连接成一个圆，一个例子就是地球静止轨道.

对于一般的不规则天体，文献[5]给出了参数变化下，平衡点个数可以从7个依次变为6,5,4,3,2,1的算例.当平衡点个数为偶数的时候，出现了奇数个退化平衡点，因此非退化平衡点的个数依然是奇数.并且平衡点个数为偶数只发生在参数漫长变化过程中的一瞬间.

因此我们知道，小天体引力场中的平衡点个数可以是奇数，也可以是偶数，甚至可以是无穷多个.小天体引力场中的平衡点的个数最少为1个.最少有1个非退化的平衡点.一个匀速自旋的不规则体引力场中的非退化平衡点个数一定是奇数.此外，对于目前已知的小天体来说，由于小天体都具有不规则的几何外形，且能达到使得平衡点个数为偶数的情况的参数只是参数漫长变化过程中的一瞬间，因此我们观测到的绝大多数小天体的平衡点个数都是奇数个，都没有退化平衡点.本文介绍的结论，对于一切匀速自旋体产生的引力场都成立.

4 结束语

天体力学中关于限制性三体问题的优秀文献汗牛充栋，但却没有文献质疑和解释平衡点个数的奇偶性问题.本文介绍的解决问题思路可以推广到其他的领域，那就是我们在面临一个新事物的时候，可以尝试着抛弃已有的理论、知识、方法和思维定式，像一个婴儿一样看世界，猜测其中可能的奇妙之处.在发现或猜想出可能的规律之后再把原来学过和没学过的理论、知识、方法捡回来，尝试着论证相关发现或猜想.

近年来，人类发射了若干个针对小天体的探测器，开展对太阳系小天体的科学探测.未来我们对小天体的了解越来越多，对于小天体附近的轨道、小天体结构等蕴含的力学问题的认识也将越来越深刻.

1 刘延柱.关于地月系统的拉格朗日点.力学与实践,2015,37(6):765-768

2 陈立群.稳定性漫谈.力学与实践,2015,37(1):148-151

3 Jiang Y,Baoyin HX,Li JF,et al.Orbits and manifolds near the equilibrium points around a rotating asteroid.Astrophysics and Space Science,2014,349(1):83-106

4 Wang XY,Jiang Y,Gong SP.Analysis of the potential field and equilibrium points of irregular-shaped minor celestial bodies.Astrophysics and Space Science,2014,353(1):105-121

5 Jiang Y,Baoyin HX,Li HN.Collision and annihilation of relative equilibrium points around asteroids with a changing parameter.Monthly Notices of the Royal Astronomical Society,2015,452(4):3924-3931

6 Chanut GGT,Winter CO,Amarante A,et al.3D plausible orbital stability close to asteroid(216)Kleopatra.Monthly Notices of the Royal Astronomical Society,2015,452(2):1316-1327

O317

A

10.6052/1000-0879-16-257

2016-08-09收到第1稿，2016-08-13收到修改稿.

1)国家自然科学基金(11572166)和国家重点基础研究发展计划(973)(2012CB720000)资助项目.

2)姜宇，博士，主要研究方向为航天动力学与控制.E-mail：jiangyuxian china@163.com

3)李俊峰，教授，主要研究方向为深空探测器动力学、轨迹设计与控制.E-mail:lijunf@tsinghua.edu.cn

姜宇，李俊峰.小天体平衡点之谜.力学与实践,2017,39(5):509-515

Jiang Yu,Li Junfeng.The mystery of equilibrium points around minor celestial bodies.Mechanics in Engineering,2017,39(5):509-515

(责任编辑:胡 漫)