鸡蛋在水滴上的直立及水中的稳定平衡

2017-11-22尤明庆

力学与实践 2017年5期

关键词：势能浮力曲率

尤明庆

(河南理工大学能源科学与工程学院，河南焦作454010)

鸡蛋在水滴上的直立及水中的稳定平衡

尤明庆1)

(河南理工大学能源科学与工程学院，河南焦作454010)

蛋壳没有显著的接触变形，水洗干燥之后难以在坚硬光洁的平面上直立；但依赖两三颗细小盐粒或者水膜的辅助支承即可实现大端直立.蛋在液体中姿态与浮力有关，可在水中以小端直立.与刚体、浮体相同，潜体在重力、浮力和支承力作用下处于稳定平衡时势能达到极小值.

稳定平衡，表面张力，潜体，浮力，势能

立春或春分竖蛋因电视和网络的推介已不再局限于地方风俗.竖蛋牵涉到刚体以表面一点支承的稳定平衡问题，相关的力学定理是：支承点处法线通过重心且曲率半径大于重心高度[1].显然，鸡蛋对称轴两个端点只是不稳定平衡位置，不过网上有大量竖蛋照片，对此需要做出说明；而水中蛋体具有多种稳定平衡姿态，也需要给出解释.

1 竖蛋

文献[2]称“实际的鸡蛋壳表面并不光滑，粗糙的尖端存在许多突起的小点与桌面接触，这些接触点围成一个很小的区域.鸡蛋的重力只要不越出这个小区域就能直立不倒”，与维基百科 (Wikipedia)所述类似[3].不过，肉眼或在小倍放大镜下看来，鸡蛋外壳通常并无明显突起，而鸭蛋外壳更是坚硬光洁.蛋壳具有一定的刚度，不会产生显著的接触变形以增大支承面积.

鸡蛋大端的气腔因薄膜而大致固定，可以手电或蜡烛等小光源检查；吃蛋时先敲大端颇为合理，而《格列佛游记》中小人国竟就此发生争论乃至战争.气腔使鸡蛋的重心偏离形心而远离大端.笔者觉得，经水洗、干燥后的鸡蛋或鸭蛋，倘若表面光洁，似难以直立在干净玻璃、抛光石材或平整木桌的表面上.不稳定平衡位置的实现并不容易，认为“只要有足够耐心，在任何时刻任何地点都能将鸡蛋竖起来”的人或许没有伸手一试.网上有许多小学生的作文叙述了未能成功的经历.

当然，因地面、木板表面的微小凹坑或桌布柔软变形，鸡蛋能够直立.wikihow介绍的方法“Make a small mound of salt on a hard,smooth,level surface；carefully balance the egg on top of the salt,then gently blow the excess salt away”[4]也确实可行.试验表明，竖直鸡蛋，轻轻前推，受阻即止，尺度不足 0.5mm的两三颗盐粒即可实现鸡蛋的大端直立.作为参考，若鸡蛋大端曲率半径 18mm，0.3mm和0.1mm高度的盐粒支撑，其距鸡蛋顶点分别为 3.3mm和1.9mm；因而稳定直立是容易实现的.又，盐粒尺度较小且硬度较高，可嵌入蛋壳，从而竖蛋可便利地重复进行.不过，如此“作弊”的行为真是需要提醒大家呢.

鸡蛋个体差别很大，部分以大端静立水滴之上两三分钟后即能直立 (图 1)，可抵抗口腔呼气的轻微扰动而稳定 60h.笔者已如此竖立 8个不同鸡蛋，累计12次以上.

图1 鸡蛋的尺寸(mm)及水滴上的直立

当然，并不是所有鸡蛋都能借助水滴而直立，如图1左侧鸡蛋经多轮极度耐心的努力仅获得1s的短暂直立.又，熟鸡蛋因气腔固定或许不再具有轴对称性，似难以直立；但以小端或大端如陀螺旋转即可直立，在平卧状态快速转动后稳定姿态亦可变化为直立，多为大端在下[5].生鸡蛋直立时难以施力使其旋转，平卧时也需多次驱动才能逐步增速，且难以转为直立，而抓起再放回桌面后却可因内部液体的惯性而继续转动.据此可便利地确认鸡蛋之生熟.

图 1右侧所立鸡蛋高 54.3mm,中间直径44.0mm;经拍照测量，大端顶点的曲率半径 R为18mm 或略大，且可确认顶点附近不存在局部平面，难以直接立在抛光的石材表面.不过，石材台面和鸡蛋外壳都是沾水的，表面张力使鸡蛋与桌面接触点周围形成边缘厚度约1mm水垫，内部压力低于大气压，等价于在鸡蛋底部提供拉力而有助于稳定平衡；不过，实际计算表明这并不是决定性因素.

鸡蛋与桌面接触点附近可以用曲率半径R的球面来代替(图2)，水垫厚度h和直径d满足

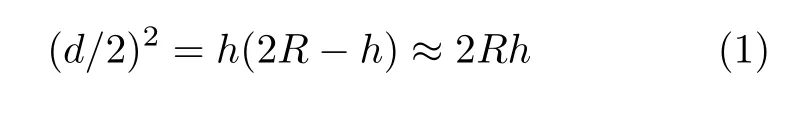
水的表面张力系数TS，水垫内压强低于大气压的数值近似为

图2 鸡蛋与桌面的接触点及水垫

该压差引起鸡蛋底部受到向下的等效拉力为

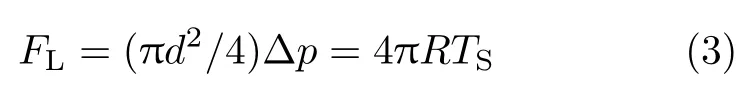
该值与水垫的几何尺度--直径或厚度无关.TS在20◦C时为73mN/m，FL=16.5mN；作为参照，60g鸡蛋的重量是588mN.又，水垫厚度h=1mm时直径d=12mm，相应的压强差近似为146Pa，相当于15mm高水柱的压力.对于图1右侧鸡蛋，重心高度约25mm，底部作用数值为重量3%的拉力不能将合力作用点降低到18mm，即曲率中心的高度,因而单纯的表面张力作用不足以使鸡蛋满足大端直立的稳定平衡条件.

尺度较小时水与固体的关系非常复杂.就所讨论的鸡蛋而言，d=2mm时h=0.028mm，若考虑到鸡蛋顶端的微小接触变形，其与桌面之间存在一个直径2mm、间隙小于0.02mm的区域，固体的引力以及自身黏性使得水不易流动，类似于结合水而传递压力，具有支承能力.

水的辅助支承主要在接触点附近的微小区域，因而水滴竖蛋也不是伸手可得的事情；不过，鸡蛋只要能够直立，水垫蒸发而近乎消失时也能维持稳定--即使不考虑蛋壳粗糙，其下方至少有直径1mm的区域充水厚度小于0.005mm.该尺度是百元纸币厚度0.1mm的1/20，与黏粒上限相当；而干硬黏土的强度来源于包裹黏粒的结合水.

值得一说的是，乡村孩童头疼发烧时(多为病毒性感冒)，家长或请他人将洗净的鸡蛋立在碗中“叫魂”而后让小孩食用.碗底微凹减小了缝隙的厚度(图2)，增加了水滴支承的范围和强度，直立鸡蛋的困难显著减小；而病毒性感冒属于自限性疾病，在物理降温后进行精神安慰并补充营养，才是适当的处置方法.

2 水中的蛋

基于浮力定律，利用台秤测得新鲜鸡蛋的比重在1.07g/cm3左右.鸡蛋在水中不能浮起，其重心与浮心都在对称轴上，但并不重合；因大端存在气室浮心比重心更靠近大端.若以大端支承，鸡蛋稍偏离竖直位置，因重心在上，且重力大于浮力，必然继续偏离而失稳.这很容易得到试验确认.

蛋以小端支承，浮心B在上、重心W 在下，均高于小端顶点处曲率中心C∗.记浮心、重心至小端距离为LB和LW，两者相距s=LB−LW；小端曲率半径为r.若支承点P微小扰动偏离，轴线与竖直方向夹角为小量δ，而法线仍通过曲率中心C∗(图3)，则稳定平衡的条件是浮力FB和重力FW产生回复力矩

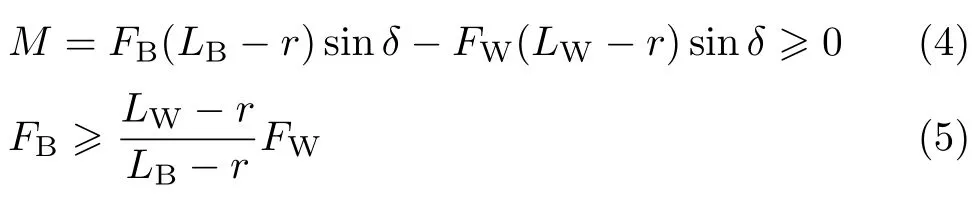
或写为

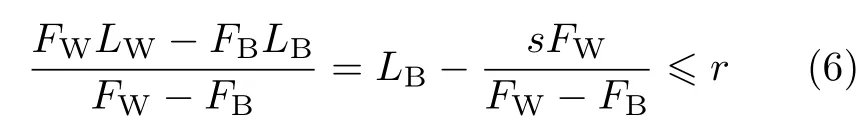
即重力与浮力的合力向下，其作用点T距小端小于曲率半径r时鸡蛋在水中稳定直立，并不需要完全浮起.

图3 竖直鸡蛋在水中稳定平衡的条件

实际称量4个新鲜鸡蛋，比重 γ为 1.068∼1.079g/cm3，因水中有 FW= γFB，由式 (6)可知合力作用点 T 从浮心 B 的偏移距离 t为(13.7∼15.7)s，但尚未达到顶点曲率中心 C∗而不能直立，平衡时轴线倾角θ在 15◦∼30◦之间，小端在下.据此可知，这些鸡蛋的s小于1mm.

鸡蛋随储存时间增加将逐渐变质，重量减小而大端气腔增加，重心移向小端，即浮心与重心的距离s增大，可在水中以小端直立.对此可略作计算.

鸡蛋完全没有气室时比重为γ0，重心与浮心重合.若鸡蛋高为2a，不考虑两端的形状差异，一端出现气室而比重为γ时，重心偏离浮心的距离s应略小于 a(γ0− γ)/γ；点 T 距浮心 t=sγ/(γ − 1) ≈a(γ0−γ)/(γ−1). 图 1右侧鸡蛋 a=27.2mm，若 γ0=1.085，则 γ=1.055时有 s=0.77mm 和t≈14.8mm；而T距小端的距离应略大于a−t=12.4mm，已与小端曲率半径14mm相当，因而鸡蛋将在水中直立.

存储约 10个月的咸鸭蛋在水中稳定平衡姿态各不相同 (图 4)，显示了质量差异而不必采用烛照检查；许多食品如菱角、荸荠等的品质，也可依据其水中浮沉来简单判断--实沉总是优于虚浮.与流体压力相比，浮力与生活有着更密切的关系，也更早得到关注[6].

图4 咸鸭蛋在水中的姿态

加入食盐可增加水的比重，从而增加浮力；鸡蛋稳定平衡的倾角将增大乃至直立和浮起--20◦C时100g水中最多可溶解氯化钠36g；农村晒酱时可据此粗略地判断盐水的浓度.与此类似，触地式欹器[7]若置于不同深度的水中，平衡姿态将随着内部水量增加出现更有趣的变化.

3 潜体的平衡

刚体密度大于液体则不能浮起，完全淹没时浮心位置是确定的.若浮心与重心重合，其稳定平衡姿态不受液体的影响，否则随浮力而变化.

浮力FB和重力FW为平行力，浮心B与重心W 相距 s；合力为 FW−FB，作用点 T在 BW 延长线上，其距浮心即形心sFW/(FW−FB)，距重心sFB/(FW−FB).将点T作为等效重心就不必考虑浮力的作用--潜体稳定平衡的条件就是：点T在支承点P处的法线上且低于其曲率中心C(图5).

另一方面，潜体稳定平衡时一定有浮力和重力对支承点P的力矩平衡

且从平衡位置发生微小变动时将引起回复力矩.

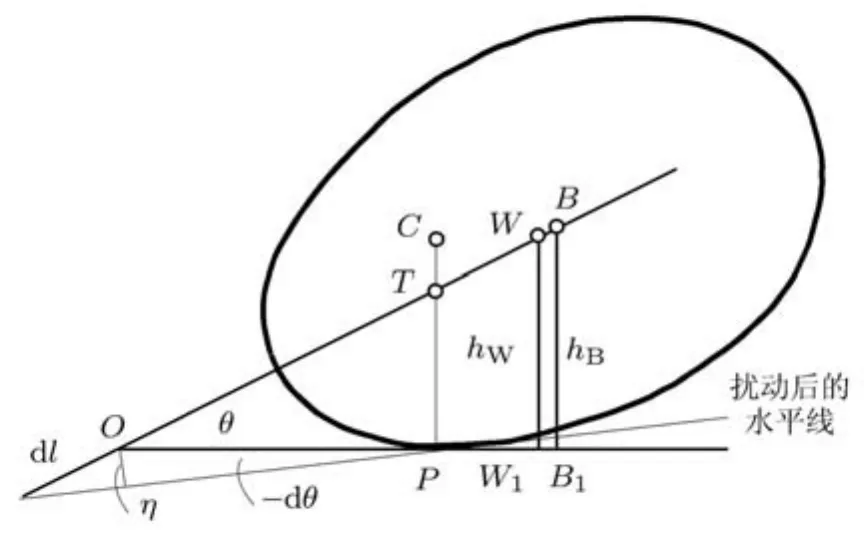
图5 潜体的稳定平衡条件

浮心B、重心W 连线与支承面相交于点O，记OW=lW，OB=lB，定义支承面为势能零线，则势能

刚体偏离平衡位置，轴线与水平面的夹角变化dθ；为图面简洁起见，将水平线转置−dθ而保持刚体位置不变(图5).倾角θ微小变动时，lW和lB的改变量相同，记为dl，有

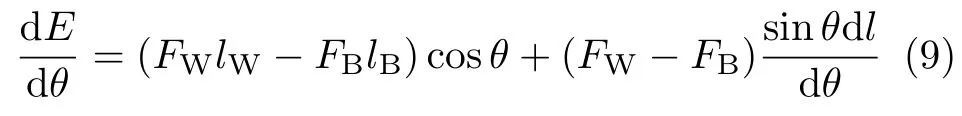
从图 5看到，η=sinθdl=OP ×(−dθ)，于是

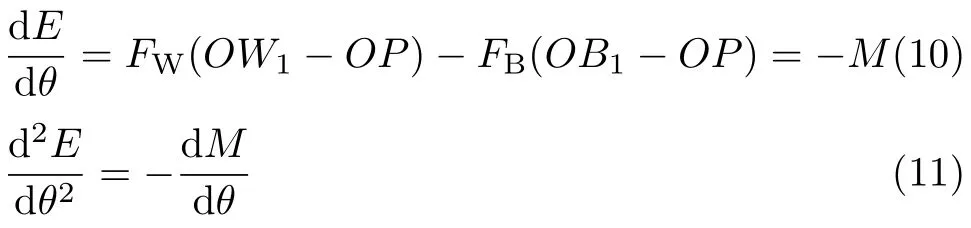
显然，力矩平衡条件 M=0就是势能达到极值；存在回复力矩的稳定平衡就是势能达到极小值[8].这是普遍结论[9]在潜体平衡中的应用，其对潜体的形状没有任何设定.当然，具体计算则需要确定或假定其形状，如文献[10]假设鸡蛋为旋转椭球.

4 讨论和结语

水洗干燥后的鸡蛋难以直立在干净玻璃、抛光石材或平整木桌之上，但依赖两三颗细小盐粒或者水滴的辅助支承即可实现大端直立.蛋在液体中姿态与浮力有关，在没有浮起之前也可以小端直立.

“稳定平衡时势能达到极小”的物理原理有多种表述形式，如刚体重心在悬挂点下方，或者重心在支承点处法线上且低于其曲率中心，以及重心与支承点的距离达到极小值[1].解决实际问题时，该原理的应用可能比力平衡分析更为简明[1112].

浮力的作用点即浮心是物体水下部分的形心.潜体的浮力和浮心是确定的，稳定平衡时也是势能达到极小值，可基于重力与浮力的合力而参照刚体分析.

浮心就是浮体的支承点，其位置随物体的姿态而变化，若高于重心则与刚体悬挂类似而总是稳定的.对于船舶而言，重心通常高于浮心乃至在水面之上；其不同姿态下浮心的全体相当于刚体外轮廓，而稳心相当于曲率中心；浮体的稳定平衡要求稳心而不是浮心高于重心.这等价于重力和浮力构成的势能极小或重心与浮心的距离极小[13].

文献 [14]称 “要保证船舶在水中的稳定性，重心必须在浮心的下方”，想来有误.作为参考，Queen Mary 2邮轮高 72m，有 17层甲板，而吃水深度10.1m(据 Wikipedia). 与此相应，长江口天然深度在6m之内；1998年起分三期进行导流潜堤等工程，2011年后在常规人工疏浚下可维持12.5m深水航道[15].

1984年朱照宣先生《非线性力学》讲义介绍，分析重心与浮心距离的极值条件得知：比重0＜λ＜1的正立方体木块在水中稳定姿态与1−λ时相同；在 0＜λ≤1/6和 1/4≤λ≤1/2时只有一个稳定平衡姿态，分别为两个面水平和一个对角线铅直，即木块与水面的交线分别为正方形和六边形；而1/6＜λ＜1/4时则有2或3个稳定平衡姿态，木块与水面交线可能是正方形、六边形、平行四边形或五边形；与水面交线是正三角形时则不可能成为稳定平衡姿态.

力学以物理为基础、以数学为工具，研究物体的受力以及运动、变形和破坏.平衡可以看作运动的特殊状态.力学问题明确而具体，物理原理清晰而简单，数学求解却复杂而烦难.

1 刘延柱.不倒翁、乌龟翻身和冈布茨.力学与实践,2010,32(2):147-149

2 刘延柱.立春时节话竖蛋.力学与实践,2013,35(1):97-98

3 http://en.wikipedia.org/wiki/EggofLi Chun

4 http://www.wikihow.com/Balance-an-Egg

5 Sasaki K.Spinning eggs--which end will rise?American Journal of Physics,2004,72(6):775-781

6 武际可.力学史杂谈.北京：高等教育出版社，2009:4-5

7 尤明庆.触地式欹器的结构特征及盈虚瓶的设计.力学与实践,2016,38(1):105-108

8 尤明庆.鸡蛋的直立及潜体的平衡.http://blog.sciencenet.cn/blog-275648-831289.html

9 朱照宣,周起钊,殷金生．理论力学(下).北京:北京大学出版社,1982:83-99

10 刘延柱.水中竖蛋与拉格朗日定理.力学与实践,2014,36(4):420-421

11 尤明庆.均匀细杆在光滑圆锥曲线壁内的稳定平衡分析.力学与实践，2016,38(2)：186-188