高温环境下二维正交编织C/SiC复合材料壁板振动模态演化

贺尔铭*,陈兵,曹存显

西北工业大学 航空学院,西安 710072

高温环境下二维正交编织C/SiC复合材料壁板振动模态演化

贺尔铭*,陈兵,曹存显

西北工业大学 航空学院,西安 710072

为了研究高温环境下二维正交编织C/SiC复合材料壁板的固有振动特性随温度的变化规律,进一步揭示模态跃迁和丢失现象。首先建立了二维正交编织复合材料的细观非均匀有限元模型,基于细观模型采用体积平均法计算得到了均匀化后材料的模量、热膨胀系数和热传导系数等宏观性能参数。在此基础上,分别研究了均匀温度和线性非均匀温度载荷下,四边简支复合材料板在屈曲前后固有频率及模态振型随温度的变化规律。研究结果表明:在均匀温度场下,如果仅考虑热载荷对材料模量的影响时,随着温度的升高,各阶固有频率逐渐降低,但降低的幅度不大;仅考虑热应力对结构刚度影响时,在临界屈曲温度后固有频率反而上升,并且随着温度的升高出现了频率交错,其对应振型发生了跃迁现象;当同时考虑热物性和热应力影响时,各阶频率值变化趋势与仅考虑热应力时类似,只是对应温度点的频率值有所下降。而在线性非均匀温度场下,通过对比不同工况下的模态振型发现,随着温度的升高某些模态振型还会出现丢失,并且这种丢失是从低阶到高阶依次发生的。

二维C/SiC;复合材料壁板;热模态;固有频率;模态跃迁和丢失现象

高超声速飞行器在某些飞行条件下会造成严重的气动加热问题,气动加热通过附面层传到结构内部导致结构温度急剧升高,使飞行器表面壁板结构面临着较为严峻的高温环境。而二维正交编织C/SiC复合材料具有高比强度、高比刚度、耐高温等优异性能,同时具有平行碳布面内力学性能相同的优点,特别适合于制备典型的热结构件,因而得到了广泛关注。高温对结构的影响主要表现在2个方面:一方面会改变材料的机械性能使材料的弹性模量降低;另一方面温度梯度导致受约束结构内部产生热应力,这些影响都会导致结构刚度发生变化,从而直接影响到结构的固有频率,因此在进行高速飞行器结构热振动分析时必须考虑温度效应的影响。

近年来,国内外许多学者开始关注壁板结构的热振动特性研究。早在1989年Spain等[1]就关注到温度升高会使结构固有频率降低的现象;随后Shukla等[2]研究了温度对复合材料曲板前10阶固有频率的影响规律,结果发现:随着温度升高,前5阶频率缓慢上升而后5阶频率却缓慢下降,并且在某一温度时各阶频率大小顺序发生了改变,即出现“频率跃迁”现象;夏巍和杨智春[3]研究了复合材料平板的热模态特性,发现屈曲前结构各阶频率都会出现下降,而且对于两对边简支的正方形复合材料板频率下降得更严重,但是其研究并未考虑到结构非线性引起的刚度非线性项,因此只适合结构发生热屈曲前的固有振动特性分析;刘芹等[4]对线性温度场作用下的层合板进行了非线性热振动分析,得到了基频随温度的变化关系,对于其他高阶固有频率随温度的变化并未进行深入研究;Singh和Panda[5]研究了考虑高阶几何非线性项时,双曲复合材料板的自由振动问题,杨莉等[6]分析了不同因素对圆柱曲板振型的影响,研究发现温度场对功能梯度材料的频率影响不大。

在实验研究方面,许多学者对不同材料板的固有频率随温度变化做了大量研究,其实验结果都表明,随着温度的升高结构的前几阶固有频率出现了下降[7-9]。史晓鸣和杨炳渊[10]通过对瞬态加热环境下变厚度板的热模态分析,发现温度使结构的固有频率出现下降,但持续加热时固有频率又会出现回升;黄世勇和王智勇[11]研究了根部固支的变厚度铝合金板的热模态,发现随着温度升高结构的固有频率出现了下降,但其并未对振型演化规律进行研究。对于模态振型的研究,Cheng等[12]通过实验分别研究了温度载荷对平板和加筋板模态振型的影响,发现随着温度的升高无论是平板还是加筋板模态振型都出现了交错现象。

上述研究虽然给出了结构固有频率与温度变化的关系,但是并未全面考虑不同参数对复合材料板固有振动特性的影响规律,而且对于频率演化的同时振型出现跃迁、丢失等这些现象并未从理论上进行研究,只有少数文献指出在实验中发现了这些现象,对于出现振型跃迁、丢失的机理也没有进行更多的分析。目前对于复合材料热振动特性的研究大多数都是基于层合板或常见的金属板,对于二维正交编织C/SiC复合材料板的很少。

本文对高温环境下二维正交编织C/SiC复合材料板的热振动特性进行了深入分析,通过细观建模得到了材料宏观等效参数并与实验值进行了对比发现误差较小,在此基础上,分别研究了均匀温度场和非均匀温度场下,四边简支复合材料壁板结构的固有频率及模态振型的演化规律。通过对温度载荷作用下复合材料板结构进行热模态分析,得到了结构振型频率随温度的变化曲线,并利用有限元仿真再现了二维正交编织材料板热振动实验中出现的模态振型跃迁及丢失现象,还运用摄动法对模态振型跃迁的机理进行了解释。

1 复合材料板的细观建模及热屈曲分析

二维正交编织复合材料内部结构复杂,其模量等性能参数随温度变化的试验数据缺乏。因此通过精确建立编织材料的细观模型,运用有限元方法模拟预测材料的宏观等效性能参数就十分必要了。本文从细观模型出发,运用均匀化假设预测了等效后的材料性能参数。在此基础上,完成了壁板结构的热屈曲分析及热模态分析。

本文所选用的复合材料细观模型是参考已有文献[13]中对二维正交编织C/SiC复合材料的建模方法,通过在扫描电镜图片中取点、拟合纤维曲线从而建立如图1所示的精确代表体积单元(RVE)模型,运用结构有限元软件PATRAN中的布尔运算得到基体模型。对于真实材料中的空隙模拟,这里是通过在有限元建模时分别在纤维束、基体以及纤维束与基体之间预制裂纹来实现的,最终得到如图2所示的有限元细观计算模型(其中纤维体积含量为40%左右,基体为45%左右,空隙为15%左右)。

图1 RVE几何模型Fig.1 RVE geometric model

图2 有限元细观计算模型Fig.2 Finite element microscopic calculation model

在对材料宏观参数进行预测时,目前使用最多的方法为通过均匀化假设将其等效为一个宏观均匀材料,并施加周期性边界条件从而得到宏观材料参数,随后将预测值与实验值进行对比,验证所建立细观模型的有效性[14-15]。本文在进行材料参数预测时也采用类似的方法,不同的是本文所建的有限元模型是基于真实电镜扫描照片,对纤维束的走势也不是简单地用折线代替。

在进行材料模量预测时,选取组分材料的弹性模量随温度T的变化如图3和图4所示[16](其中E和E0分别为某温度下和常温下材料的弹性模量),采用前面所述的细观力学方法,计算得到了不同单胞形式的等效模量参数(如表1所示,其中E11为沿着纤维方向的模量值,E33为与纤维垂直方向的模量值,其他参数方向的定义与此相同,ν为泊松比,G为剪切模量),对比发现预制孔隙后预测值与实验数据吻合良好。同时改变组分模量参数,得到了不同温度下二维正交编织C/SiC复合材料的参数,与实验值(如表2所示)相比误差较小。

使用表1中的材料属性建立了四边简支的复合材料壁板结构,其几何尺寸为:0.6 m×0.6 m×0.003 m,并采用Shell单元建立如图5所示的有限元模型。通过有限元计算得到薄板在均匀温度载荷下的临界屈曲温度为34℃。四边简支板的临界屈曲温度也可由式(1)计算。

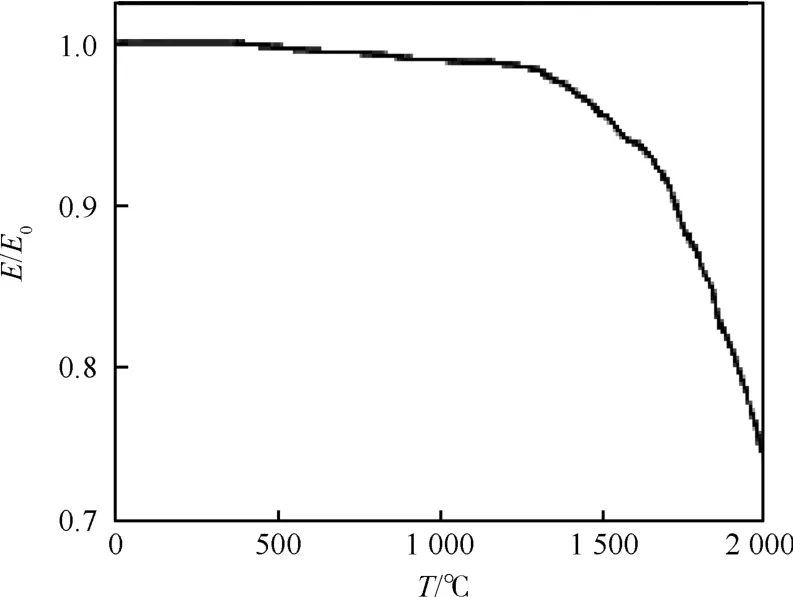
图3 纤维弹性模量随温度的变化曲线Fig.3 Curve of elastic modulus of fiber vs temperature

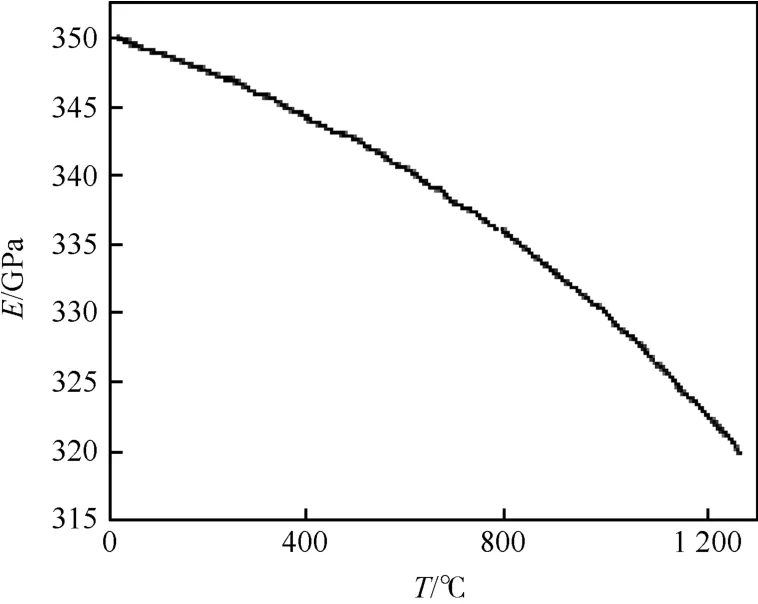
图4 SiC基体弹性模量随温度的变化曲线Fig.4 Curve of elastic modulus of SiC matrix vs temperature

表1 复合材料参数的预测值与实验值Table 1 Predictive and experimental values of composite material parameters

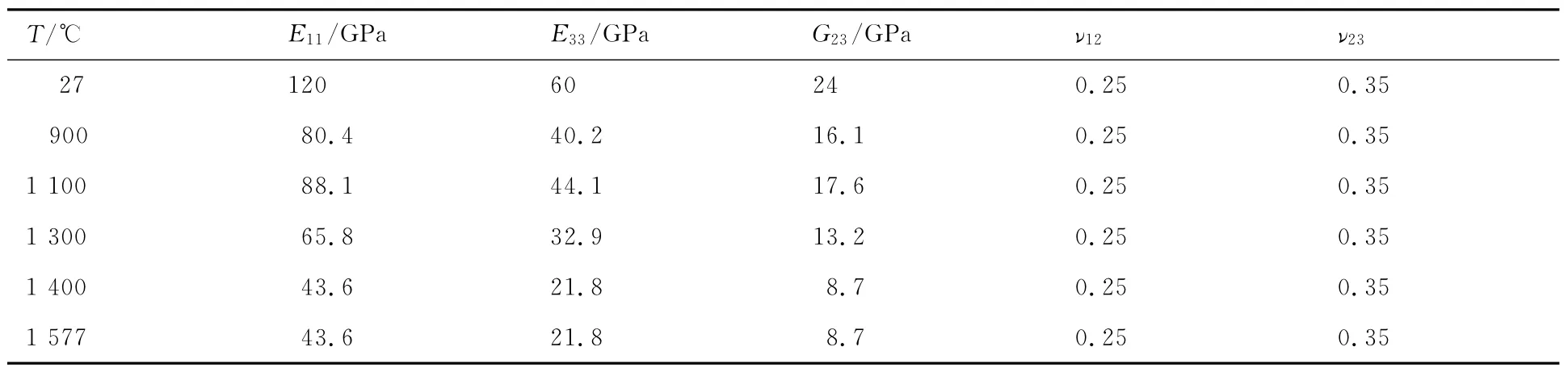
表2 不同温度下复合材料参数的实验值Table 2 Experimental value of composite material parameters at different temperatures

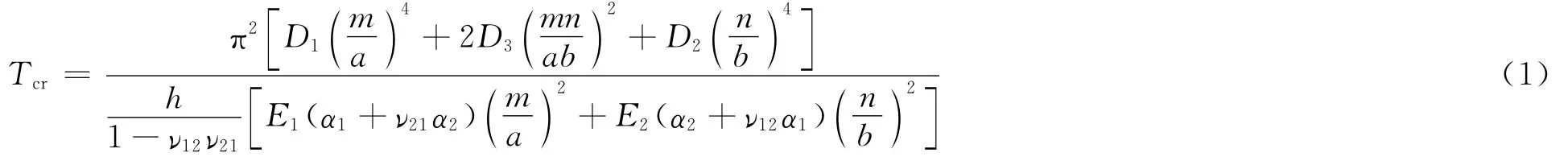
式中:a、b和h分别为薄板的长、宽和厚度;α为热膨胀系数;m、n与模态振型分布有关;D为与弹性模量、剪切模量、泊松比和板厚度有关的弯曲刚度。

由式(1)计算得到临界屈曲温度为34.31℃,与有限元计算结果十分接近。在后续热模态计算时由于温度范围变化大,涉及到屈曲前后的整个过程,这样屈曲后的热模态分析需重新建模。这里提取特征值屈曲分析得到的1阶屈曲模态,将其以1%的比例更新到结构中,通过计算得到该结构的屈曲平衡路径如图6所示。

图5 壁板有限元模型Fig.5 Finite element model of panel

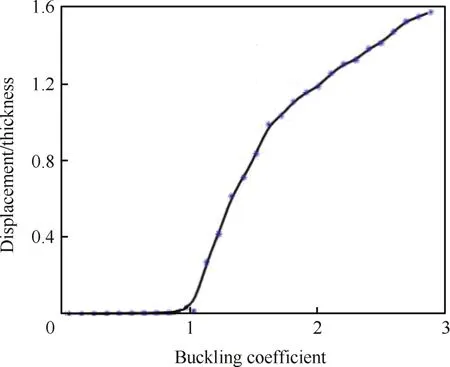
图6 简支板屈曲平衡路径Fig.6 Buckling equilibrium path of simply-supported plate

由图6可见,屈曲前结构的法向位移较小,屈曲后法向位移突然增加,但是增加的幅度越来越缓,在临界屈曲载荷后由于结构刚度有所增大,所以法向位移增加变缓。通过对复合材料壁板的屈曲分析,可以得到不同温度载荷下的热应力和应变场,在后面的热振动模态分析时可以直接将得到的应力应变场作为载荷引入进来。

2 壁板结构热模态分析

温度载荷对结构模态的影响主要表现在2个方面:①温度的改变会使材料的弹性模量发生变化,随着温度的增加材料的弹性模量会下降[17-19];② 温度梯度的出现会使结构内部产生变形从而产生热应力。材料特性的下降和热应力都会导致结构刚度出现变化,从而直接影响到结构的固有频率以及振型分布,因此,在后面的热模态分析时本文主要也是从这两方面出发的。

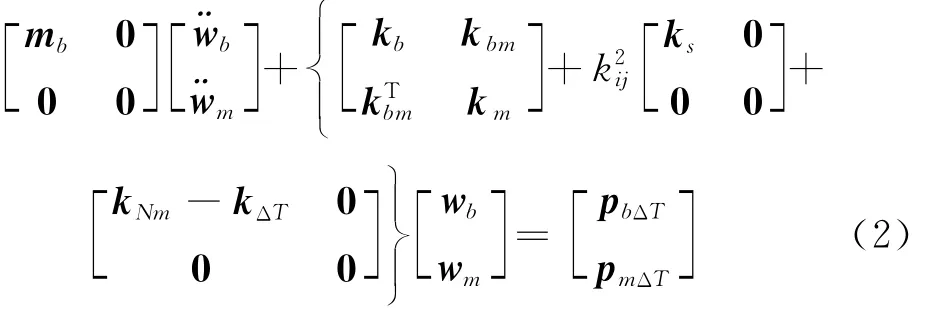
Malekzadeh等[20]利用Hamilton原理推导出了系统在热环境下的运动方程,本文基于能量原理和变分方法的Hamilton原理,建立复合材料壁板在热环境下的振动方程为式中:ks为剪切刚度;kij为剪切矫正因子;mb和kb分别为平板结构的质量矩阵和刚度矩阵;km为温度引起的刚度变化;kbm为耦合刚度项;wm为结构的位移场;wb为平板的位移场;kNm为结构的面内位移在弯曲自由度上的附加刚度;kΔT为温度应变在板弯曲自由度上的附加刚度;pbΔT和pmΔT分别为温度载荷引起的附加力和附加力矩。

对于正交各向异性的复合材料平板结构,刚度矩阵中的耦合刚度项kbm=0,并且有pbΔT=0,则式(2)可以变为

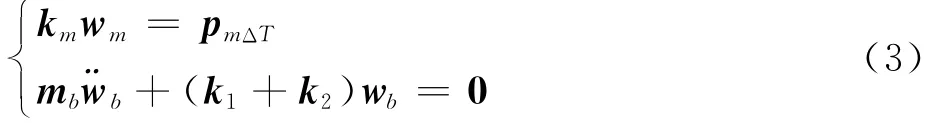
式中:k1=kb+k2ijks为不计及温度影响的复合材料壁板结构的刚度矩阵;k2=kNm+kΔT为由于温度载荷引起的刚度矩阵的修正项。

在实际的求解中,首先求出式(3)中的第1个静力学方程,得到结构的位移场wm,并将结构变形施加到结构上,即为动力学分析的刚度矩阵引入了修正项k2,在此基础上就可以对某一特定温度场下复合材料壁板的振动特性进行分析,这样就在动力学分析中考虑了热效应的影响。

2.1 均匀温度载荷下壁板结构热模态分析

在均匀温度场下进行模态分析时,本文从3个方面综合考虑了热物性和热应力对结构热模态的影响:① 仅考虑热载荷引起的材料弹性模量变化时,结构固有频率以及模态振型的变化规律;② 仅考虑由热载荷引起的热应力时,结构固有频率以及模态振型的变化规律;③ 综合考虑两种因素时,结构固有频率以及模态振型的变化规律。在进行热模态分析时,选取参考温度为T=20℃,选取的结构为进行屈曲分析后更新过的有限元模型,采用有限元分析软件ANSYS,通过定义材料属性表来实现材料模量等随温度的变化,进行热分析得到温度分布、热应力等数值,随后运用该软件的模态分析模块进行热模态分析。

只考虑温度载荷对材料参数的影响时,计算得到前10阶频率f随温度T的变化如图7所示,其中部分阶次曲线完全重合。可以看出,各阶频率随着温度的升高而降低,但没有出现频率交错现象,而且频率降低幅度也比较小,当温度升高到1 000℃ 时1阶频率也只下降了9.3 Hz。可以发现,在1 000℃附近频率随着温度的增加反而增加,从表2中数据可看出这是由于该温度范围内材料模量随温度升高而增加导致的。

仅考虑温度载荷对模量影响时得到的频率随温度变化不是很明显,为了区别不同因素对结构固有频率变化规律的影响,仅考虑热应力影响时选取弹性模量为一常数。计算时仅考虑热载荷引起的热应力对结构模态变化规律的影响。

图8为仅考虑热应力时前10阶频率随温度的变化曲线。从图中可以看出在临界屈曲温度前,各阶固有频率均随着温度的升高而降低,且幅度比较大;达到临界屈曲温度时,复合材料板趋于失稳,第1阶频率接近于零;跨过临界屈曲温度后,前6阶频率开始升高且在临界屈曲温度附近增幅较大,同时随着温度的升高出现了频率交错现象,且某些相同阶次的频率值不再相同。

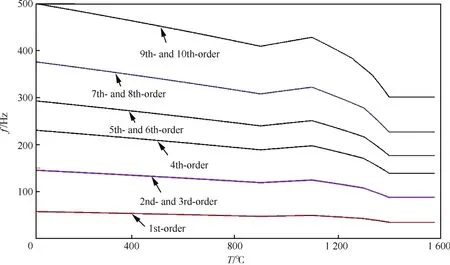
图7 仅考虑热物性时频率随温度的变化曲线Fig.7 Frequency-temperature curves when only considering effect of temperature on elastic modulus

图9～图11给出了不同温度下前6阶的模态振型,对比图9和图10、图10和图11中的振型演化顺序发现,临界屈曲温度后结构模态发生了跃迁现象(如图12所示)。在247℃时,第1阶与第2阶振型次序发生了交换,从图8中也可以看出在403℃附近也出现了一次跃迁。当温度达到1 000℃时,第1阶振型和第2阶振型又出现了交错,这与图8是吻合的。这些跃迁现象表明:在温度载荷作用下,复合材料板的模态振型会出现交错,也就是说温度载荷会使高阶模态振型提前出现。这里还给出了1 100℃时前6阶模态振型(如图13所示),从图中可以看出此时振型变化已经十分复杂。

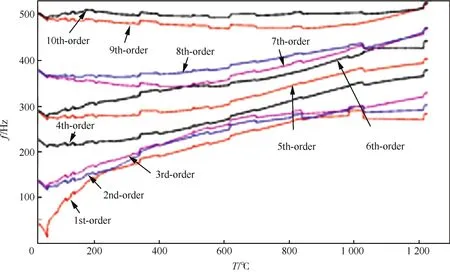
图8 仅考虑热应力时频率随温度的变化曲线Fig.8 Frequency-temperature curves when only considering thermal stress

图9 29℃时前6阶模态振型图(仅考虑热应力)Fig.9 First six vibration mode shapes at 29℃(when only considering thermal stress)

图10 247℃时前6阶模态振型图(仅考虑热应力)Fig.10 First six vibration mode shapes at 247℃(when only considering thermal stress)

图11 403℃时前6阶模态振型图(仅考虑热应力)Fig.11 First six vibration mode shapes at 403℃(when only considering thermal stress)

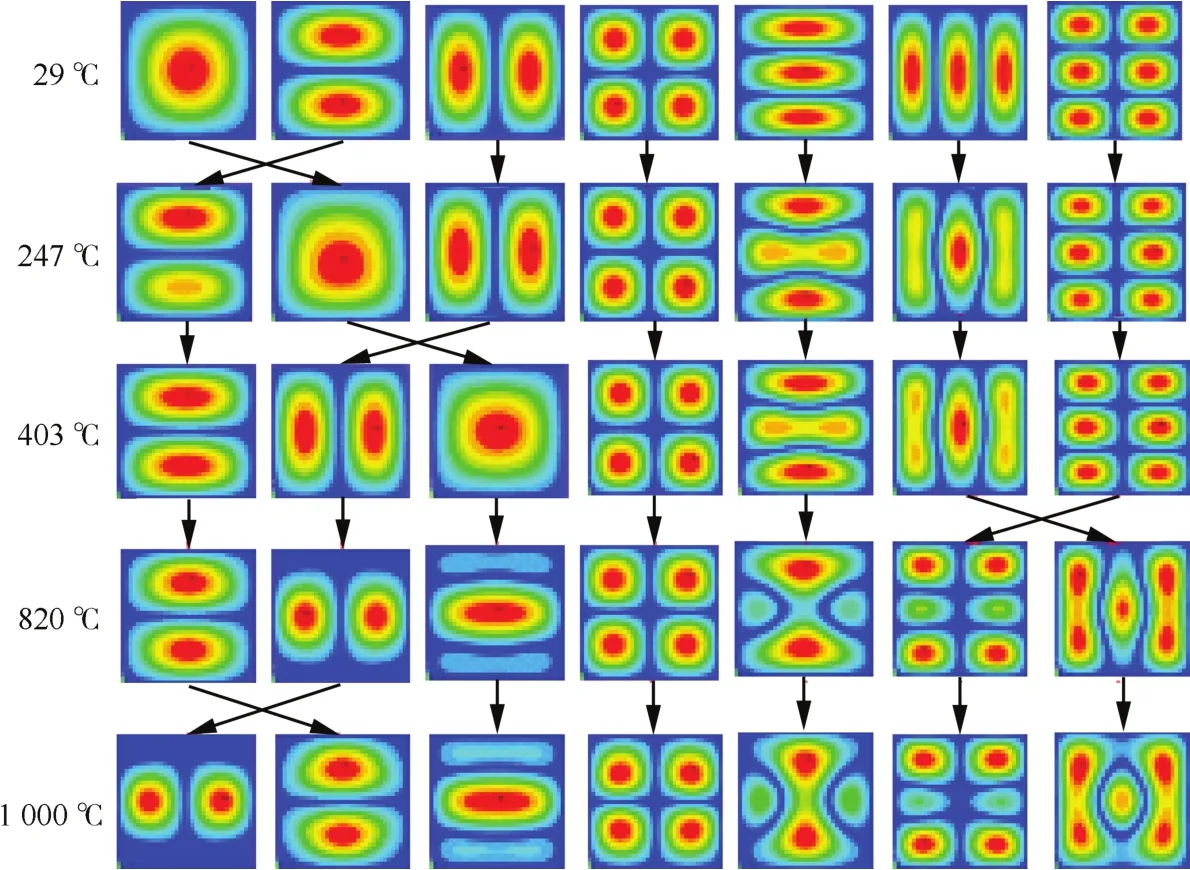
图12 模态跃迁现象Fig.12 Mode jumping phenomenon

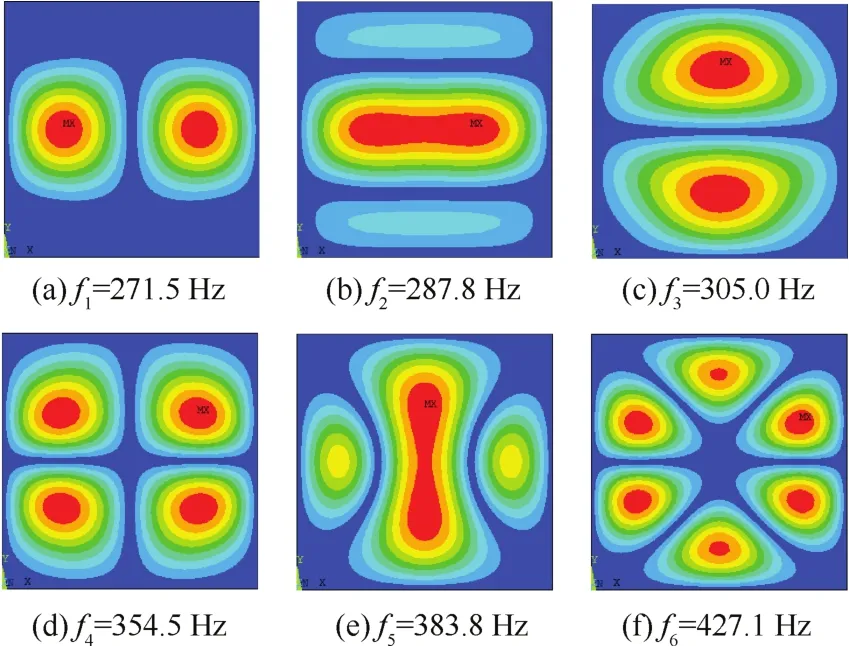
图13 1 100℃时前6阶模态振型图(仅考虑热应力)Fig.13 First six vibration mode shapes at 1 100℃(when only considering thermal stress)

从式(1)中可以看出,四边简支壁板结构的临界屈曲温度不仅与材料的特性、尺寸等参数有关,还与模态振型分布有关。笔者在Nastran非线性模块下进行了热模态分析,得到了不同阶次频率对应的临界屈曲温度,但是由于该情况在工程实际中并未得到广泛认可,因此此处不再进行深入研究,仅给出部分阶次频率随温度的变化曲线,如图14所示。

综合考虑温度对材料参数和热应力的影响时,计算得到频率随温度的变化曲线如图15所示,与仅考虑热应力时的结果(图8所示)对比可以发现,当温度较低时模量的变化对频率的影响比较小,但是在温度较高时由于模量的降低导致频率出现了明显的变化,但也只是在各个温度点处频率值出现了下降,模量变化对结构整体模态振型变化趋势的影响不大。

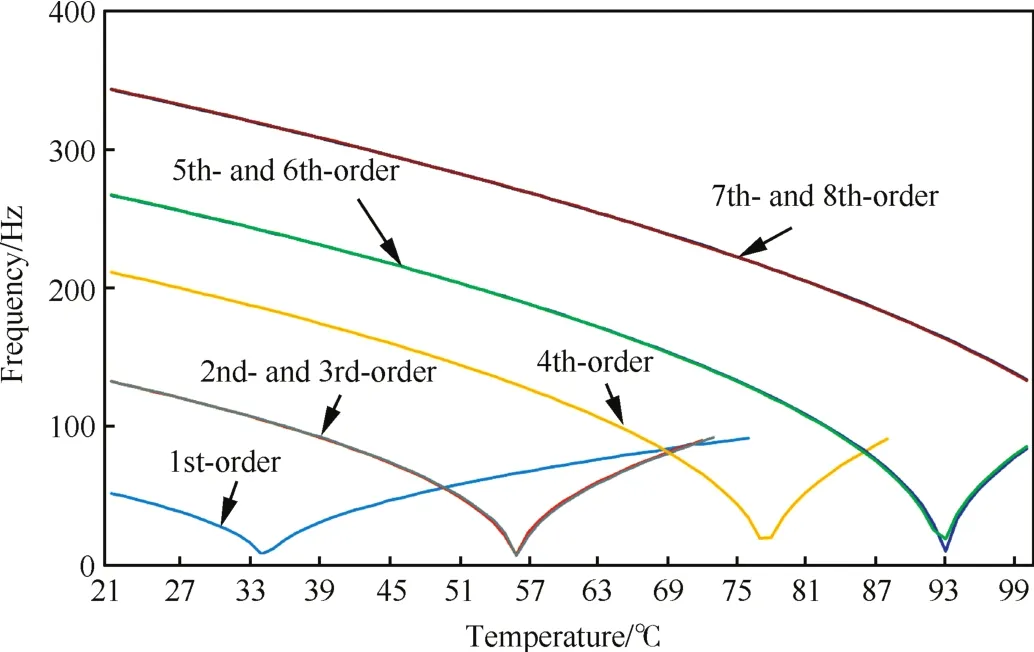
图14 考虑后屈曲时各阶频率随温度变化曲线Fig.14 Frequency-temperature curves when considering post buckling

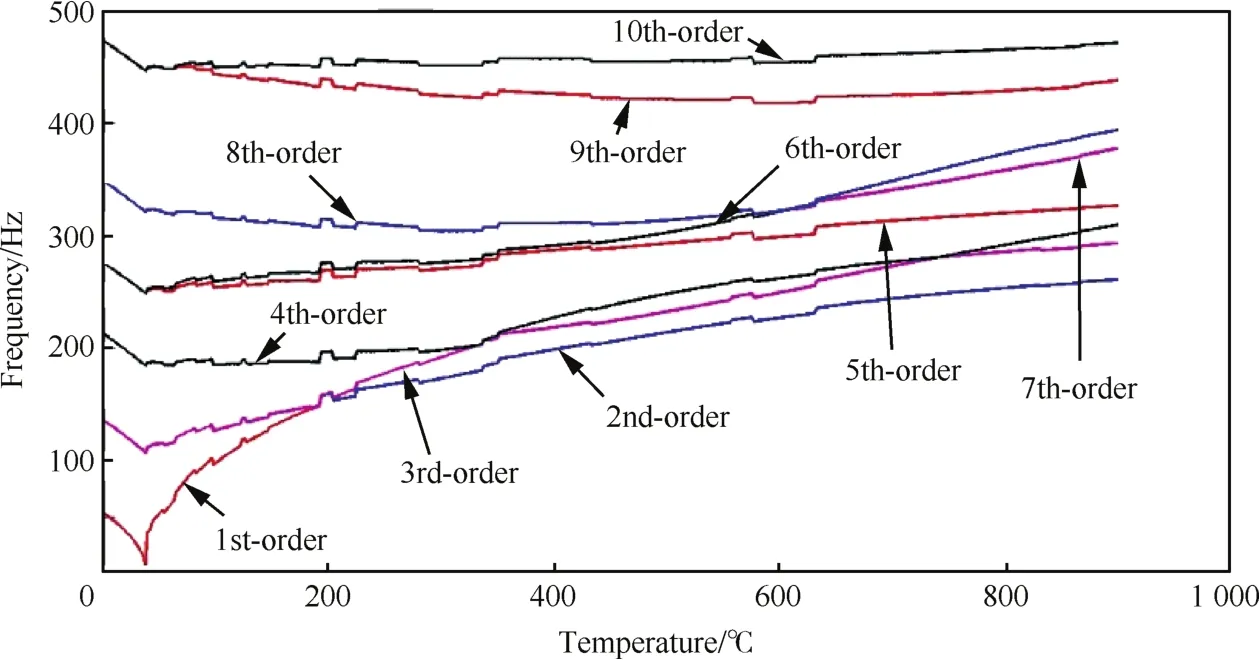
图15 同时考虑热应力和热物性时频率随温度的变化曲线Fig.15 Frequency-temperature curves when considering thermal stress and effect of temperature on elastic modulus

2.2 非均匀温度场下壁板结构热模态分析

在对非均匀温度场下的壁板结构进行热模态分析时选取的参考温度为T=20℃,首先在板的两端施加表3所示的不同温度边界条件,进行热分析得到温度分布,随后将得到的温度场以载荷的形式施加在结构上,再对整体结构进行静力学分析得到应力场,再将得到的热应力场作为初始边界条件施加在结构上进行模态分析。

计算得到不同工况下的模态振型如图16所示,对比图中振型发现:随着x=l边温度的增加,模态振型出现了丢失现象,工况3时1阶模态振型不再是1个半波的振型,变为2个半波的振型,工况5时1阶振型已经变为4个半波的振型。随着边界温度的增加,振型丢失也越来越严重。但是值得注意的是,这种丢失不是杂乱的,而是按照从低阶到高阶的顺序依次丢失的。

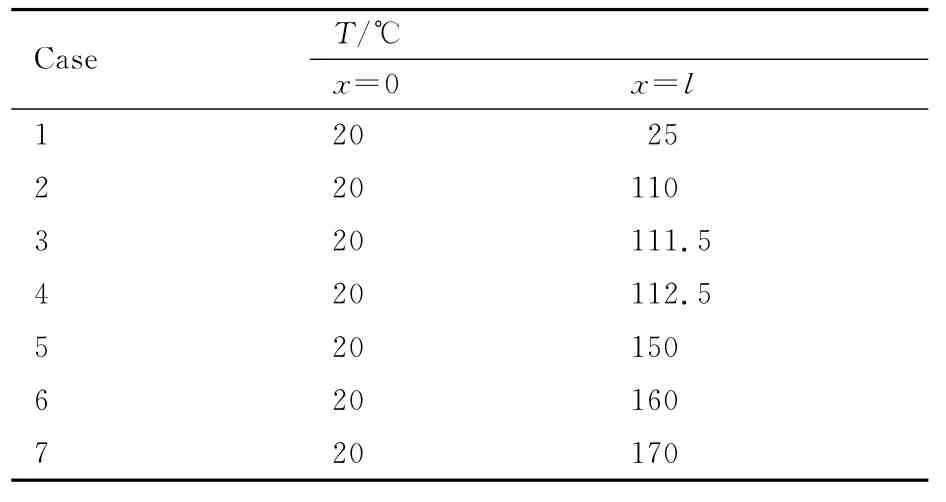
表3 非均匀的线性温度载荷工况Table 3 Non-uniform linear temperature loads

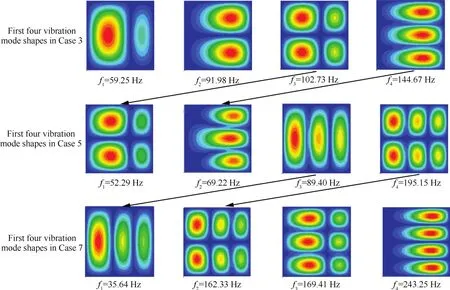
图16 不同温度下的模态振型丢失Fig.16 Vibration mode shape losing under different thermal conditions

在线性非均匀温度场下,随着温度的升高振型丢失越来越严重。结构处于较高的基础温度环境时,结构的模态振型出现了更复杂的变化。这里给出了2种不同的工况(如表4所示),计算得到了这2种工况下的模态振型如图17和图18所示,由于此时模态振型变化复杂,这里仅给出了前4阶振型。对比图17和图18可以发现,当整体环境温度较高时,也会出现振型丢失现象。

表4 不同温度载荷工况Table 4 Different temperature load conditions

图17 工况A时前4阶模态振型Fig.17 First four vibration mode shapes in Case A

图18 工况B时前4阶模态振型Fig.18 First four vibration mode shapes in Case B

3 模态跃迁和丢失机理分析

结构模态的跃迁及丢失现象以往主要发生在一些模态密集结构,像大型空间网壳、网架、索穹顶结构、叶片轮盘等具有周期对称特点的结构。这些结构由于其基频较低且模态比较密集,很小的参数扰动就有可能导致某些模态阶次的跃迁。在研究此类结构模态跃迁的机理时,应用较多的还是摄动法,将外界因素的影响作为一个小参数摄动引入振动特征方程,通过分析摄动前后特征值的变化来解释模态跃迁的机理。

下面就基于摄动法分析,对随着环境温度的升高上述复合材料简支板的模态跃迁机理作出解释。

在不考虑阻尼时,系统振动的特征方程为

式中:各量均为未受到热载荷之前的原始结构物理量;K0和M0分别为结构的刚度矩阵和质量矩阵;λ(i)0为第i阶特征值,即固有频率,u(i)0为该特征值对应的特征向量,即固有模态振型。

当结构受到高温载荷后,结构的质量、刚度矩阵都会发生变化,在这里引入一个微小量ε,用它

来表示温度载荷对质量、刚度矩阵的改变,这样变化后的质量矩阵和刚度矩阵可以表示为

式中:εK1和εM1分别为刚度矩阵和质量矩阵的变化量,下标1表示1阶摄动。当质量矩阵和刚度矩阵由于温度变化而发生改变时,对应的特征值和特征向量也发生了变化。将特征值和特征向量按ε展开成幂级数,有

其中:u(i)1和λ(i)1分别为特征向量和特征值的1阶摄动量,对于2阶及更高阶摄动量这里当作小量不予以考虑。将得到的式(5)～式(8)代入式(4)中可以得到:

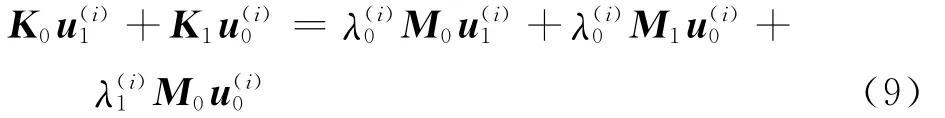
根据展开定理,将u1(i)在原系统的特征向量u(s)0上展开则可以得到:

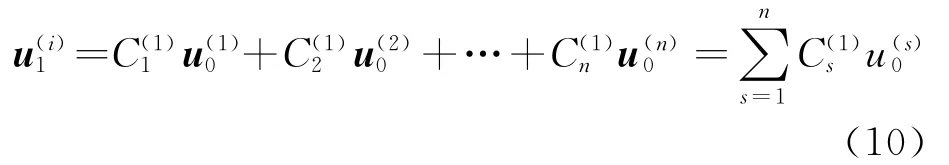
将原系统的特征矢量归一化为

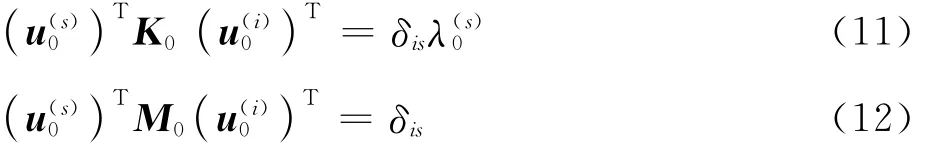
将式(10)代入式(9)可以得到特征值的1阶摄动表达式为

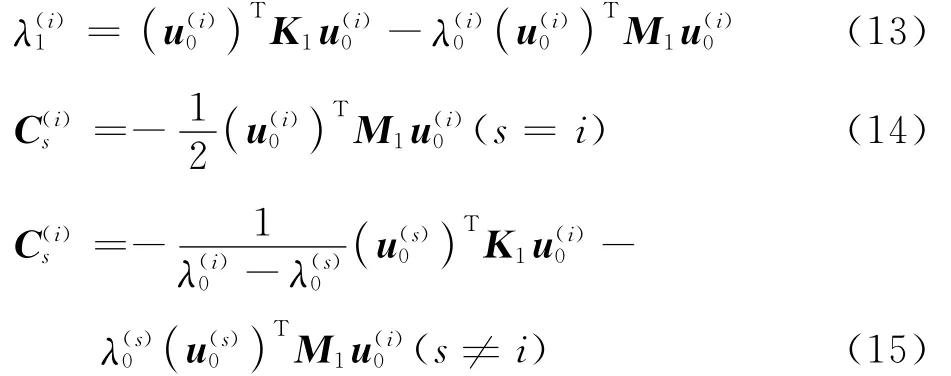
从式(13)可以看出,相同的参数摄动对不同

阶次特征值的摄动结果却是不相同的。当相邻的2个特征值满足λ0(i)≤λ0(i+1),并且1阶摄动满足ε(λ1(i)-λ1(i+1))＞λ0(i)-λ0(i+1)时,就可以得到λ(i)≥λ(i+1)。而在振动分析时,对于模态的阶次是严格按照特征值(固有频率)大小由小到大排列的,所以摄动后频率的变化导致低阶模态频率高于高阶模态频率,即发生了模态跃迁现象。

4 结 论

本文研究了高温环境下二维正交编织C/SiC复合材料简支板的固有振动特性,通过分析不同因素对结构固有频率的影响,得到了不同温度下结构固有频率随温度的变化曲线,同时还对结构模态振型的演化规律进行了深入研究。利用有限元法仿真重现了在高温环境下复合材料壁板结构振动实验中出现的模态振型跃迁及丢失现象,并运用摄动理论对这些现象的发生机理进行了解释。得到以下结论:

1)均匀温度场下,仅考虑材料参数随温度变化时,二维正交编织C/SiC复合材料板各阶固有频率有所下降,但是下降的幅度比较小。

2)假设材料参数为一定值,仅考虑热应力对结构刚度影响时,二维正交编织C/SiC复合材料板在临界屈曲温度(34℃)下前10阶固有频率随着温度升高而降低;而在临界屈曲温度后,随着温度升高结构固有频率又开始增加。在大约247℃和403℃附近发生了2次模态振型跃迁现象。从图8还可以看出在850℃附近,第1、2阶振型又出现了交错现象,即高阶模态振型在较低阶频率处出现。

3)与仅考虑热应力时的结果相比,综合考虑热物性和热应力时结构各阶频率值在每个温度点有所下降而且随着温度的升高下降幅度更加明显,但是总体变化趋势和仅考虑热应力时是一致的。

4)在线性非均匀温度场下,当基础温度较低时,随着温度升高复合材料壁板结构的低阶模态振型出现了丢失,高阶模态振型提前出现,而且这种模态丢失现象是按照由低阶振型到高阶振型的顺序依次发生的。当基础温度较高时,前面的很多阶振型都已丢失。与较低基础温度下的振型相比,此时的模态振型也更为复杂。

[1] SPAIN C V,SOISTMANN D L,LINVILLE T W.Integration of thermal effects into finite element aero-thermoelastic analysis with illustrative results[C]//Sixth National Aero Space Plane Technology Symposium,1989:Paper No.9.

[2] SHUKLA A,GORDON R W,HOLLKAMP J J.Numer-ical investigation of the snap-through response of a curved,clamped-clamped plate with thermal and random loading[C]//AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,AIAA/ASME/ASCE/AHS/ASC Adaptive Structures Conference 10th.Reston:AIAA,2008.

[3] 夏巍,杨智春.热环境下复合材料壁板的振动特性分析[J].应用力学学报,2005,22(3):359-363.XIA W,YANG Z C.Vibration analysis to composite panels in thermal environment[J].Chinese Journal of Applied Mechanics,2005,22(3):359-363(in Chinese).

[4] 刘芹,任建亭,姜节胜,等.复合材料层合板非线性热振动分析[J].动力学与控制学报,2005,3(1):78-83.LUI Q,REN J T,JIANG J S,et al.Nonlinear thermal vibration characteristic analysis composite laminated plates[J].Journal of Dynamics&Control,2005,3(1):78-83(in Chinese).

[5] SINGH V K,PANDA S K.Nonlinear free vibration analysis of single/doubly curved composite shallow shell panels[J].Thin-Walled Structures,2014,85:341-349.

[6] 杨莉,郝育新,杨绍武,等.热环境下FGM圆柱曲板的模态分析[J].材料热处理学报,2014,35(8):198-205.YANG L,HAO Y X,YANG S W,et al.Modal analysis of functionally graded cylindrical panel in thermal field[J].Transactions of Materials&Heat Treatment,2014,35(8):198-205(in Chinese).

[7] GENG Q,LI H,LI Y.Dynamic and acoustic response of a clamped rectangular plate in thermal environments:Experiment and numerical simulation[J].Journal of the Acoustical Society of America,2014,135:2674-2682.

[8] 吴大方,王岳武,蒲颖,等.高超声速飞行器复合材料翼面结构1 100℃高温环境下的热模态试验[J].复合材料学报,2015,32(2):323-331.WU D F,WANG Y W,PU Y,et al.Thermal modal test of composite wing structure in high-temperature environments up to 1 100℃for hypersonic flight vehicles[J].Acta Materiae Compositae Sinica,2015,32(2):323-331(in Chinese).

[9] 程昊,吴振强,李海波,等.高温环境下典型结构热模态分析[C]//北京力学会第20届学术年会.北京:力学学会,2014.CHENG H,WU Z Q,LI H B,et al.Modal analysis of typical structure in hot environment[C]//The 20th Annual Meeting of Beijing Society of Theoretical and Applied Mechanics.Beijing:Beijing Society of Theoretical and Applied Mechanics,2014(in Chinese).

[10] 史晓鸣,杨炳渊.瞬态加热环境下变厚度板温度场及热模态分析[J].计算机辅助工程,2006,15(B09):15-18.SHI X M,YANG B Y.Temperature field and mode analysis of flat plate with thermal environment of transient heating[J].Computer Aided Engineering,2006,15(B09):15-18(in Chinese).

[11] 黄世勇,王智勇.热环境下的结构模态分析[J].导弹与航天运载技术,2009,29(5):50-52.HUANG S Y,WANG Z Y.The structure modal analysis with thermal environment[J].Missiles&Space Vehicles,2009,29(5):50-52(in Chinese).

[12] CHENG H,LI H B,ZHANG W,et al.Effects of radiation heating on modal characteristics of panel structures[J].Journal of Spacecraft&Rockets,2015,52(4):1-8.

[13] 吕毅.平纹编织C/SiC复合材料力学性能的数值模拟[D].西安:西北工业大学,2009:40-51.LV Y.The numerical simulation of the mechanical properties of plain weave C/SiC composites[D].Xi'an:Northwestern Polytechnical University,2009:40-51(in Chinese).

[14] 张超,许希武,郭树祥.二维二轴1×1编织复合材料细观结构模型及力学性能有限元分析[J].复合材料学报,2011,28(6):215-222.ZHANG C,XU X W,GUO S X.Microstructure model and finite element analysis of mechanical properties of 2D 1×1 biaxial braided composites[J].Acta Materiae Compositae Sinica,2011,28(6):215-222(in Chinese).

[15] 严雪,许希武,张超.二维三轴编织复合材料的弹性性能分析[J].固体力学报,2013,34(2):140-151.YAN X,XU X W,ZHANG C.Analysis of elastic properties of 2D triaxial braided composites[J].Chinese Journal of Solid Mechanics,2013,34(2):140-151(in Chinese).

[16] 张歌,张程煜,乔生儒,等.2D-C/SiC高温弹性模量的预测[J].机械强度,2013,35(1):94-99.ZHANG G,ZHANG C Y,QIAO S R,et al.Prediction of elastic modulus at elevated temperature for 2D-C/SiC[J].Journal of Mechanical Strength,2013,35(1):94-99(in Chinese).

[17] WANG H L,ZHANG C Y,LIU Y S,et al.Temperature dependency of interlaminar shear strength of 2D-C/SiC composite[J].Materials&Design,2012,36:172-176.

[18] 马彦,陈朝辉.1 800℃热处理对PIP法C/SiC复合材料结构和性能的影响[J].材料工程,2015,43(4):98-101.MA Y,CHEN Z H.Effect of 1 800℃annealing on microstructures and properties of C/SiC composites fabricated by precursor infiltration and pyrolysis[J].Journal of Materials Engineering,2015,43(4):98-101(in Chinese).

[19] SUN Z,CHEN X,SHAO H,et al.Numerical modeling of oxidized 2D C/SiC composites in air environments below 900℃:Microstructure and elastic properties[J].Applied Composite Materials,2016,23(4):1-21.

[20] MALEKZADEH P,SHAHPARI S A,ZIAEE H R.Three-dimensional free vibration of thick functionally graded annular plates in thermal environment[J].Journal of Sound and Vibration,2010,329(4):425-442.

Vibration mode evolution of 2D woven C/SiC composite panels in hot environment

HE Erming*,CHEN Bing,CAO Cunxian

School of Aeronautics,Northwestern Polytechnical University,Xi'an 710072,China

To study the law of the variation of natural vibration frequencies of 2D woven C/SiC composite panels in hot environment,and further reveal the mode jumping and losing phenomena in the thermal mode test,the mechanics modules,thermal expansion coefficient and thermal conductivity of 2D woven C/SiC composite panels after homogenization are calculated by volume-averaged method based on its microscopic mechanics model.The vibration mode evolutions of the simply-supported rectangular panel under uniform temperature loads and linear non-uniform temperature loads are studied based on the macroscopic material properties obtained above,and the relationships between high temperature and the natural frequency,mode shapes are obtained from the mode analysis.The research results show that under the uniform temperature loads,when we consider only the effect of temperature on the elastic modulus,the natural frequency decrease slightly as the temperature increases.When the thermal stress caused by high temperature is considered separately,it is found that the natural frequency increases after the critical buckled temperature,and as the temperature increases,the mode shape being staggered which results in some mode shapes appear early,in other words,mode jumping occurs in those moments.lf both of the two factors are considered,the natural frequency will be smaller at each temperature compared with only considering the thermal stress caused by high temperature.However,the trends are similar.Under the non-uniform high temperature loads,it shows that some modal shapes may be lost by comparing the mode shapes under different operating conditions,and the loss is not messy,but goes from low-order to high-order frequency.

2D C/SiC;composite panel;thermal mode;natural frequency;mode jumping and losing phenomenna

2016-06-22;Revised:2016-10-19;Accepted:2017-03-07;Published online:2017-04-01 13:32

URL:www.cnki.net/kcms/detail/11.1929.V.20170401.1332.006.html

s:National Natural Science Foundation of China(51675426);Aerospace Science and Technology lnnovation Fund(2014KC010043)

V214.8

A

1000-6893(2017)07-220553-12

10.7527/S1000-6893.2017.220553

2016-06-22;退修日期:2016-10-19;录用日期:2017-03-07;网络出版时间:2017-04-01 13:32

www.cnki.net/kcms/detail/11.1929.V.20170401.1332.006.html

国家自然科学基金(51675426);航天科技创新基金(2014KC010043)

*通讯作者.E-mail:heerming@nwpu.edu.cn

贺尔铭,陈兵,曹存显.高温环境下二维正交编织C/SiC复合材料壁板振动模态演化[J].航空学报,2017,38(7):220553.HE EM,CHENB,CAO C X.Vibration mode evolution of2D woven C/SiC composite panels in hot environment[J].Acta Aeronuatica et Astronautica Sinica,2017,38(7):220553.

(责任编辑:徐晓)

*Corresponding author.E-mail:heerming@nwpu.edu.cn