基于梯度增强型Kriging模型的气动反设计方法

韩少强,宋文萍,韩忠华*,王乐

西北工业大学 航空学院 翼型叶栅空气动力学国家级重点实验室,西安 710072

基于梯度增强型Kriging模型的气动反设计方法

韩少强,宋文萍,韩忠华*,王乐

西北工业大学 航空学院 翼型叶栅空气动力学国家级重点实验室,西安 710072

基于Kriging模型的代理优化算法目前在气动优化设计中得到了广泛应用。但在高维(设计变量大于30个)气动优化中,计算量过大的问题对其进一步发展产生了严重制约。将翼型和机翼气动反设计问题转化为优化问题,采用Adjoint方法进行快速梯度求解,利用基于梯度增强型Kriging(GEK)模型的代理优化算法分别开展了18、36和108个设计变量的气动反设计。首先,通过采用在设计空间局部建立GEK模型的方法成功地将基于代理优化算法的气动反设计问题的维度拓展到了100维以上。其次,研究了梯度计算精度对基于GEK模型的反设计的影响,发现梯度精度越高,反设计的最终效果越好,同时效率相当。最后,通过不同维度的气动反设计算例,比较了改进拟牛顿法(BFGS)、基于GEK模型和Kriging模型的代理气动反设计方法,结果表明基于GEK模型的代理优化算法的效率大幅度高于基于Kriging模型的代理优化算法,并且维度越高,效率优势越明显;同时,基于GEK模型的代理优化算法在优化效果及分析程序调用次数上相比于BFGS方法也略有优势。

设计优化;Kriging;梯度增强型Kriging(GEK);代理模型;BFGS;翼型反设计;机翼反设计

Kriging模型具有较好预测非线性、多峰值函数的能力,且能给出未知点预测值的误差估计。因此,Kriging代理优化算法[1-2]受到了广泛的重视。近年来,Kriging模型被越来越多地应用于气动及多学科优化设计中[3-8],在得到优良的设计结果的同时大大减少了优化设计所需要的计算时间。另一方面,相对于优化方法,反设计方法具有计算效率高、针对性强和可信度高等特点[9],在飞行器气动设计领域仍然是不可或缺的[10]。目前Kriging代理优化算法在气动反设计中的应用较少,并且以设计变量个数较少的翼型反设计为主。Toal等[11-12]通过翼型反设计,着重比较了使用不同优化算法优化Kriging超参数对最终反设计结果的影响。但是他们并非着眼于Kriging代理优化算法在翼型反设计中的应用研究,也未能得到真正有效的反设计结果。刘俊等[13]将翼型气动反设计问题转化为优化设计问题,利用Kriging代理优化算法进行了翼型的单目标、多目标气动反设计;研究了模型加点准则对设计结果的影响;并和多项式响应面模型优化方法进行了比较研究。结果表明,Kriging代理优化算法的优化效果和效率都明显优于基于多项式响应面的优化方法。

随着人们对设计结果的性能要求以及可信度要求的提高,一方面更高可信度的数值模拟程序被应用于飞行器的气动设计中,这就意味着单次数值模拟所需的计算花费将急剧增长。另一方面随着设计变量个数(设计空间维度)的增加,Krig-ing模型精确建模所需要的CFD调用次数呈指数增长[14],这种现象又被称为“维度之咒”。对于机翼甚至更复杂的三维外形优化,设计变量多,Kriging优化过程需要大规模调用耗时的CFD分析。因此,针对高维问题亟待发展更加高效的气动优化设计方法。

为了提高Kriging代理优化效率,梯度增强型Kriging(Gradient-Enhanced Kriging,GEK)模型在Kriging模型中引入梯度信息,即在建立代理模型时除了利用样本点处的函数值,同时还要利用样本点处的梯度值,从而提高模型的精度。这样,建立和Kriging模型相同精度的GEK模型,需要的样本点数量将大大减少。在气动设计领域,当前已具备高效计算梯度的技术——Adjoint方法[15-17],只需额外花费一次与CFD相当的计算量即可获得目标函数对所有设计变量的梯度。也就是说,当使用高效梯度计算方法时,建立相同样本点数的GEK模型只需比Kriging模型增加较少的计算量,而建模精度却可以得到大幅度提高,从而充分发挥GEK模型的优势。Liu[18]和Chung[19]等分别提出了一种间接GEK模型和一种直接GEK模型。间接GEK模型利用一阶泰勒展开将梯度值变成附加样本点的函数值,然后按常规Kriging模型方法建立近似模型。GEK模型直接将样本点的梯度值和样本点的函数值一起加权到模型的预测值中。Laurenceau等[20-21]比较了Kriging、直接GEK、间接GEK模型在气动问题中的预测精度,发现在相同样本点数下两种GEK模型的精度都高于Kriging模型。Han等[22]发展了一种更一般化的直接GEK模型,允许梯度信息在任意位置引入,且允许在某些样本点处不使用梯度信息。Han等在此基础上,又发展了一种新的GEK模型[23],通过建立一系列子GEK模型来代替原有GEK模型,从而大幅度降低相关矩阵的维度,提高GEK建模的效率。宋超等[24]利用梯度信息,选取扰动步长得到初始样本点附近的派生点,以派生点拟合出能够预测目标函数趋势的低精度Kriging模型。然后以初始样本点修正该模型得到高精度的Kriging模型。显然,该方法并未直接将梯度信息耦合进Kriging建模过程中。

目前,GEK模型已在气动优化设计中得到一些初步应用。Chung[25]和Xuan[26]等将GEK模型与序列二次规划(SQP)法相结合,进行了初步气动优化设计,他们用有限差分法来计算目标函数的梯度,但未对优化效率及优化效果进行研究。刘俊等[27]进行了基于Kriging模型和GEK模型的翼型气动反设计比较研究,使用Adjoint方法计算梯度,发现在计算量一致的前提下,GEK模型优化结果更好且收敛更快。对于设计变量较多(大于30个)的优化问题,Kriging模型的“维度之咒”逐渐凸显。GEK模型能否在一定程度上缓解“维度之咒”,在设计变量个数上有所突破,这成了当前代理优化算法在气动优化应用中鲜有涉及却十分重要的研究方向。另外,由于GEK模型每次建模过程中用到的响应值和梯度值远远多于梯度算法每次寻优过程所用到的响应值和梯度值,所以有必要将基于GEK模型的代理优化算法和改进拟牛顿(BFGS)方法进行比较研究。

本文使用GEK代理优化算法进行了翼型及机翼的压力分布反设计,包括18维翼型气动反设计和36维、108维机翼气动反设计,并和Kriging代理优化方法、BFGS方法进行了对比研究。通过在设计空间局部建立GEK模型,使得基于代理优化算法的气动反设计的维度突破了100维,“维度之咒”得到明显缓解。

1 优化设计方法

1.1 几何参数化与设计变量范围确定

在利用优化方法进行翼型优化设计之前先要用一些设计参数来代替翼型,即对翼型进行参数化。CST参数化方法是由波音公司的工程师Kulfan提出来的。该方法用一个类函数C(¯x)和一个型函数S¯()x 的乘积加上一个描述后缘厚度的函数Δyte来表示一个翼型的几何形状:

关于CST参数化求解方法,具体可参见文献[28]。

同时,还要给定优化过程中设计参数的变化范围。利用一个较“厚”的翼型和一个较“薄”的翼型,并使得这两个翼型之间的范围足够大,可以包含目标翼型。将两个翼型之间的空间作为真实设计空间,如图1中阴影部分所示,c为翼型弦长。两个翼型所对应的CST参数即为设计变量上下限。机翼反设计采用控制剖面翼型的CST参数作为设计变量。

1.2 优化问题数学模型

气动反设计问题转化为优化设计问题后,目标函数可以写为

式中:pd为目标压力分布;p为反设计得到的压力分布;B为沿物面积分;S为积分面。

1.3 试验设计方法

在构建Kriging模型之前,需要采用试验设计方法对设计空间进行抽样,来生成一定数量的初始样本点。

1.3.1 拉丁超立方试验设计

翼型反设计中一般初始样本点个数大于设计变量个数,采用拉丁超立方抽样[29](Latin Hypercube Sampling,LHS)试验设计方法生成初始样本点。它的基本原理为:如果进行ns次抽样(即总共ns个样本点),那么就把nv个设计变量都分成等概率的ns个区间,于是整个抽样空间就被分为等概率的(nv)ns个小区间。然后将ns个样本{0,1,…,ns-1}随机地放入设计空间中并满足下列两个条件:

1)每一个样本点在小区间内随机地分布。

2)将所有样本点投影到任意一维时,每一个小区间内有且仅有一个样本点。

1.3.2 蒙特卡罗试验设计

当初始样本点数小于设计变量个数时,很多试验设计方法已经无法实现而蒙特卡罗(Monte Carlo,MC)抽样[30]仍然适用。机翼反设计中由于设计变量个数较多,初始样本点个数一般少于设计变量个数,所以采用蒙特卡罗抽样试验设计方法生成初始样本点。其实现比较简单,假设给定区间[xl, xu],xu和xl为上下限,在该区间内生成一个随机数,该随机数即所生成的样本点。对于nv维空间,即设计变量为nv,在每一维空间内生成一个随机数,这nv个随机数即构成了设计空间内的一个样本点。

1.4 梯度增强型Kriging模型

本文不对Kriging模型进行详细介绍,详见文献[31-33]。GEK模型是在Kriging模型基础上发展起来的,其思想、原理和建模方法与Kriging模型基本一致。但是GEK模型不仅利用了样本点处的函数值,还利用了样本点处的梯度值。下面介绍本文所采用的由Han等[22]发展的一种直接GEK模型。

首先,在Kriging模型中,对于m维问题,假设对目标函数(或状态变量)抽样获得n个函数值,抽样位置及相应的样本点响应值可写成

式中:S为样本矩阵,每一行代表一个样本点;ys为列向量,每一个元素代表一个样本点的函数值。建立近似模型的目的就是利用已知的样本数据(S,ys),来获得任意未知点处的预测值。

对于GEK模型,将上述样本数据的响应值列向量加以拓展,把样本点处的梯度信息以偏导数的形式加入到响应值中。于是得到含梯度信息的样本及响应值矩阵为式中:xg(j)(j∈{1,2,…,n′})为第j个提供偏导数的样本点(每个偏导数看作一个样本点);向量ys∂y(j)中的∂y(j)= (∂x)表示第j个偏导数信息(对

k第k个独立变量的偏导数,k∈ {1,2,…,m})。

需要说明的是,这里梯度信息的引入具有一般性:梯度信息的抽样位置可以与函数值的抽样位置相同,也可不同;可以引入所有偏导数信息,也可只引入部分偏导数信息。也就是说,总的偏导数个数n′可以小于n·m。如果没有任何偏导数信息,GEK模型将退化为传统的Kriging模型。因此,可以认为,这种GEK模型是一种可考虑梯度信息的更一般化的Kriging模型。

随着优化设计问题维度的增加,如果在优化过程中采用所有的样本点进行GEK建模,模型训练过程将面临非常巨大的计算量(对于108维气动反设计算例,每个样本点都有1个响应值和108个梯度值,以100个样本点为例,GEK模型需构建的相关矩阵大小将是10 900×10 900)。在本文的108维算例中,将反设计问题作为局部优化问题处理,GEK模型每次建模只使用当前所有样本点中距离当前最优点最近的10个样本点,这样每次建立局部代理模型时相关矩阵的大小都可以控制为1 090×1 090,大幅减小了优化建模部分的计算量。事实证明这种方法在高维机翼气动反设计中是高效可行的。

1.4.1 GEK预测值与均方误差

GEK模型对未知函数的预测值定义为所有抽样函数值和所有抽样偏导数值的加权,即

式中:w(i)为第i个函数值的加权系数;λ(j)为第j个偏导数信息的加权系数。与Kriging模型类似,引入静态随机过程假设:

式中:β0∈1为未知常数;Z(·)为均值为0的静态随机过程,且协方差满足

式中:σ2为随机过程Z(·)的方差;R为仅与空间距 离 有 关 的 “相 关 函 数 ”;和分别为相关函数相对于x(i)和x(j)处第k个分量的偏导数。

与Kriging模型推导过程类似,可得到GEK模型的预测值为

式中:R为样本点相关矩阵;r为样本点与未知点x的相关向量;F=[1 … 1 0 … 0]T;β0=(FTR-1F)-1FTR-1ys。

均方误差MSE为

1.4.2 相关函数模型

相关矩阵R和相关向量r的建立需要计算相关函数及其一阶导数、二阶导数值。假设两个样本点x(i)和x(j)之间的相关函数仅与两点之间的距离有关(即R(x(i),x(j))=R(x(i)-x(j))),于是,此处考虑以下形式的相关模型:

本文采用3次样条相关函数:

1.4.3 参数模型

由式(10)可知,GEK模型中存在超参数θ,

与Kriging模型相同,该超参数通过采用最大似然估计(MLE)法求解下列优化问题获得

1.5 加点准则及其约束处理

代理优化方法的一个关键技术是加点准则。由于建立一个较精确的全局近似模型需要大量的样本点,特别是设计变量较多时,因此,为了减少总的样本点数,首先使用较少的样本点建立初始代理模型,再寻找一定准则下的最优点并将其作为新的样本点来更新代理模型重新优化。加点准则的使用直接决定了优化的成败及优化效率。

本文的气动反设计优化算例中,加点方法采用MSP(Minimum of Surrogate Prediction)[34]准则。该准则认为代理模型足够精确,直接寻找代理模型上目标函数的最小值,即建立代理模型后,求解下列子优化问题:

式中:NG为约束个数;^y(x)和^gi(x) 分别为目标函数和约束函数的代理模型。本文使用遗传算法和梯度优化相结合的方法求解式(13)子优化问题,可得到代理模型上预测的目标函数最优解x*。再对x*进行精确数值模拟分析,并将结果作为新的样本数据,添加到现有样本数据集中,重新建立代理模型,直至整个优化过程收敛。该准则是一种局部加点准则,在气动反设计问题中有较好的效果。

1.6 优化设计流程

本文气动反设计优化采用自主开发的优化软件SurroOpt,是结合代理模型、试验设计方法、多点加点准则、遗传算法、梯度优化算法等发展的代理优化设计方法。图2给出了代理模型优化设计方法的流程图,图中DoE(Design of Experiment)表示试验设计。

2 流场求解程序验证

采用自主开发的二维和三维流场求解程序PMNS2D/3D,通过求解雷诺平均Navier-Stokes方程对翼型及机翼进行气动分析。空间离散采用中心有限体积法,LU-SGS隐式时间推进,使用了隐式残值光顺、当地时间步长、多重网格等加速收敛措施。

2.1 RAE2822翼型绕流计算

翼型为RAE2822亚临界翼型,计算网格如图3所示。全湍流计算,湍流模型为剪切应力输运(SST)模型,计算状态为马赫数Ma=0.72,迎角α=2.8°,雷诺数Re=6.5×106。根据图4可以看出:计算压力系数Cp分布与试验值吻合较好,验证了二维流场求解程序的可靠性。

2.2 M6机翼绕流计算

M6机翼的表面网格和空间网格如图5所示,网格量为50万。全湍流计算,采用Spalart-Allmaras湍流模型,计算状态为Ma=0.839 5,α=3.06°,Re=1.17×107。由图6可以看出,M6机翼不同站位的压力分布计算值与试验值吻合较好,验证了三维流场求解程序的可靠性。图中:z/b表示机翼展向位置坐标与半展长的比值。

3 Adjoint梯度求解程序验证

采用自主开发的二维和三维梯度求解程序,通过求解连续Adjoint方程得到反设计目标函数对所有设计变量的梯度。并和二阶精度有限差分方法计算的梯度进行比较,来验证Adjoint梯度求解程序的可靠性。

3.1 RAE2822翼型压力分布反设计梯度

目标压力分布为RAE2822翼型在计算状态下的压力分布。计算翼型为NACA0012翼型,计算网格的类型和规模与图3所示的网格一致。计算状态为 Ma=0.72,α=2.8°,Re=6.5×106。根据图7可以看出2种方法计算的梯度值吻合较好,验证了二维Adjoint梯度求解程序的可靠性。

3.2 M6机翼压力分布反设计梯度

目标压力分布为M6机翼在计算状态下的表面压力分布。计算机翼的翼根和翼梢剖面形状均为NACA0012翼型,计算网格的类型和规模与图5所示网格一致。计算状态为Ma=0.839 5,α=3.06°,Re=1.17×107。根据图8可以看出2种方法计算的梯度值吻合较好,验证了三维Adjoint梯度求解程序的可靠性。

4 反设计算例与分析

使用基于GEK模型的代理优化方法进行了18、36、108维的气动反设计研究,同时和Kriging代理优化设计方法及BFGS方法进行了对比。需要说明的是,GEK模型建模和BFGS方法所需要的梯度信息均采用Adjoint方法求解,用Adjoint方法求解一次反设计目标函数对所有设计变量的梯度,花费的计算量相当于一次CFD求解。对于三维外形,CFD分析的计算量远大于代理模型建模的计算量,所以仅以CFD分析次数作为计算量统计的依据。

4.1 RAE2822翼型18维反设计

以RAE2822翼型单目标反设计为例。设计状态为Ma=0.734,α=2.79°,Re=6.5×106。在求解Navier-Stokes方程时,采用SST湍流模型进行全湍流计算。

使用8阶CST参数化方法,共18个设计变量。使用基于GEK模型的代理优化方法开展了RAE2822翼型气动反设计,并和Kriging代理优化方法及BFGS方法进行了对比研究。取相同的设计空间,代理优化方法取20个初始样本点,加点准则为MSP。

根据表1展示的优化设计结果可以看出,GEK代理优化方法的效率是Kriging代理优化方法的3倍,最终得到的目标函数值是Kriging代理优化方法的1/5。GEK代理优化方法的效率是BFGS的2.5倍,最终得到的目标函数值略小于BFGS方法。

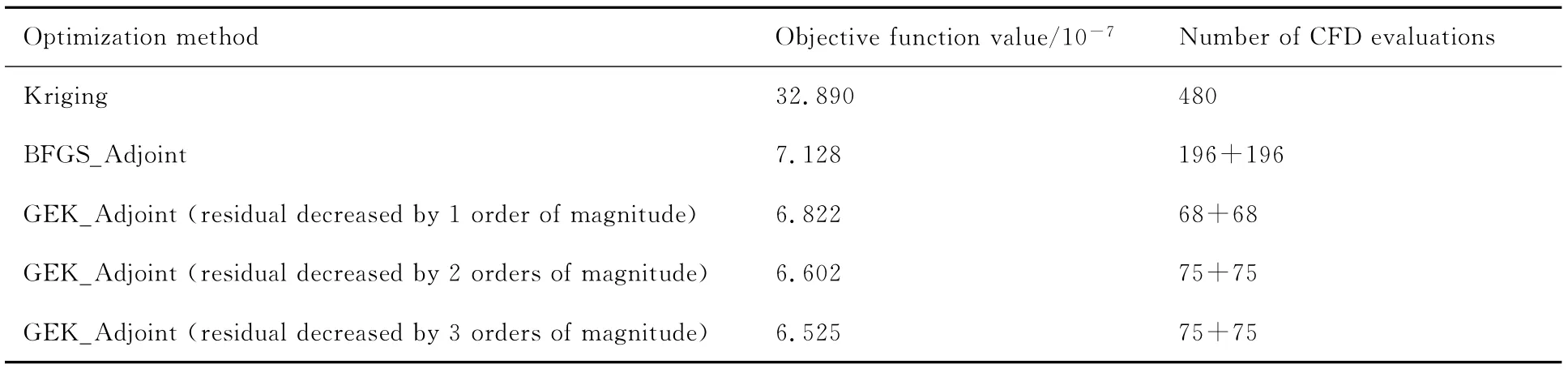
表1 RAE2822翼型反设计结果Table 1 Inverse design results of RAE2822 airfoil

根据图9所示的目标函数收敛历程,可以看出相比Kriging模型,GEK模型使得翼型代理优化的效率大幅提高。说明梯度信息可以提高代理模型精度,从而使用更少的样本点即可锁定最优点的位置。本算例中,相对于BFGS方法,GEK代理优化方法也具有较明显的效率优势,最终优化效果也更好。

根据图10(a)和图10(b)可以看出,使用3种优化方法的反设计翼型外形及压力分布与目标翼型及压力分布吻合较好,说明3种方法都达到了较好的反设计效果。

通过控制连续Adjoint方程求解残差的下降量级,可以间接控制Adjoint梯度的求解精度。分别将Adjoint求解残差下降1、2、3个量级的梯度用于基于GEK模型的代理优化。从表1的优化结果和图11给出的优化收敛曲线可以看出,GEK模型所使用的梯度精度越高,最终的反设计目标函数越小,反设计效果越好,同时计算量相当。

4.2 M6机翼36维反设计

以M6机翼单目标反设计为例。设计状态为Ma=0.839 5,α=3.06°,Re=1.17×107。

剖面翼型使用8阶CST参数化方法,翼根翼梢两个剖面共36个设计变量,通过两个剖面沿展向线性插值即可得到M6机翼。使用基于GEK模型的代理优化方法开展了M6机翼气动反设计优化,并和Kriging代理优化方法及BFGS方法进行了对比研究。取相同的设计空间,代理优化方法取10个初始样本点,加点准则为MSP。

根据表2展示的优化设计结果可以看出,基于Kriging模型的代理优化方法花费了将近8倍于GEK模型的计算量,最终得到的目标函数是GEK模型的2.5倍。GEK代理优化方法的优化效果略优于BFGS方法,但BFGS调用的流场求解次数是GEK代理优化方法的2.6倍。

根据图12所示的目标函数收敛历程,可以看出在36维的气动反设计问题中,Kriging模型的“维度之咒”已经开始显现。此时采用GEK模型可以使机翼反设计的效率大幅度提高。

表2 M6机翼反设计结果Table 2 Inverse design results of M6 wing

图13(a)和图13(b)给出了反设计机翼和M6机翼的19%站位剖面翼型的外形及压力分布比较。图14(a)和图14(b)给出了反设计机翼和M6机翼的79%站位剖面翼型的外形及压力分布比较。可以看出使用3种方法的反设计机翼外形及压力分布与目标机翼及压力分布均吻合较好。

根据图15所示的目标函数收敛历程可以看出,GEK模型所使用的梯度精度越高,最终目标函数越小,反设计效果越好。

4.3 CRM机翼108维反设计

对第五届AIAA阻力预测研讨会(DPW-5)所使用的由NASA开发的CRM机翼进行气动反设计(Ma=0.85,α=2.16°,Re=5.0×106)。

CRM机翼平面形状比较复杂,以图16所示的9个剖面翼型形状参数作为设计变量进行压力分布反设计。将9个剖面沿展向样条插值后即可近似得到CRM机翼。采用5阶CST参数化方法,对剖面翼型进行参数化,每个剖面有12个设计变量,9个剖面共108个设计变量。

CRM机翼绕流计算使用的网格为C-H结构化网格,如图17所示。网格量约140万,远场约为翼根弦长的30倍。

如前文所述,为了减少高维问题中GEK模型训练所花费的时间,在设计空间局部建立GEK模型来进行CRM机翼气动反设计,并和Kriging代理优化方法及BFGS方法进行对比研究。取相同的设计空间,代理优化取100个初始样本点,使用MSP加点准则。

根据表3给出的CRM机翼代理气动反设计结果可以看出,使用GEK模型最终得到的目标函数大小约为Kriging模型的1/65,而花费的计算量不到Kriging模型的1/2。预计在本算例中,要达到相当的优化效果,基于Kriging模型的代理优化方法花费的计算量将是基于GEK模型的代理优化方法的数十倍。同时,在108维反设计算例中,GEK代理优化方法的优化效果略优于BFGS方法,流场求解的调用次数也略少于BFGS方法。需要说明的是,在本算例当中,由于只在设计空间局部建立GEK模型,GEK代理优化算法的优势可能没有得到充分发挥。

图18给出了不同方法反设计收敛曲线的比较,图19～图21分别给出了反设计机翼0.5%站位(翼根)、40.8%站位及99.4%站位(翼梢)处的剖面翼型及压力分布和CRM机翼的比较。可以看出,基于GEK模型的代理优化方法使用不到500次CFD计算得到的外形和CRM机翼吻合得很好,而基于Kriging模型的代理优化方法花费了1 000次CFD计算,得到的外形和CRM机翼仍有较明显的差距。

5 结 论

1)对于翼型和机翼的气动反设计,基于GEK模型的代理优化方法比基于Kriging模型的代理优化方法具有明显的效率优势。相比于BFGS方法,基于GEK模型的代理优化方法仍然有更高的效率,同时也可以得到更好的优化效果。

2)Adjoint梯度求解精度越高,基于GEK模型的代理气动反设计效果越好。

3)对大于30个设计变量的高维优化问题,基于Kriging模型的代理优化开始显现“维度之咒”。GEK模型由于在建模过程中使用了梯度信息,可以使用较少的样本点来建立高精度的模型,在高维问题中表现出了巨大的效率优势。基于GEK模型的代理优化方法可在一定程度上缓解“维度之咒”,使得代理优化问题的维度成功拓展到100维以上。

本文所采用的GEK模型,在设计变量和样本点数量较多的情况下,建模所花费的时间仍然较多,所以在108维算例中采用了建立局部代理模型的方法来减少计算成本。今后需要对该模型做进一步改进,提高模型训练效率,在高维问题中利用所有样本点的响应值和梯度值来建立高精度代理模型,从而更加充分地发挥GEK模型的优势。

致 谢

感谢刘俊博士在优化设计平台开发方面所做的工作。

[1] 韩忠华.Kriging模型及代理优化算法研究新进展[J].航空学报,2016,37(11):3197-3225.HAN Z H.Kriging surrogate model and its application to design optimization:A review of recent progress[J].Acta Aeronautica et Astronautica Sinica,2016,37(11):3197-3225(in Chinese).

[2] HAN Z H.SurroOpt:A generic surrogate-based optimization code for aerodynamic and multidisciplinary design[C]//30th Congress of the International Council of the Aeronautical Aciences,2016.

[3] 王晓锋,席光.基于Kriging模型的翼型气动性能优化设计[J].航空学报,2005,26(5):545-549.WANG X F,XI G.Aerodynamic optimization design for airfoil based on Kriging model[J].Acta Aeronautica et Astronautica Sinica,2005,26(5):545-549(in Chinese).

[4] 许瑞飞,宋文萍,韩忠华.改进Kriging模型在翼型气动优化设计中的应用研究[J].西北工业大学学报,2010,28(4):503-510.XU R F,SONG W P,HAN Z H.Application of improved Kriging-model-based optimization method in airfoil aerodynamic design[J].Journal of Northwestern Polytechnical University,2010,28(4):503-510(in Chinese).

[5] 白俊强,王波,孙智伟,等.基于松散式代理模型管理框架的亚音速机翼优化设计方法研究[J].西北工业大学学报,2011,29(4):515-519.BAI J Q,WANG B,SUN Z W,et al.Developing optimization design of subsonic wing with losse type of agent model[J].Journal of Northwestern Polytechnical University,2011,29(4):515-519(in Chinese).

[6] 张科施,韩忠华,李为吉,等.基于近似技术的高亚声速运输机机翼气动/结构优化设计[J].航空学报,2006,27(5):810-815.ZHANG K S,HAN Z H,LI W J,et al.Multidisciplinary aerodynamic/structural design optimization for high subsonic transport wing using approximation technique[J].Acta Aeronautica et Astronautica Sinica,2006,27(5):810-815(in Chinese).

[7] 姚拴宝,郭迪龙,孙振旭,等.基于Kriging代理模型的高速列车头型多目标优化设计[J].中国科学:技术科学,2013,43(2):186-200.YAO S B,GUO D L,SUN Z X,et al.Multi-objective optimization of the streamlined head of high-speed trains based on the Kriging model[J].Scientia Sinica:Techchnologica,2013,43(2):186-200(in Chinese).

[8] LIU J,SONG W P,HAN Z H,et al.Efficient aerodynamic shape optimization of transonic wings using a parallel infilling strategy and surrogate models[J].Structural&Multidisciplinary Optimization,2016:1-19.

[9] KIM H J,RHO O H.Aerodynamic design of transonic wings using the target pressure optimization approach[J].Journal of Aircraft,1998,35(5):671-677.

[10] 赵国庆,招启军.基于目标压力分布的旋翼先进气动外形反设计分析方法[J].航空学报,2014,35(3):744-755.ZHAO G Q,ZHAO Q J.Inverse design analysis method on rotor with advanced aerodynamic configuration based upon target pressure distribution[J].Acta Aeronautica et Astronautica Sinica,2014,35(3):744-755(in Chinese).

[11] TOAL D J J,BRESSLOFF N W,KEANE A J.Kriging hyperparameter tuning strategies[J].AIAA Journal,2008,46(5):1240-1252.

[12] TOAL D J J,BRESSLOFF N W,KEANE A J,et al.The development of a hybridized particle swarm for kriging hyperparameter tuning[J].Engineering Optimization,2011,43(6):675-699.

[13] 刘俊,宋文萍,韩忠华,等.Kriging模型在翼型反设计中的应用研究[J].空气动力学学报,2014,32(4):518-526.LIU J,SONG W P,HAN Z H,et al.Kriging-based airfoil inverse design[J].Acta Aerodynamica Sinica,2014,32(4):518-526(in Chinese).

[14] SHAN S.Survey of modeling and optimization strategies for high-dimensional design problems[J].Chemical Engineering Science,2015,141(2):184-194.

[15] JAMESON A,REUTHER J.Control theory based airfoil design using the Euler equations[C]//5th Symposium on Multidisciplinary Analysis and Optimization.Reston:AIAA,1994.

[16] JAMESON A.Aerodynamic design via control theory[J].Journal of Scientific Computing,1988,3(3):233-260.

[17] JAMESON A.Optimum aerodynamic design using CFD and control theory:AIAA-1995-1729[R].Reston:AIAA,1995.

[18] LIU W Y,BATILL S M.Gradient-enhanced response surface approximations using kriging models[C]//9th AIAA/ISSMO Symposium and Exhibit on Multidisciplinary Analysis and Optimization.Reston:AIAA,2002.

[19] CHUNG H S,ALONSO J J.Using gradients to construct cokriging approximation models for high-dimensional design optimization problems:AIAA-2002-0317[R].Reston:AIAA,2002.

[20] LAURENCEAU J,SAGAUT P.Building efficient response surfaces of aerodynamic functions with kriging and cokriging[J].AIAA Journal,2008,46(2):498-507.

[21] LAURENCEAU J,MEAUX M,MONTAGNAC M,et al.Comparison of gradient-based and gradient-enhanced response-surface-based optimizers[J].AIAA Journal,2010,48(5):981-994.

[22] HAN Z H,GÖRTZ S,ZIMMERMANN R.Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function[J].Aerospace Science and Technology,2013,25(1):177-189.

[23] HAN Z H,SONG C X,ZHANG Y.A new formulation of gradient-enhanced surrogate model and application to aerodynamic design[C]//34th AIAA Applied Aerodynamics Conference.Reston:AIAA,2016.

[24] 宋超,杨旭东,宋文萍.耦合梯度与分级Kriging模型的高效气动优化方法[J].航空学报,2016,37(7):2144-2155.SONG C,YANG X D,SONG W P.Efficient aerodynamic optimization method using hierarchical Kriging combined with gradient[J].Acta Aeronautica et Astronautica Sinica,2016,37(7):2144-2155(in Chinese).

[25] CHUNG H S,ALONSO J J.Design of a low-boom supersonic business jet using cokriging approximation models:AIAA-2002-5598[R].Reston:AIAA,2002.

[26] XUAN Y,XIANG J H,ZHANG W H,et al.Gradientbased Kriging approximate model and its application research to optimization design[J].Science in China Series E:Technological Sciences,2009,52(4):1117-1124.

[27] 刘俊,宋文萍,韩忠华,等.梯度增强的Kriging模型与Kriging模型在优化设计中的比较研究[J].西北工业大学学报,2015,33(5):819-826.LIU J,SONG W P,HAN Z H,et al.Comparative study of GEK(Gradient-Enhanced Kriging)and Kriging when applied to design optimization[J].Journal of Northwestern Polytechnical University,2015,33(5):819-826(in Chinese).

[28] KULFAN B M.Universal parametric geometry representation method[J].Journal of Aircraft,2008,45(1):142-158.

[29] GIUNTA A A,WOJTKIEWICZ S F,ELDRED M S.Overview of modern design of experiments methods for computational simulations[C]//Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit.Reston:AIAA,2003.

[30] METROPOLIS N,ULAM S.The Monte Carlo method[J].Journal of the American Statistical Association,1949,44(247):335-341.

[31] HOYLE N,BRESSLOFF N W,KEANE A J.Design optimization of a two-dimensional subsonic engine air intake[J].AIAA Journal,2006,44(11):2672-2681.

[32] HAN Z H,ZHANG K S,SONG W P,et al.Optimization of active flow control over an airfoil using a surrogatemanagement framework[J].Journal of Aircraft,2010,47(2):603-612.

[33] HAN Z H,ZHANG K S,LIU J,et al.Surrogate-based aerodynamic shape optimization with application to wind turbine airfoils:AIAA-2013-1108[R].Reston:AIAA,2013.

[34] LIU J,HAN Z H,SONG W P.Comparison of infill sampling criteria in Kriging-based aerodynamic optimization[C]//28th International Congress of the Aeronautical Sciences,2012.

Aerodynamic inverse design method based on gradient-enhanced Kriging model

HAN Shaoqiang,SONG Wenping,HAN Zhonghua*,WANG Le

National Key Laboratory of Science and Technology on Aerodynamic Design and Research,School of Aeronautics,Northwestern Polytechnical University,Xi'an 710072,China

Up to date,the surrogate-based optimization methods using Kriging model are widely used in the aerodynamic optimization design.However,the huge time costs seriously restrict the in-depth development of Kriging model when it comes to cases with dimension course(more than 30 design variables).lnverse design problems of airfoils and wings are formulated as optimization problems.Surrogate-based optimization using gradient-enhanced Kriging(GEK)model is adopted to conduct aerodynamic inverse design of 18,36 and 108 variables,and gradient is solved via the efficient adjoint method.lt is worth mentioning that the dimension of aerodynamic inverse design using surrogate-based optimization is successfully expanded to more than 100 by constructing GEK model in part of the design space.Besides,the influence of gradient accuracy on surrogate-based optimization using GEK model is studied.The results show that the effect of optimization is improved with more accurate gradients.BFGS(Broyden,Fletcher,Goldfarb and Shanno)and surrogate-based optimizations using GEK and Kriging models are compared through aerodynamic inverse design of different dimensions.The results show that surrogate-based optimization using GEK model has significantly higher efficiency,and the advantage of efficiency is more obvious with higher dimension of design.At the same time,surrogate-based optimization using GEK model has better optimization effect and less number of calls of analysis programs than the BFGS method.

design optimization;Kriging;gradient-enhanced Kriging(GEK);surrogate model;BFGS;inverse design of airfoil;inverse design of wing

2016-09-26;Revised:2016-10-17;Accepted:2016-11-15;Published online:2016-11-24 10:34

URL:www.cnki.net/kcms/detail/11.1929.V.20161124.1034.006.html

National Natural Science Foundation of China(11272265)

V211.3

A

1000-6893(2017)07-120817-15

10.7527/S1000-6893.2016.0299

2016-09-26;退修日期:2016-10-17;录用日期:2016-11-15;网络出版时间:2016-11-24 10:34

www.cnki.net/kcms/detail/11.1929.V.20161124.1034.006.html

国家自然科学基金(11272265)

*通讯作者.E-mail:hanzh@nwpu.edu.cn

韩少强,宋文萍,韩忠华,等.基于梯度增强型Kriging模型的气动反设计方法[J].航空学报,2017,38(7):120817.HAN S Q,SONG W P,HAN Z H,et al.Aerodynamic inverse design method based on gradient-enhanced Kriging model[J].Acta Aeronautica et Astronautica Sinica,2017,38(7):120817.

(责任编辑:李明敏)

*Corresponding author.E-mail:hanzh@nwpu.edu.cn