基于稀疏表示和近似0范数约束的宽带信号DOA估计

燕学智， 温艳鑫， 刘国红， 陈建

吉林大学 通信工程学院， 长春 130022

燕学智， 温艳鑫， 刘国红*， 陈建

吉林大学 通信工程学院， 长春 130022

针对宽带信号的波达方向(DOA)估计问题，在稀疏框架下提出一种近似0范数约束的宽带信号DOA估计新算法。首先对宽带信号进行预处理，得到同一参考频率点下的接收数据，然后对其协方差矩阵元素进行加和平均运算，得到一个低维的观测向量，并在稀疏框架下进行稀疏表示，最后利用截断1函数设定权值，构造逼近0范数约束的稀疏重构方法，进而重构信号，获得宽带信号的DOA估计。仿真结果表明，相比于传统的宽带信号DOA估计算法，所提算法具有更高的分辨率和估计精度。

信号处理； 宽带信号； 稀疏重构； DOA估计；0范数

近年来，信息技术飞速发展，人们对信息的传播速度及信息容量的要求也越来越严格。宽带信号因其携带信息量大、抗干扰能力强等优点，得到越来越多的重视。作为宽带通信技术领域的一项重要内容，宽带信号波达方向(DOA)估计技术已成为阵列信号处理领域的热点研究问题之一[1-4]。

目前，宽带信号的高分辨率DOA估计方法主要有两类：基于非相干信号的处理方法(Incoherent Signals-subspace Method， ISM)[5]和基于相干信号的处理方法(Coherent Signals-subspace Method， CSM)[6]。ISM[5]的主体思想是把宽带信号分解为不同频率的若干窄带信号，然后对每一个窄带信号进行处理，最后对所有窄带信号的数据进行融合，得到宽带信号的DOA估计。该算法处理过程简单，能较好地处理宽带非相干信号，但未能综合利用宽带信息，计算复杂度较高。Wang和Kaveh在1985年提出了CSM[6]，利用聚焦变换的思想，将不同频率点下的窄带数据变换到同一参考频率点下，消除各窄带数据之间的相关性，然后运用ISM进行DOA估计。该算法分辨率较高，但在信噪比较低、快拍数有限或信源空间间隔小的情况下估计效果不佳。

阵列接收信号的空域稀疏性为信源的DOA估计问题提供了新思路，即在稀疏重构的框架下估计信源入射角度。近年来，稀疏重构方法已广泛应用于窄带DOA估计[7-11]，并已扩展至宽带信号[12-14]。其中，具有代表性的1-SVD算法[9]是对接收数据进行奇异值分解，得到信号子空间，并利用二阶锥归化求解优化问题。但该算法计算复杂度高，且未综合考虑宽带信号各子频数据的联合稀疏性，在此基础上，文献[12-13]提出了宽带1-SVD算法的拓展算法，实现了宽带信号的联合稀疏重构，降低了计算复杂度，但在重构过程中，所选惩罚函数的约束不公平，对大系数惩罚重于小系数，导致有偏估计，影响估计精度。

1 宽带信号模型

考虑一个由M个阵元组成的均匀线阵，P个不相关的宽带信号以不同的方位角θp(p=1,2,…,P)入射到阵列，假设各信源在相同的频带区间[fL,fH]上，则第m个阵元的接收数据可表示为

(1)

式中：sp(t)为第p个信源；dm为第m个阵元到参考阵元的距离；c为信号的传播速度；θp为第p个待估计的信源角度；nm(t)为第m个阵元上均值为零、方差为σ2且与各信源互不相关的噪声数据。

在时域建立宽带信号处理模型较为困难，考虑从频域建立，将观测时间内的接收数据等分为W个子段，然后对每个子段数据进行K点快速傅里叶变换(FFT)变换，则阵列接收数据可以表示成K个不同中心频率的窄带数据，每个窄带信号的采样点数为W，即

X(fk)=A(fk,θ)S(fk)+N(fk)k=1,2,…,K

(2)

式中：X(fk)=[X1(fk)X2(fk) …XM(fk)]T，S(fk)=[S1(fk)S2(fk) …SP(fk)]T，fL≤fk≤fH，分别为M×W维和P×W维的矩阵；A(fk,θ)为M×P维的方向矩阵，其表达式为

A(fk,θ)=

[a(fk,θ1)a(fk,θ2) …a(fk,θP)]

其中：A(fk,θ)的列矢量为M×1的导向量，θ=[θ1θ2…θP]。A(fk,θ)中第p个信源的阵列流型为

a(fk,θp)=

[1 e-j2πfkd1sin θp/c… e-j2πfkdM-1sin θp/c]T

由此可见，宽带信号模型本质上是对阵列接收信号进行频域采样，得到对应于不同频率的一系列窄带数据。

2 DOA估计

基于相干信号的处理方法，其主要思想是将宽带数据分解为频率不同的若干子带数据，然后把各个频率点的数据通过聚焦变换，转换成同一频率点下的数据，最后运用ISM进行DOA估计。该方法的不足是，在快拍数少、信噪比较低或信源空间间隔较小时，不能准确估计出信源入射角度。而基于稀疏重构的宽带1-SVD算法及其拓展算法在稀疏重构过程中，所选惩罚函数约束不公平，会导致有偏估计。针对上述问题，本文提出一种新的基于稀疏重构的宽带信号DOA估计算法，对宽带数据进行预处理及聚焦变换后，对得到的协方差矩阵元素进行加和平均运算，得到集中噪声能量的低维观测向量，在稀疏框架下进行稀疏表示，并利用TLP惩罚函数构建加权系数，增强信号稀疏性，逼近0范数重构信号，获得更好的估计精度与角度分辨率。

2.1 观测模型的建立

假设第k个窄带数据的频率fk对应的变换矩阵为T(fk)，则通过对X(fk)作聚焦变换，可得到变换后的数据Y(fk)为

Y(fk)=T(fk)X(fk)=

T(fk)A(fk,θ)S(fk)+T(fk)N(fk)=

A(fc,θ)S(fk)+T(fk)N(fk)

(3)

聚焦后相关数据的协方差矩阵为

(4)

式中：

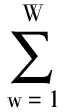
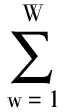
令

则最终可得

Ry=A(fc,θ)RSAH(fc,θ)+RN

(5)

式中：gk为与信噪比成比例的归一化权值，假设为1；fc为参考频率。变换矩阵T(fk)应满足的条件为

k=1,2,…,K

s.t.T(fk)TH(fk)=I

(6)

式(6)的解不唯一，这里，选择

T(fk)=Q(fc)QH(fk)

(7)

参考频率点的选取十分关键，它的取值应使式(8)的聚焦误差最小：

k=1,2,…,K

s.t.T(fk)TH(fk)=I

(8)

使得式(8)聚焦误差最小的条件为

(9)

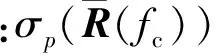
(10)

Ry的展开表达式为[15-16]

(11)

式中：

式中：δ(·)为狄拉克函数；Pp为第p个信源的能量；Y=[Y(f1)Y(f2) …Y(fK)]；可以看出，Ry(m1,m2)=Ry(n1,n2)，m1-m2=n1-n2；m1,m2,n1,n2∈[1,M]。这表现了Ry的特殊性，且只在主对角线上包含噪声能量，从而可以通过加和平均变换得到一个低维的观测向量，令y为一个(2M-1)×1的向量，其第i(1≤i≤2M-1)个元素为

(12)

y的矩阵形式为

y=B(fc,θ)P+σ2I2M-1

(13)

式中：

B(fc,θ)=[b(fc,θ1)b(fc,θ2) …b(fc,θP)]

b(fc,θp)=[ej2πfcdM-1 sin θp/c… 1 …

e-j2πfcdM-1 sin θp/c]T

P=[P1P2…PP]T

I2M-1为(2M-1)×1的向量，它的第M个元素为1，其他均为0，即新模型只在第M个元素上包含噪声，达到了集中噪声能量及降维的目的，提高了重构精度。

2.2 基于稀疏重构的DOA估计

(14)

(15)

(16)

(17)

式中：W(j-1)=diag(w1,w2,…,wQ)为由TLP惩罚函数构造的加权向量，即

(18)

式中：ε为远小于1的数；τ为一个阈值。此时，式(17)可写为

(19)

式(16)～式(19)可以借助凸优化工具包(如SeDuMi[22]，CVX[23])求解。

(20)

式中：Un为Ry的噪声子空间，对应Ry的M-P个小特征值。

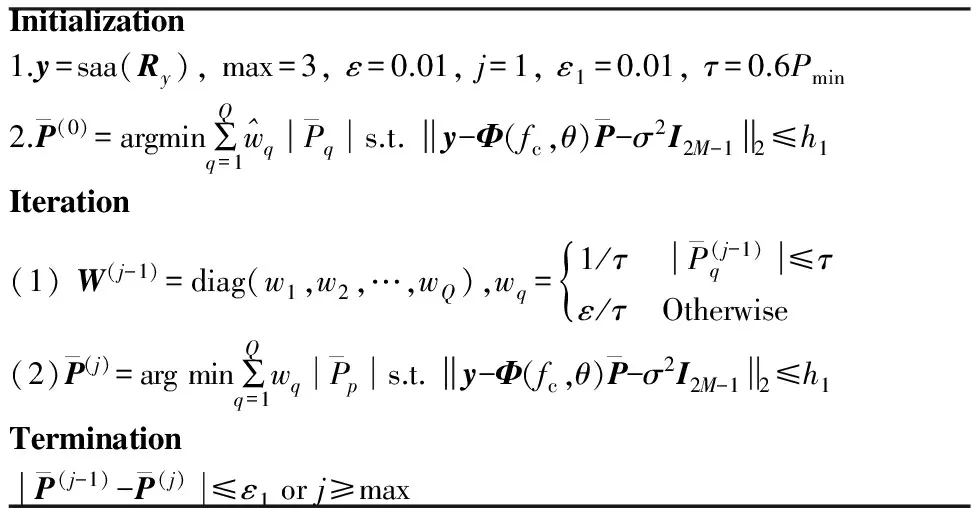
表1 本文所提算法Table 1 The proposed algorithm

3 仿真实验

考虑一个阵元数为M=8的均匀线阵，假设宽带非相关入射信号具有相同的中心频率f0=108Hz和信号带宽Bw=107Hz，相对带宽为10%，阵元间距d=c/2fH。通过窄带叠加法产生宽带信号模型。噪声为零均值的高斯过程，与信号具有相同的带宽且与信号相互独立，采样频率为fs=2fH，信号带宽被分解为K=8个子带。先以1° 间隔对-90°～90° 的空间进行粗网格划分，再在估计出的角度附近作更细化分[24]。

DOA估计的均方根误差(RMSE)通过200次独立的蒙特卡罗仿真实验获得，其定义为

(21)

实验1角度分辨率性能分析

考虑两个空间间隔较小的信源，入射角度分别为15° 和20°，信噪比SNR=10 dB，快拍数L=512，图1为不同算法的空间谱估计结果，可以看出，所提算法有两个明显的谱峰，分别对应仿真条件设定的两个宽带信号的入射角度，能准确分辨出两个信号，角度分辨率较高；而CSM算法估计性能大幅下降，只有一个平缓的谱峰，且谱峰位置偏离信号入射角度，未能准确估计出信源。图2为入射角度为θ1=-10°，θ2=20°，信噪比SNR=-20 dB时不同算法的空间谱，容易看出，CSM算法谱峰十分平缓，较难准确地分辨信号的入射角度，而所提算法在低信噪比下仍能很好地分辨信号，分辨性能优于其他对比算法。图3(a)为不同算法的角度分辨率随SNR的变化关系，入射角度为θ1=10°，θ2=24°，快拍数L=512。图3(b)为不同算法的角度分辨率随角度间隔的变化关系，第1个信源的入射角度固定为θ1=-10°，第2个信源的入射角度θ2由-9° 以1° 间隔变化到5°，信噪比SNR=10 dB。每个SNR和角度间隔下均进行200次独立的蒙特卡罗实验。可以看出，当信噪比较低或信源空间间隔较小时，CSM算法角度分辨率较低，分辨性能大幅下降，而所提算法仍能以相对高的分辨概率准确估计出信源DOA信息，具有更高的角度分辨率。

实验2角度估计精度性能分析

图1 不同算法的空间谱Fig.1 Space spectrum of different algorithms

图2 SNR=-20 dB时不同算法的空间谱 Fig.2 Space spectrum of different algorithms (SNR=-20 dB)

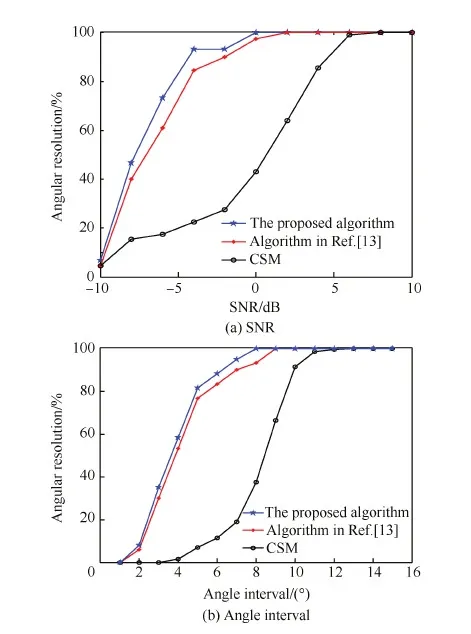
图3 角度分辨率随SNR和角度间隔的变化Fig.3 Angular resolution along with change of SNR and angle interval

考虑入射角度分别为θ1=-30° 和θ2=20°的两个宽带信号，信噪比SNR=10 dB，快拍数L=24，所提算法和CSM算法仿真结果如图4所示，可以看出，所提算法和CSM算法在少快拍数情况下进行DOA估计，所提算法具有较高的估计精度，而CSM算法空间谱较为平缓，几乎无法分辨信源入射角度。

图4 少快拍下不同算法的空间谱 Fig.4 Space spectrum of different algorithms under little snapshots

图5 RMSE随信噪比和快拍数的变化 Fig.5 RMSE along with change of SNR and snapshots

图5(a)为不同算法DOA估计的RMSE随信噪比的变化关系，采样点数固定为L=512，信噪比SNR从-10 dB变化到10 dB。图5(b)为不同算法DOA估计的RMSE随快拍数的变化关系，信噪比固定为SNR=10 dB，快拍数L从128变化到1 024。每个SNR和快拍均进行200次独立的蒙特卡罗实验。可以看出，所提算法的RMSE曲线明显低于CSM算法及文献[13]的算法，说明所提算法在相同的信噪比或快拍数条件下，估计性能优于对比算法，具有更高的估计精度及噪声鲁棒性。

4 结 论

针对宽带信号的DOA估计问题，在稀疏信号重构框架下提出了一种近似0范数约束的宽带信号DOA估计新算法。

1) 算法的重构计算复杂度与宽带信号分频处理时的子频个数无关，可避免在稀疏重构框架下进行宽带信号DOA估计时存在的重构计算量大的问题。

3) 与CSM算法相比，所提算法在低信噪比、小样本或信源空间间隔较小等场合，能够获得均方根误差更小的DOA估计结果，具有更高的角度分辨率和估计精度。

[1] KRIM H, VIBERG M. Two decades of array signal processing research: The parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94.

[2] YADAR A K, SANTOSH S. Comparison of different wideband DOA estimation methods[C]//2015 IEEE International Conference on Computational Intelligence and Computing Research(ICCIC). Piscataway, NJ: IEEE Press, 2015: 1-4.

[3] 邓佳欣, 廖桂生, 杨志伟, 等. 基于虚拟孔径扩展的子带信息融合宽带DOA估计[J]. 系统工程与电子技术, 2016, 38(2): 245-250.

DENG J X, LIAO G S, YANG Z W, et al. Subband information fusion for wideband DOA estimation based on virtual array[J]. System Engineering and Electronics, 2016, 38(2): 245-250 (in Chinese).

[4] 金勇, 黄建国, 张立杰. 宽带信号近似最大似然方位估计快速算法[J]. 航空学报, 2008, 29(5): 1264-1268.

JIN Y, HUANG J G, ZHANG L J. DOA estimation fast algorithm for wideband sources[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1264-1268 (in Chinese).

[5] WAX M, SHAN T J, KAILATH T. Spatio-temporal spectral analysis by eigenstructure methods[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1984, 32(4): 817-827.

[6] WANG H, KAVEH M. Coherent signal-subspace processing for the detection and estimaton of angles of muliple wide-band sources[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(4): 823-831.

[7] CUI W, QIAN T, TIAN J. Enhanced covariances matrix sparse representation method for DOA estimation[J]. Electronics Letters, 2015, 51(16): 1288-1290.

[8] 沈志博, 赵国庆, 董春曦, 等. 基于压缩感知的频率和DOA联合估计算法[J]. 航空学报, 2014, 35(5): 1357-1364.

SHEN Z B, ZHAO G Q, DONG C X, et al. United frequency and DOA estimation algorithm based on compressed sensing[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1357-1364 (in Chinese).

[9] MALIOUTOV D, CETIN M, WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transaction on Signal Processing, 2005, 53(8): 3010-3022.

[10] TIAN Y, SUN X Y, ZHAO S S. Sparse-reconstruction-based direction of arrival, polarisation and power estimation using a cross-dipole array[J]. IET Radar, Sonar & Navigation, 2015, 9(6): 727-731.

[11] HYDER M M, MAHATA K. A robust algorithm for joint sparse recovery[J]. IEEE Signal Processing Letters, 2009, 16(12): 1091-1094.

[12] LIU Z C, WANG X L, ZHAO G H, et al. Wideband DOA estimation based on sparse representation—An extension of1-SVD in wideband cases[C]//IEEE International Conference on Signal Processing, Communication and Computing (ICSPCC). Piscataway, NJ: IEEE Press, 2013: 1-4.

[13] 赵永红, 张林让, 刘楠, 等. 一种新的基于稀疏表示的宽带信号DOA估计方法[J]. 电子与信息学报, 2015, 37(12): 2935-2940.

ZHAO Y H, ZHANG L R, LIU N, et al. A novel method of DOA estimation for wideband signals based on sparse representation[J]. Journal of Electronics & Information Technology, 2015, 37(12): 2935-2940 (in Chinese).

[14] 刘寅, 吴顺君, 吴明宇, 等. 基于空域稀疏性的宽带DOA估计[J]. 航空学报, 2012, 33(11): 2028-2038.

LIU Y, WU S J, WU M Y, et al. Wideband DOA estimation based on spatial sparseness[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2028-2038 (in Chinese).

[15] TIAN Y, SUN X Y, ZHAO S S. DOA and power estimation using a sparse representation of second-order statistics vector and0-norm approximation[J]. Signal Process, 2014, 105: 98-108.

[16] 田野, 孙晓颖, 秦宇镝. 基于两步加权1范数约束的高分辨率波达方向和功率估计[J]. 电子与信息学报, 2014, 36(7): 1637-1641.

TIAN Y, SUN X Y, QIN Y D. High-resolution direction of-arrival and power estimation using two-stage weighted1-norm penalty[J]. Journal of Electronics & Information Technology, 2014, 36(7): 1637-1641 (in Chinese).

[17] CANDES E J, TAO T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203-4215.

[18] CANDES E J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Redus Matematique, 2008, 346(9-10): 589-592.

[19] DONOHO D L, ELAD M, TEMLYAKOV V. Stable recovery of sparse overcomplete representation in the presence of noise[J]. IEEE Transactions on Information Theory, 2006, 52(1): 6-18.

[20] XU X, WEI X, YE Z. DOA estimation based on sparse signal recovery utilizing weighted1-norm penalty[J]. IEEE Signal Processing Letters, 2012, 19(3): 155-158.

[21] FAN J, LI R. Variable selection via nonconcave penalized likelihood and its oracle properties[J]. Journal of American Statistical Association, 2001, 96(456): 1348-1360.

[22] STURM J. Using SeDuMi 1.02, a MATLAB toolox for optimization over svmmetric cones[J]. Optimization Method and Software, 1999, 11(1-4): 625-653.

[23] GRANT M, BOYD S, YE Y. Cvx: Matlab software for disciplined convex programming[EB/OL]. (2008-06-07)[2016-08-26]. http://cvxr.com/cvx.

[24] 陈建, 田野, 孙晓颖. 基于阵列协方差矩阵向量稀疏表示的高分辨波达方向估计[J]. 吉林大学学报: 工学版, 2014, 44(2): 485-489.

CHEN J, TIAN Y, SUN X Y. High resolution direction-of-arrival estimation based on a sparse representation of array covariance matrix column vectors[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(2): 485-489 (in Chinese).

(责任编辑： 苏磊)

Broadband signal DOA estimation based on sparse representationand0-norm approximation

YANXuezhi,WENYanxin,LIUGuohong*,CHENJian

CollegeofCommunicationEngineering,JilinUniversity,Changchun130022,China

Based on0-norm approximation, an efficient algorithm is proposed to deal with the localization of the broadband signal under the sparse framework. First, by preprocessing broadband signal, the

data under the same frequency is obtained. Then a sum-average operation to array covariance matrix elements of the received data is made in order to get a low dimensional observation vector and the sparse representation of the new model under sparse framework is built. Finally, exploiting truncated1function as the weight coefficients to construct0-norm penalty sparse reconstruction method and then reconstruct the broadband signal to obtain DOA estimation. The simulation results demonstrate that comparing to the traditional broadband signal DOA estimate algorithms, the proposed algorithm is able to provide higher resolution and estimation accuracy.

signal processing; broadband signal; sparse reconstruction; DOA estimation;0-norm

2016-08-26；Revised2016-10-08；Accepted2016-12-12；Publishedonline2016-12-211128

URL：www.cnki.net/kcms/detail/11.1929.V.20161221.1128.002.html

s：NationalKeyResearchandDevelopmentProgramofChina(2016YFB1001304)；NationalNaturalScienceFoundationofChina(61171137)

2016-08-26；退修日期2016-10-08；录用日期2016-12-12； < class="emphasis_bold">网络出版时间

时间：2016-12-211128

www.cnki.net/kcms/detail/11.1929.V.20161221.1128.002.html

国家重点研发计划 (2016YFB1001304)； 国家自然科学基金 (61171137)

*

.E-mailliugh10@mails.jlu.edu.cn

燕学智， 温艳鑫， 刘国红， 等． 基于稀疏表示和近似0范数约束的宽带信号DOA估计J． 航空学报,2017,38(6):320705.YANXZ,WENYX,LIUGH,etal.BoardbandsignalDOAestimationbasedonsparserepresentationand0-normapproximationJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):320705.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.320705

V247； TN911.7

A

1000-6893(2017)06-320705-08

*Correspondingauthor.E-mailliugh10@mails.jlu.edu.cn