一种基于短时机动试飞数据的动力学辨识优化方法

王保印， 张曙光,*， 贾晓鹏

1.北京航空航天大学 交通科学与工程学院， 北京 100083 2.中国飞行试验研究院 飞机所， 西安 710089

一种基于短时机动试飞数据的动力学辨识优化方法

王保印1， 张曙光1,*， 贾晓鹏2

1.北京航空航天大学 交通科学与工程学院， 北京 100083 2.中国飞行试验研究院 飞机所， 西安 710089

飞行动力学辨识算法的一个关键问题是，如何通过简单的机动获取所关心频率范围的响应特性。短时倍脉冲是一种易于实施的激励信号，兼顾试飞安全性与经济性，但与频域辨识法通常使用的扫频输入激励相比，短时机动频谱范围窄、信噪比低，一般难以得到准确的辨识结果。对如何基于短时机动飞行试验数据，提高辨识结果准确性的问题进行了研究。首先分析了经典Welch谱估计进行时域-频域转换过程中，影响非参数模型辨识精度的主要因素，提出了削减窗函数边缘缩减效应的数据预处理方法，并结合多窗口综合技术，提高频域特性辨识结果的精度。在参数化模型辨识过程中，针对有限频谱范围，提出了利用相干函数和功率谱密度加权综合，确定等效拟配的频率范围和频率节点的自适应方法，使得低阶等效拟配与输入激励信号高度相关，提高参数化模型辨识的精度、一致性和适应性。通过不同类型飞机的大量短时机动和少量扫频飞行试验数据模型辨识的工程应用示例，验证了动力学辨识优化方法算法稳定、结果准确，可满足飞行品质模态特性评价等应用需求。

辨识； 飞行试验； 短时机动； 有限频谱； Welch谱估计； 自适应； 低阶等效

对飞行器特定输入下的飞行试验数据进行飞行动力学系统辨识，获得应用于风洞试验数据校准、飞行控制系统设计和飞行品质评价等多个方面的支持数据，是飞行器研制工程中的一项重要工作。随着现代控制理论的发展和电传操纵系统的广泛应用，使得高增益飞机飞行动力学系统越来越复杂，也带来了动力学特性辨识的新问题。

时域辨识法是最早应用于飞行动力学模型系统辨识的方法，其主要优点是可以直接利用时域的飞行试验数据进行辨识，不存在中间过程误差。20世纪60年代，时域的输出误差法、最大似然法、卡尔曼滤波法在动力学系统辨识，特别是气动参数辨识中得到了广泛的应用，在早期的系统辨识研究中，一直占据着主导地位[1-2]。飞行器频域辨识法，其最早可追溯至1945年B-25J飞机传递函数辨识，随着快速傅里叶变换(FFT)算法的发展和计算能力的提升，从20世纪70年代，频域辨识法也有了很大的发展[3-6]。2006年，Klein和Morelli[4]系统地总结了频域辨识法中的极大似然法、输出误差法和方程误差法等。频域辨识法的主要优点是将线性微分方程或积分方程转化为代数方程而简化计算，而且可将被测数据选择在感兴趣的频率范围，具有较强的抗噪性能。虽然频域辨识法主要应用于线性系统辨识，但因其独特的优势，目前，依然是广泛应用的一种飞行器系统辨识方法。比如，美国系统技术公司(STI)和NASA历经较长周期开发了基于FFT技术的多种飞行动力学系统辨识软件[7-9]，特别是CIFER软件，采用Chirp-z变换和组合窗处理技术，提升频域辨识结果的精度，融入了多种数据处理方法，实现了多输入多输出的频域辨识，得到了广泛的工程应用[5]。

目前，由于大部分飞机依然是操纵姿态获得轨迹改变的“经典”飞行方式，因而其动力学描述仍可以用经典的模型结构，亦即仍然用“等效模型”的概念进行频域拟配获取系统模型，并进行飞行品质评价，也就是所谓的“三步法”频域辨识，包括数据预处理、时域-频域转换和频域等效拟配等步骤[10]。其中，从辨识算法的角度，时域-频域转换是其核心，常转变为功率谱密度的计算。经典谱估计以傅里叶变换为基础，具有计算结果稳定、效率高的优点，其主要缺陷是方差性能差，易受频率分辨率和窗口效应的影响。针对经典谱估计存在的问题，现代谱估计以模型为基础，利用采样数据建立模型，对数据进行外推，努力改善谱估计的分辨率，对短时数据具有更强的适应性，但也存在频率分辨率与信号的信噪比相关，谱估计质量受模型阶次影响和谱线分裂现象等不足[11]。

由于辨识算法问题本质是求“逆”问题，其求解过程和结果依赖于飞行试验数据的信噪比，受飞行试验输入激励类型、测量设备精度、系统干扰、飞行大气环境等因素的影响显著，特别是基于短时机动动作的试飞数据，增加了准确辨识频域特性的难度。针对此问题，最普遍的解决方法是，根据飞行试验目的，通过优化机动动作，来降低系统辨识的难度[12-14]。比如，美国空军和NASA特别建议，频域辨识法的适宜机动为数分钟的扫频输入信号[3,5,7]，德国DLR则推荐使用“3211”机动[5,10]，以得到较准确的辨识结果。但是，扫频、“3211”机动等优化机动虽然降低了系统辨识的难度，却与试飞工程的易实现性、安全性和经济性相矛盾，特别是扫频输入可能超出飞行员操纵预期，增大试飞风险。对于大型飞机来说，尤其是为获得横航向重要的荷兰滚模态，进行脚蹬扫频输入激励往往是难以实现的[15-17]。而降低试飞周期和耗费，也是试飞工程高度关注的重要问题。根据美国各种新机试飞统计，通常仅原型机本身试飞耗费，就占整个型号研制经费的10%～20%[17]。为此，在试飞工程中，期望采用脉冲、倍脉冲等较为简单的短时机动作为激励输入信号[16-17]。但是，短时激励信号频谱范围窄、信噪比低，即使CIFER等成熟的频域辨识软件对短时机动动作，往往也不能得到理想的动力学辨识结果[5,7]。

对于数秒时长的短时机动的系统辨识，2007年STI基于短时脉冲输入试飞数据(记录数据长度不足5 s)，研究了窄带宽特征(NBS)的系辨识法，采用小波变换理论和窄带巴特沃斯滤波技术辨识频域响应特性，获得了比传统FFT辨识法更理想的结果[7,18-20]。与加窗的傅里叶变换相比，小波变换具有更好的时间和频率分辨率，但也存在着理论复杂、小波基不唯一带来的小波基选取困难[21]。

在有人飞机飞行品质评价的工程应用中，根据驾驶员的频率感知和操纵特性，主要在0.1～10.0 rad/s频率范围内，根据有限频率点的频率响应特性，进行基于传递函数描述的响应模型的参数辨识并评价飞行品质[22-23]。

所以，综合上述试飞工程的安全性、经济性需求和有人驾驶飞机飞行品质评价的工程应用特点，飞行动力学辨识算法的关键问题，就是如何设计在较短的时间内尽量简单的机动，更好地获取所关心频率范围的响应特性问题。为此，本文针对短时机动飞行试验，以倍脉冲机动为重点，探讨基于谱估计进行时域-频域的高效、稳定转换，并进行基于最小二乘法的等效拟配频域系统辨识优化方法的研究。

1 短时倍脉冲机动的数据特征

如前所述，有人驾驶飞机飞行品质评价所关注的频率范围是基于驾驶员的感知灵敏度，一般在0.1～10.0 rad/s之间，具体与飞行模态的分布有关。表1给出了4种典型飞机的快变模态频率，可见，随着飞机尺寸量级的逐渐增加，其快变模态的频率呈逐渐下降趋势，对于有人驾驶飞机最大约为5.0 rad/s量级(轻小飞机)。因而，飞行品质规范设置的频率上限一般为10.0 rad/s[22-25]。而飞行品质评价的频率下限，主要考虑执行任务时飞行员的驾驶负担，一般设置为0.1 rad/s。

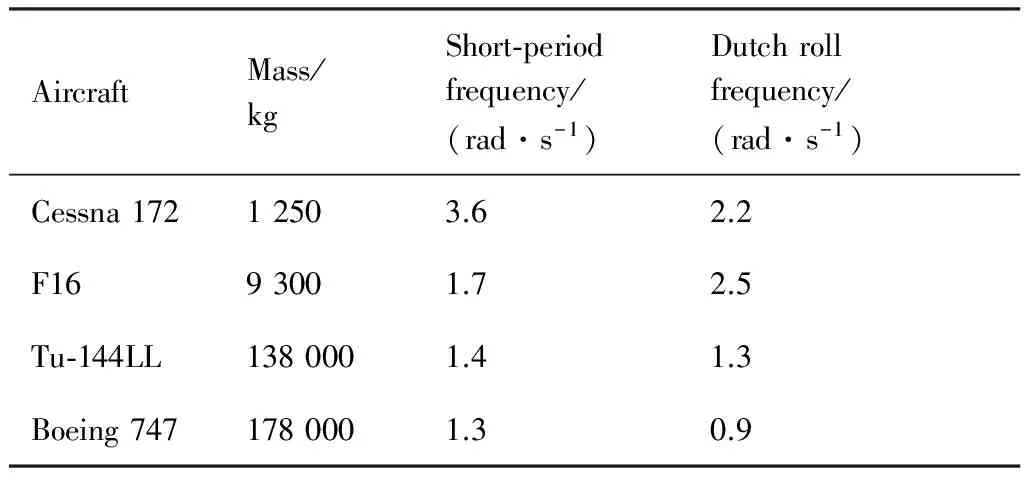
表1 典型飞机快变模态参数Table 1 Fast variable mode parameters of typical aircraft

从飞行品质评价的方法本身，尽管感兴趣的频带为0.1～10.0 rad/s，但是对于低频的模态(沉浮、螺旋等)，主要基于时域方法，通过考察其发散程度予以评估。应用等效拟配进行频域评估，重点针对高频模态(包括各类增稳形成的若干高频模态的综合)。飞行特性及其评价的物理本质为基于短时机动的频域辨识和品质评价方法建立了基础。

对于脉冲、倍脉冲、“211”等短时机动，倍脉冲的对称性最好，有利于消除不对称的稳态误差。当倍脉冲输入的主要频谱范围与预先估计的系统模态频率基本重合时，输入激励对系统模态频率范围有最强的激励作用。若预估的系统快变模态频率为ω，近似将倍脉冲看作是一个周期的正弦信号，则期望输入的倍脉冲时间周期为

T=2π/ω

(1)

通过适当调整倍脉冲宽度，调整所希望激发的频率范围。

倍脉冲激励信号的幅值，则要综合考虑响应不可超出结构模态边界或激发非线性特性，又不能太弱以致信噪比太低，或未激发出真实的模态响应特性，直接影响辨识精度。通常，对于迎角和侧滑角的响应峰峰值以3°～5° 为宜[14,18-19]。

典型的飞行试验输入输出时间历程如图 1所示，t为时间，δlon为纵向操纵输入，Nz为纵向过载，q为俯仰角速率。通常一个倍脉冲激励，其有效激励时间为1～5 s，由式(1)对应的频率范围约为1.2～6.3 rad/s，涵盖了主要有人驾驶飞机的快变模态范围(见表1)。在一个激励完成后，若飞机基本处于平衡状态，则可以继续进行下一个输入激励的飞行试验。

图1 飞行试验数据Fig.1 Flight test data

需要考虑的是，在倍脉冲激励的有效时间之外(如激励响应末端)，由于受到测量设备、大气扰动、系统死区和间隙等因素影响，短时机动测量的试验数据高频噪声可能很大，或者可能引入其他轴向的输入响应[17,19]。因而需要进行机动动作筛选，去掉明显的不协调数据。

2 短时机动时域-频域转换方法的改进

2.1 时域-频域转换基本理论

信号时域-频域转换可通过输入x(t)、输出y(t)时域响应数据的离散傅里叶变换，用离散的输出和输入幅值比和相位差数据点，来描述系统的输入-输出动态特性关系，在频域内建立非参数模型。

根据信号与系统理论，系统的频域特性为[11]

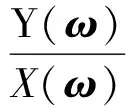
(2)

式中：Y(ω)、X(ω)分别为输出、输入的傅里叶变换，ω为频率；X*(ω)为X(ω)的共轭。式(2)将系统的频域响应特性计算，转变为输入输出的互功率谱密度函数Pxy(ω)和输入的自功率谱密度函数Pxx(ω)之比计算。

韦尔奇(Welch)平均周期图法功率谱估计[11]，把长度为N的数据XN(n)分成L段，如图2所示，每段的长度为M，段与段之间的重叠为M-K，第i个数据段经加窗后为

i=0,1,…,L-1;n=0,1,…,M-1

(3)

式中：w(n)为窗函数；K为整数；L为分段数。它们满足关系式

(L-1)K+M≤N

(4)

第i个数据段的周期图为

(5)

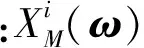
由此得到平均后的功率谱为

(6)

Welch平均周期图法功率谱估计，对于扫频等长时间尺度的机动动作，通过合理的选择窗函数类型、窗函数宽度及段间重叠，能获得更好的频率分辩率及方差性能。相反的，对于倍脉冲等短时机动来说，加窗引入了新的频域辨识误差，必须采用新的数据处理算法，消除Welch功率谱估计窗函数的边缘衰减效应。

评价输入和输出之间因果性的相干函数r2定义为

(7)

文献[5]指出，相干函数无跳变且r2≥0.6时，频域特性辨识结果是可接受的。

相干函数的引入对频域辨识很有意义。在非参数模型辨识阶段，根据相干函数可自动实现频域响应多窗口综合；在参数化模型辨识阶段，相干函数可以为模型等效拟配确定合适的频率范围，以强调高精度的频率响应数据点。

图2 Welch法加窗与重叠Fig.2 Windowing and overlap by Welch method

2.2 短时机动时域-频域转换的性能优化

为了提高谱估计的频域分辨率，获得功率谱的渐进无偏估计，谱估计理论与算法仍处于不断发展之中。Tischler和Remple提出了一种多窗频谱优化的方法，提高频谱的计算精度，从而使得(偏)相干函数和频率响应的计算更精确[5]。文献[5]指出，小的窗口宽度，增加了窗口平均个数，有利于辨识高频特性，但是对低频特性辨识精度下降。

针对短时机动时域-频域转换的性能优化需要，本文采用Tischler多窗口综合方法，扩展多窗口综合方式，提高频域辨识的精度；为了消减窗函数对短时机动的边缘衰减效应，探讨了平移机动动作的数据预处理方式。

1) 多窗口综合

多窗口综合通过定义多个不同宽度的窗口，进行多次辨识，利用相干函数对频域特性辨识结果进行自动加权综合，避免选择窗函数宽度对频域特性辨识结果的影响，提高频域特性辨识准确度。文献[5]的复合分窗方法，先对功率谱密度加权平均，再计算频率响应特性。本文探讨不同的窗口综合方法，即先计算多个窗口下频域响应特性，再进行加权平均平滑，达到减小频域辨识结果的方差的目的。

加权的依据是相干函数值，对依不同窗函数j辨识的高阶幅值|Gj(ω)|、相位∠Gj(ω)，加权综合公式为

(8)

(9)

对于加权后的频域特性，相应的用加权相干函数进行度量，定义为

(10)

图3 多窗口综合后频域响应对比Fig.3 Comparison of frequency-response with multi-windows composited

图3示出32、16、8和4 s不同窗口宽度得到的频域响应与多窗口综合的相应对比示例。可见，加权综合法保留了不同窗口宽度下有利的频响特征，得到了各频率下综合优化的辨识结果。

2) 窗函数边缘衰减效应的消减

为减少频谱能量泄漏，常采用哈明窗或海宁窗对飞行试验数据进行截断，获得较为真实的频谱[5,11]。数据长度为M的哈明窗表达式为

(11)

由于窗函数的非线性边缘衰减，在单个窗口的始端和末端均会丢失相关数据信息。Welch功率谱估计，通过窗口重叠抵消边缘缩减，避免引起频域响应辨识结果的偏差，这对长时扫频机动的飞行试验数据来说，通常易得到理想的结果。对于激励动作仅几秒的倍脉冲短时机动，有效信号可能仅出现在首个窗口左侧的非线性衰减边缘，这时窗口重叠不能抵消窗函数的边缘衰减效应，参见式(3)，示例如图4(a)所示。如果短时机动居于窗函数中心附近，窗函数的非线性影响可显著减弱，如图4(b)所示。

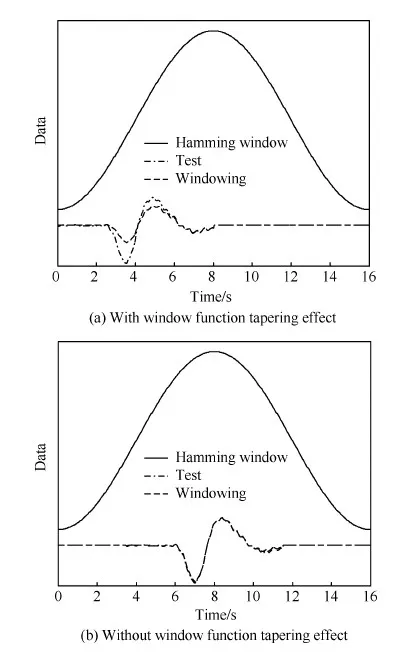
图4 窗函数对倍脉冲机动飞行试验数据的衰减Fig.4 Window function tapering to doublet maneuver flight test data

下面以短时机动频域响应辨识为例，进一步分析窗函数边缘衰减效应的影响。某飞机纵向升降舵δe到过载Nz的传递函数为

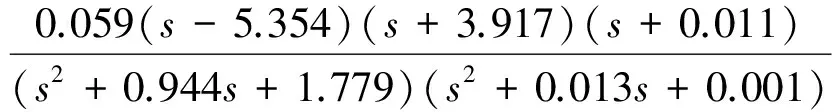
其短周期模态频率约1.34 rad/s，由式(1)，取倍脉冲机动时长4 s。为了对比分析，取哈明窗宽度为32 s。对比机动出现在首个窗口左侧非线性衰减区域(约6～10 s)和中心区域(约14～18 s)两组情况，频域辨识结果与传递函数计算的频域响应分别如图5(a)和图5(b)所示。

从辨识结果可知，对于倍脉冲激励，当激励靠近窗函数的中心，不存在严重的非线性边缘衰减效应时，频域辨识结果较准确(如图5(b)所示)，否则，将引起较大的结果偏差(如图5(a)所示)。对弱阻尼飞机状态，边缘衰减效应影响更大(有较大的谐振峰值误差)。所以，针对倍脉冲等短时机动，窗函数的边缘衰减效应必须避免。

图5 边缘衰减引起的频域辨识结果误差对比Fig.5 Comparison of frequency domain identification results error caused by windowing edge tapering effect

消减窗函数的边缘衰减效应核心是控制机动出现在窗函数中的位置。对于飞机品质评价频域辨识，为获得ωmin=2π/t≈0.1 rad/s的频率分辨率，可将时域数据长度圆整化为t≈64 s。考虑到快变模态不会低于0.2 rad/s，窗函数的最大窗口宽度不会超过32 s。因而辨识实施时，可以通过在短时机动前后补零、平移机动动作，或复制机动的方法，确保机动动作出现在窗函数中心。

3 基于短时机动的频率自适应等效拟配

在电传操纵飞机的飞行品质评价中，基于频域辨识法进行飞行特性的低阶等效拟配是重要环节。亦即根据试飞机动，通过确立适当的等效拟配模型结构，采用优化算法进行频域特性拟合，估计模型中的未知参数[3,5,22]，最终根据辨识的参数进行飞行品质的定量评价。

3.1 拟配频谱范围与拟配节点的自适应加权

对于现代特性迥异的电传操纵飞机，依据已有的飞行品质规范，如MIL-STD-1797A[23]进行等效拟配，经常存在拟配超出包线的情况。究其原因进行分析，有两种主要情况：① 试验激励机动没有充分激发0.1～10.0 rad/s的频率范围；② 被评飞机已经不能用某种经典的低阶等效模型进行描述。对于第①种情况，最理想的方法是进行扫频等试飞机动，但是这与高效、安全试飞相违背。而对于第②种情况，属于等效评价方法的本质问题，必须寻找新的品质评价方法[26-27]。如第1节所分析，等效拟配评价主要针对快变模态，所以等效该频段特性是关键。由此，本节寻找基于短时机动频谱特征，适应性的确定等效拟配的频率，获得精确的快变模态参数，实现飞机快变模态品质特性的准确、高效评价的目的。

在飞行试验过程中，短时机动主要激发感兴趣的飞机动态频率范围，且在这段有限的频率范围内，系统动态特性是可准确辨识的。等效拟配时，应增加该段频率范围的权重，而减弱或忽略其他未充分激发频段或辨识结果不可靠频段的权重。而频域特性自适应加权的依据是相干函数值(主要确定频率特性辨识有效频率范围)和功率谱密度(确定基于短时机动激发的拟配节点的位置)。

为此，建立等效拟配过程中自适应的选取拟配频率范围和频率点算法。

1) 设定等效拟配的频率点个数Nω和拟配频率范围[ωmin,ωmax]。

(12)

(13)

(14)

(15)

6) 取ωP序列权重为WωP(WωP∈[0,1])，一般可取等值权重WωP=0.5)，ωr序列的权重为1-WωP，得到综合加权的等效拟配频率节点序列为

(16)

3.2 等效拟配结果的验证

对某一飞机而言，在同一构型、飞行状态附近，工程上，往往进行多次输入激励，通过增加试验样本，获得系统辨识结果的渐近无偏估计，理论上，其等效拟配的参数化模型结果应是一致的。这种一致性，表明了系统辨识结果具有试验上的统计一致性，是系统辨识结果应达到的目标，也是评价辨识结果性能的一个标准[3,5,18,23]。

对于辨识模型失配的显著性水平评估，引入曲线拟合重合度指标[28]：

(17)

其中：2-范数为

(18)

3.3 示例和分析

以某大型运输类飞机(Ⅲ类)巡航飞行(B阶段)短时机动纵向飞行试验数据为例，考核前述优化算法。这里，优化算法进行了平移机动动作至窗函数中心的数据预处理、拟配频谱范围与拟配节点的自适应加权。

采用双拟配模型结构[23]，高阶和低阶等效的频域、时域响应和拟配节点、失配度对比结果如图6 所示，高度H=9 784 m，马赫数Ma=0.32，迎角α=3.2°。图6(a)、图6(b)分别为纵向操纵输入δlon到过载Nz和角速率q的常规方法高阶、低阶与优化方法高阶、低阶的频率响应对比。图6(c)、图6(d)分别为δlon到Nz和q的常规方法与优化方法的等效拟配节点和失配度对比。图6(e)为δlon输入下，Nz和q的试验数据、常规方法与优化方法的时域响应对比。

由图6(a)～图6(d)可见，在关心的短周期模态频率附近，优化算法高低阶频域响应重合性明显优于常规方法，可获得更准确的等效拟配模态频率、阻尼和系统等效延迟时间。图6(e)中的时域验证对比，也表明优化方法和飞行数据吻合，具有较强的真实飞行动力学特性等效能力。

优化算法的成功，不仅源于针对短时机动消减窗函数边缘衰减数据预处理方法，可获得更准确的频域响应特性，也与拟配频率范围与拟配节点的自适应加权算法，强调了谱密度能量和相干函数值较高的频率点相关。如图 7所示，分别给出了δlon和Nz、q的归一化功率谱密度曲线PSDδlon、PSDNz、PSDq，取均值后的功率谱密度(PSD composited)，和依自适应算法选择的等效拟配节点序列(Selected Matching Points)。由图6(c)、图6(d)和图7可知，对于短时机动，拟配节点主要集中在谱密度和相干函数值较高的频率。

概率密度的加权，使拟配频率与试验输入激励信号高度相关，当激励为扫频时，拟配频率自适应的扩展到接近0.1～10.0 rad/s的整个频率范围，并近似均匀分布。既能兼顾扫频宽频长时试验激励的整体性，又能适应倍脉冲等窄频短时试验激励的局部性。引入相干函数的加权，又考虑了表征输入、输出的线性相关性和频域特性辨识结果的可信度。这种拟配频率的自适应，在机动动作的频率特性与低阶等效拟配算法之间建立了紧密联系，增强了频域辨识法对不同输入激励信号的自适应性。

图6 参数化动力学模型频域辨识结果Fig.6 Parameterized dynamic model of frenquency domain identification results

采用优化算法，对算例飞机5个不同的倍脉冲激励低阶等效拟配参数，其均值(Mean)、标准差(Std)如表2所示。

由表2可知，等效拟配失配度较小，表明在关心的频率范围内，高低阶频域响应基本重合。不同机动的同一个拟配参数差异很小(如Std所示)，等效拟配结果具有较好的一致性。

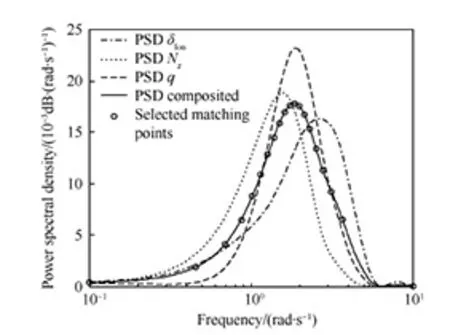
图7 功率谱密度曲线与拟配节点
Fig.7 Power spectral density curves and selected matching points

表2 纵向短周期等效拟配结果Table 2 Short-period parameters of LOES

ManeuverMismatch/dBDampingradioNaturalfrequency/(rad·s-1)Nume⁃ratorzero/sTimedelay/s149．90．4741．7120．7540．088228．90．4311．7240．7260．089319．90．5061．6360．6320．103417．10．6141．5780．5770．102563．10．4911．6230．5800．108Mean0．5031．6550．6540．098Std0．0550．0510．0670．007

图8 动力学辨识结果的时域一致性验证Fig.8 Time domain consistency verification of dynamic identification result

辨识结果的部分时域一致性验证，如图8所示，从高低阶时域响应对比来看，除了低阶等效模型不能复现飞行试验数据中存在高阶的扰动，在短周期模态频率附近，高低阶时域响应曲线重合很好。机动1～5与机动1高低阶对比的重合度指标，如表 3所示。表 3中，不同的机动动作的重合度指标，说明了参数模型真实的反映了被辨识的系统特性，和辨识结果的可靠性、一致性。通过其他不同类型飞机的大量短时机动和少量扫频飞行试验数据飞行动力学模型辨识的工程应用，也验证了拟配频率自适应的动力学频域辨识法，辨识结果准确、算法稳定可靠，可满足飞行品质模态特性评价等工程应用需求。

表3动力学模型辨识对不同机动的一致性

Table3Comparisonofidentificationresult’sconsistencyofdynamicmodelfordifferentmaneuvers

ManeuverFlightstateH/kmMaα/(°)F(Nz)/%F(q)/%19．70．333．287．288．82vs19．80．323．287．789．43vs19．80．323．180．089．04vs19．70．323．678．588．15vs19．70．323．581．190．7

4 结 论

针对有人驾驶飞机飞行试验高效、安全获取飞行动力学特性和飞行品质评价的问题，进行试飞参数辨识方法改进研究，得到：

1) 针对短时倍脉冲机动输入作为激励的有利试飞实施方式，以加权相干函数作为主要衡量指标，提出了窗函数边缘衰减效应消减的数据预处理方法，并推广Tischler多窗口综合方法，取得了频域特性辨识结果精度的明显改进。

2) 从避免试飞机动的分散性可能导致飞行品质辨识结果的分散性问题着手，为了提高评价结果的一致性及重合度，提出了相干函数与功率谱密度综合加权的频率自适应辨识方法，使得低阶等效拟配与输入激励信号高度相关，能同时兼顾宽频长时机动和窄频短时机动频域辨识法参数化模型辨识的自适应性。

上述算法改进，构成了基于短时机动的飞行品质评价的重要基础，试验证明能够适应电传操纵等具有更多、更丰富模态飞机的评价需求。

[1] JATEGAONKAR R V. Flight vehicle system identification: A time domain methodology[M]. Reston: AIAA, 2006: 9-14.

[2] HAMEL P G, JATEGAONKAR R V. Evolution of flight vehicle system identification[J]. Journal of Aircraft, 1996, 33(1): 9-28.

[3] MORELLI E A. Identification of low order equivalent system models from flight test data: NASA/TM-2000-210117[R].Washington, D.C.: NASA, 2000.

[4] KLEIN V, MORELLI E A. Aircraft system identification: Theory and practice[M]. Reston: AIAA, 2006: 1-4.

[5] TISCHLER M B, REMPLE R K. Aircraft and rotorcraft system identification: Engineering methods with flight test examples[M]. Reston: AIAA, 2006:1-35, 135-190.

[6] 蔡金狮, 汪清, 王文正, 等. 飞行器系统辨识学[M]. 北京: 国防出版社, 2003: 221-245.

CAI J S, WANG Q, WANG W Z, et al. Aircraft system identification[M]. Beijing: National Defense Industry Press, 2003:221-245 (in Chinese).

[7] KLYDE D H, BACHELDER E N, THOMPSON P M, et al. Flying qualities parameter identification using short duration flight test inputs[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Reston: AIAA, 2007： 1-13.

[8] WANG K C, ILIFF K W. Retrospective and recent examples of aircraft parameter identification at NASA Dryden Flight Research Center[J]. Journal of Aircraft, 2004, 41(4): 752-764.

[9] MORELLI E A, KLEIN V. Application of system identification to aircraft at NASA Langley Research Center[J]. Journal of Aircraft, 2005, 42(1): 12-25.

[10] JATEGAONKAR R V, FISCHENBERG D, GRUENHAGEN W. Aerodynamic modeling and system identification from flight data-recent applications at DLR[J]. Journal of Aircraft, 2004, 41(4): 681-691.

[11] 胡广书. 数字信号处理理论、 算法与实现[M]. 北京: 清华大学出版社, 2012: 507-590.

HU G S. Theory, algorithm and implementation of digital signal processing[M]. Beijing: Tsinghua University Press, 2012: 507-590 (in Chinese).

[12] HAMEL P G, JATEGAONKAR R V. The role of system identification for flight vehicle applications-revisited[C]//Proceedings of RTO-SCI Symposium on “System Identification for Integrated Aircraft Development and Flight Testing”, RTO-MP. Neuilly-Sur-Seine： RTO/NATO， 1999: 2.1-2.12.

[13] NETO N S B, HEMERLY E M. Parameter estimation flight test maneuver optimization considering measurement colored residuals[C]//25th International Congress of the Aeronautical Sciences. Hamburg： ICAS， 2006： 1-10.

[14] MORELLI E A. Flight test validation of optimal input design and comparison to conventional inputs[C]//AIAA Atmospheric Flight Mechanics Conference. Reston: AIAA, 1997: 11-13.

[15] THEODORE C R, IVLER C M, TISCHLER M B, et al. System identification of large flexible transport aircraft[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Reston: AIAA, 2008: 6894.

[16] 李雅静, 刘旭华. 频域响应辨识优化方法研究[J]. 飞行力学, 2014, 32(4): 342-346.

LI Y J， LIU X H. Optimization technique of frequency domain response identification[J]. Flight Dynamics, 2014, 32(4): 342-346 (in Chinese).

[17] 周自全. 飞行试验工程[M]. 北京: 航空工业出版社， 2010: 4-10.

ZHOU Z Q. Flight test engineering[M]. Beijing: Aviation Industry Press, 2010: 4-10 (in Chinese).

[18] BACHELDER E, THOMPSON P, KLYDE D, et al. A new system identification method using short duration flight test inputs[C]//AIAA Atmospheric Flight Mechanics Conference. Reston: AIAA, 2011: 4059-4081.

[19] KLYDE D H, BACHELDER E N, MCMAHON R, et al. Use of in-flight simulation to create a flying qualities database: AIAA-2008-1624[R]. Reston: AIAA, 2008.

[20] BACHELDER E N, KLYDE D H, LEE D, et al. Dynamic detection of actuator frequency response[C]//43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Joint Propulsion Conferences. Reston: AIAA, 2007: 1-13.

[21] BOGGESS A, NARCOWICH F J. A first course in wavelets with Fourier analysis[M]. Hoboken： John Wiley & Sons, 2015: 234-268.

[22] HODGKINSON J. A history of low order equivalent systems for aircraft handling qualities analysis and design[C]//2003 AIAA Atmospheric Flight Mechanics Conference and Exhibit. Reston: AIAA, 2003: 11-14.

[23] STANDARD M. Flying qualities of piloted aircraft: MIL-STD-1797A[R]. Langley： Department of Defense, 2004: 183-280.

[24] DOROBANTU A, MURCH A, METTLER B, et al. System identification for small, low-cost, fixed-wing unmanned aircraft[J]. Journal of Aircraft, 2013, 50(4): 1117-1130.

[25] CARNDUFF S D. System identification of unmanned aerial vehicles[D]. Canfield： Canfield University, 2008.

[26] 谭文倩, 张曙光. 飞机横航向等效拟配模型的对比研究[J].飞行力学, 2003, 21(4): 14-18.

TAN W Q, ZHANG S G. Research on the models of lateral and directional equivalent matching for an aircraft[J]. Flight Dynamics, 2003, 21(4): 14-18 (in Chinese).

[27] 张曙光, 方振平, 高立华. 纵向大迎角飞行品质对参数的灵敏度分析[J]. 飞行力学， 1999， 17(2): 1-6.

ZHANG S G, FANG Z P, GAO L H. Analysis on sensitivity of high angles of attack longitudinal flying qualities to variation of parameters[J]. Flight Dynamics, 1999, 17(2): 1-6 (in Chinese).

[28] LENNART L. MATLAB R2012b system identification toolbox reference[M/OL]. Natick： MathWorks， 2012： 131-139 (2012-09)[2016-08-15]. www.mathworks.com.

(责任编辑： 鲍亚平)

An optimization method for dynamic identification based onshort-duration maneuvering flight test data

WANGBaoyin1,ZHANGShuguang1,*,JIAXiaopeng2

1.SchoolofTransportationsScienceandEngineering,BeihangUniversity,Beijing100083,China2.InstituteofAircraft,ChineseFlightTestEstablishment,Xi’an710089,China

How to generate the accurate response at the frequency range of interest from the maneuvering is one of the significant problems for dynamic identification. Although short-duration doublet is commonly used in flight test activities and is easy to implement with a good consideration of both security and economy, it is difficult to get the accurate estimation due to its limited spectrum and lower signal to noise ratio. Thus, a method focusing on improving estimation accuracy based on the short-duration maneuvering flight test data is developed in this paper. The main factors that affect the accuracy of the non-parametric model identification in the classical Welch method of spectrum estimate are analyzed. A novel data pre-processing method which can taper the window function edge is presented, and the multi-window composite technology is integrated to improve the identification accuracy. Regarding the limited frequency spectrum, an adaptive low-order equivalent matching method is developed to select the frequency range and node based on a weighted function of coherence function and power spectral density. This method make the low-order equivalent matching highly correlated with the maneuvering input signal, and improve the accuracy, consistency and adaptability of the model parameter identification. The dynamic identification optimization technique is applied to a large amount of short-duration maneuvering and several sweeping flight test data for various types of aircrafts. The results meet the accuracy requirement for flight quality evaluation application, while the algorithm is stable and reliable.

identification; flight test; short-duration maneuver; limited frequency spectrum; Welch method of spectrum estimate; adaptive; lower-order equivalent

2016-09-26；Revised2016-10-25；Accepted2016-11-09；Publishedonline2016-11-211439

2016-09-26；退修日期2016-10-25；录用日期2016-11-09； < class="emphasis_bold">网络出版时间

时间：2016-11-211439

www.cnki.net/kcms/detail/11.1929.V.20161121.1439.014.html

*

.E-mailgnahz@buaa.edu.cn

王保印， 张曙光， 贾晓鹏． 一种基于短时机动试飞数据的动力学辨识优化方法J． 航空学报,2017,38(6):120815.WANGBY,ZHANGSG,JIAXP.Anoptimizationmethodfordynamicidentificationbasedonshort-durationmaneuveringflighttestdataJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):120815.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0293

V212.1

A

1000-6893(2017)06-120815-12

URL：www.cnki.net/kcms/detail/11.1929.V.20161121.1439.014.html

*Correspondingauthor.E-mailgnahz@buaa.edu.cn