适用于参数可调结构的非定常气动力降阶建模方法

王梓伊， 张伟伟

西北工业大学 航空学院， 西安 710072

适用于参数可调结构的非定常气动力降阶建模方法

王梓伊， 张伟伟*

西北工业大学 航空学院， 西安 710072

基于计算流体力学(CFD)的非定常气动力降阶模型(ROM)可以极大提高气动弹性分析效率，然而现有的ROM只能针对固定参数结构，即只适合于固定模态振型，这使得现有ROM在气动弹性优化设计和不确定性分析等结构变参问题中应用受限。针对该问题，在文献[20]基础上提出了一种新的适用于任意模态振型的非定常气动力建模方法。首先将待设计/分析的结构进行参数化抽样和模态分析，之后通过主成分分析(PCA)得到若干基振型，再将这些基振型线性叠加即可拟合抽样空间内任何参数下结构的前若干阶振型。当结构参数改动时，仅仅是叠加系数发生变化。算例表明，仅用很少的基振型就能达到理想的拟合精度。经典的气动力降阶方法可用于基振型坐标下的气动力降阶，进一步变换可得到适用于不同结构的ROM，这意味着，结构参数可以在抽样空间内任意调节改动，而ROM却是通用的。该方法能广泛用于气动弹性优化设计和不确定性分析工作，可提高颤振分析精度和效率。

结构优化； 参数变动； 降阶模型(ROM)； 跨声速流； 颤振； 非定常气动力

为了提高气动弹性分析的效率，工程上常借助线化势流理论来计算气动力，然而，该方法并不适用于跨声速和大迎角的情况。由于大型客机和大型运输机等飞行器的巡航速度处于跨声速区，并且很多歼击机也需要在跨声速区保持必要的作战性能，在这种情况下，基于线化理论的非定常气动力建模方法便不再适用。随着CFD技术的发展，直接基于CFD的求解方法为跨声速区气动弹性问题提供了新的解决思路，但由于该方法需要消耗大量的计算资源和时间成本，因此目前主要用作后期验证。

为了降低CFD方法分析气动弹性问题的计算成本，很多学者进行了气动力降阶方法相关研究。Dowell[1]、Lucia[2]、张伟伟[3]和陈刚[4]等对非定常气动力降阶建模方法及其在气动弹性分析中的应用做了详细论述。可以看到，在非定常气动力降阶中，主要应用了两种方法：本征正交分解(Proper Orthogonal Decomposition, POD)法和系统辨识方法。系统辨识方法包括积分方法和差分方法，比如Volterra级数方法属于积分方法，而ARX(Auto Regressive with eXogenous input)模型则属于差分方法。在文献[5-7]中，基于ARX模型的非定常气动力降阶建模方法已经应用于带操纵面机翼的跨声速颤振分析[5]、大迎角颤振分析[6]、跨声速颤振主动抑制控制率设计[7]等实际问题。在文献[8-10]中，非定常气动力降阶建模方法已经应用于跨声速极限环振荡分析。在这些分析中，非定常气动力降阶模型(ROM)(如POD[8]、Volterra级数[9]、ARX模型[10])是静态非线性、动态线性的，极限环振荡的非线性来源于结构的非线性。对于跨声速流动中小振幅的颤振分析，这些非定常气动力降阶模型是适用的。在文献[11-15]中，径向基函数神经网络模型已经用于构建跨声速流动中动态非线性的非定常气动力降阶模型。这些非定常气动力降阶模型成功预测了结构线性、气动力动态非线性的极限环振荡。

尽管取得很大进展，但上述ROM方法只能针对给定结构。当结构发生改动时，模态频率和模态振型一般都会随之变化。目前，模态坐标下的气动力模型能够适应模态质量或模态频率的变化[16-17]，却不能适应模态振型的变化。文献[18-19]表明，如果仅考虑模态频率而忽视模态振型的变化，颤振预测的结果将不可信。换言之，一旦结构改动并引发振型变化，就必须重新建立适用于新振型的ROM，这就需要再次启动CFD求解器以采集训练数据。在气动弹性优化设计中，如果将颤振速度作为优化问题的一个约束条件来优化结构参数(如梁的位置、蒙皮厚度等)，那么，优化过程中需要不断地计算不同结构参数下的颤振速度，也就必须不断地调用CFD求解器，计算量极大；此外，在考虑到气动弹性问题的不确定性设计中，同样会面临计算量巨大的挑战。

为解决这个问题，文献[20]提出了一种适用于任意振型的非定常气动力降阶方法(ROM suitable for Arbitrary Mode Shapes, ROM-AMS)。首先寻找一组数学意义上的基模态振型，这些基模态振型以正确的系数线性叠加，可以复现出真实振型。文献[20]中的基模态振型为一组分布在机翼平面上具有不同中心位置的径向基函数。之后在基模态坐标下，构建基振型的非定常气动力模型，在基模态空间和模态空间之间变换后，该模型就可以取代非定常CFD求解器，进而用于颤振分析。同时，该模型继承了之前ROM在较宽频率内对不同模态频率的适应能力。在保证精度的前提下，该方法计算量仅为秒级。

然而，上述方法使用基振型数量较多，在模型训练和辨识中会消耗较多时间，并且对于高阶振型或复杂外形的拟合精度不足，可能导致颤振速度误差放大。对此，本文利用主成分分析(PCA)方法来构建基振型。首先选取若干具有代表性的结构样本，通过PCA分析得到基振型，同文献[20]一样，这里的基振型仅具有数学意义。分析表明，只需要很少的基振型就能达到较高精度的拟合，减少了计算量。之后，沿用文献[20]的思路，构建适用于不同结构参数的非定常气动力降阶模型。

1 非定常气动力降阶模型

1.1 适用于给定振型的非定常气动力降阶模型

首先选择可能发生颤振耦合的前n阶法向振型Φ1(p)，Φ2(p)，…，Φn(p)，p为有限元节点坐标。为每阶振型设计激励信号ξ1，ξ2，…，ξn，之后调用CFD求解器，并使物面边界网格按给定的运动形式做强迫运动，运动形式为

(1)

求解该运动形式下流场的前阶气动力响应(振型的广义气动力系数)F1，F2，…，Fn：

(2)

式中：p为当地压强；q为来流动压；ds为面积微元。于是得到了用于训练气动力模型的激励响应数据对。之后选择离散型多输入多输出差分模型建立基于振型的非定常气动力降阶模型：

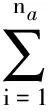
(3)

式中：k′为时间步；F为系统输出向量(n阶广义气动力系数)；ξ为系统输入向量(n阶广义位移)；Ai和Bi为待辨识矩阵；na和nb为由用户决定的模型延迟阶数。利用获得的训练数据，通过最小二乘方法求出式(3)中的待辨识矩阵，建立基于振型的非定常气动力降阶模型。

由于必须事先给定振型，因此，式(3)中的模型被称为适用于给定结构(即给定振型)的非定常气动力降阶模型，即ROM-PMS，将该模型应用于颤振分析(见1.4节)，可以快速预测机翼的颤振特性。但当模态振型随内部结构改动而发生改变时，就需重新调用CFD求解器采集训练数据，并建立基于新模态振型的气动力模型，这使得在气动弹性优化设计和气动弹性不确定性设计等应用中，ROM-PMS方法的计算量依然巨大。因此，需设法建立适用于任意振型的非定常气动力降阶模型，即ROM-AMS。

1.2 构建基振型

文献[20]用径向基函数法生成基振型，见图1。如图2所示，在机翼平面上选择若干节点，每个节点上设置一个径向基函数。按照正确的系数线性叠加后，这些径向基函数就能拟合出完整的模态振型。当结构改变引起振型改变时，只需要修正叠加系数，就能拟合出新的振型，而径向基函数本身不变。于是，在某个节点处按照图1形状隆起的机翼平面就可以作为基振型。不同基振型在不同的节点处隆起，显然，节点越密集，所需基振型越多，拟合精度越高。

为保证拟合精度，该方法需要较多的基振型，即便如此，高阶模态或复杂气动外形拟合精度依然不足。因此，本文使用PCA方法生成基振型。

图1 机翼表面径向基函数Fig.1 Radial basis function of wing surface

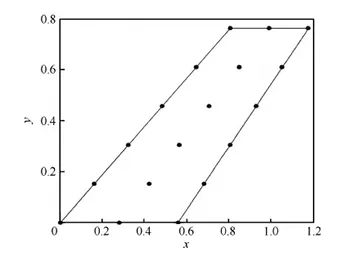
图2 机翼表面节点分布Fig.2 Locations of basis points of wing surface

首先，在设计变量构成的空间内进行抽样，得到n个结构样本，进行模态分析后，每个样本取前k阶模态振型，于是得到了kn个振型Φi(p)，i=1,2,…,kn，并将其作为PCA分析的输入向量。分析完成后，取对应特征值较大的前m个特征向量作为基振型φi(p)，i=1,2,…,m，m的大小取决于拟合精度要求。相比于径向基函数法，PCA方法所需基振型数量很少，拟合精度高，但需要在优化开始前在变量空间内进行抽样，并且抽样质量会影响拟合效果。

1.3 适用于任意振型的非定常气动力降阶模型

记某结构的j阶模态振型为Φj(p)，其中j=1,2,…,k,k为需要分析的模态总阶数。Φj(p)可用基振型φi(p)表示为

(4)

式中：γij为用来拟合j阶模态振型的第i个基振型的叠加系数。该系数实际上就是振型向量在基振型坐标下各轴上的投影。

之后用经典的气动力降阶方法建立基振型的ROM。首先为每个基振型设计激励信号，这里的信号需要有足够宽的频带。基振型乘以相应的激励信号，相加得到激励过程中动网格的变动位移。这里同样使用ARX模型建立非定常气动力降阶模型

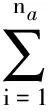
(5)

式中：t为时间步；f为输出量，即基模态广义气动力系数；u为输入量，即基模态广义位移。调用CFD求解器得到各阶基模态的响应后，即可通过最小二乘法得到式(5)中的待辨识矩阵。

需要注意，当前的气动力模型只能由基模态的广义位移计算出关于基模态的广义气动力系数，若要用于任意结构的颤振分析，气动力模型还必须包含两步转化：

1) 将广义位移转化为基广义位移(对应图3中的Transformation 1)。

已知某机翼的k阶模态振型Φ1(p),Φ2(p),…,Φk(p)，以及对应的k个广义位移ξ1,ξ2,…,ξk，式(1)重写为

(6)

将式(4)代入式(6)，得

(7)

式中：

(8)

其中：u1,u2,…,um被定义为基广义位移，输入到基振型ROM中。

2) 将基广义气动力系数转化为广义气动力系数(对应图3中的Transformation 2)。

基模态的广义气动力系数定义为

(9)

得到关于基振型的响应f1,f2,…,fm后，按式(10)转化为真实模态的广义气动力响应F1,F2,…,Fk：

(10)

上述两步转化的实质是输入与输出在模态坐标系和基模态坐标系之间的变换，这使得气动力模型具备了由广义位移计算出真实振型的广义气动力系数的能力。而当结构发生变动时，仅仅是式(8)和式(10)中的系数发生变化，因此，ROM-AMS能极大提升气动弹性优化设计和不确定性分析的效率。具体流程图见图3。

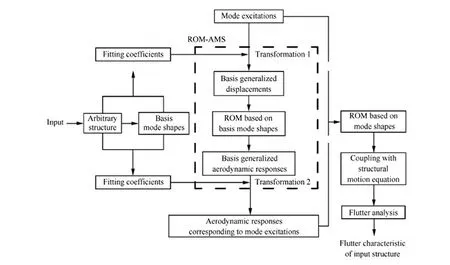
图3 ROM-AMS的颤振分析流程Fig.3 Flowchart of flutter analysis through ROM-AMS

1.4 颤振分析方法

将气动力模型转化为连续形式的状态空间方程，得

(11)

在模态坐标系下，结构运动方程为

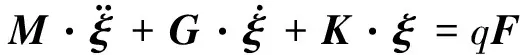
(12)

式中：M、G、K由该结构的有限元分析结果确定。将式(12)转化为连续型状态空间方程

(13)

式中：xa和xs为状态空间变量；Aa、As、Ba、Bs、Ca、Cs、Da和Ds均为状态空间方程矩阵。

耦合式(11)和式(13)，得到气动弹性系统的状态空间方程

(14)

这样，气动弹性系统的稳定性分析可转化为求解系统稳定性判断矩阵A的特征值问题。通过求解不同动压下A的特征值，制成v-g图和v-ω图，进而研究机翼的颤振特性。具体的推导过程见文献[6]。

2 算 例

图4 切尖三角翼试验模型和配重挂载位置Fig.4 Clipped delta wing test model and positions of concentrated mass

表1 原试验模型的模态频率Table 1 Modal frequency of original test model

选择切尖三角翼试验模型作为研究算例[21]，通过挂载配重并改变其位置来模拟结构的变化。如图4所示，机翼的二元板结构被圆形实线分割成两个部分：圆形的配重和机翼其余部分。图中c为弦长，b为展长。配重的圆心位置由弦向和展向的虚线交叉确定，通过改变虚线位置参数b1和c1进而改变配重的位置。配重质量约为0.1 kg，机翼其余部分质量约为0.24 kg。表1对比了原试验模型模态频率f的Nastran数值解和试验解[21]，说明Nastran进行结构分析精度足够。图5对比了样本6和样本61的前两阶模态振型，可以看到，配重位置的改变会对振型产生较大影响，而后两阶振型变化更大，限于篇幅并未展示。这样的改变程度足以模拟工程中的复杂结构变动带来的振型变化。

首先需要找出一组基振型，使得无论将配重挂载于图4阴影区域的哪个位置，对应结构的前4阶模态振型都能由基振型线性叠加拟合得到。如图4所示，改变b1和c1生成64个挂载点各异的样本。例如，6号结构的挂载点位于阴影区域左侧边线(标有“6”的位置)，61号结构的挂载位置为该区域右侧边线。获得这些样本结构的前4阶振型后，进行PCA分析，选取对应特征值较大的前6个特征向量作为基振型，如图6所示。

为了表征基振型拟合实际振型的精度，这里引入MAC(Modal Assurance Criteria)值[20]。

图5 典型结构的前2阶模态振型云图Fig.5 The first 2 mode contour of vibration shapes of typical structures

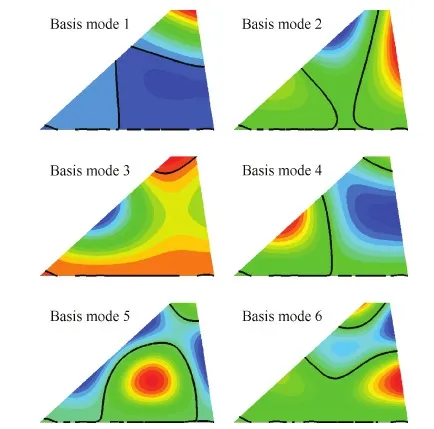
图6 前6阶基模态振型Fig.6 Mode vibration shapes of first 6 basis modes

表2 样本6和样本61的MAC值Table 2 MAC value of the 6th and the 61st samples

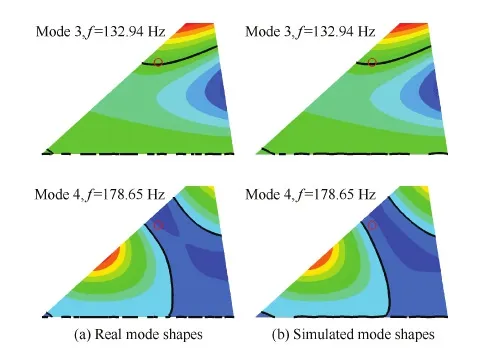
图7 样本6的3、4阶模态振型Fig.7 The 3rd and 4th mode of vibration shapes of the 6th sample

式(15)中，Φ*为基模态拟合出的振型，Φ为对应的真实振型。MAC值越接近1，表示拟合精度越高。基振型的拟合效果见表2和图7。由于3、4阶振型拟合难度更大，故图7仅显示3、4阶振型以说明问题。

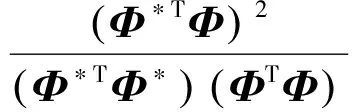
(15)

图8为基振型数量对拟合精度的影响。以样本6为例，可以看到，当基振型选取数量少于4时，各阶振型拟合精度依然不足，尤其是高阶振型，由于其形状复杂，拟合精度更差。但随着选取基模态阶数的增加，4阶模态都达到了较高精度，仅选取4个基模态时，4阶振型的MAC值就已经接近1，这种效果是径向基函数(RBF)方法难以达到的。算例选取了前6阶基振型，因此拟合精度足够。

图8 基振型选取数量对MAC值的影响(样本6)Fig.8 Influence of selected basis mode number on MAC value (the 6th sample)

图9 真实模态和基模态振型的激励信号Fig.9 Excitations signal of real mode shapes and basis mode shapes

之后验证ROM-PMS的准确性。使用图9(a)中的信号激励原试验模型的前4阶模态，用CFD求解Ma=0.87，来流密度为0.41 kg/m3时各阶对应的广义气动力。颤振动压实验值为16 548 Pa[22]，而ROM-PMS结果为17 155 Pa，相对误差仅为3.66%。

采用与ROM-PMS相同的流场条件，建立基振型的ROM。使用图9(b)的信号激励6阶基模态，得到广义气动力响应后，训练ARX模型，输出输入延迟阶数均为12。图10表明，ROM-AMS获得的广义气动力系数响应具有较高的精度。

算例使用了7个参考样本来验证求解精度，如图11所示。使用ROM-AMS方法得知，样本6 和样本61分别为颤振临界速度最大和最小的样本。图12和表3对比了ROM-AMS和ROM-PMS进行颤振分析的结果，说明ROM-AMS方法具有较高的精度。最后，通过ROM-AMS方法得出的挂载点位置对颤振速度的影响如图13所示。

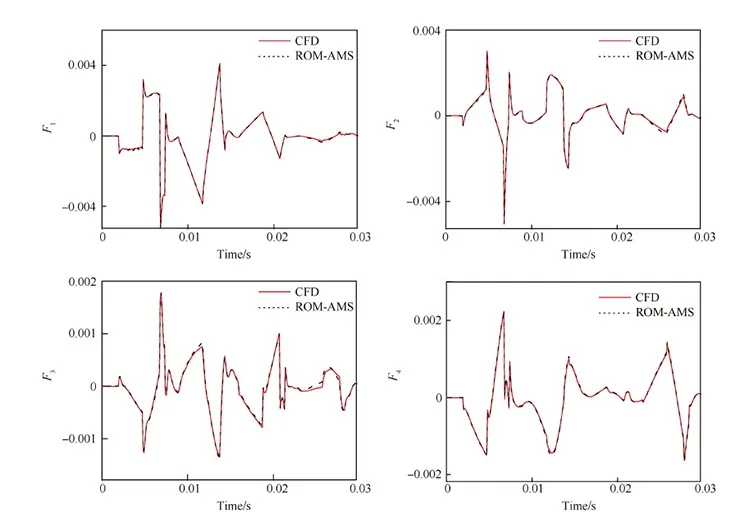
图10 样本6对应于图9(a)中激励的气动力响应Fig.10 Aerodynamic responses corresponding to mode excitations presented in Fig.9(a) for the 6th sample

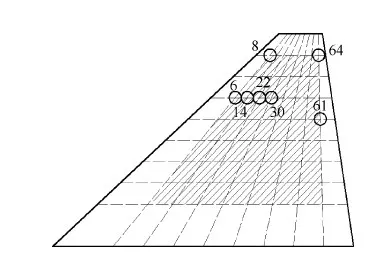
图11 参考样本的挂载点位置Fig.11 Positions of concentrated mass of reference samples

以上算例均在具有8核CPU、3.6 GHz主频和8 G内存的工作机上运行，计算时间对比如表4 所示。可以看到，在计算单个结构的颤振特性时，ROM-AMS方法要比ROM-PMS方法多约60%的计算量，但如果需要计算1 000个结构，ROM-PMS方法需要消耗大约2 500 h，即104.1 d，而ROM-AMS仅需约15.5 h，因此，ROM-AMS方法适用于需要分析大量结构的气动弹性优化设计和不确定性设计。

图12 样本6的颤振分析结果Fig.12 Flutter analysis results for the 6th sample

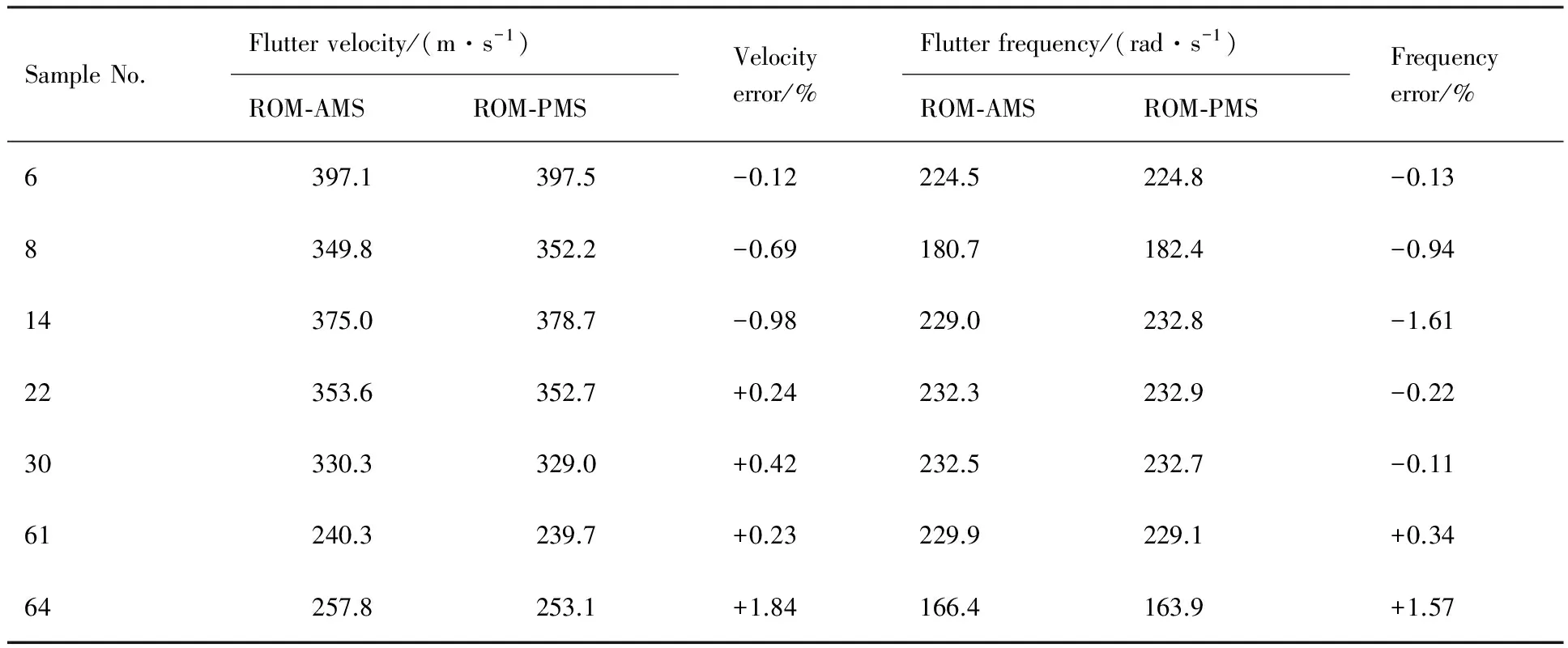
表3 ROM-AMS与ROM-PMS方法结果对比Table 3 Comparison of solutions of ROM-AMS and ROM-PMS methods

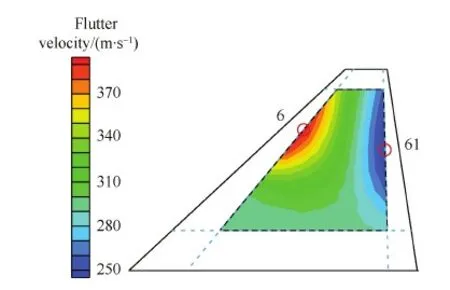
图13 挂载点位置对颤振速度的影响Fig.13 Influence of concentrated mass position on flutter velocity

表4ROM-AMS和ROM-PMS方法颤振分析的计算时间

Table4ComputationalcostofROM-AMSandROM-PMSmethodsflutteranalysis

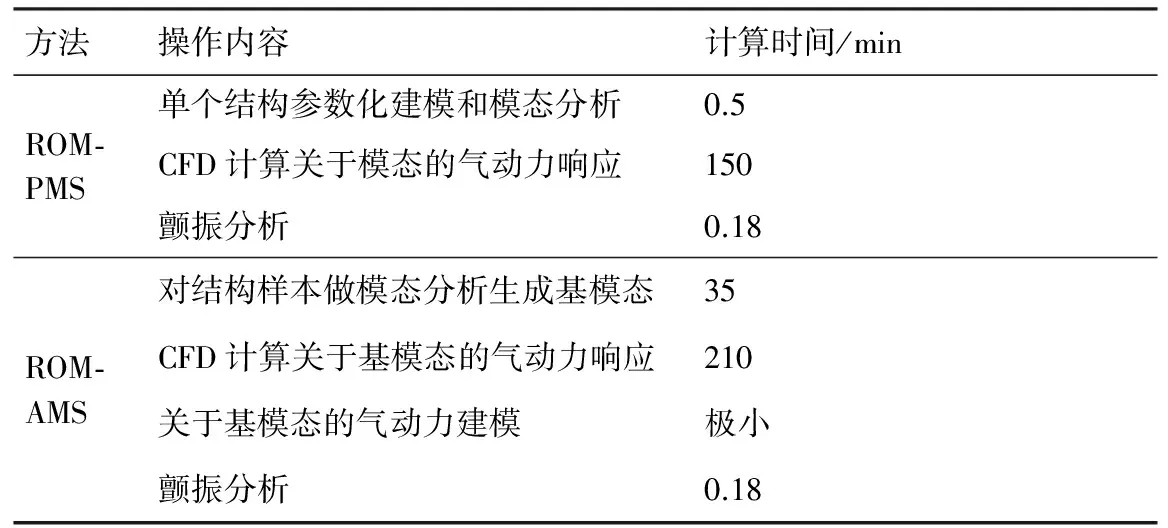
方法操作内容计算时间/minROM⁃PMS单个结构参数化建模和模态分析0．5CFD计算关于模态的气动力响应150颤振分析0．18ROM⁃AMS对结构样本做模态分析生成基模态35CFD计算关于基模态的气动力响应210关于基模态的气动力建模极小颤振分析0．18

3 结 论

1) 相比于径向基函数法，PCA方法拟合抽样空间内任意结构振型尤其是高阶振型精度更高，同时使用基振型数量较少。

2) ROM-AMS不仅继承了之前降阶方法对模态频率在较宽频域内变化的适应能力，同时也能适应振型的较大变化，因此具有相同气动外形下变结构的适应能力。

3) 适用于任意模态振型的气动力建模方法，能够快速准确地得到优化范围内任意结构的颤振特性，且求解的颤振速度和频率精度较高。

综上，本文提出的气动力建模方法能够适用于变动参数的不同结构，为之后的气动弹性优化设计和气动弹性不确定性设计打下了基础。

[1] DOWELL E H, HALL K C. Modeling of fluid-structure interaction[J]. Annual Review of Fluid Mechanics, 2001, 33(1): 445-490.

[2] LUCIA D J, BERAN P S, SILVA W A. Reduced-order modeling: New approaches for computational physics[J]. Progress in Aerospace Sciences, 2004, 40(1-2): 51-117.

[3] 张伟伟, 叶正寅. 基于CFD的气动力建模及其在气动弹性中的应用[J]. 力学进展, 2008, 38(1): 77-86.

ZHANG W W, YE Z Y. On unsteady aerodynamic modeling based on CFD technique and its applications on aeroelastic analysis[J]. Advances in Mechanics, 2008, 38(1): 77-86 (in Chinese).

[4] 陈刚， 李跃明. 非定常流场降阶模型及其应用研究进展与展望[J]. 力学进展, 2011, 41(6): 686-701.

CHEN G, LI Y M. Advances and prospects of the reduced order model for unsteady flow and its application[J]. Advances in Mechanics, 2011, 41(6): 686-701 (in Chinese).

[5] 张伟伟, 叶正寅. 操纵面对跨声速机翼气动弹性特性的影响[J]. 航空学报, 2010, 66(7): 999-1007.

ZHANG W W, YE Z Y. Effect of control surface on airfoil flutter in transonic flow[J]. Acta Aeronautica et Astronautica Sinica, 2010, 66(7): 999-1007 (in Chinese).

[6] ZHANG W W, YE Z Y. Reduced-order-model-based flutter analysis at high angle of attack[J]. Journal of Aircraft, 2007, 44(6): 2086-2089.

[7] ZHANG W W, YE Z Y. Control law design for transonic aeroservoelastic[J]. Aerospace Science and Technology, 2007, 11(2-3): 136-145.

[8] DOWELL E H, THOMAS J P, HALL K C. Transonic limit cycle oscillation analysis using reduced order aerodynamic models[J]. Journal of Fluids and Structures, 2004, 19(1): 17-27.

[9] BERAN P S, LUCIA D J, PETTIT C L. Reduced-order modeling of limit-cycle oscillation for aeroelastic systems[J]. Journal of Fluids and Structures, 2004, 19(5): 575-590.

[10] JONES D P, ROBERTS I, GAITONDE A L. Identification of limit cycles for piecewise nonlinear aeroelastic systems[J]. Journal of Fluids and Structures, 2007, 23(7): 1012-1028.

[11] ZHANG W W, WANG B B, YE Z Y, et al. Efficient method for limit cycle flutter analysis by nonlinear aerodynamic reduced-order models[J]. AIAA Journal, 2012, 50(5): 1019-1028.

[12] MANNARINO A, MANTEGAZZA P. Nonlinear aeroelastic reduced order modeling by recurrent neural networks[J]. Journal of Fluids and Structures, 2014, 48: 103-121.

[13] 寇家庆, 张伟伟, 叶正寅. 基于分层思路的动态非线性气动力建模方法[J]. 航空学报, 2015, 36(12): 3785-3797.

KOU J Q, ZHANG W W, YE Z Y. Dynamic nonlinear aerodynamics modeling method based on layered model[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3785-3797 (in Chinese).

[14] KOU J Q, ZHANG W W. An approach to enhance the generalization capability of nonlinear aerodynamic reduced-order models[J]. Aerospace Science and Technology, 2016, 49: 197-208.

[15] ZHANG W W, KOU J Q, WANG Z Y. Nonlinear aerodynamic reduced-order model for limit-cycle oscillation and flutter[J]. AIAA Journal, 2016, 54(10): 3302-3310.

[16] WANG Z C, ZHANG Z C, LEE D H, et al. Flutter analysis with structural uncertainty by using CFD-based aerodynamic ROM[C]//49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2008.

[17] SONG S F, LU Z Z, ZHANG W W, et al. Uncertainty importance measure by fast fourier transform for wing transonic flutter[J]. Journal of Aircraft, 2011, 48(2): 449-455.

[18] MARQUE S, BADCOCK K J, KHODAPARAST H H, et al. Transonic aeroelastic stability predictions under the influence of structural variability[J]. Journal of Aircraft, 2010, 47(4): 1229-1239.

[19] MARQUE S, BADCOCK K J, KHODAPARAST H H, et al. How structural model variability influences transonic aeroelastic stability[J]. Journal of Aircraft, 2012, 49(5): 1189-1199.

[20] ZHANG W W, CHEN K J, YE Z Y. Unsteady aerodynamic reduced-order modeling of an aeroelastic wing using arbitrary mode shapes[J]. Journal of Fluids and Structures, 2015, 58: 254-270.

[21] SCHAIRER E T, HAND L A. Measurements of unsteady aeroelastic model deformation by stereo photogrammetry[J]. Journal of Aircraft, 1999, 36(6): 1033-1040.

[22] GORDNIER R E. Computation of limit-cycle oscillations of a delta wing[J]. Journal of Aircraft, 2003, 40(6): 1206-1208.

(责任编辑： 李明敏)

Unsteady aerodynamic reduced-order modeling method forparameter changeable structure

WANGZiyi,ZHANGWeiwei*

SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China

Computational fluid dynamics (CFD) based unsteady aerodynamic reduced-order model (ROM) can make significant improvement of efficiency of transonic aeroelastic analysis. However, the existing ROM is applicable only to structures with fixed parameters, namely prescribed model shapes (ROM-PMS). When structural parameters should be altered such as structure optimization and uncertainty analysis, ROM-PMS is no longer feasible. To settle the problem, a new unsteady aerodynamic modeling method for arbitrary model shapes is developed based on Ref.[20]. Parametric sampling and modal analysis are conducted on the structure to be designed and analyzed. The basic mode shapes are then obtained through principal component analysis (PCA). Real model shapes of arbitrary structure in the sample space can be synthesized by linearly superimposing basic mode shapes with correct coefficients. The coefficients of superposition change with the alteration of structure parameters. The analysis shows that just small number of basic modes can reach desirable accuracy. Classical modeling method can be used to construct ROM in basic mode shape coordinate. The ROM applicable for various structures can be developed from ROM in basic mode coordinate, which means that structural parameters can be arbitrarily altered in the sample space, while ROM is universal. This method can be widely applied to aeroelastic optimization design and uncertainty analysis, with great improvement in computational efficiency.

structure optimization; parameter variation; reduced-order model (ROM); transonic flow; flutter; unsteady aerodynamics

2016-10-01；Revised2016-11-21；Accepted2017-01-05；Publishedonline2017-01-091550

URL：www.cnki.net/kcms/detail/11.1929.V.20170109.1550.008.html

s：NationalNaturalScienceFoundationforExcellentYoungScholar(11622220);SeedFoundationofInnovationandCreationforGraduateStudentsinNorthwesternPolytechnicalUniversity(z2016002)

2016-10-01；退修日期2016-11-21；录用日期2017-01-05； < class="emphasis_bold">网络出版时间

时间：2017-01-091550

www.cnki.net/kcms/detail/11.1929.V.20170109.1550.008.html

国家自然科学基金优秀青年基金 (11622220)； 西北工业大学研究生创意创新种子基金 (z2016002)

*

.E-mailaeroelastic@nwpu.edu.cn

王梓伊， 张伟伟． 适用于参数可调结构的非定常气动力降阶建模方法J． 航空学报,2017,38(6):220829.WANGZY,ZHANGWW.Unsteadyaerodynamicreduced-ordermodelingmethodforparameterchangeablestructureJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):220829.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.120829

V211.3

A

1000-6893(2017)06-220829-10

*Correspondingauthor.E-mailaeroelastic@nwpu.edu.cn