基于能量最优的敏捷遥感卫星在轨任务规划
2017-11-22赵琳王硕郝勇刘源
赵琳, 王硕, 郝勇, 刘源
哈尔滨工程大学 自动化学院, 哈尔滨 150001
基于能量最优的敏捷遥感卫星在轨任务规划
赵琳, 王硕, 郝勇*, 刘源
哈尔滨工程大学 自动化学院, 哈尔滨 150001
针对敏捷遥感卫星对多个离散观测点在轨自主任务规划问题,在考虑姿态运动方程耦合性的基础上,将问题分解为空间资源调度问题和连续最优控制问题,进而提出了一种结合伪谱法和遗传算法的混合求解算法。该算法针对基于行商问题(TSP)模型建立的空间资源调度问题模型,选用二维编码结构对观测顺序和相对观测时间进行实数编码,并采用遗传算法求解观测序列和观测时间;针对判断观测时间可行性时涉及的时间最优控制问题、以及姿态转移过程中涉及的最小能量消耗问题,将其归结为连续最优控制问题,并基于Gauss伪谱协态变量映射定理,采用Gauss伪谱法进行求解。通过与基于单纯遗传算法的规划算法进行对比试验,本文所提出的基于伪谱法和遗传算法的混合求解策略针对目标问题,在典型工况下姿态转移过程中能量消耗降低60%。
行商问题(TSP); 能量消耗; 时间最优; 遗传算法; Gauss伪谱法
相比于传统的成像卫星,敏捷遥感卫星具有姿态快速机动的能力[1]。基于敏捷遥感卫星的敏捷快速机动能力,敏捷遥感卫星具有更大的观测范围和更强的观测能力。目前成像卫星的运动多是在管控模式下完成的,管控模式是指地面控制系统根据任务需求对卫星的运动状态进行规划并向卫星发射控制指令,但是由于信道占用、通信延迟、时间窗口等限制因素,卫星无法在短时间内对动态的观测任务需求做出响应,因此,针对敏捷遥感卫星敏捷机动的特点,传统的管控模式不能充分发挥敏捷遥感卫星的观测效能。因此为了解决上述问题,基于观测任务需求和卫星自身资源能力的敏捷遥感卫星在轨自主规划是十分必要的[2-4]。
针对敏捷遥感卫星对地观测任务规划问题,Gabrel等[5-6]提出了图论问题模型,将任务规划问题表示成一个加权有向无环图G,并将G的路径作为问题的解,但是对于区域观测或立体观测等复杂约束则无法在该模型中体现;Vasquez和Hao[7]提出背包问题模型,以简单的形式表示任务规划问题的约束,但是该模型不适用于多星任务规划问题;Bensana等[8]提出线性整数规划模型,该模型可以描述所有线性约束,但是不能有效处理非线性约束,且其求解效率随着问题规模的增加而降低;Lemaitre 等[9]提出约束满足问题模型,能有效地处理线性和非线性约束,增强问题描述的完整性,但是该模型的求解效率低;Verfaillie等[10]提出序贯决策模型,采用决策理论处理问题中的不确定因素,但是模型复杂度随着问题约束的增加而增加;贺仁杰[11]提出了具有时间约束的并行机制调度问题模型,将问题中的卫星和观测任务分别映射为机器和工件,并将观测任务的总收益作为调度目标。基于上述模型,在对对地观测任务规划问题进行求解中,Lemaitre等[9]采用动态规划算法对卫星对地观测任务规划问题进行求解,但是当问题规模较大时,其求解时间过长;Xhafa[12]和Wolfe[13]等采用遗传算法(Genetic Algorithm, GA)对问题进行求解并与优先级调度构造算法进行比较,结果表明遗传算法可以大幅度地提高问题求解速度;Cordeau[14]、陈英武[15]和Sarkheyli[16]等采用禁忌搜索算法对问题进行求解,其中,文献[15-16]在采用禁忌算法的同时也考虑了转移时间约束;Wu等[17]采用模拟退火算法将任务目标均假设为点目标,进而对问题进行求解;贺仁杰等[4,11]采用禁忌与列生相结合算法,增强任务规划问题的鲁棒性。
目前,由于卫星上燃料资源的限制,基于能量最优的敏捷遥感卫星在轨自主规划成为研究热点。能量最优问题实质是最优控制问题,针对最优控制问题,刘富钰[18]和Kusuda[19]等根据遗传算法等智能算法对问题进行求解,但是智能算法求出的最优解具有随机性,和真正最优解之间存在误差;张秋华等[20]基于庞德里亚金极小值原理将最优控制问题转换为一个Hamilton边值问题(Hamilton Boundary Value Problem, HBVP),但是利用该算法推导一阶最优条件与横截条件过程繁琐,且对未知条件的初值难以准确估计;文献[21-26]采用伪谱法对最优控制问题进行求解。文献[18,24-25]根据固定时间姿态机动的任务需求,以姿态机动消耗能量最小为优化指标,只考虑了固定起止时间、固定起止姿态一次姿态机动的能量最优控制,因此上述3类最优控制问题的求解方法,对于基于能量最优的敏捷遥感卫星在轨自主规划问题的求解存在局限性。
针对上述局限性,本文基于行商问题(Travelling Salesman Problem, TSP)模型建立了多观测点在轨自主任务规划问题的数学模型,在考虑姿态运动学方程耦合性的基础上,将问题分解为空间资源调度问题和连续最优控制问题,并提出了基于伪谱法和遗传算法的混合求解策略。针对任务层面的空间资源调度问题,采用遗传算法求解;针对规划层面的连续最优控制问题采用Gauss伪谱法求解,进而使得单颗敏捷遥感卫星在固定观测时间区域内实现对多个地面静止离散观测点的完全观测,并且在整个完全观测过程中卫星姿态机动所消耗的能量最小。
1 敏捷遥感卫星任务规划问题描述
1.1 卫星姿态机动的运动方程
1) 基于修正的罗德里格斯参数(Modified Rodrigues Parameters, MRP)的运动方程
卫星姿态动力学方程[27]为
(1)

(2)
采用MRP表示卫星运动姿态为σ,则卫星的非线性运动学方程[28]为
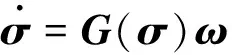
(3)
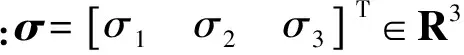

(4)
式中:I3为3×3的单位矩阵。
2) 基于MRP的误差运动方程
σe和ωe分别表示卫星的姿态误差、角速度误差,误差动力学方程和误差运动学方程分别为
(5)
(6)

(7)
1.2 能量最优的多观测点在轨自主任务规划描述
基于能量最优的单颗敏捷遥感卫星对地面多离散观测点进行在轨自主任务规划满足以下几点假设:
1) 卫星运行轨道固定。
2) 地面观测点为离散静止观测点。
3) 完成观测任务的时间区间和起始时间固定。
多观测点任务规划是轨道固定的单颗敏捷遥感卫星在固定时间区域内对多个地面静止观测点实现完全观测的空间资源调度优化问题,其实质是TSP。
TSP的一般性描述为[29]:已知n个城市和n个城市间的距离,一位旅行商要找到一条能够访问所有n个城市,且除第一个被访问的城市外其余每个城市只被访问一次,最终回到第一个城市的路线,并使得该路线的长度最短,或表述为在有n个结点的完全图中找出最短的Hamilton回路。
基于能量最优的单颗敏捷遥感卫星对地面多观测点进行在轨自主任务规划问题描述为:已知n个地面静止观测点,单颗敏捷遥感卫星从规定的起始时间开始以星载相机视轴指向星下点的初始姿态在固定的时间区域内完成对n个地面静止观测点的完全观测,且每个地面静止观测点仅被观测一次,并最终回归星载相机视轴指向星下点的姿态,使得该姿态转移过程中敏捷遥感卫星所消耗的能量最低。
1.3 能量最优的多观测点在轨自主任务规划模型
根据1.2节中能量最优的多观测点在轨自主任务规划描述,基于能量最优的多观测点在轨自主任务规划问题与TSP的映射关系如下:
1) 观测姿态对应TSP中的城市
轨道信息、任务顺序序列中第i个地面静止观测点信息及其对应的观测时间点共同决定了卫星观测任务顺序序列中第i个观测点的姿态,因此卫星观测任务顺序序列中第i个地面静止观测点的姿态可以表示成轨道、地面静止观测点、时间的函数,表达式为
aηi=φ(o,Oηi,Tηi)
(8)
式中:ηi为任务顺序序列的第i个任务;o表示轨道信息;Oηi表示任务顺序序列中第i个地面静止观测点信息;Tηi表示卫星观测任务顺序序列中第i个观测点的时间点;aηi表示卫星观测任务顺序序列中第i个观测点的姿态。
由于轨道在完全观测过程中始终固定,即轨道信息为定值,因此姿态函数可以表示为观测点信息和时间的函数,式(8)可以简化为
aηi=φ(Oηi,Tηi)
(9)
当轨道信息、地面静止观测点及其对应的观测时间点确定时,卫星对应的观测姿态确定,确定的观测姿态a对应TSP中的城市c。映射关系为
a→c
(10)
2) 姿态间机动能耗对应城市间距离
卫星从一个观测姿态到另一个观测姿态机动时所消耗的能量对应城市间距离,映射关系为
E(aηi-1,aηi)→d(cγi-1,cγi)
(11)

(12)
式中:E(aηi-1,aηi)为卫星从观测任务顺序序列中第i-1个观测点的姿态机动到观测任务顺序序列中第i个观测点的姿态所消耗的能量;C=[c1c2…cn](i=1,2,…,n)为TSP中的所有城市;γi为访问城市序列的第i个城市;d(cγi-1,cγi)为城市cγi-1到城市cγi的距离。
将式(9)代入式(11)可得
E(φ(Oηi-1,Tηi-1),φ(Oηi,Tηi))→d(cγi-1,cγi)
(13)
基于上述映射关系,基于能量最优的单颗敏捷遥感卫星对地面多个离散观测点进行在轨自主任务规划的数学模型具体描述如下。
求得一个最优任务顺序序列和时间序列,分别表示为R=[η1η2…ηn]和T=[Tη1Tη2…
Tηn],满足如下目标函数:
φ(Oηi,Tηi))+E(as,φ(Oη1,Tη1))+
E(φ(Oηn,Tηn),at)
(14)
s.t.
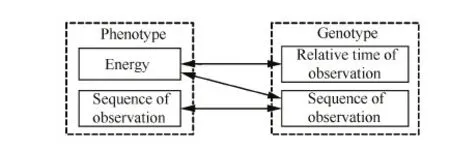
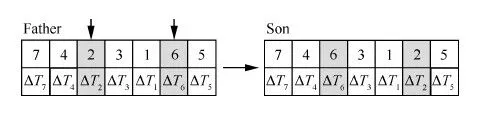
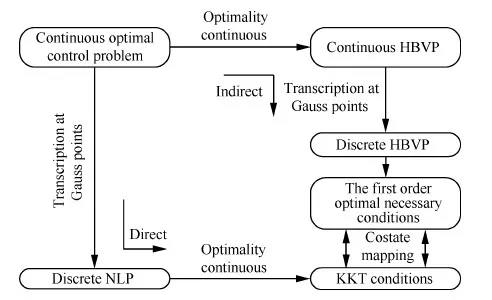
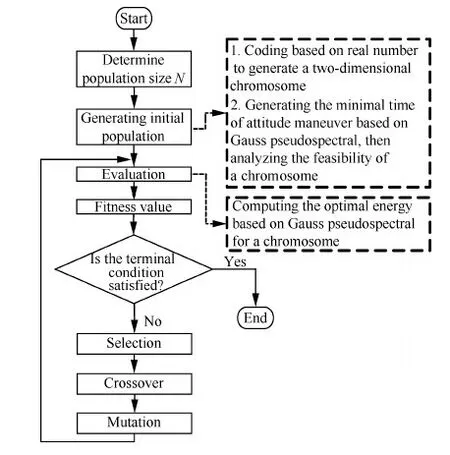
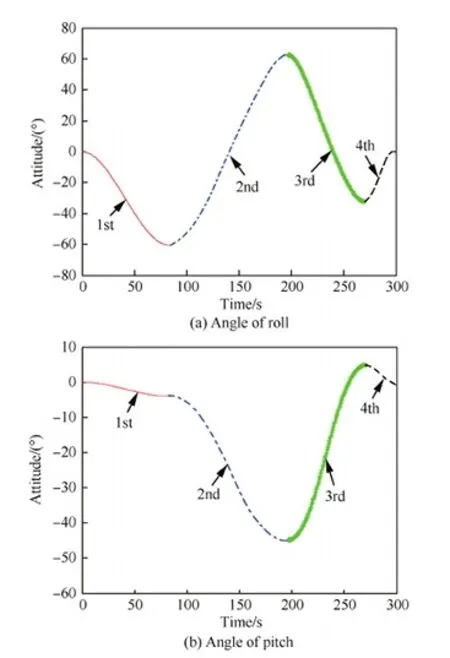
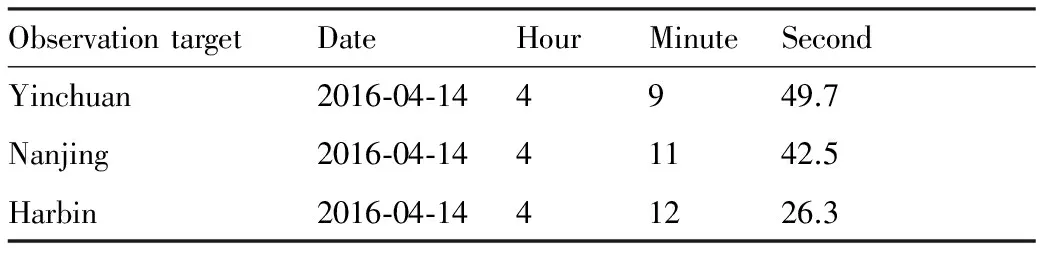
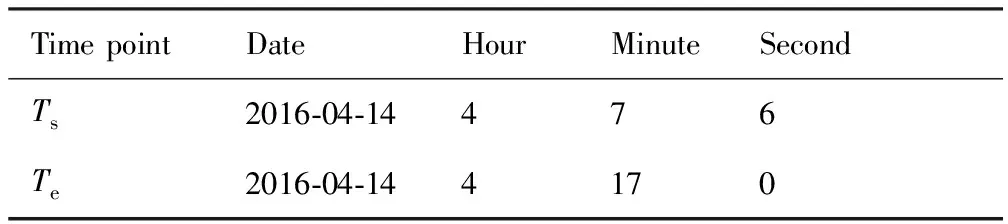
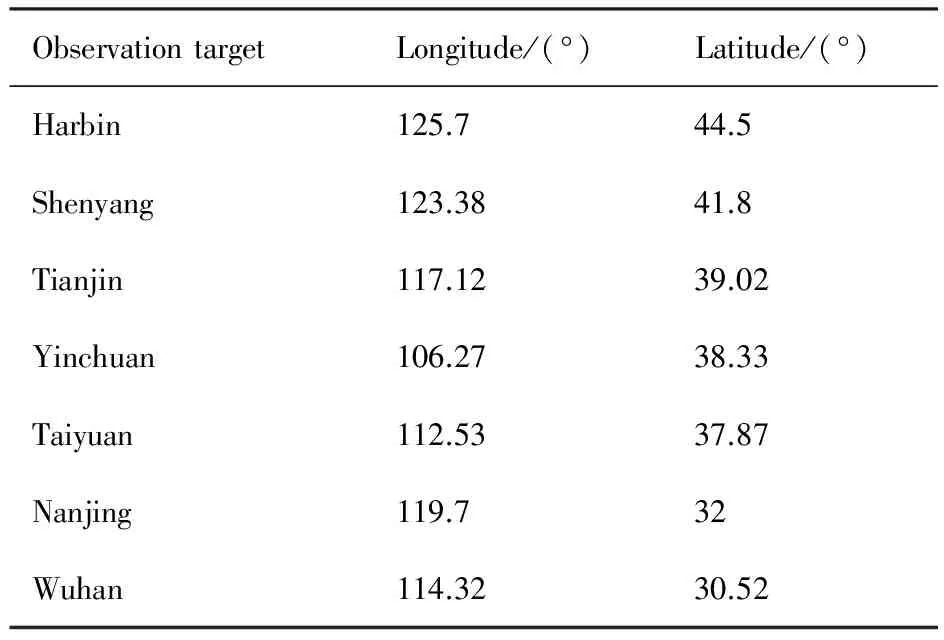
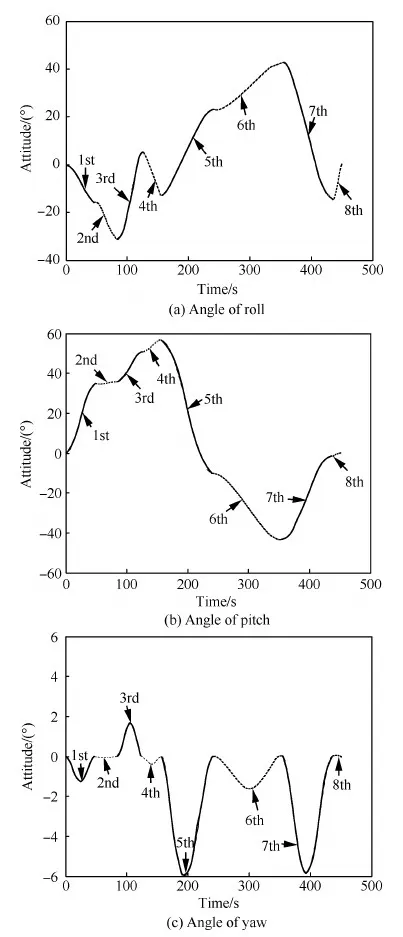
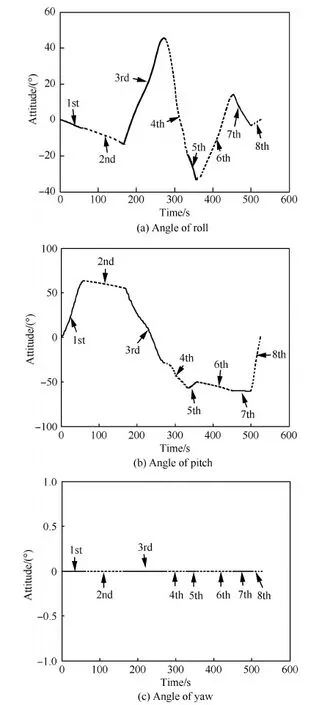
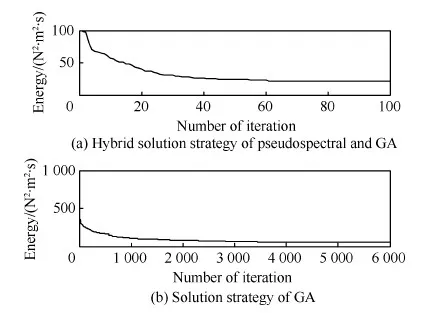
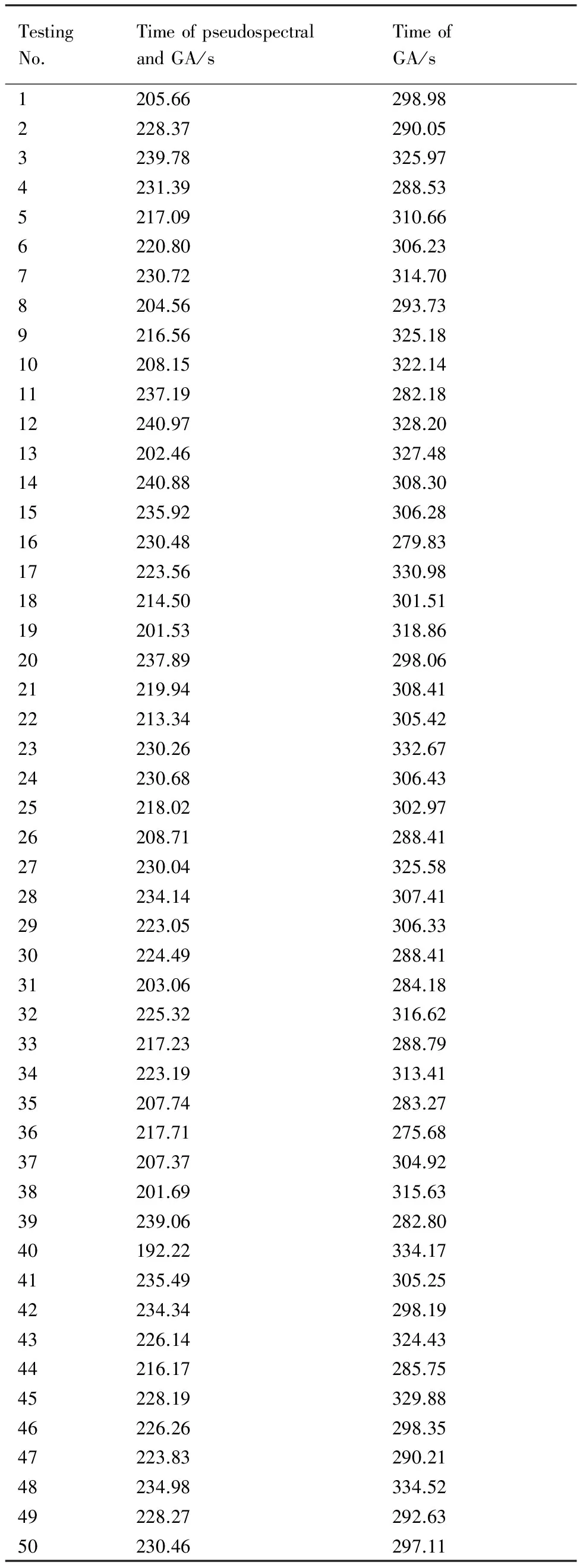
Ts (15) Tt (16) 式中:as为卫星在起始时间星载相机视轴指向星下点的初始姿态;E(as,φ(Oη1,Tη1))为卫星从规定的起始时间开始以星载相机视轴指向星下点的初始姿态机动到卫星观测任务顺序序列中第一个地面静止观测点对应的姿态所消耗的能量;Tt为卫星实现对多地面观测点完全观测的结束时刻;at为卫星在Tt时刻星载相机视轴指向星下点的终止姿态;E(φ(Oηn,Tηn),at)为卫星观测任务顺序序列中最后一个地面静止观测点对应的姿态机动到星载相机视轴指向星下点的终止姿态所消耗的能量;Ts为固定时间区域的起始时间;Te为固定时间区域的终止时间。 TSP是NP(Non-deterministic Polynomial)问题,本文涉及的多观测点在轨自主规划问题同样也属于NP问题。TSP在求解过程中只涉及访问顺序,若设置需要访问的城市数目为n,则所有访问顺序的组合数为(n-1)!/2,其对应的找到最优解的时间复杂度的数量级为O(n!)。而对于多观测点在轨自主任务规划问题,根据其目标函数式(14),可知其求解过程既包括观测顺序又包括观测时间。若设置需要观测的目标数目为n,则所有访问顺序的组合数为(n-1)!/2,所有观测时间的组合为(n-1)!/2,则其对应的找到最优解的时间复杂度的数量级为O((n!)2),可以看出其求得最优解的时间复杂度是传统TSP的n!倍,其求解难度成平方型增长。 针对第1节提出的基于能量最优的多观测点在轨自主任务规划的数学模型,其目标函数是关于时间的函数,因此,轨道固定的单颗敏捷遥感卫星在固定时间区域内对多个地面静止观测点实现完全观测的空间资源调度优化问题是一个具有时间依赖性的调度问题。问题的求解不但与地面静止观测点的观测顺序有关,也依赖于各个地面静止观测点的观测时间,同时需要保证敏捷遥感卫星观测任务顺序序列中相邻两地面静止观测点对应的观测姿态间机动所消耗的能量最小,增加了TSP求解复杂性。文献[4,9,11-17]采用智能算法对任务规划问题进行求解时,对于转换时间约束的处理过于工程化,其转移时间的计算只是考虑了转移姿态与转移平均角速度的线性比,没有考虑卫星实际运行过程中角加速度呈上升和下降趋势分布的实际机理,不能保证转换时间是最优的,进而导致任务规划结果不一定是最优的,因此,为增强任务规划结果的合理性,在处理转换时间约束时,考虑卫星从一个观测姿态机动到另一个观测姿态所需要的最小转移时间,进而为观测地面静止观测点的观测时间点提供更大的选择空间。 综合问题模型的复杂性和转换时间约束计算的合理性,传统的单一智能求解方法已经不能满足该问题的复杂需求,因此,针对该问题的上述特点本文提出了基于伪谱法和遗传算法的混合求解策略,其求解思路如图1所示。 图1 混合求解策略示意图Fig.1 Schematic diagram of hybrid solution strategy 2.1 遗传算法设计 1) 编码方式设计 编码即为解的表现型空间到基因型空间的映射,解码即为解的基因型空间到表现型空间的映射。 敏捷遥感卫星对多个地面静止观测点的观测顺序和敏捷遥感卫星实现完全观测过程中姿态机动所消耗的能量,是基于能量最优的轨道固定的单颗敏捷遥感卫星在固定时间区域内对多个地面静止观测点实现完全观测的空间资源调度优化问题的解。 根据式(13)敏捷遥感卫星姿态机动所耗能量可以表示为地面静止观测点信息和观测时间的函数,而地面静止观测点的选择与敏捷遥感卫星的观测顺序有关,进而敏捷遥感卫星姿态机动所耗能量这一表现型可以映射为敏捷遥感卫星的观测顺序和观测时间这两个基因型。 对每一个地面静止观测点,在不同的任务顺序序列中所处的位置不同,若对其对应的观测时间直接编码,每次经过交叉算子后,将产生大量观测顺序和观测时间相悖的不可行解,降低种群多样性,甚至一次迭代后没有可行解,为解决这一问题,本文采用相对观测时间代替绝对观测时间作为基因型进行编码。表现型到基因型的映射关系如图2所示。 根据上述映射关系,本文基于观测顺序和相对观测时间这两个基因型对问题的解进行编码。若采用一维编码结构对含有两个基因型的解进行编码必然会导致相当数量的信息丢失,因此,本文基于实数编码方式选用二维编码结构对上述两个基因型进行编码,染色体结构如图3所示。图中:ΔTηi为任务顺序序列中第i个观测点相对第i-1个观测点的相对观测时间,当i=1时,ΔTη1为第1个观测点相对卫星初始观测时刻的相对观测时间。 图2 表现型和基因型的映射关系Fig.2 Mapping relationship of phenotype and genotype 图3 染色体结构示意图Fig.3 Schematic diagram of chromosome structure 2) 初始种群生成 设种群大小为N,种群中的每一条染色体代表问题的一个解,根据编码方式,随机生成一条染色体,并判断染色体对应的基因型作为问题的解的可行性,直到生成种群大小的满足可行性的染色体。 染色体观测顺序可行性检验准则为:任务顺序序列中的基因位由1-n范围内的整数随机、无重复排列。 染色体相对观测时间可行性检验准则为:根据式(15),每一条染色体的相对观测时间序列需要满足 Ts (17) 且敏捷遥感卫星观测任务顺序序列中第i个观测点相对第i-1个观测点的相对观测时间需要大于或等于卫星观测任务顺序序列中第i-1个观测点对应的姿态机动到卫星观测第i个观测点对应的姿态所需要的最小转移时间,具体可表示为 min ΔTtrans ηi-1,ηi≤ΔTηi (18) 生成初始种群的步骤为 步骤1随机生成任务顺序序列。 步骤2判断任务顺序序列可行性,若不可行返回步骤1,若可行执行步骤3。 步骤3随机生成相对观测时间序列。 步骤4判断相对观测时间可行性,若不可行返回步骤3,若可行执行步骤5。 步骤5将可行的任务顺序序列和相对观测时间序列作为满足可行性的染色体放入种群中,执行步骤6。 步骤6计算当前种群大小m,并判断m与N的关系,若m=N则执行步骤7,若m 步骤7初始种群生成结束。 3) 适应度函数建立 适应度函数是遗传算法收敛性和稳定性的重要影响因素。由于敏捷遥感卫星的燃料有限,因此姿态机动过程中能量消耗是调度问题寻优的重要影响因素。本文根据单颗敏捷遥感卫星在固定时间区域内对多地面静止观测点实现完全观测所消耗的能量,即式(14)建立适应度函数为 F0=1/f(R,T) (19) 式中:F0为单个染色体的适应度函数值,F0越大,则染色体的能耗函数f(R,T)值越小,卫星在整个调度过程中能量消耗最小,该染色体的性能越好,其适应度越大。 4) 遗传算子设计 本文设计了3个遗传算子,分别是选择算子、交叉算子、变异算子。 选择算子采用精英保留策略和轮盘赌算法。该方法保留每一代种群中染色体适应度函数值最高的,即适应度函数值最高的染色体一定会被选择,保证优秀个体的基因可以遗传到下一代;并根据每个染色体的适应度函数值,计算该染色体在整个种群中被选中的概率和累计概率,其表示为 (20) (21) 式中:Pi为第i个染色体被选中的概率;Qi为第1个染色体到第i个染色体的累计概率。产生一个均匀分布的随机数r∈(0,1),满足Qi-1 针对TSP具有排列性质的编码方式,交叉算子采用部分匹配交叉算法。该方法随机选择两个位置点,这两点之间的基因位作为匹配基因片段,采用位置交换操作交换这两段匹配基因片段的内容,交换匹配基因片段后,若匹配基因片段区域外出现访问重复,则按照匹配基因片段区域内对应的位置映射关系逐一进行交换,直至整条染色体无重复排列,如图4所示。 图4 部分匹配交叉算子Fig.4 Partially matched crossover operators 针对TSP具有排列性质的编码方式,变异算子采用对换变异算法。该方法简单地随机选择两个位置并交换其内容,如图5所示。 当运算经过上述针对具有排列性质的编码方式设计的交叉算子和变异算子后,需要分别对交叉和变异后得到的新的染色体的相对观测时间的可行性进行检验,其步骤为 步骤1根据新染色体的相对观测时间序列和任务顺序序列,计算任务顺序序列中每一个观测点的绝对观测时间,并根据式(15)判断观测序列中最后一个观测点ηn的绝对观测时间Tηn是否满足条件Tηn 图5 点位变异算子Fig.5 Points mutation operator 步骤2根据任务顺序序列和序列中每一个观测点的绝对观测时间,计算序列中每一个观测点的观测姿态,并采用Gauss伪谱法计算两个相邻姿态间的最小转移时间,并根据式(18)判断其是否满足要求,若满足执行步骤5,若不满足执行步骤4。 步骤3重新进行交叉算子或变异算子运算,执行步骤1,若交叉算子或变异算子执行10次后仍没有可行解,则将父代个体作为新的染色体,执行步骤5。 步骤4当不满足式(18)的相对观测时间的个数为1个时,则将该基因位的相对观测时间置换为该基因位父代的相对观测时间,并判断其可行性,若可行执行步骤5,若不可行执行步骤3。当不满足式(18)的相对时间的个数大于或等于2个时,按照扫描交换法交换不满足条件的相对观测时间在相对观测时间序列中的位置,如图6所示。将不可行的相对观测时间从新染色体相对观测时间序列中剔除,并将剔除的不可行相对观测时间加入其他不可行相对观测时间基因位的候选集合中。按照不可行相对观测时间基因位在相对观测时间序列中位置的前后顺序,对该基因位候选集中剩余的相对观测时间候选方案进行随机选取,并判断其可行性。若可行,剔除其后位置中不可行基因位的相对观测时间候选集中与该基因位相同的相对观测时间,然后在其后位置的不可行基因位候选集中进行随机扫描工作,直至新的相对观测时间序列生成,执行步骤5;若不可行,则在该基因位剩余的候选方案中重新进行随机扫描操作,直至挑选到满足条件的方案,执行步骤5。若观测方案候选集都不符合,则执行步骤3。 图6 扫描交换相对观测时间Fig.6 Exchanging relative observation time by scanning 步骤5输出经过交叉算子或变异算子后新的染色体序列,作为新种群的个体。 2.2 基于Gauss伪谱法的最小转移时间生成 针对转换时间约束的处理,传统的处理方法过于工程化,其计算结果较真值存在一定的误差且不具有最优性,本文考虑姿态运动方程耦合性和转移姿态角加速度的呈上升和下降趋势分布的实际机理,采用Gauss伪谱法替代传统的线性方法计算敏捷遥感卫星最小转移时间。敏捷遥感卫星最小转移时间问题,即为敏捷遥感卫星从任务顺序序列中的第i-1个观测点对应的姿态机动到卫星观测第i个观测点对应的姿态所需要的最小转移时间,是一个时间最优控制问题,即卫星从一个姿态跃迁到另一个姿态的过程中满足时间最优性要求,其转移过程如图7所示,图中Sat代表卫星。 敏捷遥感卫星时间最优控制问题可以描述为多约束条件下的连续最优控制问题。连续最优控制问题的一般性描述见文献[30],在此不再赘述。敏捷遥感卫星时间最优控制问题与连续最优控制问题的映射如下: 图7 卫星姿态机动示意图Fig.7 Schematic diagram of satellite attitude maneuver 1) 系统方程 相比于传统的初始状态、终止状态、初始时刻固定、终止时刻不固定的卫星时间最优控制问题[30],本文涉及的卫星时间最优控制问题的初始状态、初始时刻固定,终止时刻、终止状态不固定,是关于时间的函数,其表达式为 xf=ψ(tf) (22) 式中:xf为终止状态;tf为终止时刻。 传统的选用绝对运动方程作为系统方程的方法针对终止状态不固定的时间最优控制问题已经不再适用。为解决上述问题本文选取基于MRP的误差运动方程式(5)、式(6)作为系统方程,进而将问题转化为初始状态为卫星在初始时刻观测第i-1个观测点相对卫星在初始时刻观测第i个观测点的相对姿态,终止状态为零、初始时刻固定、终止时刻不固定的卫星时间最优姿态机动问题。则系统的状态变量为 (23) 2) 约束条件 x(t0)=x0 (24) x(tf)=[0 0 0 0 0 0]T (25) (26) (27) 式中:x0为卫星在t0时刻观测任务顺序序列中的第i-1个观测点对应的姿态相对t0时刻卫星观测任务顺序序列中的第i个观测点对应的姿态的初始误差姿态,t0为定值;x(tf)为卫星在tf时刻的终止误差姿态,tf不是定值;umax为敏捷遥感卫星所配置的执行机构所能提供的最大力矩;ωmax为敏捷遥感卫星机动过程中最大角速度。式(24)、式(25)为边界条件,式(26)、式(27)为路径约束。 3) 性能指标 性能指标Jc的表达式为 (28) 针对具有强耦合性和强非线性系统方程的卫星时间最优控制问题,其解析解是无法求得的。目前求解含有约束条件的最优控制问题的数值解的主要方法包括直接法和间接法。间接法求解最优控制问题主要是基于庞德里亚金极小值原理和变分原理,将最优控制问题转换为一个Hamilton边值问题,进而求得最优控制问题的数值解,但是利用该算法推导一阶最优必要条件与横截条件的过程较为繁琐,且对未知条件的初值和不具有实际物理意义的协态变量的初值难以准确估计,因此,通过间接法求解最优控制问题的数值解十分困难。直接法求解最优控制问题的数值解时不需要求解问题的一阶最优必要条件,而是采用参数化方法将连续的最优控制问题转化为离散的非线性规划(NLP)问题,其收敛域较间接法宽,对初值不敏感。传统的直接法在求解最优控制问题时其求解精度低、收敛速度慢,而Gauss伪谱法可以弥补上述传统直接法的不足,近年来在最优控制问题求解中备受关注[21-26,31-35]。 Gauss伪谱法选择LG(Legendre-Gauss)点作为配点,采用拉格朗日全局插值多项式作为基函数近似状态变量和控制变量在LG点处的值,采用拉格朗日全局插值多项式对时间的导数作为微分方程中状态变量对时间的导数的近似,采用Gauss积分作为性能指标中积分项的近似。 通过Gauss伪谱法的转换可以将连续最优控制问题转化为离散的NLP问题,通过高斯离散化转换的NLP问题满足Benson等[30]提出的高斯伪谱协态变量映射定理:NLP问题的KKT(Karush-Kuhn-Tucker)条件与采用Gauss伪谱法离散化方法离散的连续时间最优控制问题的一阶最优必要条件是完全等价的。其等价关系如图8 所示。 图8 KKT条件与一阶最优必要条件等价性示意图Fig.8 Equivalence schematic of KKT conditions and the first order optimal necessary conditions 上述定理中KKT条件与一阶最优必要条件的等价性证明了基于Gauss伪谱法求得的最优控制问题的解与基于间接法求得的最优控制问题的解的一致性,因此,本文采用基于Gauss伪谱法的直接法求解敏捷遥感卫星时间最优控制问题。求解过程如下: 1) 时间域变换 采用LG点作为配点,则需要做时域变换处理,将优化系统的时间区域t∈[t0,tf]转换为τ∈[-1,1]区间,则时间变量表示为 (29) 2) 基函数选取 选择τ=-1和K个LG点作为节点,其分别为{τ0,τ1,τ2,…,τK},采用拉格朗日全局插值多项式作为基函数,其表达式为 (30) 式中:Li为在第i个点处的拉格朗日全局插值多项式。 3) 状态变量和控制变量近似 基于上述插值近似的基函数,状态变量和控制变量在整个时域的连续函数可由基函数表达,其表达式为 (31) (32) 式中:x(τi)为状态变量在第i个节点的真值,i=0,1,…,K;u(τj)为控制变量在第j个节点的真值,j=1,2,…,K;X(τ)为离散的状态变量;U(τ)为离散的控制变量。 4) 微分方程近似 通过对状态变量函数求导逼近的方法,得到微分方程表达式为 (33) 式中:k=1,2,…,K;Dki为微分矩阵D∈RK×(K+1)中第k行、第i列元素,其定义为 (34) 其中:g(τ)为确定区间上第K个点处的插值基函数,与拉格朗日插值基函数式(30)的关系为 (35) 基于LG点,可将微分方程动态约束转化为代数约束,其表达式为 (36) 式中:F为关于X(τk)、U(τk)和τk的函数。 在选取节点时不包括终端时刻的节点,因此系统的终端状态变量可以通过高斯积分来近似,其表达式为 (37) 式中:wk为高斯积分权重。 5) 性能指标近似 采用Gauss积分作为性能指标中积分项的近似,则性能指标可以表示为 Jc=h(X(tf),tf)+ (38) 式中:h为关于X(tf)和tf的函数;H为关于X(τk)、U(τk)和τk的函数。 基于LG点,边界条件G和路径约束C可以离散为 G(X(t0),t0;X(tf),tf)=0 (39) C(X(τk),U(τk),τk)≤0 (40) 根据上述变换可以将连续最优控制问题离散化为NLP问题。 本文基于MATLAB,采用求解最优控制问题的开源程序GPOPS-II[36]对敏捷遥感卫星时间最优控制问题进行求解。 2.3 基于Gauss伪谱法的能量最优姿态转移路径 敏捷遥感卫星能量最优姿态转移路径生成问题即为敏捷遥感卫星从一个观测姿态机动到另一个观测姿态所需要的最小能量。 为保证姿态间转移能量消耗最小,并考虑姿态运动方程的耦合性,敏捷遥感卫星能量最优姿态转移路径生成问题同样可以描述为多约束条件下的连续最优控制问题。映射关系如下: 1) 系统方程 本文涉及的卫星能量最优姿态转移轨迹生成问题的初始状态、终止状态、初始时刻、终止时刻均固定,选用绝对运动方程式(1)、式(3)作为系统方程,取系统的状态变量为 x=[σTωT]T (41) 2)约束条件 x(t0)=x0 (42) x(tf)=xf (43) (44) (45) 式中:tf为定值。式(42)、式(43)为边界条件,式(44)、式(45)为路径约束。 3) 性能指标 (46) 敏捷遥感卫星能量最优姿态转移路径生成问题求解过程按照2.2节所述,在此不再赘述。 2.4 基于伪谱法和遗传算法的混合求解策略计算 综合2.1~2.3节内容,基于伪谱法和遗传算法的混合求解策略计算流程如图9所示。 图9 基于伪谱法和遗传算法的混合求解策略流程图Fig.9 Flow chart of hybrid solution strategy based on pseudospectral and GA 基于伪谱法和遗传算法的混合求解策略,在遗传运算过程中,针对转移时间约束问题,考虑本文涉及的最优控制问题终止状态不固定的条件,选择基于MRP的误差运动方程,结合误差运动方程的耦合性和Gauss伪谱法解的最优性,采用Gauss伪谱法代替传统的线性方法计算两个相邻姿态间的最小转移时间,进而处理转移时间约束,能够使两相邻姿态间转移角加速度符合上升和下降趋势的实际机理,并为卫星观测地面静止观测点的观测时间提供更大的求解区间。 在对多观测点在轨自主任务规划问题的适应度函数求解中,选择基于MRP的运动方程,同样考虑运动学方程耦合性和Gauss伪谱法解的最优性,采用Gauss伪谱法对两个相邻姿态间的最小能量消耗进行求解。 对于多观测点在轨自主任务规划问题,在求解过程中,每一条染色体的表现型不相同,即任务顺序序列和绝对观测时间序列都不相同,且每次迭代后新生成的可行染色体的表现型与其父代个体不同。根据式(9),任务顺序序列和绝对观测时间序列的不同决定了观测姿态序列不同,且观测姿态序列在每次迭代过程中都是高动态变化的,若采用传统的单一遗传算法进行求解,对于嵌套了姿态间时间最优控制问题和最小能量消耗问题的多观测点在轨自主任务规划问题,其编码方式较为复杂,且求得的结果精度不一定满足最优性要求;而采用结合Gauss伪谱法和遗传算法的混合求解算法,可以通过高斯伪谱协态变量映射定理证明,在观测姿态序列高动态变化条件下,该算法可以对姿态间时间最优控制问题和姿态间能量最优问题求得最优解,进而降低了对遗传算法编码方式的要求,提高了计算精度。 3.1 仿真条件与优化结果 1) 仿真参数设置 本文以MATLAB 2014b为实验平台,采用CPU为3.40 GHz/i3-3240,内存为4.0 G,操作系统为Windows 7的计算机做优化计算。基于能量最优的敏捷遥感卫星对多个离散观测点在轨自主任务规划问题的参数设置为:地球半径为6 378.136 55 km,地球曲率半径为 1.0/298.257 22,地球引力常数为398 600.44 km3/s2。 敏捷遥感卫星的转动惯量为[200 0 0;0 200 0;0 0 200] kg·m2,其配置的执行机构所能提供的最大控制力矩为125 N·m,卫星机动过程中所能达到的最大角速度为0.2 rad/s。卫星从一个姿态机动到另一个姿态时的初始和终止角速度和角加速度分别为[0 0 0]Trad/s、[0 0 0]Trad/s2。 采用本文提出的基于伪谱法和遗传算法混合求解策略,求解第1节所描述的能量最优的多观测点在轨自主任务规划问题时,遗传参数设置为:种群规模为50,迭代次数为100;交叉概率为 0.7,变异概率为0.01。 Raja等[37]以能量最优为目标函数,采用遗传算法对运动轨迹进行优化。本文基于文献[37]所提单纯遗传算法方法对第1节所描述的能量最优的多观测点在轨自主任务规划问题进行求解,并与本文提出算法的优化结果进行对比。其仿真参数设置为:种群规模为50,迭代次数为5 000;对观测顺序和观测时间进行交叉和变异操作时,其交叉概率和变异概率分别为0.7和0.01;对姿态路径规划时,其交叉概率和变异概率分别为0.8和0.05。 2) 仿真结果 对3个离散静止观测点的简单成像任务进行规划,初始轨道对应的时刻为2016年4月14日0时0分0秒,初始轨道参数、卫星观测时间区间、观测目标参数如表1~表3所示。表1中:a表示轨道半长轴;e表示轨道偏心率;i表示轨道倾角;Ω表示升交点赤径;W表示近地点幅角;M表示平近点角。 基于伪谱法和遗传算法的混合求解策略得到的仿真结果如表4、图10所示。实现轨道固定的单颗敏捷遥感卫星在固定时间区域内对3个地面静止观测点的完全观测所消耗能量为14.599 6 N2·m2·s。 表1 简单任务初始轨道参数Table 1 Initial parameters of orbit for simple misson 表2 简单任务观测时间窗Table 2 Time window of observation for simple misson 表3简单任务观测目标信息 Table3Informationofobservationtargetforsimplemisson ObservationtargetLongitude/(°)Latitude/(°)Nanjing119.732Yinchuan106.2738.33Harbin125.744.5 表4基于混合求解策略的简单任务观测顺序和时间 Table4Sequenceandtimeofobservationbasedonhybridsolutionstrategyforsimplemission ObservationtargetDateHourMinuteSecondNanjing2016⁃04⁃144101.8Yinchuan2016⁃04⁃1441156.2Harbin2016⁃04⁃1441310.1 图10 基于混合求解策略的简单任务姿态机动路径 Fig.10 Path of attitude maneuver based on hybrid solution strategy for simple misson 基于文献[37]中所提单纯遗传算法求解得到的仿真结果如表5、图11所示。实现轨道固定的单颗敏捷遥感卫星在固定时间区域内对3个地面静止观测点的完全观测所消耗能量为34.336 8 N2·m2·s。且两种算法迭代过程如图12所示。 在其他仿真参数保持不变的前提下,考虑对7个离散静止观测点的复杂成像任务进行规划,其中,初始轨道的时刻为2016年4月14日0时0分0秒,初始轨道参数、观测时间窗、观测目标信息如表6~表8所示。 表5基于遗传算法的简单任务观测顺序和时间 Table5SequenceandtimeofobservationbasedonGAforsimplemisson ObservationtargetDateHourMinuteSecondYinchuan2016⁃04⁃144949.7Nanjing2016⁃04⁃1441142.5Harbin2016⁃04⁃1441226.3 图11 基于遗传算法的简单任务姿态机动路径 Fig.11 Path of attitude maneuver based on GA for simple misson 图12 简单任务的两种算法迭代过程Fig.12 Iterative processes of two algorithms for simple mission 表6 复杂任务初始轨道参数Table 6 Initial parameters of orbit for complex mission 基于伪谱法和遗传算法的混合求解策略得到的仿真结果如表9、图13所示。实现轨道固定的单颗敏捷遥感卫星在固定时间区域内对7个地面静止观测点的完全观测所消耗能量为21.576 0 N2·m2·s。 基于文献[37]中所提单纯遗传算法求解得到的仿真结果如表10、图14所示。实现轨道固定的单颗敏捷遥感卫星在固定时间区域内对7个地面静止观测点的完全观测所消耗能量为52.842 2 N2·m2·s。两种算法迭代过程如图15所示。 表7 复杂任务观测时间窗Table 7 Time window of observation for complex mission 表8复杂任务观测目标信息 Table8Informationofobservationtargetforcomplexmission ObservationtargetLongitude/(°)Latitude/(°)Harbin125.744.5Shenyang123.3841.8Tianjin117.1239.02Yinchuan106.2738.33Taiyuan112.5337.87Nanjing119.732Wuhan114.3230.52 表9基于混合求解策略的复杂任务观测顺序和时间 Table9Sequenceandtimeofobservationbasedonhybridsolutionstrategyforcomplexmission ObservationtargetDateHourMinuteSecondWuhan2016⁃04⁃144827.93Nanjing2016⁃04⁃14494.59Tianjin2016⁃04⁃144944.99Shenyang2016⁃04⁃1441016.18Taiyuan2016⁃04⁃1441141.18Yinchuan2016⁃04⁃1441334.12Harbin2016⁃04⁃1441455.96 图13 基于混合求解策略的复杂任务姿态机动路径 Fig.13 Path of attitude maneuver based on hybrid solution strategy for complex mission 表10基于遗传算法的复杂任务观测顺序和时间 Table10SequenceandtimeofobservationbasedonGAforcomplexmission ObservationtargetDateHourMinuteSecondHarbin2016⁃04⁃144841.32Shenyang2016⁃04⁃1441032.24Yinchuan2016⁃04⁃1441221.33Wuhan2016⁃04⁃1441325.39Nanjing2016⁃04⁃1441348.41Taiyuan2016⁃04⁃1441528.32Tianjin2016⁃04⁃1441615.23 图14 基于遗传算法的复杂任务姿态机动路径Fig.14 Path of attitude maneuver based on GA for complex mission 3) 能量消耗 针对3个离散静止观测点(3个城市)的简单成像任务规划问题和7个离散静止观测点(7个城市)的复杂成像任务规划问题,采用基于伪谱法和遗传算法的混合求解算法与单纯遗传算法分别进行了50次测试,计算两个算法50次仿真输出结果中的能量值,并做平均值处理,计算结果如图16 所示。 图15 复杂任务的两种算法迭代过程 Fig.15 Iterative processes of two algorithms for complex mission 图16 两种算法能量消耗Fig.16 Energy consumption of two algorithms 4) 仿真时间 针对3个离散静止观测点的简单成像任务规划问题和7个离散静止观测点的复杂成像任务规划问题,采用两种算法分别进行了50次测试,并得到50次测试的仿真时间见表11和表12所示。 表11 简单任务仿真时间Table 11 Time of simulation for simple mission 表12 复杂任务仿真时间Table 12 Time of simulation for complex mission 针对3个离散静止观测点的成像任务规划问题,基于伪谱法和遗传算法的混合求解策略求解的平均仿真时间为222.41 s,基于单纯遗传算法求解的平均仿真时间为305.71 s。 针对7个离散静止观测点的成像任务规划问题,基于伪谱法和遗传算法的混合求解策略求解的平均仿真时间为483.06 s,基于单纯遗传算法求解的平均仿真时间为680.56 s。 3.2 结果分析 根据图10、图11和图13、图14,分别对比两组算例中两种优化算法得到的姿态路径转移轨迹,其中,基于伪谱法和遗传算法的混合求解策略规划得到的姿态路径转移轨迹明显较为平滑,避免了单纯遗传算法中编码点数随机性造成的求解结果中姿态路径转移轨迹抖动的现象,进而降低实现完全观测姿态转移所消耗的能量。且根据图12、图15和仿真结果,基于伪谱法和遗传算法的混合求解策略实现轨道固定的单颗敏捷遥感卫星在固定时间区域内对多个地面静止观测点的完全观测所消耗能量小于基于遗传算法的求解策略实现完全观测所消耗的能量,进一步验证了上述结论。 进一步对比两组算例中两种优化算法得到的姿态路径转移轨迹,在偏航轴上两组仿真曲线差别较大,基于伪谱法和遗传算法的混合求解策略考虑了卫星运动方程的耦合性,当偏航轴的起始和终止姿态相同、起始和终止角速度相同时,偏航轴姿态路径会发生姿态转移现象,而在采用单纯遗传算法对姿态转移路径进行规划时,没有考虑卫星姿态运动方程的耦合性,当偏航轴的起始和终止姿态相同、起始和终止角速度相同时,偏航轴姿态路径不会有姿态转移过程。 根据图12和图15,从两个算例中两种算法迭代过程可以看出,基于伪谱法和遗传算法的混合求解策略的求解过程迭代次数小,优化时间较短;基于单纯遗传算法的求解策略的求解过程迭代次数高,需要几千次甚至上万次迭代,其优化时间长,求解效率低。根据表11和表12,通过分别对两个算例采用两种算法进行50次测试,得到50次测试仿真时间的平均值可以看出,基于伪谱法和遗传算法的混合求解策略平均仿真时间小于单纯遗传算法的平均仿真时间。通过仿真曲线和仿真结果可以看到,基于伪谱法和遗传算法的混合求解策略优于基于遗传算法的求解策略,且其求解效率明显高于基于遗传算法的求解策略。 根据图16(a),对于3个离散静止观测点的简单成像任务进行规划问题,采用基于伪谱法和遗传算法的混合求解策略得到的平均能量约为13.349 7 N2·m2·s,采用单纯遗传算法得到的平均能量约为32.976 9 N2·m2·s,采用混合求解策略在姿态转移过程中能量消耗降低约为60%;根据图16(b),对于7个离散静止观测点的复杂成像任务规划问题,采用基于伪谱法和遗传算法的混合求解策略得到的平均能量约为21.123 3 N2·m2·s,采用单纯遗传算法得到的平均能量约为53.576 0 N2·m2·s,采用混合求解策略在姿态转移过程中能量消耗降低约为60%。因此,综合上述两个算例的仿真结果,采用基于伪谱法和遗传算法的混合求解策略在姿态转移过程中能量消耗相对于采用单纯遗传算法的能量消耗降低约为60%。 根据上述仿真结果分析,采用结合Gauss伪谱法和遗传算法的混合求解算法的优势如下: 1) 避免了单纯遗传算法中编码点数随机性造成的求解结果中姿态路径转移轨迹抖动的现象,进而降低实现完全观测姿态转移所消耗的能量; 2) 该混合求解策略考虑了卫星运动方程的耦合性,当偏航轴的起始和终止姿态相同、起始和终止角速度相同时,偏航轴姿态路径会发生姿态转移现象,更加符合卫星实际的运动特性; 3) 该混合求解策略在每次迭代过程中观测姿态序列高动态变化条件下,可以对姿态间时间最优控制问题和姿态间能量最优问题求得最优解,避免单纯遗传算法求解嵌套了姿态间时间最优控制问题和姿态间最小能量消耗问题的多观测点在轨自主任务规划问题时其编码方式较为复杂的情况,降低了对遗传算法编码方式的要求,提高计算精度以及求解效率。 1) 本文解决了敏捷遥感卫星对多个离散观测点观测的在轨自主任务规划问题。即在固定时间区域内实现对地面多个离散观测点的完全观测。 2) 在考虑姿态运动方程耦合性的基础上,以能量最优为目标函数,将问题分解为任务层面的空间资源调度问题和规划层面的连续最优控制问题,提出了一种结合伪谱法和遗传算法的混合求解算法。对任务层选用二维编码结构对观测顺序和相对观测时间进行实数编码,并采用遗传算法求解观测序列和观测时间;对时间最优控制问题、规划层的最小能量消耗问题这两个连续最优控制问题,基于Benson提的Gauss伪谱协态变量映射定理,采用Gauss伪谱法进行求解。 3) 与单纯遗传算法的仿真对比实验验证了本文算法的高效性。该方法规划出的姿态路径转移曲线更加平滑,有效降低了单纯遗传算法编码点数随机性造成的曲线抖动性,进而降低了实现完全观测姿态转移所消耗的能量,在典型工况下,经过多次仿真实验,姿态转移过程中能量消耗降低约为60%。 [1] 廉振宇, 谭跃进, 严珍珍. 敏捷卫星调度的时间约束推理方法[J]. 系统工程与电子技术, 2013, 35(6):1206-1211. LIAN Z Y, TAN Y J, YAN Z Z. Temporal reasoning technology for AEOS scheduling[J]. Systems Engineering and Electronics, 2013, 35(6): 1206-1211 (in Chinese). [2] BEAUMET G, VERFAILLIE G, CHARMEAU M C. Feasibility of autonomous decision making on board an agile earth-observing satellite[J]. Computational Intelligence, 2011, 27(1): 123-139. [3] XU R, CHEN H P, LIANG X L, et al. Priority-based constructive algorithms for scheduling agile earth observation satellites with total priority maximization[J]. Expert Systems with Applications, 2016, 51: 195-206. [4] 贺仁杰, 高鹏, 白保存, 等. 成像卫星任务规划模型、算法及其应用[J]. 系统工程理论与实践, 2011, 31(3): 411-422. HE R J, GAO P, BAI B C, et al. Models, algorithms and applications to the mission planning system of imaging satellites[J]. Systems Engineering-Theory & Practice, 2011, 31(3): 411-422 (in Chinese). [5] GABREL V, VANDERPOOTEN D. Enumeration and interactive selection of efficient paths in a multiple criteria graph for scheduling an earth observing satellite[J]. European Journal of Operational Research, 2002, 139(3): 533-542. [6] GABREL V, MOULET A, MURAT C, et al. A new single model and derived algorithms for the satellite shot planning problem using graph theory concepts[J]. Annals of Operational Research, 1997, 69(1): 115-134. [7] VASQUEZ M, HAO J K. A “logic-constrained” knapsack formulation and a tabu algorithm for the daily photograph scheduling of an earth observing satellite[J]. Computational Optimization and Applications, 2001, 20(2): 137-157. [8] BENSANA E, LEMAITRE M, VERFAILLIE G. Earth observation satellite management[J]. Constraints, 1999, 4(3): 293-299. [9] LEMAITRE M, VERFAILLIE G, JOUHAUD F, et al. Selecting and scheduling observations of agile satellites[J]. Aerospace Science and Technology, 2002, 6(5): 367-381. [10] VERFAILLIE G, LEMAITRE M, SCHIEX T. Russian doll search for solving constraint optimization problems[C]//Proceedings of the 13th National Conference on Artificial Intelligence. Palo Alto: AAAI, 1996: 181-187. [11] 贺仁杰. 成像侦察卫星调度问题研究[D]. 长沙: 国防科学技术大学, 2004: 15-23. HE R J. Research on imaging reconnaissance satellite scheduling problem[D]. Changsha: National University of Defense Technology, 2004: 15-23 (in Chinese). [12] XHAFA F, SUN J Z, BAROLLI A, et al. Genetic algorithms for satellite scheduling problems[J]. Mobile Information System, 2012, 8(4): 351-377. [13] WOLFE W, SORENSEN S E. Three scheduling algorithms applied to earth observing systems domain[J]. Management Science, 2000, 46(1): 148-166. [14] CORDEAU J-F, LAPORTE G. Maximizing the value of an Earth observation satellite orbit[J]. Journal of the Operational Research Society, 2005, 56(8): 962-968. [15] 陈英武, 方炎申, 李菊芳, 等. 卫星任务调度问题的约束规划模型[J]. 国防科技大学学报, 2006, 28(5): 126-132. CHEN Y W, FANG Y S, LI J F, et al. Constraint programming model of satellite mission scheduling[J]. Journal of National University of Defense Technology, 2006, 28(5): 126-132 (in Chinese). [16] SARKHEYLI A, BAGHERI A, GHORBANI-VAGHEI B, et al. Using an effective tabu search in interactive resource scheduling problem for LEO satellites missions[J]. Aerospace Science and Technology, 2013, 29(1): 287-295. [17] WU G H, LIU J, MA M H, et al. A two-phase scheduling method with the consideration of task clustering for earth observing satellites[J]. Computers & Operations Research, 2013, 40(7): 1884-1894. [18] 刘富钰, 崔培玲. 基于改进遗传算法的敏捷卫星姿态路径规划[J]. 电光与控制, 2012, 19(12): 23-33. LIU F Y, CUI P L. Attitude path planning for agile satellite based on improved genetic algorithm[J]. Electronics Optics & Control, 2012, 19(12): 23-33 (in Chinese). [19] KUSUDA Y, TAKAHASHI M. Feedback control with nominal inputs for agile satellites using control moment gyros[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(4): 1209-1218. [20] 张秋华, 孙松涛, 谌颖, 等. 时间固定的两航天器追逃策略及数值求解[J]. 宇航学报, 2014,35(5): 537-544. ZHANG Q H, SUN S T, CHEN Y, et al. Strategy and numerical solution of pursuit-evasion with fixed duration for two spacecraft[J]. Journal of Astronautics, 2014, 35(5): 537-544 (in Chinese). [21] SPILLER D, ANSALONE L, CURTI F. Particle swarm optimization for time-optimal spacecraft reorientation with keep-out cones[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(2): 312-325. [22] 刘刚, 李传江, 马广富, 等. 应用SGCMG的卫星姿态快速机动控制[J]. 航空学报, 2011, 32(10): 1905-1913. LIU G, LI C J, MA G F, et al. Time efficient controller design for satellite attitude maneuvers using SGCMG[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10): 1905-1913 (in Chinese). [23] LI J, XI X N. Time-optimal reorientation of the rigid spacecraft using a pseudospectral method integrated homotopic approach[J]. Optimal Control Application & Methods, 2015, 36(6): 889-918. [24] 丰志伟, 张永合, 刘志超, 等. 基于路径规划的敏捷卫星姿态机动反馈控制方法[J]. 国防科技大学学报, 2013, 35(4):1-6. FENG Z W, ZHANG Y H, LIU Z C, et al. Feedback control method for attitude maneuver of agile satellite based on trajectory optimization[J]. Journal of National University of Defense Technology, 2013, 35(4): 1-6 (in Chinese). [25] GUO T D, JIANG F H, BAOYIN H X, et al. Fuel optimal low thrust rendezvous with outer planets via gravity assist[J]. Science China Physics, Mechanics & Astronomy, 2011, 54(4): 756-769. [26] GARG D, PATTERSON M A, FRANCOLIN C, et al. Direct trajectory optimization and costate estimation of finite-horizon and infinite-horizon optimal control problems using a Radau pseudospectral method[J]. Computational Optimization and Applications, 2011, 49(2): 335-358. [27] 黄静. 三轴稳定航天器姿态最优控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2010: 15-16. HUANG J. Optimal attitude control for three-axis stabilized spacecrafts[D]. Harbin: Harbin Institute of Technology, 2010: 15-16 (in Chinese). [28] TSIOTRAS P. Stabilization and optimality results for the attitude control problem[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(4): 772-779. [29] LIN W, DELGADO-FRIAS J G, GAUSE D C, et al. Hybrid Newton-Raphson genetic algorithm for the travelling salesman problem[J]. Cybernetics and Systems, 1995, 26(4): 387-412. [30] BENSON D A, HUNTINGTON G T, THORVALDSEN T P, et al. Direct trajectory optimization and costate estimation via an orthogonal collocation method[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(6): 1435-1440. [31] 叶东. 敏捷卫星姿态快速机动与稳定控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 15-19. YE D. Research on fast maneuver and stabilization control for agile satellite[D]. Harbin: Harbin Institute of Technology, 2013: 15-19 (in Chinese). [32] 呼卫军, 卢青, 常晶, 等. 特征趋势分区Gauss伪谱法解再入轨迹规划问题[J]. 航空学报, 2015, 36(10): 3338-3348. HU W J, LU Q, CHANG J, et al. Reentry trajectory planning method based on Gauss pseudospectral with character istics of trend partition[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3338-3348 (in Chinese). [33] 张煜, 张万鹏, 陈璟, 等. 基于Gauss伪谱法的UCAV对地攻击武器投放轨迹规划[J]. 航空学报, 2011, 32(7): 1240-1251. ZHNAG Y, ZHANG W P, CHEN J, et al. Air-to-ground weapon delivery trajectory planning for UCAVs using Gauss pseudospectral method[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(7): 1240-1251 (in Chinese). [34] 白瑞光, 孙鑫, 陈秋双, 等. 基于Gauss伪谱法的对UAV协同航迹规划[J]. 宇航学报, 2014, 35(9): 1022-1029. BAI R G, SUN X, CHEN Q S, et al. Multiple UAV cooperative trajectory planning based on Gauss pseudospectral method[J]. Journal of Astronautics, 2014, 35(9): 1022-1029 (in Chinese). [35] GUO T D, JIANG F H, LI J F. Homotopic approach and pseudospectral method applied jointly to low thrust trajectory optimization[J]. Acta Astronautica, 2012, 71: 38-50. [36] PATTERSON M A, RAO A V. GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive gaussian quadrature collocation methods and sparse nonlinear programming[J]. ACM Transactions on Mathematical Software, 2014, 41(1): 1-37. [37] RAJA R, DUTTA A, VENKATESH K S. New potential field method for rough terrain path planning using genetic algorithm for a 6-wheel rover[J]. Robotics and Autonomous Systems, 2015, 72: 295-306. (责任编辑: 张玉, 王娇) Energy-optimal in orbit mission planning for agile remotesensing satellites ZHAOLin,WANGShuo,HAOYong*,LIUYuan CollegeofAutomation,HarbinEngineeringUniversity,Harbin150001,China A new hybrid algorithm combining pseudospectral method and genetic algorithm is presented in this work to solve the in orbit autonomous mission planning problem for the agile remote sensing satellite at multiple discrete observation points. The problem is broken into space resource scheduling problem and continuous optimal control problem based on the coupling of attitude motion equations. This algorithm, according to the space resource scheduling model built based on the travelling salesman problem (TSP) model, encodes the observation sequence and the relative observation time by a two-dimensional real coding structure, and calculates the observation sequence and the observation time by the genetic algorithm. The time optimal control problem in judging the observation time feasibility and the minimal energy consumption in attitude maneuvering are considered as the continuous optimal control problem, which is then solved by Gauss pseudospectral method based on Gauss pseudospectral costate mapping theorem. A comparative simulation test is carried out for the simple genetic algorithm and the proposed algorithm. The simulation results show that the energy consumption obtained by the proposed algorithm is reduced by 60% compared with that obtained by the simple genetic algorithm under typical simulation conditions. travelling salesman problem (TSP); energy consumption; time optimal; genetic algorithm; Gauss pseudospectral method 2016-07-28;Revised2016-09-07;Accepted2016-11-14;Publishedonline2016-11-211439 URL:www.cnki.net/kcms/detail/11.1929.V.20161121.1439.010.html s:NationalNaturalScienceFoundationofChina(61273081);PostdoctoralScientificResearchDevelopmentalFundofHeilongjiangProvinceofChina(LBH-Q14054);theFundamentalResearchFundsfortheCentralUniversitiesofChina(HEUCFD1503) 2016-07-28;退修日期2016-09-07;录用日期2016-11-14; < class="emphasis_bold">网络出版时间 时间:2016-11-211439 www.cnki.net/kcms/detail/11.1929.V.20161121.1439.010.html 国家自然科学基金 (61273081); 黑龙江省博士后科研启动金 (LBH-Q14054);中央高校基本科研业务费专项资金 (HEUCFD1503) * .E-mailhaoyong@hrbeu.edu.cn 赵琳, 王硕, 郝勇, 等. 基于能量最优的敏捷遥感卫星在轨任务规划J. 航空学报,2017,38(6):320654.ZHAOL,WANGS,HAOY,etal.Energy-optimalinorbitmissionplanningforagileremotesensingsatellitesJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):320654. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2016.0298 V249.122 A 1000-6893(2017)06-320654-19 *Correspondingauthor.E-mailhaoyong@hrbeu.edu.cn2 基于伪谱法和遗传算法的混合求解策略






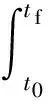
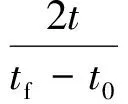
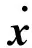



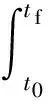
3 仿真验证与结果分析
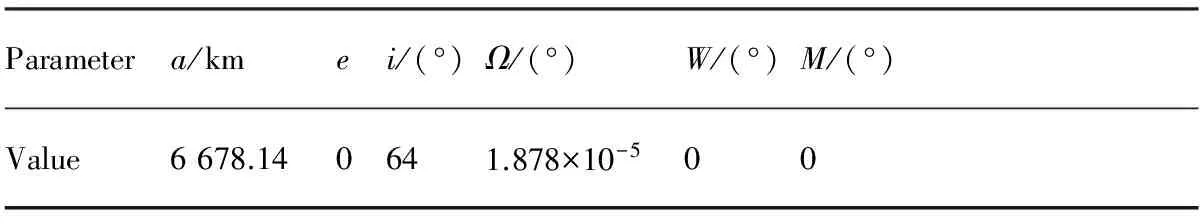












4 结 论
