基于离散元的西北旱区农田土壤颗粒接触模型和参数标定

石林榕，赵武云，孙 伟



基于离散元的西北旱区农田土壤颗粒接触模型和参数标定

石林榕，赵武云※，孙 伟

（甘肃农业大学机电工程学院，兰州 730070）

为了解决利用离散元法模拟土壤作业过程在预测农具阻力和土壤动态运动时存在失真等问题，整合延迟弹性模型（hysteretic spring contact model，HSCM）和线性内聚力模型（liner cohesion model，LCM）优势建立西北旱区农田土壤模型，以不同参数（静摩擦系数、动摩擦系数和内聚强度）组合下仿真得到的土壤仿真堆积角为响应值，基于Box-Behnken试验法建立回归模型，并根据该回归模型进行了参数预测并验证，对17组土壤仿真堆积角方差分析表明：静摩擦系数、动摩擦系数、动摩擦系数和抗剪强度的交互项、动摩擦系数的二次项对仿真堆积角的影响极显著；静摩擦系数和动摩擦系数的交互项、静摩擦系数的二次项对仿真堆积角的影响显著。使用预测的参数进行6种不同含水率土壤直接剪切仿真和试验对比可知，当含水率为1%～20%时，仿真与试验间的抗剪强度相对误差为1.18%～9.31%，仿真与试验间的内摩擦角相对误差为0.55%～4.07%。对仿真和试验鸭嘴插入阻力数据进行分析可知，仿真与试验曲线在入土距离处于0～50 mm期间时，但仿真入土阻力曲线波动较大，仿真和试验阻力走势基本一致，玉米直插穴播最深处50 mm处的仿真和试验入土阻力相对误差为0.928%，可利用此时的入土阻力分析直插鸭嘴结构对强度的影响。

土壤；离散元法；摩擦系数；参数；标定

0 引 言

在农业精耕细作、精密播种、高效收获等作业过程及减阻降耗研究中，土壤力学是设计和优化触土部件优先研究的问题[1-2]。多种方法已经用于研究农具－土壤互相作用过程的研究。传统经验方法在分析土壤运动行为时只涉及土壤应力失效问题[3]。Asaf等[4]提出的基于Terzaghi’s被动土壤压力理论的数值模拟方法--离散元法（discrete element method，DEM）和流体动力学（computational fluid dynamics，CFD）不仅可以计算模型作业阻力，还能模拟土壤破碎过程，但FEM和CFD只能对连续介质的土壤进行整体分析[5]。农田作业过程中存在土层的分离、混合和裂缝及土壤颗粒的流动，呈现出散粒体的特性，DEM可为研究土壤复杂的动态行为提供了新的思路和方法。

内摩擦力、内聚力和黏附力是影响田间作业阻力的关键土壤参数。内摩擦力是土颗粒滑动特性之一。内聚力为相邻颗粒间粘结的分子力，由土颗粒间存在的液桥引起。黏附力为不同材料互相吸附的分子力。现有基于DEM研究土壤文献大体分为3类[6]：1）土颗粒间的液桥形成的内聚力和黏附力，介于其方程的复杂性及颗粒的不规则，目前还未应用于土壤-农具互作仿真模型；2）基于宏观物理力学定律建立的涉及内聚力和黏附力土壤模型，通过匹配试验结果进行参数校准，其中并行黏结模型（parallel bond contact model，PBCM）多被用于建立具有内聚力的土壤-农具仿真模型[7]，PBCM模型中颗粒间由粘结键连接来限制颗粒法向和切向力，当法向和切向力大于预先设定的力值，粘结键会被删除，其后颗粒间通过Hertz-Mindlin模型（Hertz Mindlin contact model）进行计算。石林榕等[8]借助Flunet-UDF将土壤单轴压缩有限元模型网格信息导出，利用PBCM生成含水率为10.5%的不饱和土壤单轴压缩模型，仿真结果显示模型轴向压缩力-应变曲线与试验曲线基本一致。然而HMCM模型在预测土壤-农具互作模型时会产生不真实的垂直阻力[9-10]；3）内聚力和黏结力被添加到法向和切向力中[11]。然而，以上3类模型中均未涉及到土壤的塑性行为。Walton等[12]针对塑性材料创建延迟弹性模型（hysteretic spring contact model，HSCM）。当外力未达到预先设定的应力强度时，颗粒间执行线弹性方程；当颗粒接触面的总应力超过设定的应力时，颗粒间执行塑性方程，即颗粒间总应力超过屈服点后模型有塑性变形行为。Ucgul等[13-14]将线弹性内聚力和黏结力整合进HSCM模型中，通过直剪试验得到不同含水率的剪切强度，土壤贯入试验得到HSCM屈服点，仿真参数静摩擦系数和动摩擦系数通过反复调整匹配土壤试验结果，仿真结果显示改进的HSCM能准确预测不同含水率、作业深度、垂直压力、牵引速度深松犁的水平和垂直阻力，为基于DEM优化农具提供新的思路。

基于以上研究，为了解决利用DEM模拟土壤作业过程在预测农具作业阻力和土壤动态运动时存在失真等问题，考虑颗粒间水对土颗粒流动特性的影响，将线性内聚力模型（liner cohesion model，LCM）整合到HSCM模型中建立6种不同含水率西北旱区农田土壤模型，并对该模型所需参数进行标定，以期为西北旱区农田土壤离散元仿真参数标定提供参考。

1 离散元土壤模型建立

1.1 接触模型整合

试验土壤为沙壤土，既有散粒体物料特性又有一定的压缩性。采用的土壤接触模型为HSCM，并在其法向增加LCM，如图1a所示。土壤的弹塑性如图1b所示。

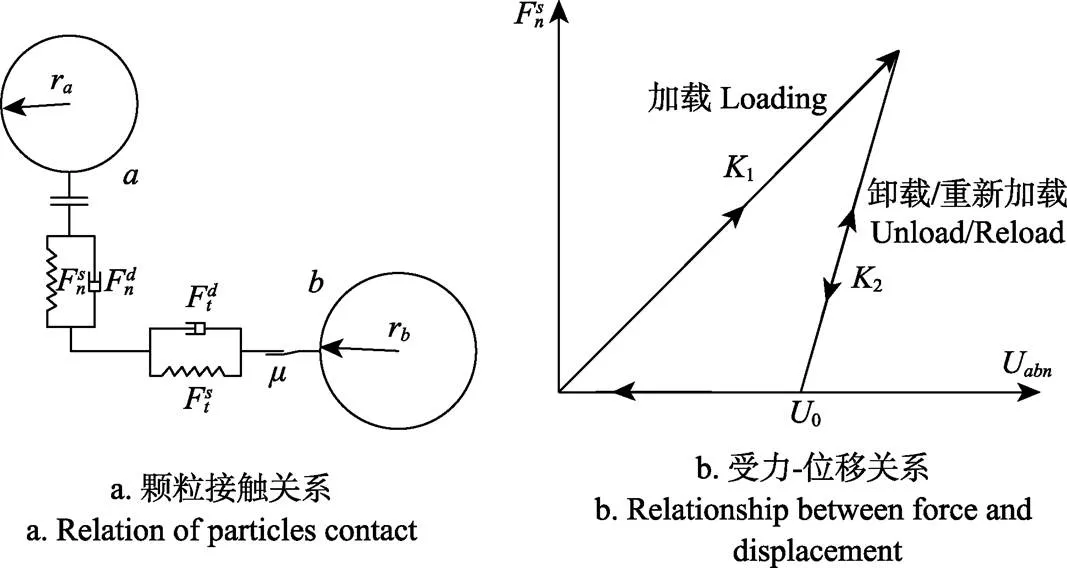
注：ra, rb分别为颗粒a和b的半径，m；,分别为法向接触力和阻尼力，N；,分别为切向接触力和阻尼力，N；μ为摩擦系数；Uabn为颗粒间的法向重叠量，m；U0为颗粒间的残余重叠量，m；K1, K2分别为加载和卸载刚度，N×m-1。下同。

在HSCM中法向接触力定义为

式中r等效半径，m；Y和Y为分别为颗粒和的屈服强度，Pa；屈服强度的默认值（Pa）可以用杨氏模量和颗粒半径预估。

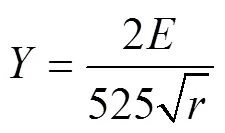
式中若＜100 Pa，可用0.003代替[12]。

卸载刚度为

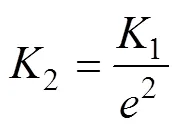
式中为颗粒间的恢复系数。

每个时间步残余重叠量由式（5）更新。

切向接触力定义为

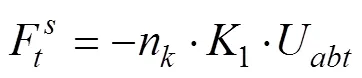
法向和切向阻尼力分别为

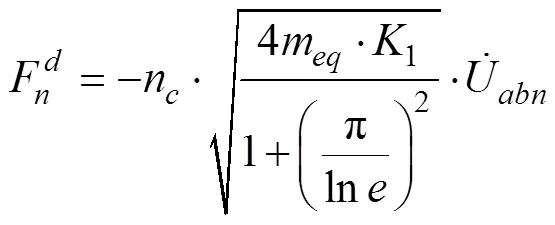
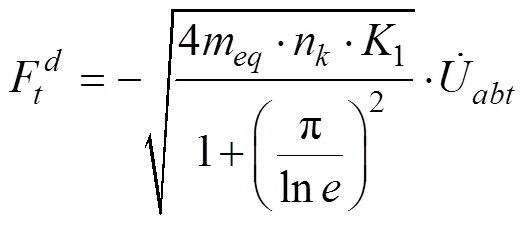
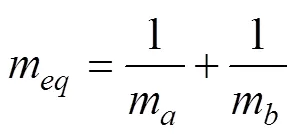
将内聚力施加到法向力中。

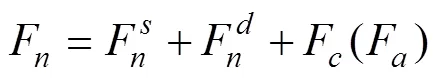
式中F和F分别为颗粒与颗粒的内聚力、颗粒与接触物间的黏结力，N。

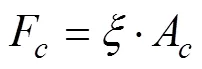
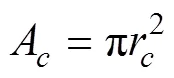
式中r颗粒接触半径，m。

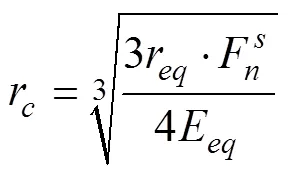
式中E为等效杨氏模量，Pa。

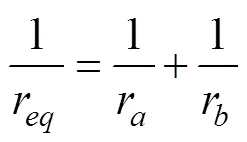
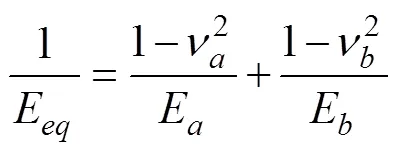
式中E和E分别为颗粒和的杨氏模量，v,v分别为颗粒和的泊松比。

1.2 仿真模型参数确定

根据HSCM及LCM确定土壤基本物理参数、接触力学参数和接触模型参数。基本物理参数包括颗粒粒径分布、土粒密度、剪切模量、泊松比、容重。由于水的作用，土壤颗粒群内形成的液桥使土壤颗粒之间产生内聚力，本文通过土壤剪切试验获取不同含水率土壤的抗剪强度和内摩擦角，LCM模型参数能量密度分别等于6种不同含水率条件下的土壤内聚强度，HSCM模型参数屈服强度通过土壤贯入试验获得，颗粒间的阻尼系数和刚度系数采用EDEM软件默认值，分别为0.05、0.95[15-17]。接触力学参数包括恢复系数、静摩擦系数和动摩擦系数。

1.2.1 土壤基本物理参数

通过标准土壤筛筛分试验可知80%的颗粒尺寸介于0.25和5 mm之间。由于在大多数土壤中，矿物质颗粒约占土壤固相物质质量的95%以上，离散元软件模拟土壤颗粒需要用到土粒密度，取土粒密度值为2 600 kg/m3[18-19]。土壤弹性模量试验测量困难，通过查阅文献[20-21]来获得土壤的弹性模量。

土壤剪切模量表征着土壤抵抗切应变的能力[21]，可由弹性模量和泊松比近似确定，如式（15）所示。

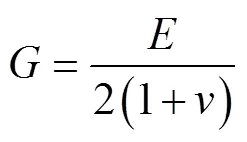
式中为弹性模量，Pa；为泊松比。

土壤的泊松比是指土壤在无侧限条件受压时，侧膨胀应变与竖向压缩应变的比值，通常按公式估算泊松比的值，根据材料力学中广义胡克定律可推导求得土壤侧压力系数与泊松比的相互关系[22]，同时查阅相关文献和资料，泊松比取值范围为0.3～0.42[23-25]。泊松比通过式（16）计算。

式中0为侧压力系数。

土壤侧压力系数是指土壤在侧限条件下受压时，侧向压力与竖向压力的比值，根据经验公式由土壤的内摩擦角由式（17）近似求得[23]。

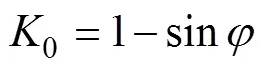
式中为内摩擦角，（°）。

为制备不同含水率土壤进行堆积角试验和直接剪切试验，通过式（18）制备。

式中1为制备试样所需要的加水量，kg；0为基土质量，kg；0为基土含水率，%；1为制样要求的含水率，%。

将土壤存放于塑料袋中24 h，使其水分均匀，用环刀切取土壤并称质量，土壤容重可由式1=/计算得到，通过式（19）可得不同含水率土壤的孔隙率。

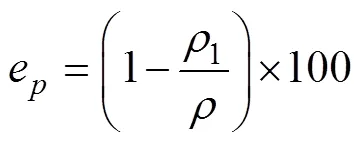
式中e为土壤孔隙率，%；1为土壤容重，kg/m3；为土颗粒密度，kg/m3。

内摩擦角、抗剪强度等力学参数对仿真结果准确性起着非常重要的作用。本文采用快剪试验测定6种含水率在3种垂直压力（70.22、151、256 kPa）下的的土壤的抗剪强度，根据土壤的剪切强度与垂直压力关系获取土壤的抗剪强度、内摩擦角等力学参数[26-29]。试验仪器：南京土壤仪器厂/ZJ型应变控制直剪仪，1000N-S型拉压力传感器，精度0.001 g的电子天平。将剪切速率控制在0.8 mm/min左右，3～5 min内剪破。通过计算获得不同含水率土壤的体积密度、孔隙率、泊松比和剪切模量，如表1所示。

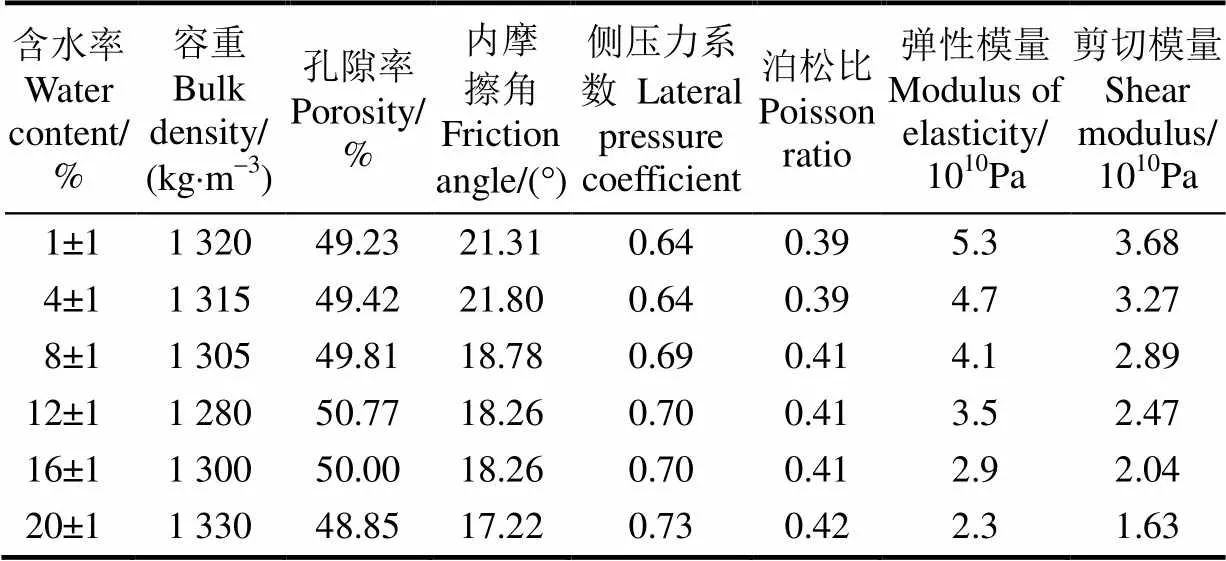
表1 6种不同含水率土壤试验数据

1.2.2 接触力学参数

仿真颗粒的大小受限于计算能力，仿真时间是随着生成的颗粒数量的增加而变长，建立与实际土壤颗粒大小的颗粒模型较难。试验发现80%的颗粒尺寸介于0.25和5 mm之间。通过查阅资料可知，肥沃土壤的结构形态由土壤黏结成粒状和小团块状，大体呈球形。基于以上原因，同时为大幅缩短仿真时间，本文采用半径为5 mm球体作为土壤基体，选择球径倍率分布为0.95～1.05。为使仿真结果接近试验结果，需对半径5 mm仿真颗粒的接触参数进行校核。

在进行参数校核之前需测定6种含水率土壤的堆积角。采用无底的有机玻璃圆柱筒（内径54 mm´高度270 mm）装填土壤至一定高度后，缓慢抬起圆柱筒，待土壤坡面稳定后，垂直拍照，导入CAD软件中标注土壤堆积角。不同含水率土壤堆积角如图2所示。由图2可知，随土壤含水率由1%±1%增大至20%±1%，土壤堆积角由34.14°降至21.2°。

图2 试验中6种含水率土壤堆积角

通过仿真采用整合LCM和HSCM模型的土壤颗粒的堆积试验，对堆积后形成的倾角与测得的内摩擦角进行对比。颗粒半径大小为5 mm，颗粒生成质量通过前文的土壤容重进行计算，时间步长为1×10-5s，在一个圆柱体内生成颗粒，完毕后撤掉圆柱体，让颗粒自然堆积。如图3为不同静摩擦系数、动摩擦系数和抗剪强度条件下的仿真土壤堆积角。由图3可知，随静摩擦系数由0.23增加至0.53，动摩擦系数和抗剪强度在相等条件下仿真土壤堆积角增大；随动摩擦系数由0.16增加至0.30，静摩擦系数和抗剪强度在相等条件下仿真土壤堆积角增大；随抗剪强度由3.47 kPa增加至18.58 kPa，静摩擦系数和动摩擦系数在相等条件下仿真土壤堆积角增大。

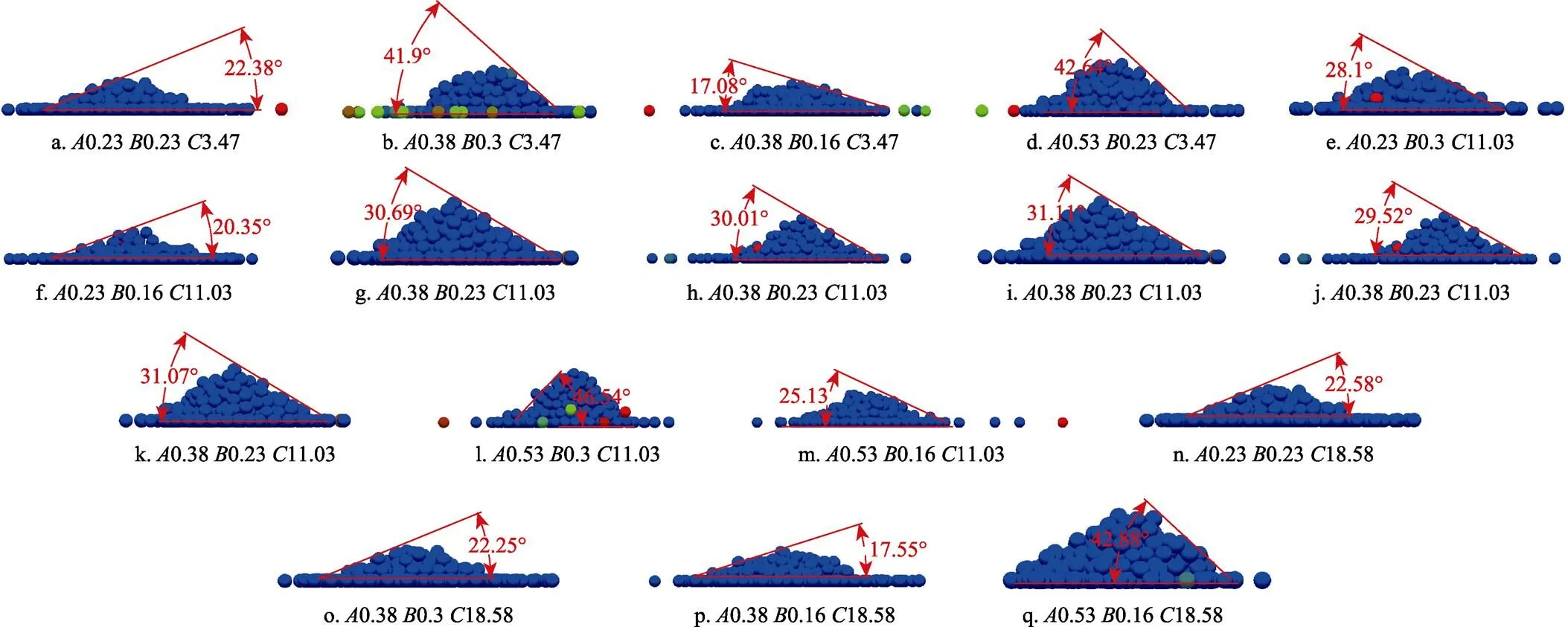
注：A0.23 B0.23 C3.47代表静摩擦系数0.23-动摩擦系数0.23-抗剪强度3.47 kPa。

为后续研究方便，依据中心试验设计方法，建立土壤仿真模型接触参数预测模型。采用Box-Behnken设计模型能用较少的试验次数进行全面的分析研究。以静摩擦系数、动摩擦系数和抗剪强度为仿真试验因素，仿真土壤堆积角为响应值，对各试验因素水平进行编码，依响应面法试验安排共实施17组仿真试验见表2。

表2 仿真试验方案及结果

应用Design-Expert.8.06软件对仿真试验结果进行二次回归分析，结果表明，静摩擦系数、动摩擦系数、动摩擦系数和抗剪强度的交互项、动摩擦系数的二次项对仿真堆积角的影响极显著（＜0.05）；静摩擦系数和动摩擦系数的交互项、静摩擦系数的二次项对仿真堆积角的影响显著（0. 05＜＜0.1）；抗剪强度、静摩擦系数和抗剪强度的交互项和抗剪强度的二次项对仿真堆积角影响不显著（＞0.1）。剔除不显著项，最终获得仿真堆积角回归方程为

=-30.84-146.67+478.02+324.29-9.62+164.612-849.742（20）

式中为静摩擦系数的水平值；为动摩擦系数的水平值；为抗剪强度的水平值；为堆积角，(°)。

以实际土壤堆积角（图2）为优化目标，将快剪试验得到的抗剪强度作为已知值，根据回归模型（1）预测相应的静摩擦系数和动摩擦系数，结果如表3所示。

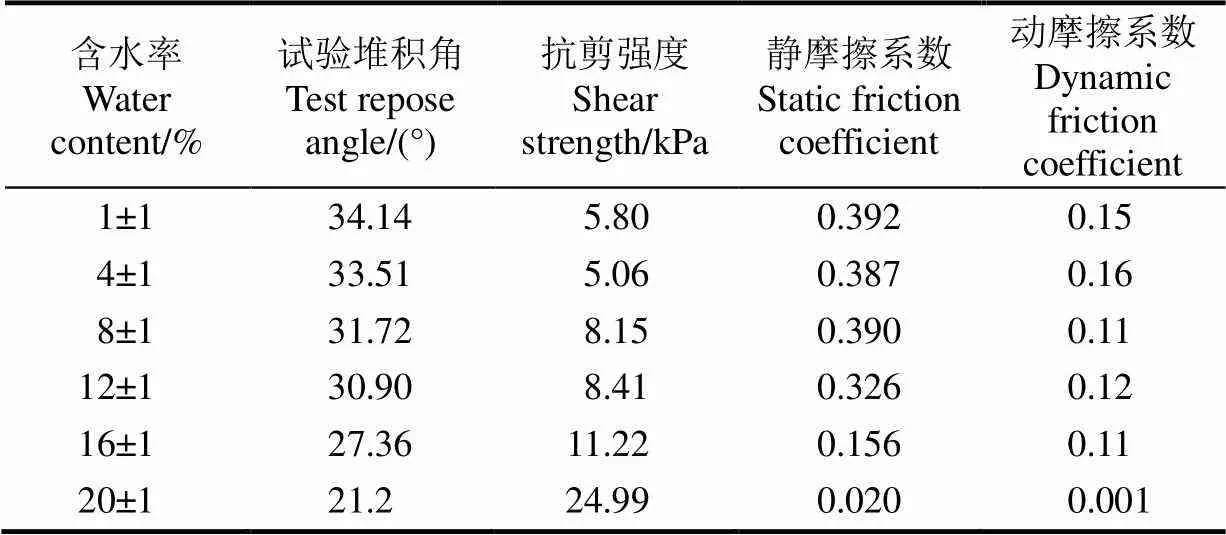
表3 预测的土壤静摩擦系数和动摩擦系数

1.2.3 参数校核

通过直剪仿真试验对预测的土壤的静摩擦系数和动摩擦系数进行校核。直剪仿真试验如图4所示。根据直剪试验原理，建立剪切仿真试验装置，分上盒、下盒和压力板，上盒、下盒外径为62 mm，高10 mm，下盒上口开、下口闭，上盒上下口均开。通过对压力板添加较小垂直向下速度来添加土壤模型垂直载荷。然后给下剪切盒一定的水平速度其大小为1 mm/s，下盒水平位移量达到6 mm时停止仿真，在此期间取峰值作为剪切强度，无峰值取4 mm处值。

图4 直剪仿真试验

将6种含水率条件下土壤快速直剪仿真与试验得到的内摩擦角和抗剪强度进行对比。由表4可知，当含水率为1%～20%时，仿真与试验间的抗剪强度相对误差为1.18%～9.31%，仿真与试验间的内摩擦角相对误差为0.55%～4.07%，可以认为土壤快速直剪仿真结果与试验结果近似一致。

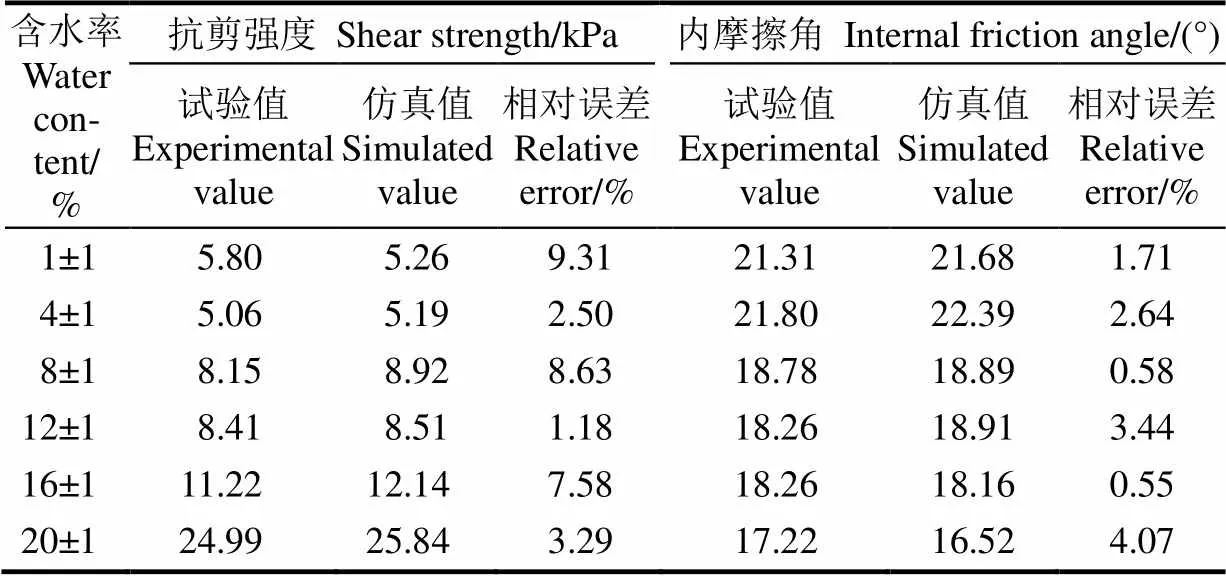
表4 6种含水率的仿真土壤抗剪强度与摩擦角

为了获取含水率为1%的土壤屈服强度，通过自制的土壤贯入试验装置获取壤贯入试验压力-沉陷曲线，土壤贯入工具如图5a所示。试验中土壤贯入试验工具以 1 mm/s速度贯入土壤。得到的土壤贯入试验压力-沉陷曲线如图5b所示。如图所示，在轴方向0～12 mm区间，由于传感器精度问题，未有应力值；随着工具继续深入，当位移量处于轴方向12～26 mm区间时应力与位移量基本趋于直线关系；当位移量处于轴方向26～40 mm区间时，应力与位移量呈下弯走势；当位移量继续增加，土壤发生失效，应力极速下降，此时的土壤受到的应力值为0.23 MPa，最后趋于平缓。因此，HSCM接触模型的屈服强度参数为0.23 MPa。

最终获得的土壤离散元法仿真模型所需参数中，土壤含水率、泊松比、剪切模量见表1，土壤静摩擦和动摩擦系数见表3，其他参数值见表5。

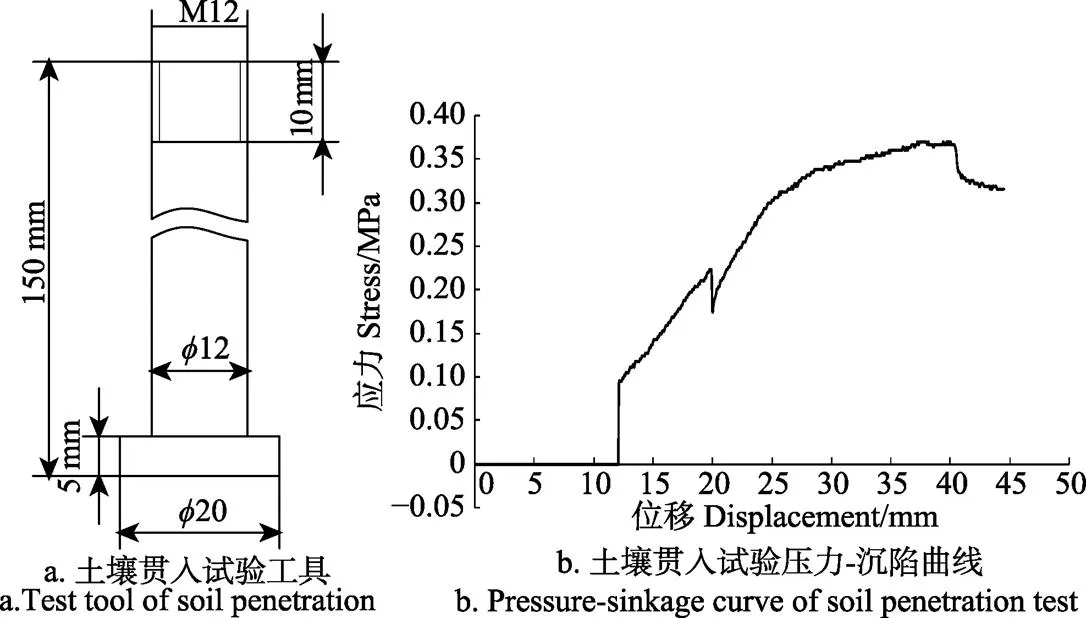
图5 土壤贯入试验工具及压力-沉陷曲线

表5 离散元法仿真的参数

2 验证试验

2.1 鸭嘴插入土壤模型仿真

直插穴播工作过程中鸭嘴与土壤的接触、垂直受力是鸭嘴设计重点。本文采用的直插鸭嘴验证模型为韩国产提携直插式玉米播种器，如图6a所示。鸭嘴模型通过Solidworks软件建模，鸭嘴模型具体尺寸如图6b所示。将鸭嘴模型导入EDEM 中并设置材料参数与运动属性参数，使用土壤含水率为1%对应土壤参数建立土壤模型，土壤颗粒半径大小为5 mm，球径倍率分布为0.95～1.05，仿真土槽模型外径100 mm、高100 mm，未仿真之前调整鸭嘴尖距土槽上面2 mm，仿真时鸭嘴垂直插入土槽速率为1 mm/s，时间步4.17´10-6s，仿真总时间为50 s，使用压板压实土壤模型使其孔隙率为49.23%，压板速率为1 mm/s。试验前，调整鸭嘴处于圆形土槽中间位置，并使鸭嘴尖离2 mm，设置鸭嘴垂直插入土壤速率为 1 mm/s，当鸭嘴尖插入土壤5 s时停止运动，将传感器鸭嘴入土阻力导入电脑进行处理。试验装置为HDV-1K电动双柱拉压力测试台。其他条件与试验一致。仿真时测量鸭嘴受到土壤模型的垂直阻力，当鸭嘴进入土壤模型50 mm处停止鸭嘴运动。建立的鸭嘴-土壤模型如图6c所示。

2.2 结果与分析

通过比较仿真与试验中鸭嘴插入土壤过程入土阻力来验证所标定土壤参数的可靠性。由于优化鸭嘴结构尺寸一般参考鸭嘴入土阻力的最大值，通过比较不同结构尺寸鸭嘴的入土阻力来确定最优结构，因此，本文重点比较在同等条件下仿真和试验垂直入土阻力的误差，兼参考曲线走势进行仿真模型和参数验证。鸭嘴插入土壤试验装置如图7a所示。

1. 固定鸭嘴 2. 活动鸭嘴 3. 固定座 4. 排种轮 5. 种管 6. 把手 7. 支撑座 8. 弯顶杆 9. 弹簧 10. 导杆

注：Re为相对误差。

对仿真和试验鸭嘴插入阻力数据进行分析（图7b）可知，仿真与试验曲线在入土距离处于0～50 mm期间时，仿真和试验阻力走势相差不大，但仿真入土阻力曲线波动较大，分析原因可知，由于采用半径为5 mm的土颗粒，与实际土颗粒相差较大，虽然能大幅度减少仿真时间，但不可避免会产生入土阻力波动较大的问题。玉米直插穴播最深处50 mm处的仿真和试验入土阻力相对误差为0.928%，此时的仿真入土阻力最大，可利用最大阻力值分析直插鸭嘴结构对其强度的影响。

3 结 论

1）提出将HSCM和LCM整合于一体模拟西北农田土壤，利用Box-Behnken试验法建立以静摩擦系数、动摩擦系数和抗剪强度为因素、以土壤仿真堆积角为指标的数学回归模型，并借助土壤直接剪切仿真试验对静摩擦和动摩擦系数参数进行校核，校核结果发现：6种不同含水率土壤直接剪切仿真和试验中，当含水率为1%～20%时，仿真与试验间的抗剪强度相对误差为1.18%～9.31%，仿真与试验间的内摩擦角相对误差为0.55%～4.07%，表明HSCM和 LCM组合模型是可行的。

2）通过鸭嘴插穴土壤仿真与实际对比检验2种土壤接触模型的适应性以及预测的静摩擦系数和动摩擦系数的可靠性，结果表明：仿真与试验曲线在入土距离处于0～50 mm期间时，但仿真入土阻力曲线波动较大，仿真和试验阻力走势基本一致，玉米直插穴播最深处50 mm处的仿真和试验入土阻力相对误差为0.928%，此时的仿真入土阻力最大，可利用最大阻力值分析直插鸭嘴结构对其强度的影响。

[1] Zadeh S R A. Modelling of Energy Requirements by a Narrow Tillage Tool[D]. Saskatoon: University of Saskatchewan, 2006.

[2] 赵成刚. 土力学的现状及其数值分析方法中某些问题的讨论[J]. 岩土力学，2006，27(8)：1361－1364.Zhao Chenggang. Discussion on state-of-art of soil mechanics and some problems with applications of numerical method to geotechnical engineering[J]. Rock and Soil Mechanics, 2006, 27(8): 1361－1364. (in Chinese with English abstract)

[3] Godwin R J, O’Dogherty M J, Saunders C, et al. A force prediction model for mould board ploughs incorporating the effects of soil characteristic properties, plough geometric factors and ploughing speed[J]. Biosystems Engineering, 2007, 97(1): 117－129.

[4] Asaf Z, Rubinstein D, Shmulevich I. Evaluation of link-track performances using DEM[J]. Journal of Terramechanics, 2006, 43(2): 141－161.

[5] Karmakar S, Ashrafizadeh S R, Kushwaha R L. Experimental validation of computational fluid dynamics modeling for narrow tillage tool draft[J]. Journal of Terramechanics, 2009, 46(6): 277－283.

[6] Tsuji T, Nakagawa, Matsumoto N, et al. 3D DEM simulation of cohesive soil pushing behavior by bulldozer blade[J]. Journal of Terramechanics, 2011, 49(1): 37－47.

[7] 张锐，李建桥，李因武，等. 部件复杂表面影响土壤扰动行为的离散元宏细观分析[J]. 吉林大学学报：工学版，2009，39(5)：1218－1223. Zhang Rui, Li Jianqiao, Li Yinwu, et al. DEM macroscopic and mesoscopic analysis in disturbed behavior of soil acted by part with complex surface[J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(5): 1218－1223. (in Chinese with English abstract)

[8] 石林榕，吴建民，赵武云，等. 基于离散单元法农田土壤单轴压缩模型的建立及参数校核[J]. 中国农业大学学报，2015，20(4)：174－182. Shi Linrong, Wu Jianmin, Zhao Wuyun, et al. Establishment and parameter verification of farmland soil model in uniaxial compression based on discrete element method[J]. Journal of China Agricultural University, 2015, 20(4): 174－182. (in Chinese with English abstract)

[9] Ucgul M, Fielke J M, Saunders C. Three-dimensional discrete element modelling of tillage: Determination of a suitable contact model and parameters for a cohesionless soil[J]. Biosyst Eng, 2014, 121(2): 105－117.

[10] Ucgul M, Fielke J M, Saunders C. 3D DEM tillage simulation: validation for a sweep tool for a cohesionless soil[J]. Soil Till Res, 2014, 144(4): 220－227.

[11] Momozu M, Oida A, Yamazaki M, et al. Simulation of a soil loosening process by means of the modified distinct element method[J]. Journal of Terramechanics, 2002, 39(4): 207－220.

[12] Walton O R, Braun R L. Stress calculations for assemblies of inelastic spheres in uniform shear[J]. Acta Mechanica, 1986, 63(1/2/3/4): 73－86.

[13] Ucgul M, Fielke J M, Saunders C. Three-dimensional discrete element modelling (DEM) of tillage: accounting for soil cohesion and adhesion. Biosyst Eng, 2015, 129(5): 298－306.

[14] Ucgul M, Fielke J M, Saunders C. Three-dimensional discrete element modelling of tillage: determination of a suitable contact model and parameters for a cohesionless soil[J]. Biosystems Engineering, 2014, 121(2): 105－117.

[15] DEM Solution Ltd. EDEM 2.5 theory reference guide[R/OL]. 2014-12-05[2015-06-07].http://www.docin.com/p- 980174717.html

[16] 胡国明. 颗粒系统的离散元素法分析仿真[M]. 武汉：武汉理工大学出版社，2010.

[17] 王国强. 离散单元法及其在EDEM上的实践[M]. 西安：西北工业大学出版社，2010.

[18] 邵明安，王全九，黄明斌. 土壤物理学[M]. 北京：高等教育出版社，2006：20－51.

[19] 邓时琴.土壤矿质颗粒及土壤质地[J].土壤，1983(2)：77－80. Deng Shiqin. Soil mineral particles and soil texture[J]. Soil, 1983(2): 77－80. (in Chinese with English abstract)

[20] 董晓丽，李文利. 土力学与基础工程[M]. 北京：清华大学出版社，2009：17－42.

[21] Academia. Some useful numbers for rock sand soils [R/OL].

2014-12-28 [2015-11-17]. http://www.academia.edu/4056287/ Some_Useful_Numbers_for_rocks_and_soils. 2015.

[22] 钱立彬.基于离散元法的开沟器的数字化设计方法研究[D]. 长春：吉林大学，2009：15－36.

Qian Libin. Digital Design Method of Furrow Openers Based On DEM[D]. Changchun: Jilin University, 2009: 15－36.

[23] Cheng Y P, Nakata Y, Bolton M D. Discrete element simulation of crushable soil[J]. Geotechnique, 2003, 53(07): 633－641.

[24] 李艳洁，吴腾，林剑辉，等. 基于离散元法的贯入圆锥对沙土颗粒运动特性分析[J]. 农业工程学报，2012，28(24)：55－61.

Li Yanjie, Wu Teng, Lin Jianhui, et al. Influence of penetrating cone on motion characteristics of sandy soil particle using discrete element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(24): 55－61. (in Chinese with English abstract)

[25] 文建鹏.长沙典型粉质粘土的三轴试验及本构模型研究[D]. 长沙：中南大学，2004. Wen Jianpeng. Triaxial Test and Constitutive Model on the Silty Clay in Changsha Area[D]. Changsha: Central South University, 2004. (in Chinese with English abstract)

[26] 杨菊. 基于扩展有限元法和离散元法的土壤-耕具接触研究[D]. 昆明：昆明理工大学，2014. Yang Ju. Analysis of Soil-Tool Interaction Using Extended Finite Element Method and Discrete Element Method[D]. Kunming: Kunming University of Science and Technology, 2014. (in Chinese with English abstract)

[27] 孙红月. 土力学实验指导[M]. 北京：中国水利水电出版社，2010：50－79.

[28] 董晓丽，李文利. 土力学与基础工程[M]. 北京：清华大学出版社，2009：110－135.

[29] 南京水利科学研究院土工研究所. 土工试验技术手册[M]. 北京：人民交通出版社，2007：33－49.

[30] Das B M. Advanced Soil Mechanics[M]. New York: Taylor & Francis, 1997: 14－20.

石林榕，赵武云，孙 伟. 基于离散元的西北旱区农田土壤颗粒接触模型和参数标定[J]. 农业工程学报，2017，33(21)：181－187. doi：10.11975/j.issn.1002-6819.2017.21.021 http://www.tcsae.org

Shi Linrong, Zhao Wuyun, Sun Wei. Parameter calibration of soil particles contact model of farmland soil in northwest arid region based on discrete element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(21): 181－187. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.21.021 http://www.tcsae.org

Parameter calibration of soil particles contact model of farmland soil in northwest arid region based on discrete element method

Shi Linrong, Zhao Wuyun※, Sun Wei

(,730070,)

In order to solve simulation distortion problems of soil resistance and dynamic movement with discrete element method, the hysteretic spring contact model (HSCM) and the liner cohesion model (LCM) were used to simulate farmland soils in order to investigate their soil plasticity behavior and dynamics, which could be used for predicting the resistance of farm tools. To achieve better simulation results, soil basic physical parameters, contact mechanical parameters and contact model parameters of HSCM and LCM were needed. Soil basic physical parameters included particle size distribution, soil particle density, elasticity modulus, shear modulus, poisson's ratio and bulk density. Among them, the elasticity modulus was obtained by the related literature. Soil contact mechanical parameters included cohesion between soil particles formed due to the action of the water liquid bridge, cohesive strength and internal friction angle obtained from soil shear test with 6 kinds of different soil moisture. Contact model parameters were composed of coefficient of restitution, static friction coefficient and dynamic friction coefficient. The soil particles were 5 mm so that the simulation time could be shortened. Because soil simulation particles were larger than actual ones, additionally in order to achieve better simulation results, a simulation model of soil contact parameter prediction model was established according to central experimental design method (Box-Behnken) used for a comprehensive analysis of fewer trial times. Taking static friction coefficient, dynamic friction coefficient and shear strength as test factors, and soil accumulation angle as response value, 17 sets of simulation tests were carried out according to response surface method test arrangement. The results showed that the influence of static friction coefficient, dynamic friction coefficient and the interaction between dynamic friction coefficient and cohesion strength on repose angle were significant. Interaction between static friction coefficient and dynamic friction coefficient, quadratic term of static friction coefficient had a significant effect on repose angle. Taking repose angle of soil with moisture of 1%, 4%, 8%, 12%, 16% and 20% as the response value, fixing the cohesion strength, we predicted the static friction coefficient and dynamic friction coefficient using the established regression model. Then, the results were validated by soil shear test. The results showed that the relative error of shear strength was 1.18%-9.31%, and the relative error of internal friction angle was 0.55%-4.07%. In order to verify the feasibility of the proposed soil contact model, a test by using duckbill opening hole test device in soil was carried out and the results showed that when the displacement was 0-50 mm the deviation of simulation and test was big. But when the displacemtn was 50 mm, the relative error was 0.928%, which could be used for design of duckbill structure in the future.

soils; discrete element method; friction coefficient; parameters; calibration

10.11975/j.issn.1002-6819.2017.21.021

O347.7;S22

A

1002-6819(2017)-21-0181-07

2017-03-05

2017-10-10

农业部公益性行业科研专项（2015-03105）；甘肃省高等学校科研项目（2016B-039）；甘肃农业大学盛彤笙科技创新基金（GSAU-SLS-1623）

石林榕，助教，主要从事西北旱区农业工程技术与装备研究。Email：getmao@qq.com

※通信作者：赵武云，教授，博士生导师，主要从事农业工程技术与装备研究。Email：zhaowy@gsau.edu.cn

中国农业工程学会高级会员：石林榕（E041200842S）