一种基于多普勒频率的恒模信号直接定位方法
2017-11-20王鼎尹洁昕吴志东刘瑞瑞
王鼎, 尹洁昕,*, 吴志东, 刘瑞瑞
1.解放军信息工程大学 信息系统工程学院, 郑州 450001 2.国家数字交换系统工程技术研究中心, 郑州 450002
一种基于多普勒频率的恒模信号直接定位方法
王鼎1,2, 尹洁昕1,2,*, 吴志东1, 刘瑞瑞1
1.解放军信息工程大学 信息系统工程学院, 郑州 450001 2.国家数字交换系统工程技术研究中心, 郑州 450002
相比于传统的差分多普勒(DD)两步定位方法,以Amar和Weiss提出的基于多普勒频率的单步直接定位方法在低信噪比和小样本条件下具有更高的定位精度。在该类新型定位体制的基础上,提出了一种基于多普勒频率的恒模信号直接定位方法。首先,依据最大似然(ML)准则以及恒模信号的恒包络特征,建立相应的直接定位优化模型。然后,根据目标函数的代数特征将全部未知参量分成两组,并提出一种有效的多参量交替迭代算法,用以获得该优化问题的最优数值解。新算法包含了针对这两组未知参量的Newton型迭代公式,用以避免网格搜索,并能实现多维参数的“解耦合”估计。最后,推导出针对恒模信号的目标位置直接估计方差的克拉美罗界(CRB)。数值实验验证了新方法的优越性。
无源定位; 直接位置确定; 多普勒频率; 恒模信号; 最大似然估计; Newton型迭代; 克拉美罗界
众所周知,无线电信号定位对于无线通信、遥测导航、目标检测、电子对抗等诸多工程物理科学领域具有广泛应用。无线定位的基本过程是从接收信号中提取出与目标位置相关的参数(也称定位观测量),然后再从这些参数中获得关于目标的位置信息。用于目标定位的观测量涉及到空、时、频、能量等多域参数,其中最为典型的观测量包括:到达时间差(Time Difference of Arrival, TDOA)[1]、到达频率差(Frequency Difference of Arrival, FDOA)[2]、到达信号增益比(Gain Ratio of Arrival, GROA)[3]、到达角度(Angle of Arrival, AOA)[4]、到达时间(Time of Arrival, TOA)[5]、到达频率(Frequency of Arrival, FOA)[6]、接收信号强度(Received Signal Strength, RSS)[7]等。根据上述观测量可以建立关于目标位置参数的代数方程,通过优化求解该方程即可确定目标位置信息。
一般而言,不同的定位观测量适用于不同的信号类型和定位场景,例如,宽频带信号适用于TDOA定位,窄频带或者点频信号适用于AOA、FOA以及FDOA定位。需要指出的是,FOA和FDOA参数都是由于信号的多普勒效应所产生的,其主要应用于目标和观测站之间存在径向速度的场景中。事实上,基于多普勒频率的无线定位也是一种十分重要的定位体制,其中最具代表性的方法是差分多普勒(Differential Doppler, DD)定位法[8-9],该方法利用不同观测站接收到同一信号时所产生的多普勒频差来实现定位,这种定位方式也称为两步定位法。所谓两步定位是指先从观测站接收到的信号数据中提取定位参数,然后再基于该参数确定目标的位置信息,这也是目前无线定位系统中采用的主流方法。
尽管两步定位法广泛应用于各类无线定位系统中,但以Weiss和Amar为代表的一些学者却系统总结了该类定位方法存在的若干不足,比如,估计方差难以达到渐近最优、多目标分辨能力较弱以及存在数据关联等问题。与此同时,以他们为代表的诸多学者还提出一类新型无线定位体制[10-26],即目标位置直接确定(Direct Position Determination, DPD)或称直接定位(Direct Localization, DL)技术。该类定位方法的基本思想是从观测站接收到的信号数据中直接获得目标位置信息,而无需估计其他中间参量。通过大量实验可以验证,在低信噪比(SNR)和小样本条件下,DPD方法比传统两步定位方法具有更高的定位精度,并且能够有效避免数据关联问题。值得一提的是,随着通信带宽和计算能力的提升,DPD方法可应用于多种无线定位体制中,而针对多普勒频率定位体制,Weiss和Amar也专门设计了相应的DPD方法[14],相比于前面提到的DD定位法,该DPD方法的优势是显著的。另一方面,DPD方法还存在一个潜在的优势就是其能直接融合信号时域波形信息,例如,文献[10-12,14,23]提出了信号波形已知条件下的DPD方法,而文献[15-17,26]则依次提出了针对多输入多输出(MIMO)雷达信号、OFDM信号、循环平稳信号以及恒模信号的DPD方法。大量实验结果表明,通过利用信号时域波形信息可以显著提升目标定位精度。
在通信信号处理中,一类恒模信号(即相位调制信号)得到广泛应用[27-29],例如,模拟域的调频(FM)和调相(PM)信号等,数字域的FSK,PSK,4-QAM 信号等。该类信号的显著特点是其复包络具有恒模特性,若能够将这一特征利用到目标定位中,则将有助于提升目标位置估计精度。例如,文献[26]提出的DPD方法正是融入了信号的恒模特性,但其中采用单个天线阵列接收信号,所以它是基于信号方位信息所提出的定位方法,没有考虑信号的多普勒效应,并不属于多普勒定位体制。本文则是在文献[14]提出的基于多普勒频率的DPD方法的基础上,提出了一种基于多普勒频率的恒模信号DPD方法。文中首先依据最大似然(Maximum Likelihood, ML)准则以及恒模信号的恒包络特征,建立相应的DPD优化模型。然后,根据目标函数的代数特征将全部未知参量分为两组,并随之提出一种有效的多参量交替迭代算法,用以获得该优化问题的最优数值解。在新提出的交替迭代算法中,根据两组未知参量的数学模型分别设计出相应的Newton型迭代公式,用以避免网格搜索,并能实现多维参数的“解耦合”估计,以使得新算法具有快速收敛性和稳健性。最后,文中还推导了目标位置直接估计方差的克拉美罗界(Cramér-Rao Bound, CRB),从而为DPD方法的参数估计精度提供定量的理论参考。数值实验表明,新方法的统计性能可以渐近逼近相应的CRB,通过利用恒模信号的恒包络特性可以提高目标定位精度(相比没有信号时域波形信息的条件下)。
1 信号模型与预备结论
1.1 信号模型
假设有一个待定位的静止辐射源,其位置向量为q(维数为D),该目标辐射恒包络信号(即相位调制信号),并且该信号能够同时被N个运动观测站截获。每个观测站将在K个时隙段内对目标辐射信号进行采样,相邻两个采集时隙段的时间间隔为T。为了能够对该目标进行直接定位,这里需要做出以下两点假设[14]:

2) 目标辐射窄带信号,并且信号带宽B小于信号到达不同观测站的时延最大值τmax的倒数(即B<1/τmax),于是信号到达不同观测站的复包络是一致的。
基于上述讨论和假设,第n个观测站在第k个时隙段内截获到的无线电信号模型可以表示为

xn,k(t)+εn,k(t)
(1)
式中:sk(t)为信号在第k个时隙段内的复包络,文中假设该复包络具有恒模特性,不失一般性,这里将其表示为sk(t)=exp(jφk(t)),φk(t)为其相位调制分量;εn,k(t)为零均值复圆高斯白噪声,其方差为σ2;βn,k为信号在第k个时隙段到达第n个观测站的复传播系数;fn,k为第n个观测站在第k个时隙段截获到的信号频率,该频率可以表示为[14]
fn,k=(fc+Δfk)(1+γn,k(q))
(2)
式中:fc为信号载波频率的标称值(该值可认为是已知量);Δfk为由于目标辐射信号的不稳定而导致的频率漂移;γn,k(q)为由目标与观测站之间的相对运动而产生(即多普勒效应),其代数表达式为

(3)
式中:v为无线电信号的传播速度。需要指出的是,通常有γn,k(q)≪1和Δfk≪fc,于是fn,k可以近似表示为
fn,k≈fc+Δfk+fcγn,k(q)
(4)
由于fc是已知量,因此通过数字下变频处理后所得到的信号频率为
(5)
假设观测站的信号采样时间间隔为Ts,并且在每个时隙段共采集到了L个信号样本点,若将这L个信号采样值合并成向量形式就可以得到如下观测模型:
βn,kAn,k(q)B(Δfk)sk+εn,k=
βn,kAn,k(q)Skb(Δfk)+εn,k
(6)
式中:
(7)
为了便于后续的理论分析,这里定义如下参数向量
(8)

1.2 预备结论
在给出新的DPD方法之前,这里先给出文中证明的一个预备结论,并以命题形式给出。

(9)
式中:
(10)
命题1的证明见附录A,其中的结论对于文中DPD方法的推导至关重要。
2 恒模信号直接定位方法
2.1 直接定位方法的基本思想
上述直接定位问题本质上还是属于信号参数估计问题,为了获得渐近最优的估计精度,通常利用最大似然准则进行求解。在高斯噪声条件下,最大似然准则等价于如下最小二乘估计准则:

(11)
显然,式(11)是一个多维非线性优化问题,其闭式解无法获得,仅能利用迭代法求其数值解。由于式(11)中共包含4种不同的未知参量(种类较多),因此可以选择交替迭代算法进行数值寻优。该算法的基本思想是,在每次迭代中仅针对部分未知参量进行优化计算,并保持其余未知参量固定不变,依次进行直至收敛为止。
根据式(11)中目标函数的代数特点,本文提出的交替迭代算法将未知参量分成两组:第1组包含Δf和q;第2组包含β和φ。每一轮迭代中将包含两个运算单元:第1个是在β和φ固定不变的情况下对Δf和q进行优化计算;第2个则是在Δf和q固定不变的情况下对β和φ进行优化计算。2.2节将推导其具体计算过程。
2.2 交替迭代算法的数学推导
2.2.1 参量Δf和q的优化


(12)
式中:

(13)

显然,式(12)的闭式解无法获得,只能利用数值迭代的方式进行求解。注意到Δfk是一个仅与k有关系的标量,而且关于它的优化求解可以通过FFT算法来实现[14],因此不妨将其作为“隐变量”来处理(即并不显式参与优化),此时可以将式(12)看成是仅关于位置向量q的优化问题,即有

(14)
式中:
wk(Δfk,q)=(ck(q))HEk(Δfk)ck(q)
(15)
其中:
(16)
式(16)中的第2个等式利用了矩阵恒等式vec(XYZ)=(ZT⊗X)·vec(Y),而J1则是满足等式vec((Ck(q))T)=J1·vec(Ck(q))的置换矩阵。
由于“隐”变量Δfk的存在,式(14)中目标函数w(q)并不是关于位置向量q的显式表达式,此时求解式(14)最易操作的方法就是网格搜索[14],但这会导致较大的运算量,尤其是对定位精度要求较高的条件下(因为搜索步长较小,网格点数较多)。为此,这里将给出一种求解式(14)的Newton迭代公式,它可以快速收敛至其最优解,但瓶颈在于目标函数w(q)的梯度向量gr(q)和Hessian矩阵Gr(q)的表达式无法直接获得,这就需要利用命题1中的结论。基于该命题可以推得gr(q)和Gr(q)的表达式分别为
(17)
式中:
(18)

(19)

总结上述讨论可以得到求解式(14)的Newton迭代公式为
(20)

2.2.2 参量β和φ的优化


(21)
从式(21)中不难看出,不同时隙段内的未知参量可以分离并行估计,于是可以将式(21)拆分成如下K个相互独立的子问题

(22)

(23)
式中:(·)†为矩阵或向量的Moore-Penrose广义逆。将式(23)代入式(22)中可以得到仅关于φk的优化问题为
(24)
式中:
(25)

由于式(24)中的目标函数含有正交投影矩阵,此时利用Gaussian-Newton迭代公式可以快速收敛至其最优解[30-31],相应的迭代公式为
(26)
式中:m为迭代数;λ2(0<λ2<1)为步长因子,而向量gt(φk)和矩阵Gt(φk)的表达式分别为
(27)
式中:vecd[·]为提取矩阵对角元素构成的列向量;⊙表示矩阵Schur积(即点乘),而en,k(φk)的表达式为
(28)
2.3 交替迭代算法的总结与讨论
基于上述讨论,下面可以总结出用于DPD的交替迭代算法的计算步骤。

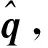


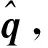
关于上述DPD方法有下述几点说明:
注释2 未知参量q的迭代初值可以通过文献[8-9]中提出的DD定位方法获得(即两步定位方法)。
注释3 步骤2中的一维优化计算可以利用FFT算法来获得(见文献[14]中的附录I),从而有效降低运算量。
注释4 步骤3中φk的迭代初值可事先计算sk的估计值,然后再利用其相位获得,为此可以将βn,k设为1,然后基于式(11)可得sk的近似估计值为
(29)
数值实验表明,由注释2和注释4给出的迭代初始值能够保证算法收敛至较好的解,并且通常在15次迭代以内即可达到收敛。
3 参数估计方差的克拉美罗界
本节将推导未知参数估计方差的克拉美罗界,重点推导目标位置估计方差的克拉美罗界。首先定义如下包含全部未知参数的向量
η=[σ2μT]T=
[σ2qTφTΔfT(Re{β})T(Im{β})T]T
(30)
式中:
μ=[qTφTΔfT(Re{β})T(Im{β})T]T
(31)
接着再定义如下包含全部接收数据的向量
(32)

(βN,KAN,K(q)B(ΔfK)sK)HH
(33)
基于文献[33]中的结论可知,关于参数向量μ的克拉美罗界矩阵可以表示为
(34)
式中:
(35)
利用式(33)可以进一步推得式(35)中各个子矩阵的表达式为
(36)
式中:
(37)
在实际应用中主要关注目标位置向量q的估计方差的克拉美罗CRB(q),但从式(34)中无法直接得到CRB(q)的闭式表达式,这是因为CRB(μ)并不具备块状结构。为了获得CRB(q)的闭式表达式,可以利用文献[34]中的思想,重新定义一个新的参数向量,而关于该新参数向量的克拉美罗界矩阵具有块状结构。新参数向量定义为
(Im{β}+Im{U1}q+Im{U2}φ+Im{U3}Δf)T]T
(38)
式中:
(39)
对比式(31)和式(38)可知
(40)
式中:
(41)
(42)
式中:
(43)
另一方面,根据式(35)、式(39)和式(43)可得
(44)

(45)
式中:
(46)
(47)
(48)
利用分块矩阵求逆公式可以推得CRB(q)的表达式为
(49)
式(49)给出了基于多普勒频率的恒模信号直接定位方差的CRB,第4节的数值实验将表明,文中提出的交替迭代算法的性能可以渐近逼近此CRB,这是由于该DPD方法是基于ML准则推导的,这一准则通常可以提供渐近最优的统计性能。
4 数值实验
4.1 与克拉美罗界进行比较
本节将新提出的DPD方法的性能与式(49)给出的CRB进行比较,以说明该方法在统计性能上的渐近最优性。

首先假设目标辐射窄带调频信号,目标位置设为3种情况,分别为(6,6) km,(8,8) km 和(10,10) km,现有3个运动观测站可以截获其信号,并且每隔10 s就对该信号进行一个时隙段的采样(共有10个时隙段),观测站的运动速度为200 m/s,其运动轨迹与目标位置关系如图1所示。需要指出的是,将目标的位置分组设为3种情况是为了说明目标与观测站之间的距离对于定位精度的影响,从图1中不难看出,第3种情况的目标距离观测站最远,而第1种情况的目标最接近观测站。另一方面,信号的载波频率扰动量在[-100 100] Hz内服从均匀分布,信道传播系数的幅度均设为1,其相位在[-π π]内服从均匀分布。首先将每个时隙段内的样本点数设为50,信号载波频率设为0.2 GHz,图2(a)给出了目标位置估计均方根误差随着信噪比的变化曲线;接着将信噪比设为5 dB,信号载波频率设为0.2 GHz,图2(b)给出了目标位置估计均方根误差随着每个时隙段内样本点数的变化曲线;最后将信噪比设为5 dB,每个时隙段内的样本点数设为50,图2(c)给出了目标位置估计均方根误差随着信号载波频率的变化曲线。
图1 运动观测站与目标位置之间的几何关系(包含3个观测站)Fig.1 Geometry relationship between moving observers and emitter (three observers)

图2 目标位置估计均方根误差的变化曲线(3个观测站) Fig.2 RMSE of source position estimation(three observers)
接着假设有4个运动观测站可以截获其信号,并且每隔5 s对该信号进行一个时隙段的采样(共有10个时隙段),观测站的运动速度为100 m/s,目标的位置仍然设为3种情况,分别为(8,8) km,(10,10) km和(12,12) km,其与运动观测站的位置关系如图3所示。需要指出的是,这里将目标的位置分组设为3种情况也是为了说明目标与观测站之间的距离对于定位精度的影响,从图3中不难看出,第3种情况的目标距离观测站最远,而第1种情况的目标最接近观测站。首先将每个时隙段内的样本点数设为50,信号载波频率设为0.2 GHz,图4(a)给出了目标位置估计均方根误差随着信噪比的变化曲线;接着将信噪比设为5 dB,信号载波频率设为0.2 GHz,图4(b)给出了目标位置估计均方根误差随着每个时隙段内样本点数的变化曲线;最后将信噪比设为5 dB,每个时隙段内的样本点数设为50,图4(c)给出了目标位置估计均方根误差随着信号载波频率的变化曲线。
从图2和图4中可以看出:① 本文提出的DPD方法的定位精度随着信噪比、样本点数以及信号载波频率的增加而提高;② 针对近距离目标的定位精度要高于针对远距离目标的定位精度,也就是说针对第3种情况的目标精度最低,而针对第1种情况的目标精度最高;③ 新方法的性能曲线渐近逼近式(49)给出的CRB曲线,从而说明了新方法的渐近最优性。

图3 运动观测站与目标位置之间的几何关系(4个观测站) Fig.3 Geometry relationship between movingobservers and emitter (four observers)


图4 目标位置估计均方根误差变化曲线(4个观测站)Fig.4 RMSE of source position estimation(four observers)
4.2 与其他定位方法的性能进行比较
本节将文中新提出的DPD方法的性能与文献[14]中的DPD方法以及传统DD方法[8-9]的性能进行比较,以进一步说明新方法的优势。值得一提的是,这几种方法的性能在高信噪比条件下是渐近一致的,但是在低信噪比条件下的性能差异较大,因此本节的数值实验结果均是在低信噪比条件下给出的。另一方面,文献[14]中提出了两种DPD方法,一种用于信号波形未知的场景,另一种则用于信号波形精确已知的情形,下面称前者为“方法1”,称后者为“方法2”。
定位场景和实验参数基本同图1,首先将每个时隙段内的样本点数设为100,信号载波频率设为0.2 GHz,目标位置设为(7,7) km,图5(a)给出了4种定位方法的目标位置估计均方根误差随着信噪比的变化曲线;接着将信噪比设为-7 dB,信号载波频率设为0.2 GHz,目标位置设为(7,7) km,图5(b)给出了4种定位方法的目标位置估计均方根误差随着每个时隙段内样本点数的变化曲线;然后将信噪比设为-7 dB,每个时隙段内的样本点数设为100,目标位置设为(7,7) km,图5(c)给出了4种定位方法的目标位置估计均方根误差随着信号载波频率的变化曲线;最后将信噪比设为-7 dB,每个时隙段内的样本点数设为100,信号载波频率设为0.2 GHz,图5(d)给出了目标位置估计均方根误差随着目标在x轴方向坐标的变化曲线,这里假设目标在x轴方向上的坐标等于其在y轴方向上的坐标。

图5 目标位置估计均方根误差在x轴方向坐标的变化曲线(低信噪比条件)Fig.5 RMSE of source position estimation in x-axis (under low SNR condition)
从图5中可以看出:① 4种方法的定位精度均随着信噪比、样本点数以及信号载波频率的增加而提高,并且对近距离目标的定位精度要高于对远距离目标的定位精度;② 相比传统的DD方法,3种DPD方法在低信噪比和小样本数条件下的优势是显著的,这一点在文献[14]中也已经得到验证;③ 在低信噪比条件下,文中DPD方法的定位精度要优于文献[14]中的方法1,并且比方法1具有更高的噪声阈值(即产生门限效应的噪声功率),这是因为方法1中并未利用信号时域波形信息,而本文的DPD方法则融合了信号的恒模特征,从而提高了低信噪比条件下的定位精度;④ 在低信噪比条件下,文中DPD方法的定位精度要略差于文献[14]中的方法2,这是因为方法2假设信号波形精确已知,这比恒模特性包含了更多的信息,因此其定位精度自然也会更高,但总体而言,两者的性能差异并不大,值得一提的是,精确的波形信息在实际应用场景中并不总能轻易获得,但恒模特征则相对较容易满足。
5 结 论
1) 本文提出了一种基于多普勒频率的恒模信号DPD方法,并推导了针对恒模信号的目标位置直接估计方差的CRB,从而为DPD方法的参数估计精度提供定量的理论参考。
2) 数值实验表明,新方法的统计性能可以渐近逼近相应的CRB,并且相比没有信号时域波形信息的条件,通过利用恒模信号的恒包络特征可以提高目标定位精度,尤其是在低信噪比和小样本数的环境中。
3) 本文提出的DPD方法仅能针对单信号进行定位,后续的工作还要将其推广至多信号定位的场景中。
[1] YANG K, AN J P, BU X Y, et al. Constrained total least-squares location algorithm using time-difference-of-arrival measurements[J]. IEEE Transactions on Vehicular Technology, 2010, 59(3): 1558-1562.
[2] YU H G, HUANG G M, GAO J, et al. An efficient constrained weighted least squares algorithm for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Wireless Communications, 2012, 11(1): 44-47.
[3] HO K C, SUN M. Passive source localization using time differences of arrival and gain ratios of arrival[J]. IEEE Transactions on Signal Processing, 2008, 56(2): 464-477.
[4] KUTLUYIL D. Bearings-only target localization using total least squares[J]. Signal Processing, 2005, 85(9): 1695-1710.
[5] CHEUNG K W, SO H C, MA W K, et al. Least squares algorithms for time-of-arrival-based mobile location[J]. IEEE Transactions on Signal Processing, 2004, 52(4): 1121-1128.
[6] MASON J. Algebraic two-satellite TOA/FOA position solution on an ellipsoidal earth[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(7): 1087-1092.
[7] RAHMAN M Z, KLEEMAN L. Paired measurement localization: A robust approach for wireless localization[J]. IEEE Transactions on Mobile Computing, 2009, 8(8): 1087-1102.
[8] HO K C, CHAN Y T. An asymptotically unbiased estimator for bearings-only and Doppler-bearing target motion analysis[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 809-822.
[9] YANG L, SUN M, HO K C. Doppler-bearing tracking in the presence of observer location error[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 4082-4087.
[10] WEISS A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5): 513-516.
[11] WEISS A J, AMAR A. Direct position determination of multiple radio signals[J]. EURASIP Journal on Applied Signal Processing, 2005(1): 37-49.
[12] AMAR A, WEISS A J. Direct position determination in the presence of model errors—Known waveforms[J]. Digital Signal Processing, 2006, 16(1): 52-83.
[13] AMAR A, WEISS A J. A decoupled algorithm for geolocation of multiple emitters[J]. Signal Processing, 2007, 87(10): 2348-2359.
[14] AMAR A, WEISS A J. Localization of narrowband radio emitters based on Doppler frequency shifts[J]. IEEE Transactions on Signal Processing, 2008, 56(11): 5500-5508.
[15] SHALOM B O, WEISS A J. Direct position determination using MIMO radar[C]//Proceedings of the IEEE 25th Convention of Electrical and Electronics Engineers. Piscataway, NJ: IEEE Press, 2008: 575-579.
[16] SHALOM B O, WEISS A J. Efficient direct position determination of orthogonal frequency division multiplexing signals[J]. IET Radar, Sonar and Navigation, 2009, 3(2): 101-111.
[17] REUVEN A M, WEISS A J. Direct position determination of cyclostationary signals[J]. Signal Processing, 2009, 89(12): 2448-2464.
[18] OISPUU M, NICKEL U. Direct detection and position determination of multiple sources with intermittent emission[J]. Signal Processing, 2010, 90(12): 3056-3064.
[19] WEISS A J. Direct geolocation of wideband emitters based on delay and Doppler[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2513-5520.
[20] 张敏, 郭福成, 周一宇. 基于单个长基线干涉仪的运动单站直接定位[J]. 航空学报, 2013, 34(2): 378-386.
ZHANG M, GUO F C, ZHOU Y Y. A single moving observer direct position determination method using a long baseline interferometer[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 378-386 (in Chinese).
[21] 张敏, 郭福成, 周一宇, 等. 运动单站干涉仪相位差直接定位方法[J]. 航空学报, 2013, 34(9): 2185-2193.
ZHANG M, GUO F C, ZHOU Y Y, et al. A single moving observer direct position determination method using interferometer phase difference[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2185-2193 (in Chinese).
[22] POURHOMAYOUN M, FOWLER M L. Distributed computation for direct position determination emitter location[J]. IEEE Transactions on Aerospace and Electronic Sustems, 2014, 50(4): 2878-2889.
[23] LI J Z, YANG L, GUO F C, et al. Coherent summation of multiple short-time signals for direct positioning of a wideband source based on delay and Doppler[J]. Digital Signal Processing, 2016, 48(1): 58-70.
[24] TIRER T, WEISS A J. High resolution direct position determination of radio frequency sources[J]. IEEE Signal Processing Letters, 2016, 23(2): 192-196.
[25] TZAFRI L, WEISS A J. High-resolution direct position determination using MVDR[J]. IEEE Transactions on Wireless Communications, 2016, 15(9): 6449-6461.
[26] 王鼎, 张刚, 沈彩耀, 等. 一种针对恒模信号的运动单站直接定位算法[J]. 航空学报, 2016, 37(5): 1622-1633.
WANG D, ZHANG G, SHEN C Y, et al. A direct position determination algorithm for constant modulus signals with single moving observer[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1622-1633 (in Chinese).
[27] VAN DER VEEN A, PAULRAJ A. An analytical constant modulus algorithm[J]. IEEE Transactions on Signal Processing, 1996, 44(5): 1136-1155.
[28] LESHEM A, VEEN A J. Direction-of-arrival estimation for constant modulus signals[J]. IEEE Transactions on Signal Processing, 1999, 47(11): 3125-3129.
[29] STOICA P, BESSON O. Maximum likelihood DOA estimation for constant-modulus signal[J]. Electronic Letter, 2000, 36(9): 849-851.
[30] SEE C M S. Method for array calibration in high-resolution sensor array processing[J]. IEE Proceedings on Radar, Sonar and Navigation, 1995, 142(3): 90-96.
[31] DING W. Improved active calibration algorithms in the presence of channel gain/phase uncertainties and sensor mutual coupling effects[J]. Circuits, Systems, and Signal Processing, 2015, 34(6): 1825-1868.
[32] FRIEDLANDER B, WEISS A J. Direction finding in the presence of mutual coupling[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(3): 273-284.
[33] STOICA P, LARSSON E G. Comments on “Linearization method for finding Cramér-Rao bounds in signal processing”[J]. IEEE Transactions on Signal Processing, 2001, 49(12): 3168-3169.
[34] PESAVENTO M, GERSHMAN A B, WONG K M. Direction finding in partly-calibrated sensor arrays composed of multiple subarrays[J]. IEEE Transactions on Signal Processing, 2002, 55(9): 2103-2115.
附录A:


(A1)
于是函数h(z)的梯度向量和Hessian矩阵分别等于

(A2)
(A3)

(A4)
将式(A4)代入式(A2)中可知式(9)中的第1式成立。将式(A4)两边对向量z求导可知
(A5)
由式(A5)可以进一步推得

(A6)
将式(A4)和式(A6)代入式(A3)中可知式(9)中的第2式成立。至此,命题1得证。
(责任编辑: 苏磊)
*Corresponding author. E-mail: Cindyin0807@163.com
Direct localization method for constant modulus source based on Doppler frequency shifts
WANG Ding1,2, YIN Jiexin1,2,*, WU Zhidong1, LIU Ruirui1
1.SchoolofInformationSystemsEngineering,PLAInformationEngineeringUniversity,Zhengzhou450001,China2.NationalDigitalSwitchingSystemEngineering&TechnologicalResearchCenter,Zhengzhou450002,China
Compared with the conventional Differential Doppler (DD) localization method, the Direct Position Determination (DPD) method proposed by Amar and Weiss has higher position estimation accuracy under the condition of low Signal-to-Noise Ratio (SNR) and small number of samples. Based on this novel localization mechanism, a new DPD method using Doppler frequency shifts is presented for the constant modulus source. The DPD optimization model is constructed based on the Maximum Likelihood (ML) criterion as well as the constant modulus property of the source. All the unknowns are then classified into two groups according to the algebraic characteristic of the cost function, and an effective alternating iteration algorithm is presented to solve this DPD optimization problem numerically. In the proposed algorithm, two Newton-type iterative steps are devised for the two groups of unknowns, and then the grid search can be avoided and the multidimensional parameters are decoupled. The Cramér-Rao Bound (CRB) on the direct position estimation variance for constant modulus source is derived. Simulation results corroborate the good performance of the proposed method.
passive location; direct position determination; Doppler frequency; constant modulus source; maximum likelihood estimation; Newton-type iteration; Cramér-Rao bound
2016-12-30; Revised: 2017-02-08; Accepted: 2017-03-15; Published online: 2017-04-01 13:27
URL: www.cnki.net/kcms/detail/11.1929.V.20170401.1327.004.html
s: National Natural Science Foundation of China (61201381); China Postdoctoral Science Foundation (2016M592989); The Outstanding Youth Foundation of Information Engineering University (2016603201)
V324.2+3; TN911.7
A
1000-6893(2017)09-321084-14
2016-12-30; 退修日期: 2017-02-08; 录用日期: 2017-03-15; 网络出版时间: 2017-04-01 13:27
www.cnki.net/kcms/detail/11.1929.V.20170401.1327.004.html
国家自然科学基金(61201381); 中国博士后科学基金(2016M592989); 信息工程大学优秀青年基金(2016603201)
*通讯作者.E-mail: Cindyin0807@163.com
王鼎, 尹洁昕, 吴志东, 等. 一种基于多普勒频率的恒模信号直接定位方法[J]. 航空学报, 2017, 38(9): 321084. WANG D, YIN J X, WU Z D, et al. Direct localization method for constant modulus source based on Doppler frequency shifts[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 321084.
http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn
10.7527/S1000-6893.2017.321084
