基于贝叶斯理论的低循环疲劳寿命模型不确定性量化
2017-11-20王荣桥刘飞胡殿印李达
王荣桥, 刘飞, 胡殿印,*, 李达
1.北京航空航天大学 能源与动力工程学院, 北京 100083 2.先进航空发动机协同创新中心, 北京 100083 3.航空发动机结构强度北京市重点实验室, 北京 100083
基于贝叶斯理论的低循环疲劳寿命模型不确定性量化
王荣桥1,2,3, 刘飞1, 胡殿印1,2,3,*, 李达1
1.北京航空航天大学 能源与动力工程学院, 北京 100083 2.先进航空发动机协同创新中心, 北京 100083 3.航空发动机结构强度北京市重点实验室, 北京 100083
为量化低循环疲劳寿命模型中的不确定性因素,利用贝叶斯理论,采用经典的模型校准形式确立了寿命模型的不确定性量化形式,并结合正态性检验对误差项进行验证;应用马尔可夫链-蒙特卡罗(MCMC)算法获得了模型参数后验分布的抽样样本,在小子样试验数据条件下确定了低循环疲劳寿命的95%不确定性区间,较好地覆盖了寿命的分散性;对参数样本进行了相关性分析,并将异方差回归概率模型与贝叶斯概率模型进行了比较。最后,利用Morris全局灵敏度分析方法获得了Manson-Coffin模型参数的全局灵敏度指标;同时,验证了在模型参数对先验信息敏感,或者说在先验信息影响极大的情况下,采用无信息先验处理方法的合理性。
贝叶斯理论; 不确定性量化; 低循环疲劳; 概率模型; 全局灵敏度
涡轮盘作为航空发动机的关键限寿件,长期处于高温、高转速的工作环境,易引起低循环疲劳失效。涡轮盘结构的低循环疲劳在寿命表现上存在很大分散性,原因在于载荷、尺寸误差等外在随机因素带来的不确定性,以及材料组织不均匀、内部缺陷随机分布造成的结构寿命的固有分散属性[1]。此外,针对疲劳问题建立寿命预测模型时,存在物理建模不准确导致的认知不确定性问题。分散性问题和物理建模不准确问题可分别归结为寿命模型的模型参数不确定性和模型不确定性问题。因此,开展低循环疲劳寿命模型的不确定性量化研究,是进行涡轮盘结构设计的关键环节。
低循环疲劳寿命的分散性常用概率模型来量化,并且采用结构可靠性求解方法预估在指定置信度水平下的概率寿命[2-3]。目前,国内外学者已经提出了多种低循环疲劳寿命概率模型[4-7]。这些模型大多引入假设特定分布特征的随机变量,含有一定程度的主观性,从而造成预测寿命与实际寿命存在偏差。同时,由于试验周期长、费用高等原因,低循环疲劳试验获得的样本数据量偏少,从而导致基于概率统计理论的疲劳寿命概率模型预测可信度不高。
贝叶斯(Bayes)理论结合了先验信息,利用专家信息和已有试验数据作为问题的信息补充,适于处理小样本问题[8];另一方面,贝叶斯理论可以有效地确定模型参数的后验分布,克服假设参数分布特征的缺点。为此,本文选取基于Manson-Coffin形式的低循环疲劳寿命模型,依据量化模型不确定性的校准公式,并结合Bayes理论和马尔可夫链-蒙特卡罗(Markov Chain-Monte Carlo, MCMC)算法获得模型参数的联合后验分布,从而量化模型参数的不确定性。最后,开展了模型参数的灵敏度分析以确定主要影响因素。
1 模型不确定性量化的校准形式
模型校准是为了调整模型中的参数,从而保证模型预测与试验数据的一致性[9]。模型校准公式将物理模型和真实系统输出联系起来,考虑到观测误差、模型不确定性、剩余不确定性(完全相同输入条件下,物理过程有差异性结果)等不确定性因素,通过进一步的数学处理以获得准确的预测结果。
模型参数可分为2类:① 可控输入参数X,作为物理过程的状态参量,通常是已知的;② 校准输入参数θ,描述了模型应用的特定情境[10]。模型校准的一般形式[11]为
Ye=F(X,θ)+ε
(1)
式中:Ye为状态X时的测量值;F为模型函数;ε为误差项,综合包含了观测误差、剩余不确定性等因素,一般认为ε~N(0,ΣYe),ΣYe为观测误差间的协方差矩阵。
本文选取工程上常用的Manson-Coffin形式的低循环疲劳寿命模型,其表达式为[12]
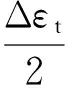
(2)
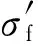
Manson-Coffin模型分为弹性和塑性2部分,相应地,可以将其分解为2个模型分别进行不确定性量化,即
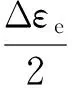
(3)
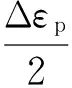
(4)
式中:εm1和εm2为模型误差项,表示试验测量值与模型输出的偏差。在概率模型建模及不确定性量化分析中,误差项及模型参数、疲劳寿命均视为随机变量。
已有研究表明[12],当误差水平εm1和εm2一定时,若应变水平降低,则低循环疲劳寿命的标准差以及变异系数会增大,即寿命的分散性将增大。从式(3)可以看出,在误差水平εm1一定的情况下,有

(5)
参数b<0,可见寿命Nf与变量Δεe/2-εm1满足负指数函数关系,具有单调递减下凹的性质,通过图解法和蒙特卡罗模拟方法,分析可知两者的变异系数具有正相关性。Δεe/2-εm1的变异系数表示为
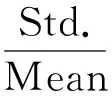
(6)
式中:Std.为标准差;Mean为均值;D(εm1)为方差。当应变水平Δεe减小,而误差εm1不变,那么Δεe/2-εm1变异系数增大,意味着寿命分散性也会增大。这说明采用的模型校准形式和误差项假设在定性上是合理的,而且也符合应变测量误差的物理意义。
本文的研究对象为涡轮盘典型材料GH720Li高温合金,试验应变比R=-1,温度为650 ℃,试验数据见文献[13]。首先对GH720Li合金低循环疲劳寿命模型校准式(1)中误差项的分布形式进行研究[14]。利用最小二乘法确定εm1和εm2的样本数据,利用Shapiro-Wilk(S -W)方法对其正态分布假设进行检验,结果见表1。

表1 误差项正态分布检验Table 1 Normal distribution test for error terms
样本量(样本自由度df)在3~2 000之间,εm1和εm2的正态性检验P值(显著性水平Sig)均大于检验水平0.05,说明εm1和εm2服从正态分布的假设是合理的。
2 模型参数不确定性的贝叶斯推理
在Bayes理论中,事件的观察者对于事件的初始认知被量化为概率的补充部分,通过不断地添加客观信息,实现对认知状态的更新。
根据Bayes公式,在数据D下模型参数θ的后验概率密度为
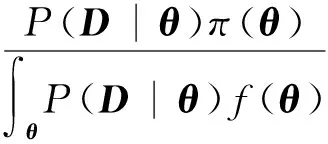
(7)
式中:π(θ)为模型参数θ的先验分布;P(D|θ)为似然函数。
根据模型评估式(1),若误差项满足ε~N(0,ΣYe),则参数校准的后验分布为
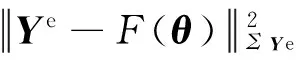
(8)
对于低循环疲劳寿命模型Manson-Coffin式(3)~式(4)参数校准的后验分布为
f(θm1|D)~
(9)
f(θm2|D)~
(10)
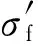
式(9)~式(10)的后验分布为非线性多元联合分布函数,采用MCMC算法进行抽样,利用蒙特卡罗方法在马尔可夫链平稳分布过程中抽样得到目标分布的样本。Metropolis-Hasting采样算法流程为[15]
1) 初始化马可尔夫链,选定初始点Xs0,确定预选分布q(Ys|Xs)。
2) 假设当前时刻为t,进行条件抽样,得到新的点yst,满足yst~q(Ys|Xst)。
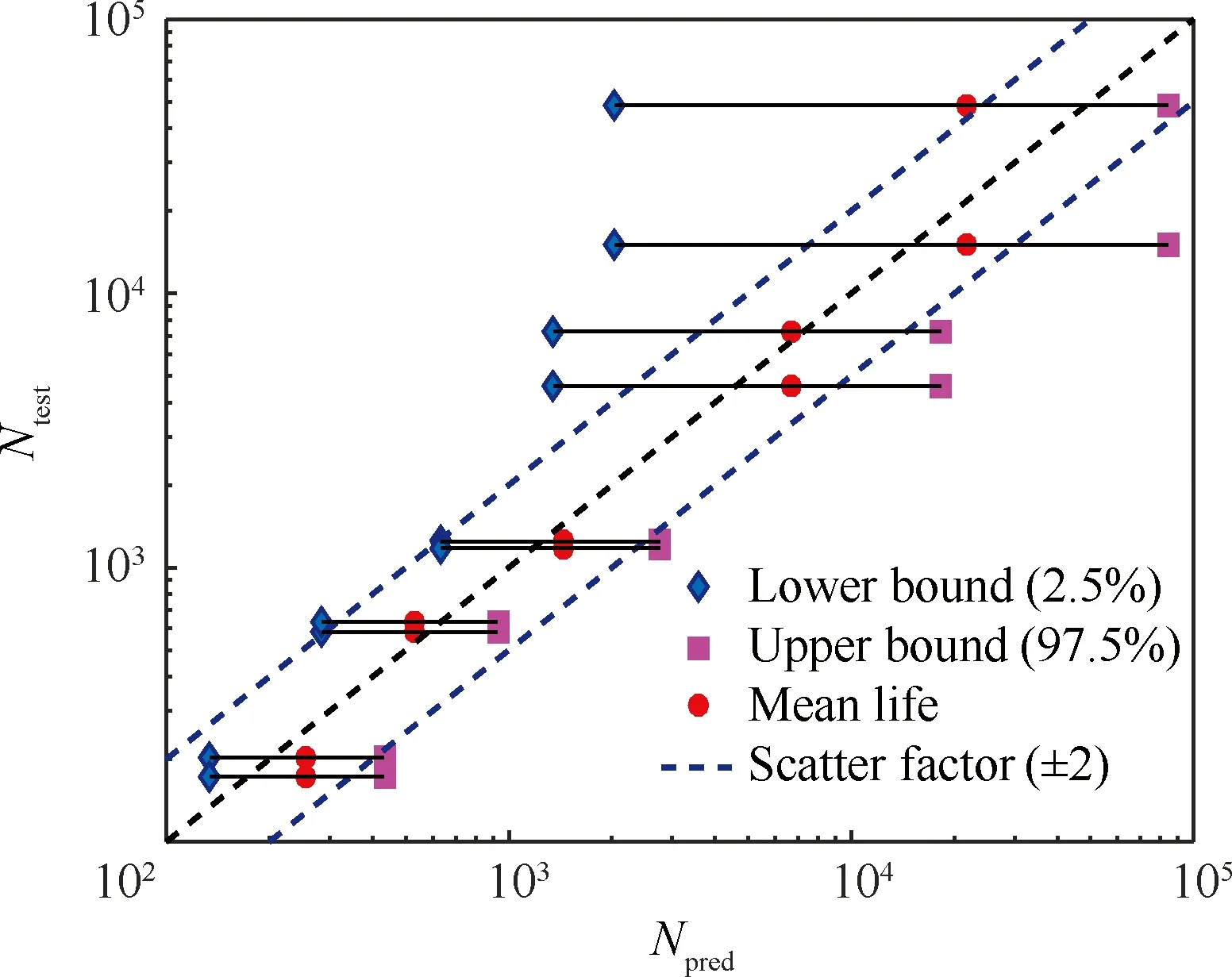
3) 从均匀分布采样u~U(0,1),若u 4) 转到2),继续抽样。 预选分布q(Ys|Xs)代表抽样过程中设计的马尔可夫过程,本文选取正态分布作为预选分布,通过马尔可夫链-蒙特卡罗算法得到了参数抽样样本。 模型参数的样本直接反映了其分布特性,可以通过核密度函数法拟合其概率密度函数,并对样本进行统计分析以量化模型参数的不确定性。 贝叶斯先验信息来源于经验、历史文献资料、积累的客观数据等。先验信息的选择是重要的,应该尽可能包括所有已知的关于参数的信息。在先验信息获取困难或者可信程度不高的情况下,应当采用无信息先验,对试验数据进行初步处理并作为先验信息的补充亦是一个可行的方法。 由专家经验及文献[16-17]得到GH720Li高温合金Manson-Coffin模型参数的先验信息见表2。 对式(9)~式(10)中参数的后验分布采用MCMC抽样方法获得其样本。其中,Manson-Coffin公式弹性部分的参数样本结果见图1和图2。 表2 Manson-Coffin模型中参数的先验分布 Table 2 Priority distribution of parameters in Manson-Coffin model ModelparameterProbabilitydistributionMeanStandarddeviationbGaussian-0.080.01σ'f/MPaGaussian131821.97E/GPaGaussian199.23.32cGaussian-0.550.05ε'fGaussian0.050.01 的抽样结果如图3和图4所示。 这样,得到的Manson-Coffin公式模型参数校准的统计结果如表3所示,97.5%和2.5%分别为上、下界。 图1 参数b抽样样本统计Fig.1 Sample statistics of parameter b 图2 参数/E抽样样本统计Fig.2 Sample statistics of parameter /E 图3 参数抽样样本统计Fig.3 Sample statistics of parameter 图4 参数c抽样样本统计Fig.4 Sample statistics of parameter c 表3 Manson-Coffin模型参数校准结果Table 3 Calibration of parameter in Manson-Coffin model ParameterMeanStandarddeviation2.5%97.5%b-0.08240.0023-0.0869-0.0780σ'f/E 0.00980.0001 0.0096 0.0101c-0.40100.0605-0.5269-0.2909ε'f 0.02410.0107 0.0104 0.0503 3.2.1 相关性来源及解释 C= (11) (12) 图5 参数与c的相关关系 Fig.5 Correlation relationship between parameter and c 3.2.2 “退化”模型 (13) 回归方法可以用更少的随机变量数量建立低循环疲劳寿命的概率模型。建立应变疲劳寿命概率模型的常用方法是同方差回归及异方差回归方法,见文献[12]和文献[18]。同方差回归是异方差回归的特殊情况。异方差回归方法考虑到寿命分散性随应力(应变)降低而增大的事实,能够更为准确地描述试验数据[19]。采用异方差回归方法处理Manson-Coffin模型,随机变量数量可以缩减到2个,结果如式(14)~式(15)所示。 (14) (15) 异方差回归方法与本文的贝叶斯方法是建立概率模型的2种不同的体系,各有优缺点。异方差回归方法中,模型参数可以用数量更少的随机变量μ1和μ2解析表示出来,这是贝叶斯方法做不到的。另一方面,根据式(14)~式(15)消去μ1和μ2,可得 (16) GH720Li高温合金的低循环疲劳寿命确定性模型为 (2Nf)-0.487 4 (17) 确定性模型中的参数值与表2和表3中的数据均相差较大。确定性模型采用最小二乘法,要求充分拟合试验数据,使得误差平方和最小。但表2数据属于先验信息,不依赖于试验数据,表3为后验信息,是先验信息和试验数据的综合,因此与确定性模型的数值偏差较大。另一个原因是,高维非线性最小二乘方法往往采用数值迭代算法求解,很难得到最优解,同时存在大量的局部最优解,式(17)中的参数值只是众多局部最优解中的一组。 确定性模型预测寿命分散带如图6所示,图中:Npred为预测寿命;Ntest为试验寿命。图6中确定性模型的寿命分散带ΔN=2.38,如上文所说,确定性模型的求解方法是对试验数据的充分拟合,必然获得最小的寿命分散带。确定性模型适合于评价理论模型的优劣,但在工程应用上表达不确定性因素的能力有限,适用性降低。 可以看到,预测寿命的不确定区间大部分在2倍误差带以内,预测均值的最大分散带为ΔN=2.697,说明低循环疲劳寿命模型的不确定性量化结果与试验数据吻合良好。预测寿命不确定性区间较好地覆盖了试验寿命,仅有一个试验数据的预测结果在2倍分散带以外,一方面原因在于低应力条件下试验寿命的分散性偏大,而且在中高周疲劳寿命的预测中,Manson-Coffin模型的适用性降低;另一方面,不确定区间随寿命增加呈增大趋势,但是在低应力高寿命范围下的不确定区间不足以表达寿命的真实分散性,不确定性量化方法仍然有改进的空间。 图6 确定性Manson-Coffin模型疲劳寿命预测 Fig.6 Fatigue life prediction based on deterministic Manson-Coffin model 图7 疲劳寿命模型预测的不确定性区间 Fig.7 Uncertainty intervals of fatigue life prediction model (18) 采用异方差回归处理疲劳试验数据,根据式(16)得到的参数样本结果为 (19) 由式(19),异方差回归导出的概率模型满足Manson-Coffin模型对数线性化的特点;对比式(12)和式(18),塑性部分参数样本的斜率为正,存在矛盾,说明采用异方差回归方法建立概率模型是有问题的。图8中,直线簇为将式(12)取对数后代入试验数据画出的,异方差回归参数样本明显超出直线簇的包络区域,区域外的点为异常样本。 经过同样的计算流程,采用异方差回归的低循环疲劳寿命概率模型得到的不确定性量化结果,如图9所示。 对比图7与图9可见,异方差回归方法预测的不确定性区间长度普遍增加,在低寿命区基本覆盖2倍寿命分散带,不确定性区间应用价值降低;随着应力水平降低,不确定性区间长度呈现快速发散状态,说明异方差回归方法建立的概率模型具有非正常的不稳定特点,主要原因在于塑性部分参数样本斜率为正,与Manson-Coffin公式的物理模型产生矛盾,从而导致样本异常。 图8 参数的原始样本和“退化”样本Fig.8 Original and degraded samples of parameters 图9 退化疲劳寿命模型预测的不确定性区间 Fig.9 Uncertainty intervals of degraded fatigue life model prediction 灵敏度分析是确定模型参数的不确定性对模型输出不确定性影响大小的一种分析方法,是模型参数校准过程中的重要工具[20]。全局灵敏度分析在输出参数的所有范围内,衡量模型输出对参数的灵敏度指标[21]。其中,Morris方法由于计算量小、易于操作,得到广泛应用。 Morris方法采用OAT(One factor at A Time)方式确定各个参数的基础效应,并进行基础效应的统计分析。用均值衡量参数对输出变量(如寿命)的灵敏度指标,以方差衡量各参数之间的相互作用。参数θi的一个基础效应计算式为 (20) 各参数θi的量纲不同时,应采用相对灵敏度分析[22],此时基础效应计算公式为 (21) 式中:Δ为θi的微小变化量。 图10 不同应变下各参数灵敏度指标Fig.10 Sensitivity index of parameters with different strains 1) 贝叶斯理论相比于传统概率方法,具有先验信息优势,可以利用历史数据(包括试验数据)和专家经验作为信息补充。在试验数据不易获得(小样本)的情况下,可得到较为准确的结果。 2) 将量化模型不确定性的校准公式应用到贝叶斯理论框架中,利用马尔可夫链-蒙特卡罗方法对模型参数后验分布进行抽样,从而得到模型参数的不确定性量化结果。 3) 在GH720Li高温合金低循环疲劳寿命模型的不确定性量化分析中,95%不确定性区间可以很好地表达试验寿命的分散性;通过对比发现,异方差回归概率模型存在不合理性。 4) 参数的全局灵敏度分析结果表明,寿命模型塑性部分的参数灵敏度相对较小,并且与应力水平正相关。 [1] 胡殿印, 裴月, 王荣桥, 等. 涡轮盘结构概率设计体系的研究[J]. 航空学报, 2008, 29(5): 1144-1149. HU D Y, PEI Y, WANG R Q, et al. Research of probabilistic design system for turbine disk structure[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1144-1149 (in Chinese). [2] 胡殿印, 裴月, 王荣桥, 等. 涡轮盘低循环疲劳的概率设计[J]. 推进技术, 2008, 29(4): 481-487. HU D Y, PEI Y, WANG R Q, et al. Probability design of low cycle fatigue for turbine disk[J]. Journal of Propulsion Technology, 2008, 29(4): 481-487 (in Chinese). [3] 汤咏. 基于不确定性的航空发动机涡轮盘概率疲劳寿命预测模型[D]. 成都: 电子科技大学, 2013: 4-5. TANG Y. Fatigue life prediction model of aeroengine turbine disk based on uncertainty[D]. Chengdu: University of Electronic Science and Technology, 2013: 4-5 (in Chinese). [4] BALDWIN J D, THACKER J G. A strain-based fatigue reliability analysis method[J]. Journal of Mechanical Design, 1995, 117(2): 229-234. [5] ZHAO J, TANG J, WU H C. A reliability assessment method in strain-based fatigue life analysis[J]. Journal of Pressure Vessel Technology, 1998, 120(1): 99-104. [6] 唐俊星, 陆山. 某涡轮盘低循环疲劳概率寿命数值模拟[J]. 航空动力学报, 2006, 21(4): 706-710. TANG J X, LU S. Numerical simulation of low cycle fatigue life of a turbine disk[J]. Journal of Aerospace Power, 2006, 21(4): 706-710 (in Chinese). [7] BARGMANN H, RÜSTENBERG I, DEVLUKIA J. Reliability of metal components in fatigue: A simple algorithm for the exact solution[J]. Fatigue & Fracture of Engineering Materials & Structures, 1994, 17(12): 1445-1457. [8] 朱顺鹏, 黄洪钟, 甘露萍, 等. 基于模型不确定性量化的涡轮盘结构概率寿命预测[C]//中国运筹学会可靠性分会可靠性学术会议. 北京: 中国运筹学会, 2013: 261-269. ZHU S P, HUANG H Z, GAN L P, et al. Probabilistic life prediction for aircraft turbine disk based on model uncertainty quantification[C]//Reliability Academic Conference of the Reliability Branch of China Operational Research Society. Beijing: China Operational Research Society, 2013: 261-269 (in Chinese). [9] ACEBAL R. Guide for the verification and validation of computational fluid dynamics simulation: AIAA-1998-0077[R]. Reston, VA: AIAA, 1998. [10] KENNEDY M C, O’HAGAN A. Bayesian calibration of computer models[J]. Journal of the Royal Statistical Society Series B—Statistical Methodology, 2001, 63(3): 425-464. [11] ANGEL U, SANKARAN M, THOMAS L P. Quanlification of margins and uncertainties of complex systems in the presence of aleatoric and epistemic uncertainty[J]. Realibity Engineering and System Safety, 2011, 96(9): 1114-1125. [12] 高阳, 白广忱, 张瑛莉. 涡轮盘低循环疲劳寿命的概率分析[J]. 航空动力学报, 2009, 24(4): 804-809. GAO Y, BAI G C, ZHANG Y L. Probability analysis for the low cycle fatigue life of a turbine disk[J]. Journal of Aerospace Power, 2009, 24(4): 804-809 (in Chinese). [13] 中国金属学会高温材料分会. 中国高温合金手册[M]. 北京: 中国质检出版社, 2012: 870-874. High Temperature Materials Branch of Chinese Society of Metals. China high temperature alloy handbook[M]. Beijing: China Zhijian Publishing House, 2012: 870-874 (in Chinese). [14] SHANKAR S. Uncertainty qualification in fatigue damage prognosis[C]//Annual Conference of the Prognostics and Health Management Society, 2009: 1-13. [15] CHAO M A, MATHÉ P, SCHLOßHAUER V, et al. Calibration and uncertainty quantification of gas turbines performance models: GT 2015-42392[R]. New York: ASME, 2015. [16] 姚伟, 白广忱. 基于Fourier正交基神经网络的涡轮盘低循环疲劳可靠性分析[J]. 装备制造技术, 2014(10): 132-134. YAO W, BAI G C. Reliability analysis of low cycle fatigue of turbine disk based on Fourier orthogonal neural network[J]. Equipment Manufacturing Technology, 2014(10): 132-134 (in Chinese). [17] 高阳, 白广忱, 陈冲. 基于RBF神经网络的涡轮盘疲劳可靠性分析[J]. 机械设计, 2009, 26(5): 8-14. GAO Y, BAI G C, CHEN C. Fatigue reliability analysis of turbine disk based on RBF neural network[J]. Journal of Machine Design, 2009, 26(5): 8-14 (in Chinese). [18] 唐俊星, 陆山. 轮盘应变疲劳寿命可靠性分析方法[J]. 推进技术, 2005, 26(4): 344-347. TANG J X, LU S. Reliability analysis method for the strain fatigue life of a disk[J]. Journal of Propulsion Technology, 2005, 26(4): 344-347 (in Chinese). [19] 傅惠民. 线性异方差回归分析[J]. 航空学报, 1994, 15(3): 295-302. FU H M. Linear variance regression analysis[J]. Acta Aeronautica et Astronautica Sinica, 1994, 15(3): 295-302 (in Chinese). [20] GARNER R H, O’NEILL R V, MANKIN J B. A comparison of sensitivity and error analysis based on a stream ecosystem model[J]. Ecological Modelling, 1981, 12(3): 173-190. [21] 孙艳伟, 把多铎, 王文川, 等. SWMM模型径流参数全局灵敏度分析[J]. 农业机械学报, 2012, 43(7): 43-49. SUN Y W, BA D D, WANG W C, et al. Global sensitivity analysis of runoff parameters of SWMM model[J]. Chinese Journal of Agricultural Machinery, 2012, 43(7): 43-49 (in Chinese). [22] 钱文学, 尹晓伟, 何雪浤, 等. 压气机轮盘疲劳寿命影响参量的灵敏度分析[J]. 东北大学学报:自然科学版, 2006, 27(6): 677-680. QIAN W X, YIN X W, HE X H, et al. Sensitivity analysis of influential parameter on the fatigue life of compressor disk[J]. Journal of Northeastern University: Natural Science, 2006, 27(6): 677-680 (in Chinese). (责任编辑: 张晗) *Corresponding author. E-mail: hdy@buaa.edu.cn Uncertainty quantification in low cycle fatigue life model based on Bayesian theory WANG Rongqiao1,2,3, LIU Fei1, HU Dianyin1,2,3,*, LI Da1 1.SchoolofEnergyandPowerEngineering,BeihangUniversity,Beijing100083,China2.CollaborativeInnovationCenterofAdvancedAero-Engine,Beijing100083,China3.BeijingKeyLaboratoryofAero-EngineStructureandStrength,Beijing100083,China To quantify the uncertainties in the model for low cycle fatigue life prediction, the classic model calibration method is applied using Bayesian theory, and the error term was verified by the normality test. Posterior distribution of the model parameter samples is obtained by Markov Chain-Monte Carlo (MCMC) simulation. An application is presented where a 95% interval of fatigue life prediction well describes the dispersity in real tests with small data samples. Correlation analysis of the samples of parameters is conducted to establish the heteroscedastic regression model. Comparison of the two models shows that the heteroscedastic regression model is questionable in uncertainty quantification performance. Morris global sensitivity analysis method is applied to quantify the sensitivity of the parameters in Manson-Coffin model, indicating that the non-informative prior is reasonable if posterior distribution is sensitive to the prior. Bayesian theory; uncertainty quantification; low cycle fatigue; probabilistic model; global sensitivity 2016-10-08; Revised: 2016-12-26; Accepted: 2017-05-31; Published online: 2017-06-02 16:55 URL: www.cnki.net/kcms/detail/11.1929.V.20170602.1655.002.html s: National Natural Science Foundation of China (51675024, 51305012, 51375031); Aeronautical Science Foundation of China (2014ZB51) V231.95; O346.2+3 A 1000-6893(2017)09-220832-10 2016-10-08; 2016-12-26; 录用日期: 2017-05-31; 网络出版时间: 2017-06-02 16:55 www.cnki.net/kcms/detail/11.1929.V.20170602.1655.002.html 国家自然科学基金(51675024, 51305012, 51375031); 航空科学基金(2014ZB51) *通讯作者.E-mail: hdy@buaa.edu.cn 王荣桥, 刘飞, 胡殿印, 等. 基于贝叶斯理论的低循环疲劳寿命模型不确定性量化[J]. 航空学报, 2017, 38(9): 220832. WANG R Q, LIU F, HU D Y, et al. Uncertainty quantification in low cycle fatigue life model based on Bayesian theory[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 220832. http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn 10.7527/S1000-6893.2017.2208323 GH720Li合金低循环疲劳寿命模型的不确定性量化
3.1 模型参数后验分布的抽样分析


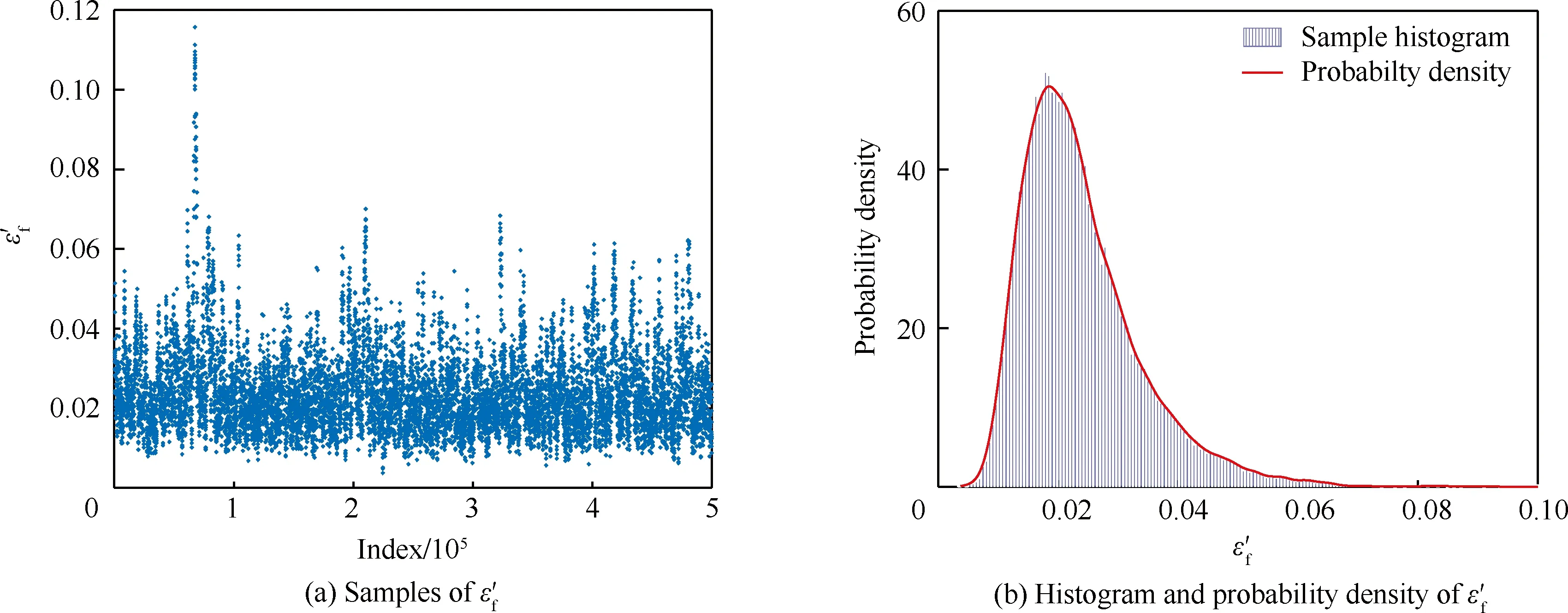
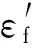
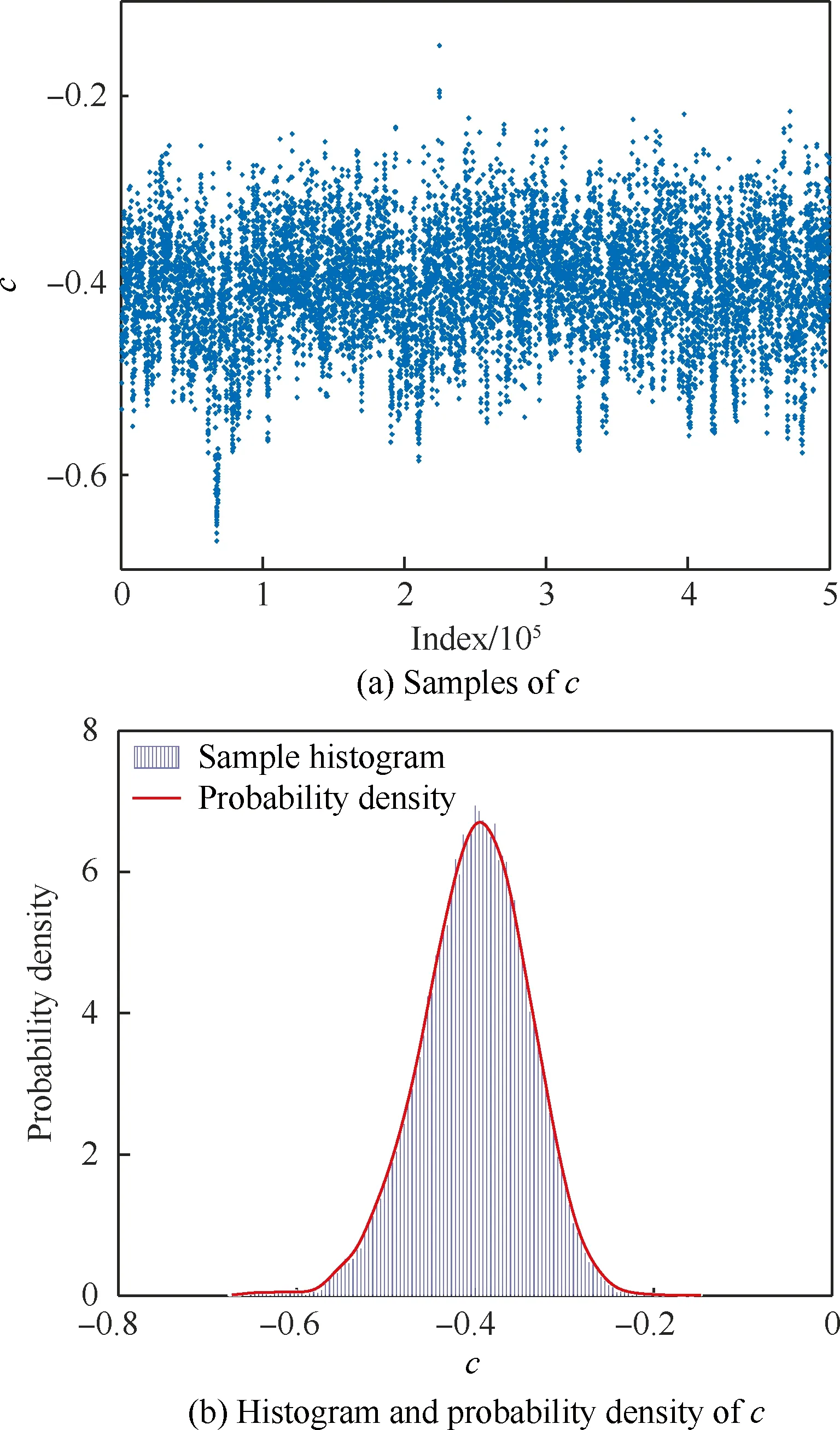
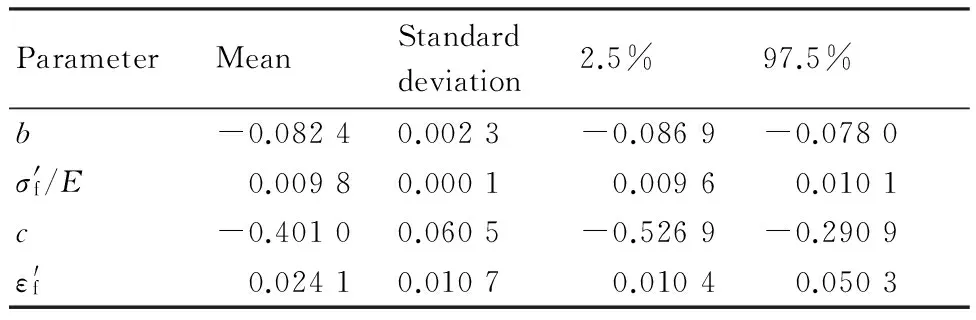
3.2 参数的相关性分析
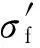

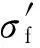

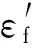

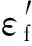
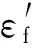

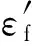

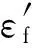
3.3 低循环疲劳寿命的不确定性量化
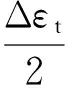
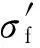
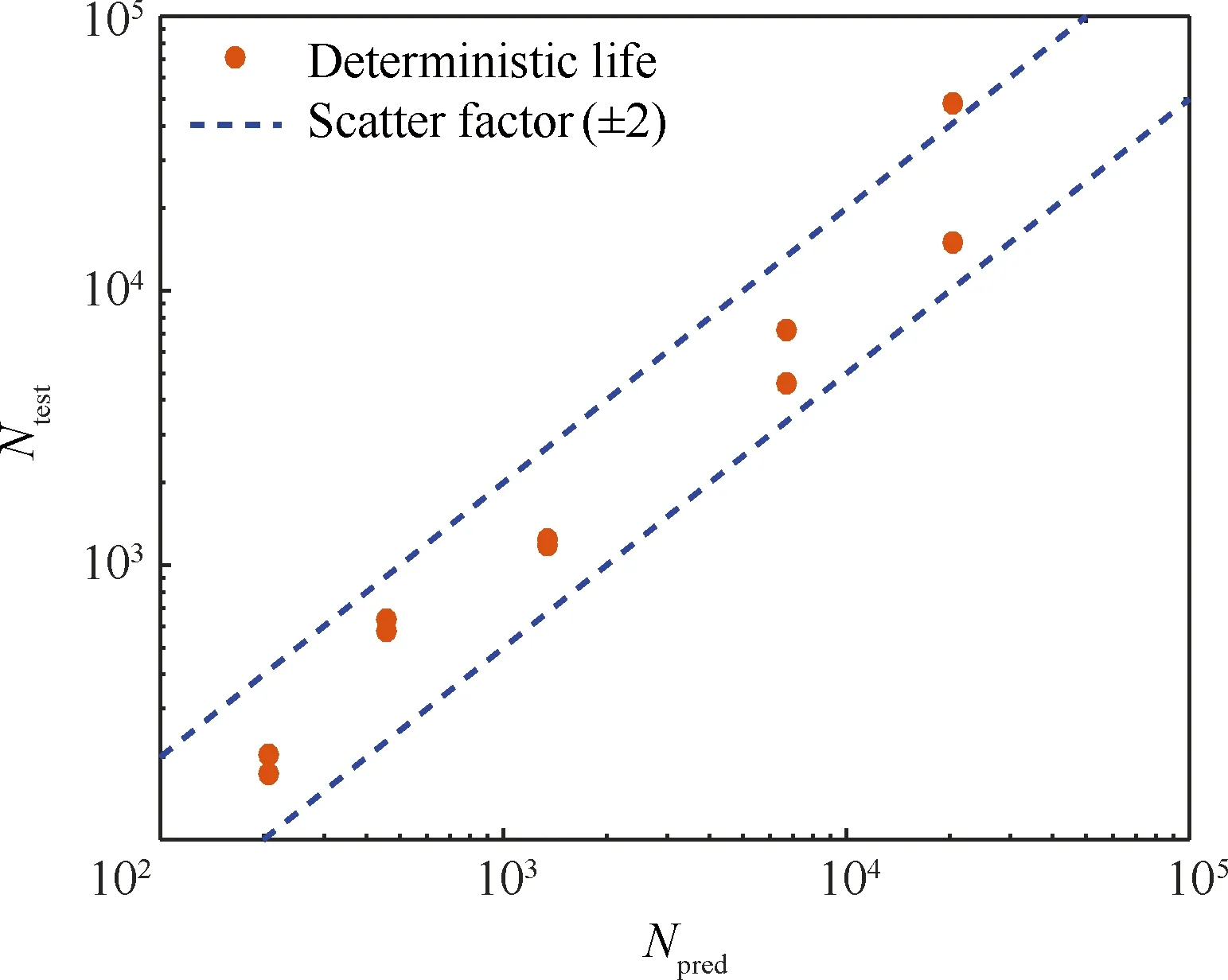

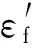

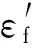
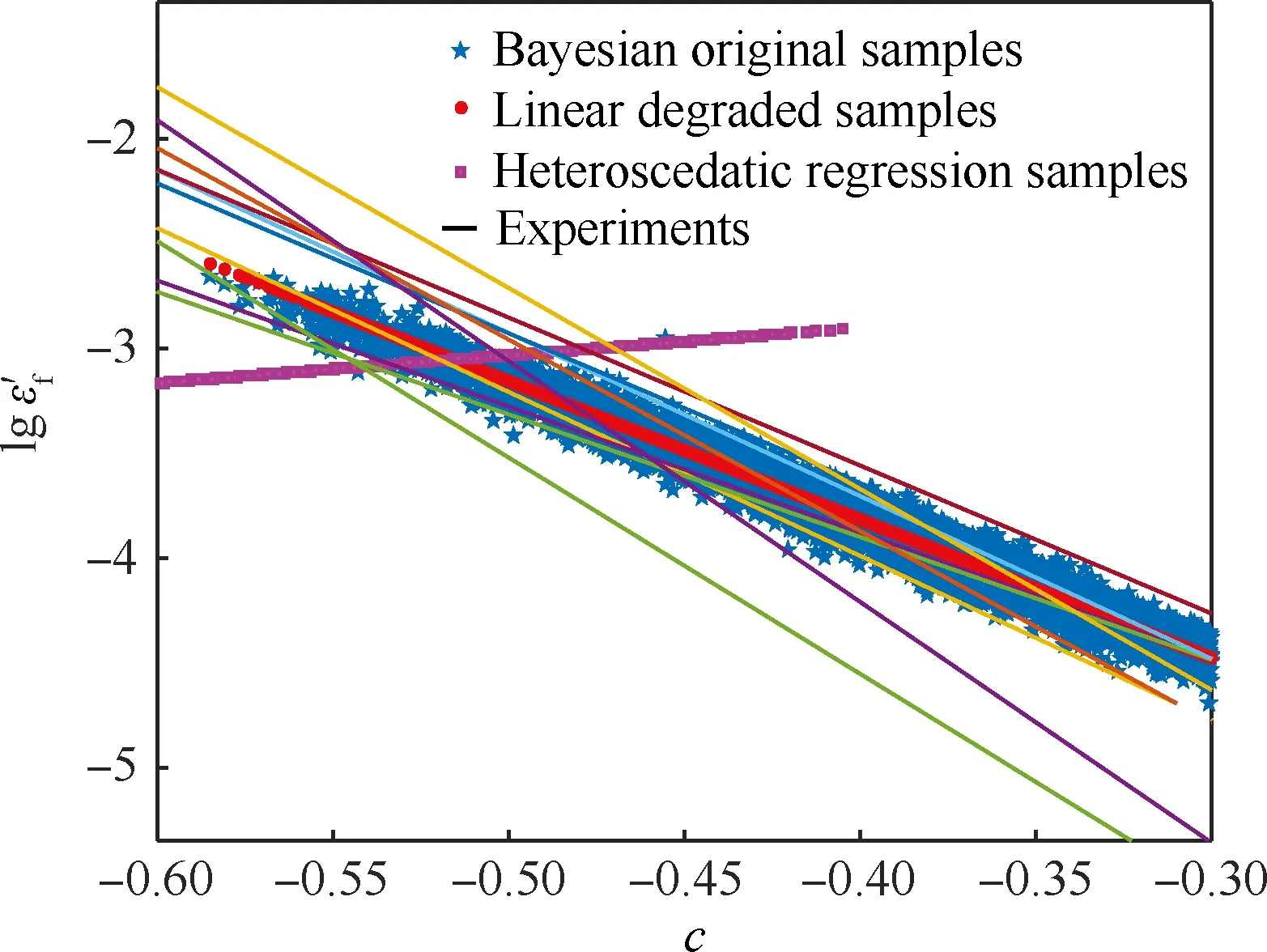
4 灵敏度分析

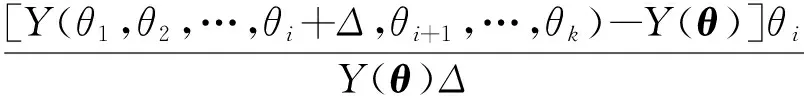
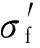

5 结 论
